C++版本的OpenCV实现二维图像的卷积定理(通过傅里叶变换实现二维图像的卷积过程,附代码!!)
C++版本的OpenCV库实现二维图像的卷积定理过程详解
- 前言
- 一、卷积定理简单介绍
- 二、不同卷积过程对应的傅里叶变换过程
- 1、“Same”卷积
- 2、“Full”卷积
- 3、“Valid”卷积
- 三、基于OpenCV库实现的二维图像卷积定理
- 四、基于FFTW库实现的二维图像卷积定理
- 五、总结与讨论
前言
工作中用到许多卷积过程,需要转成C++代码的实现,使用OpenCV库自带的二维卷积过程所耗费的时间比较久,为了提升代码的运行效率可以考虑使用卷积定理实现二维图像的卷积过程。
一、卷积定理简单介绍
卷积定理是傅立叶变换满足的一个重要性质。卷积定理指出,函数卷积的傅立叶变换是函数傅立叶变换的乘积。具体分为时域卷积定理和频域卷积定理,时域卷积定理即时域内的卷积对应频域内的乘积;频域卷积定理即频域内的卷积对应时域内的乘积,两者具有对偶关系。
二、不同卷积过程对应的傅里叶变换过程
1、“Same”卷积
假设原始图像的大小为mxm,卷积核的大小为nxn。此时进行same卷积,则卷积后生成的图像大小为mxm,此时进行卷积是需要对原始图像进行padding操作,需要对原始图像周围进行n-1个补零操作,此时被卷积图像大小padding为(m+n-1)x(m+n-1),然后进行卷积操作,进行傅里叶变化是需要先将被卷积图像以及卷积核的大小都padding为(m+n-1)x(m+n-1),因为要进行傅里叶变换后的乘积操作,因此被卷积图像以及卷积核的大小需要相等。经过卷积定理的操作之后,将生成的(m+n-1)x(m+n-1)大小的图像按照padding的逆操作进行裁剪,得到mxm的图像即为same卷积得到的卷积图像。
Python代码验证
import numpy as np
from scipy import signal# 原始图像 f(x)
gray = np.uint16(np.random.randint(100, size=(7, 7)))
# 卷积核 g(x)
kenel = np.ones((3, 3))/9
# ----- Conv = f(x)*g(x) ----- #
# f(x)*g(x)
Conv = signal.convolve2d(gray, kenel, mode='same') # 使用full卷积类型,得到(M+N-1)X(M+N-1)大小#--------- ifft{ F(f(x))·F(g(x)) } ---------#
# 傅里叶变换前进行 padding 填充,图像和卷积核都补零到 (M+N-1)x(M+N-1)大小。
img_pad = np.pad(gray, ((1, 1), (1, 1)), 'constant')
kenel_pad = np.pad(kenel, ((3, 3),(3, 3)), 'constant')# F(f(x))
img_fft = np.fft.fftshift(np.fft.fft2(img_pad))
# F(g(x))
kenel_fft = np.fft.fftshift(np.fft.fft2(kenel_pad))
# ifft( F(f(x))·F(g(x)) )
FFT = np.fft.ifftshift(np.fft.ifft2(np.fft.fftshift(img_fft*kenel_fft)))#--------- 打印结果 ---------#
print(" f(x) ↓")
print(gray)
print(" g(x) ↓")
print(kenel)print("\n\n f(x)*g(x) ↓")
print(np.uint8(Conv))
print("\n ifft[F·G] ↓")
print(np.uint8(np.abs(FFT)))
结果展示
上述代码的结果如下图所示,可见卷积定理得到的结果经过裁剪后的红框中的内容与same卷积得到的结果一致。

2、“Full”卷积
假设原始图像的大小为mxm,卷积核的大小为nxn。此时进行full卷积,则卷积后生成的图像大小为(m+n-1)x(m+n-1),此时进行卷积是需要对原始图像进行padding操作,需要对原始图像周围进行2n-2个补零操作,此时被卷积图像大小padding为(m+2n-2)x(m+2n-12),然后进行卷积操作,进行傅里叶变化是需要先将被卷积图像以及卷积核的大小都padding为(m+n-1)x(m+n-1),因为要进行傅里叶变换后的乘积操作,因此被卷积图像以及卷积核的大小需要相等。经过卷积定理的操作之后,得到(m+n-1)x(m+n-1)的图像即为full卷积得到的卷积图像。
Python代码验证
import numpy as np
from scipy import signal# 原始图像 f(x)
gray = np.uint16(np.random.randint(100, size=(9, 9)))
# 卷积核 g(x)
kenel = np.ones((5, 5))/9
# ----- Conv = f(x)*g(x) ----- #
# f(x)*g(x)
Conv = signal.convolve2d(gray, kenel, mode='full') # 使用full卷积类型,得到(M+N-1)X(M+N-1)大小#--------- ifft{ F(f(x))·F(g(x)) } ---------#
# 傅里叶变换前进行 padding 填充,图像和卷积核都补零到 (M+N-1)x(M+N-1)大小。
img_pad = np.pad(gray, ((2, 2), (2, 2)), 'constant')
kenel_pad = np.pad(kenel, ((4, 4), (4, 4)), 'constant')# F(f(x))
img_fft = np.fft.fftshift(np.fft.fft2(img_pad))
# F(g(x))
kenel_fft = np.fft.fftshift(np.fft.fft2(kenel_pad))
# ifft( F(f(x))·F(g(x)) )
FFT = np.fft.ifftshift(np.fft.ifft2(np.fft.fftshift(img_fft*kenel_fft)))#--------- 打印结果 ---------#
print(" f(x) ↓")
print(gray)
print(" g(x) ↓")
print(kenel)print("\n\n f(x)*g(x) ↓")
print(np.uint8(Conv))
print("\n ifft[F·G] ↓")
print(np.uint8(np.abs(FFT)))
结果展示
上述代码的结果如下图所示,可见卷积定理得到的结果与full卷积得到的结果一致。

3、“Valid”卷积
假设原始图像的大小为mxm,卷积核的大小为nxn。此时进行valid卷积,则卷积后生成的图像大小为(m-n+1)x(m-n+1),此时不需要对被卷积图像进行padding操作,直接进行卷积操作,进行傅里叶变化是需要先将卷积核的大小padding为mxm,因为要进行傅里叶变换后的乘积操作,因此被卷积图像以及卷积核的大小需要相等。经过卷积定理的操作之后,将生成的mxm的图像进行裁剪,得到(m-n+1)x(m-n+1)的图像即为valid卷积得到的卷积图像。
Python代码验证
import numpy as np
from scipy import signal# 原始图像 f(x)
gray = np.uint16(np.random.randint(100, size=(9, 9)))
# 卷积核 g(x)
kenel = np.ones((5, 5))/9
# ----- Conv = f(x)*g(x) ----- #
# f(x)*g(x)
Conv = signal.convolve2d(gray, kenel, mode='valid') # 使用full卷积类型,得到(M+N-1)X(M+N-1)大小#--------- ifft{ F(f(x))·F(g(x)) } ---------#
# 傅里叶变换前进行 padding 填充,图像和卷积核都补零到 (M+N-1)x(M+N-1)大小。
img_pad = np.pad(gray, ((0, 0), (0, 0)), 'constant')
kenel_pad = np.pad(kenel, ((2, 2), (2, 2)), 'constant')# F(f(x))
img_fft = np.fft.fftshift(np.fft.fft2(img_pad))
# F(g(x))
kenel_fft = np.fft.fftshift(np.fft.fft2(kenel_pad))
# ifft( F(f(x))·F(g(x)) )
FFT = np.fft.ifftshift(np.fft.ifft2(np.fft.fftshift(img_fft*kenel_fft)))#--------- 打印结果 ---------#
print(" f(x) ↓")
print(gray)
print(" g(x) ↓")
print(kenel)print("\n\n f(x)*g(x) ↓")
print(np.uint8(Conv))
print("\n ifft[F·G] ↓")
print(np.uint8(np.abs(FFT)))
结果展示
上述代码的结果如下图所示,可见卷积定理得到的结果经过裁剪后的红框中的内容与valid卷积得到的结果一致。

三、基于OpenCV库实现的二维图像卷积定理
//本代码实现的是使用193x193大小的卷积核对193x193大小的被卷积图像进行卷积操作
Conv2Kernel(kernelImage, inputImage, outputImage, n, n);
cv::Mat matPaded1;
cv::Mat matPaded2;
cv::Mat kernelPaded;
cv::Mat fftKernel;
cv::Mat fftMat1;
cv::Mat fftMat2;
cv::Mat result1;
cv::Mat result2;cv::copyMakeBorder(matKernel, kernelPaded, 192, 215, 192, 215, cv::BORDER_CONSTANT, cv::Scalar(0.f));
cv::copyMakeBorder(matConv1, matPaded1, 192, 215, 192, 215, cv::BORDER_CONSTANT, cv::Scalar(0.f));cv::Mat planes1[] = { cv::Mat_<float>(kernelPaded),cv::Mat::zeros(kernelPaded.size(),CV_32F)
};
cv::Mat planes2[] = { cv::Mat_<float>(matPaded1),cv::Mat::zeros(matPaded1.size(),CV_32F)
};
cv::merge(planes1, 2, fftKernel);
cv::merge(planes2, 2, fftMat1);cv::dft(fftKernel, fftKernel, cv::DFT_COMPLEX_OUTPUT);
cv::dft(fftMat1, fftMat1, cv::DFT_COMPLEX_OUTPUT);fftshift(fftKernel);
fftshift(fftMat1);
cv::Mat fftMultiplication1;
cv::mulSpectrums(fftKernel, fftMat1, fftMultiplication1, cv::DFT_ROWS);
cv::idft(fftMultiplication1, result1, cv::DFT_INVERSE + cv::DFT_SCALE + cv::DFT_COMPLEX_OUTPUT);ifftshift(result1);
cv::split(result1, planes1);
cv::magnitude(planes1[0], planes1[1], planes1[0]);cv::Mat matConv3 = planes1[0](cv::Rect(192, 192, 193, 193)).clone();
代码详解
1、对被卷积图像和卷积核执行padding操作
由于使用的是same卷积,按照上文same卷积的过程对其进行padding操作,图像上下左右四个方向都补上192个0。下述代码右边和下面之所以补零数不是192,是因为在进行傅里叶变换时,特定长度的矩阵速度更快,因此补了更多的0。但是我在实验过程中并没有发现速度有变快
2、对padding后的图像矩阵进行傅里叶变换
对padding后的卷积核以及被卷积图像执行傅里叶变换,然后进行fftshift操作。
3、对傅里叶变换后的图像矩阵进行点乘操作
4、对点乘后的举证进行傅里叶逆变换
对点乘后的矩阵执行傅里叶逆变换,然后进行ifftshift操作。
5、截取合适位置的图像,具体位置根据padding过程确定,得到的图像矩阵即为卷积后的图像矩阵。
四、基于FFTW库实现的二维图像卷积定理
fftw_complex* pImgOut = (fftw_complex*)fftw_malloc(sizeof(fftw_complex) * 600 * 600);fftw_plan pRef;pRef = fftw_plan_dft_2d(600, 600, pImgIn, pImgOut, FFTW_FORWARD, FFTW_ESTIMATE);fftw_execute(pRef);fftw_destroy_plan(pRef);fftw_free(pImgIn);fftw_free(pImgOut);
五、总结与讨论
经过不懈努力终于使用C++实现了卷积定理,想要进一步提升卷积过程的速度,优化代码性能。但是天不遂人愿,在我的任务中使用卷积定义实现卷积过程和使用OpenCV库中的卷积操作接口速度相差无几,几乎没有看到在计算速度上有提升,忙了半天白忙活了,难受~。分析原因可能是由于本次任务的卷积过程比较特殊,卷积核、被卷积图像的大小一致,导致进行padding操作时,padding后的图像几乎是原图像的9倍大小,造成傅里叶变换以及傅里叶逆变换的过程速度变慢,影响了整体流程的速度。
相关文章:

C++版本的OpenCV实现二维图像的卷积定理(通过傅里叶变换实现二维图像的卷积过程,附代码!!)
C版本的OpenCV库实现二维图像的卷积定理过程详解 前言一、卷积定理简单介绍二、不同卷积过程对应的傅里叶变换过程1、“Same”卷积2、“Full”卷积3、“Valid”卷积 三、基于OpenCV库实现的二维图像卷积定理四、基于FFTW库实现的二维图像卷积定理五、总结与讨论 前言 工作中用…...
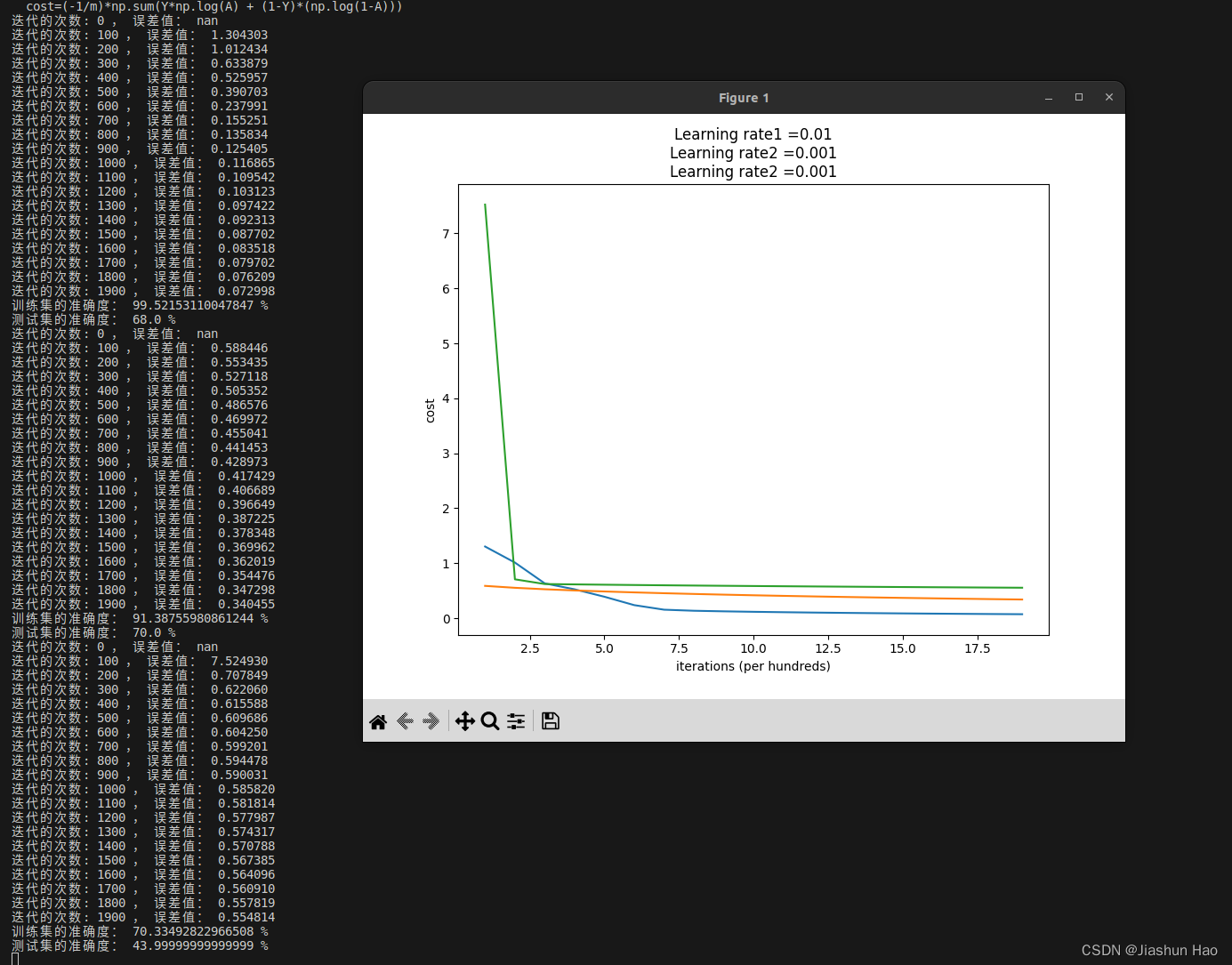
打开深度学习的锁:(1)入门神经网络
打开深度学习的锁 导言PS:神经网络的训练过程一、导入的包和说明二、数据的预处理2.1 数据集说明2.2 数据集降维度并且转置2.3 数据预处理完整代码 三、逻辑回归3.1 线性回归函数公式3.2 sigmoid函数公式 四、初始化函数五、构建逻辑回归的前向传播和后向传播5.1 损…...

02- pytorch 实现 RNN
一 导包 import torch from torch import nn from torch.nn import functional as F import dltools 1.1 导入训练数据 batch_size, num_steps 32, 35 # 更改了默认的文件下载方式,需要将 article 文件放入该文件夹 train_iter, vocab dltools.load_data_time_…...

算法课作业1
https://vjudge.net/contest/581138 A - Humidex 模拟题 题目大意 给三个类型数字通过公式来回转化 思路 求e的对数有log函数,不懂为什么不会出精度错误,很迷,给的三个数字也没有顺序,需要多判断。 #include<cstdio>…...

linux文本处理 两行变一行
linux简单文本处理 [rootkvm ~]# cat test 1.1.1.1 test1 2.2.2.2 test2 3.3.3.3 test3 192.168.1.2 test4 10.23.9.19 test5 cat test | awk /^[0-9]/{T$1;next;}{print T,$1}1.1.1.1 test1 2.2.2.2 test2 3.3.3.3 test3 192.168.1.2 test4 10.23.9.19 test5 cat test | …...

第二次面试 9.15
首先就是自我介绍 项目拷打 总体介绍一下项目 谈一下对socket的理解 在数据接收阶段,如何实现一个异步的数据处理 谈一谈对qt信号槽的理解 有想过如何去编写一个信号槽吗 你是如何使用CMAKE编译文件的 C11特性了解些啥 shared_ptr 和 unique_ptr 的运用场景 …...
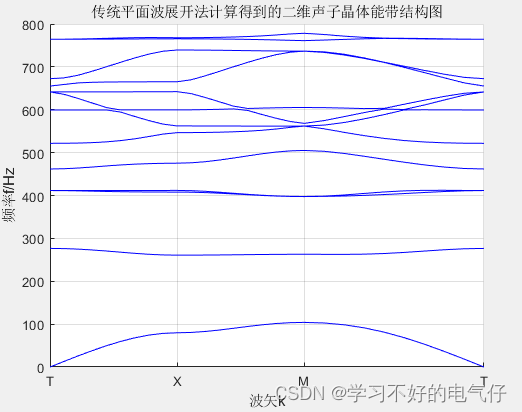
基于matlab实现的平面波展开法二维声子晶体能带计算程序
Matlab 平面波展开法计算二维声子晶体二维声子晶体带结构计算,材料是铅柱在橡胶基体中周期排列,格子为正方形。采用PWE方法计算 完整程序: %%%%%%%%%%%%%%%%%%%%%%%%% clear;clc;tic;epssys1.0e-6; %设定一个最小量,避免系统截断误差或除零错…...
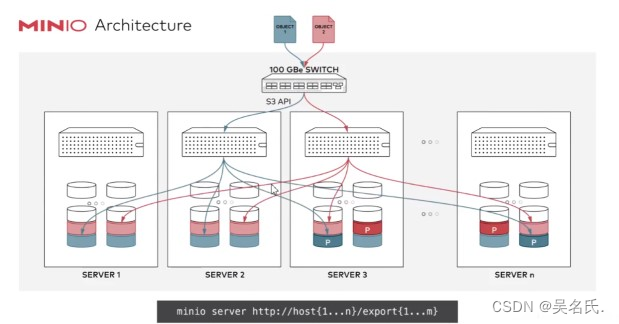
Minio入门系列【2】纠删码
1 纠删码 Minio使用纠删码erasure code和校验和checksum来保护数据免受硬件故障和无声数据损坏。 即便丢失一半数量(N/2)的硬盘,仍然可以恢复数据 1.1 什么叫纠删码 纠删码是一种用于重建丢失或损坏数据的数学算法。 纠删码(e…...
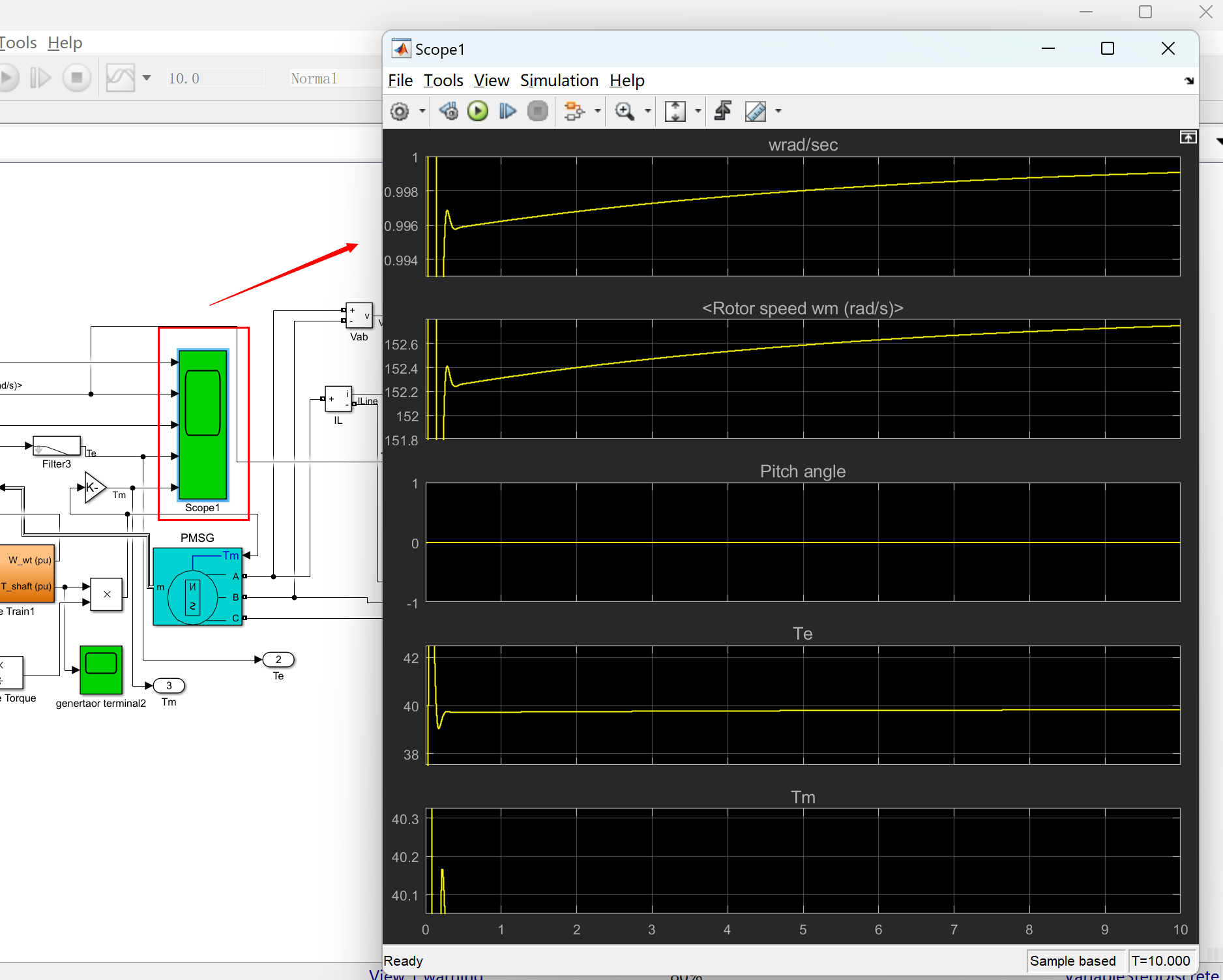
基于永磁同步发电机的风力发电系统研究(Simulink实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
5.后端·新建子模块与开发(自动模式)
文章目录 学习资料自动生成模式创建后端三层 学习资料 https://www.bilibili.com/video/BV13g411Y7GS?p11&spm_id_frompageDriver&vd_sourceed09a620bf87401694f763818a31c91e 自动生成模式创建后端三层 首先,运行起来若依的前后端整个项目,…...
这样而不是data:{}这样?)
vue的data为什么要写成data(return{})这样而不是data:{}这样?
在Vue.js中,为什么要将data写成一个返回对象的函数data()而不是一个普通的对象data: {} 为什么? 因为Vue.js的组件实例是可复用的,而且它们可以在应用中多次实例化。通过将data定义为一个返回对象的函数,可以确保每个组件实例都…...

MySQL基础运维知识点大全
一. MySQL基本知识 1. 目录的功能 通用 Unix/Linux 二进制包的 MySQL 安装下目录的相关功能 目录目录目录binMySQLd服务器,客户端和实用程序docs信息格式的 MySQL 手册manUnix 手册页include包括(头)文件lib图书馆share用于数据库安装的错…...

javascript获取样式表的规则及读取与写入
CSSStyleSheet是继承了StyleSheet的接口属性,它是用于找当前文档中的<link rel“” href“”…>这样文件的,有以下属性:lenght,cssRules,title,href,type,deleteRule,insertRule等 CSSStyleRule是继承于CSSRule,它是用于找<link re…...

什么是promise?
是JavaScript中用于处理异步操作的一种机制。 异步操作,例如从服务器获取数据、读取文件、执行数据库查询等等。 经典使用:Axios 是一个基于Promise的HTTP客户端 Promise具有三个状态: Pending(待定):Pr…...

从零开始学习软件测试-第45天笔记
monkey事件 事件:对app进行的操作,比如触摸事件,滑动事件...动作:构成一个事件所需要的步骤。 调整事件的百分比 adb shell monkey -p 包名 -v -v --pct-xxx 百分比 次数>输出文件的路径 分析日志有没有报错 到日志中去找…...

visual studio常用快捷键
CtrlM、CtrlO 折叠到定义 CtrlM、CtrlM 折叠当前定义 CtrlM、CtrlA 折叠全部 CtrlK、CtrlD 自动编排代码格式 F12 转到定义 ShiftF12 查看所有定义 ctrl] 转到定义首部或尾部 ctrlX 未选中文本时,剪切/删除光标所在行。ctrlV 未选中文本时,粘贴到…...

数据变换:数据挖掘的准备工作之一
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据…...

Go语言实践案例之简单字典
一、程序要实现效果: 在命令行调用程序的时候,可以在命令行的后面查询一个单词,然后会输出单词的音标和注释。 二、思路分析: 定义一个结构体 DictRequest,用于表示翻译请求的数据结构。其中包含了 TransType&#…...
)
笔试面试相关记录(3)
(1)String String和String.append()的底层实现 C中string append函数的使用与字符串拼接「建议收藏」-腾讯云开发者社区-腾讯云 (tencent.com) String String 在 第二个String中遇到\0就截止,append()的方法则是所有字符都会加在后面。 &…...
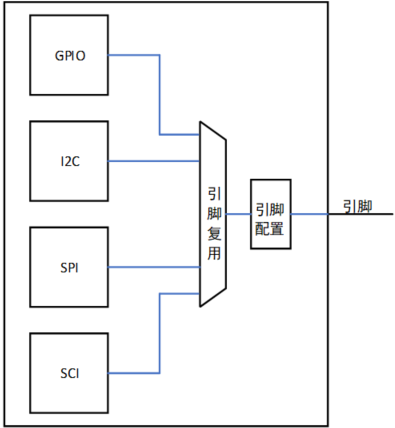
第6章_瑞萨MCU零基础入门系列教程之串行通信接口(SCI)
本教程基于韦东山百问网出的 DShanMCU-RA6M5开发板 进行编写,需要的同学可以在这里获取: https://item.taobao.com/item.htm?id728461040949 配套资料获取:https://renesas-docs.100ask.net 瑞萨MCU零基础入门系列教程汇总: ht…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...
