考研408 | 【计算机组成原理】 数据的表示和运算
进位计数制
十进制计数法:
推广:r进制计数法
任意进制-->十进制:
二进制<-->八进制、十六进制:

各种进制的常见书写方式:
十进制-->任意进制:

十进制-->二进制(拼凑法):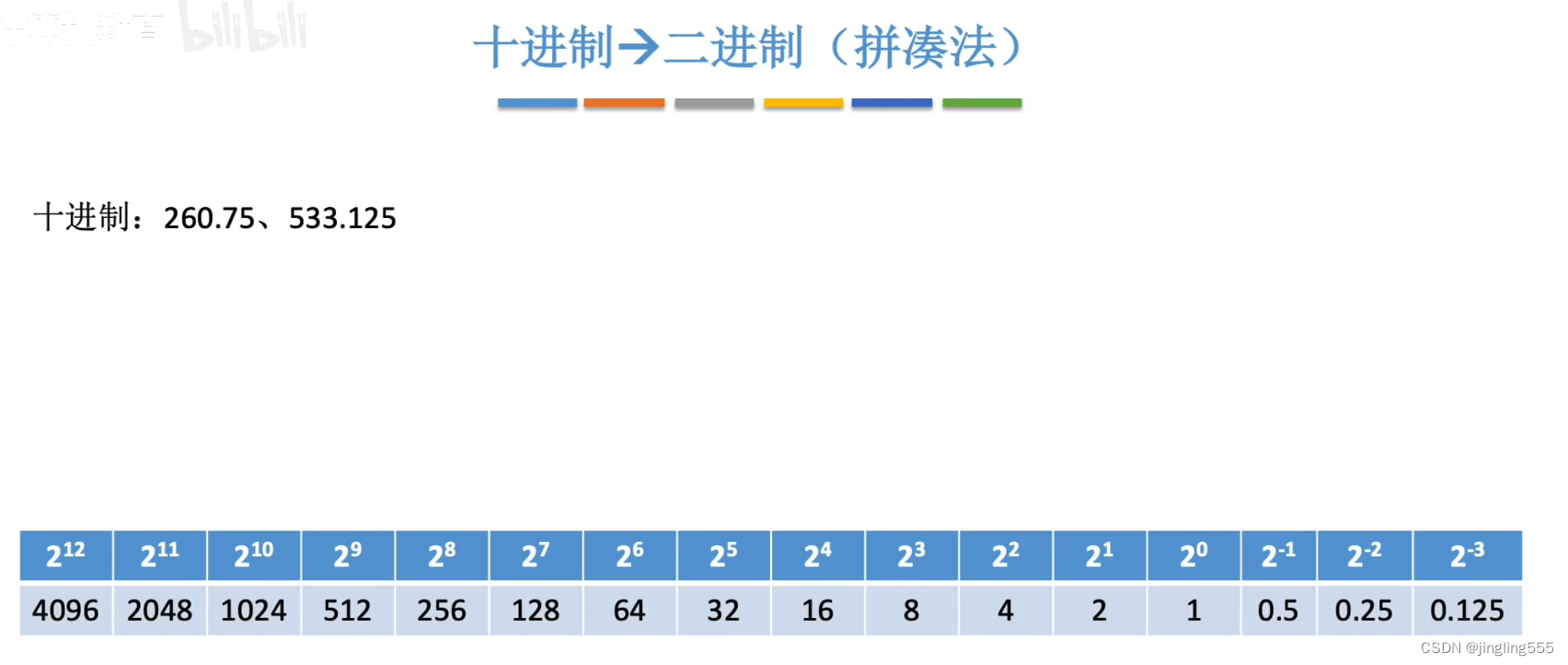
真值和机器数:
总结: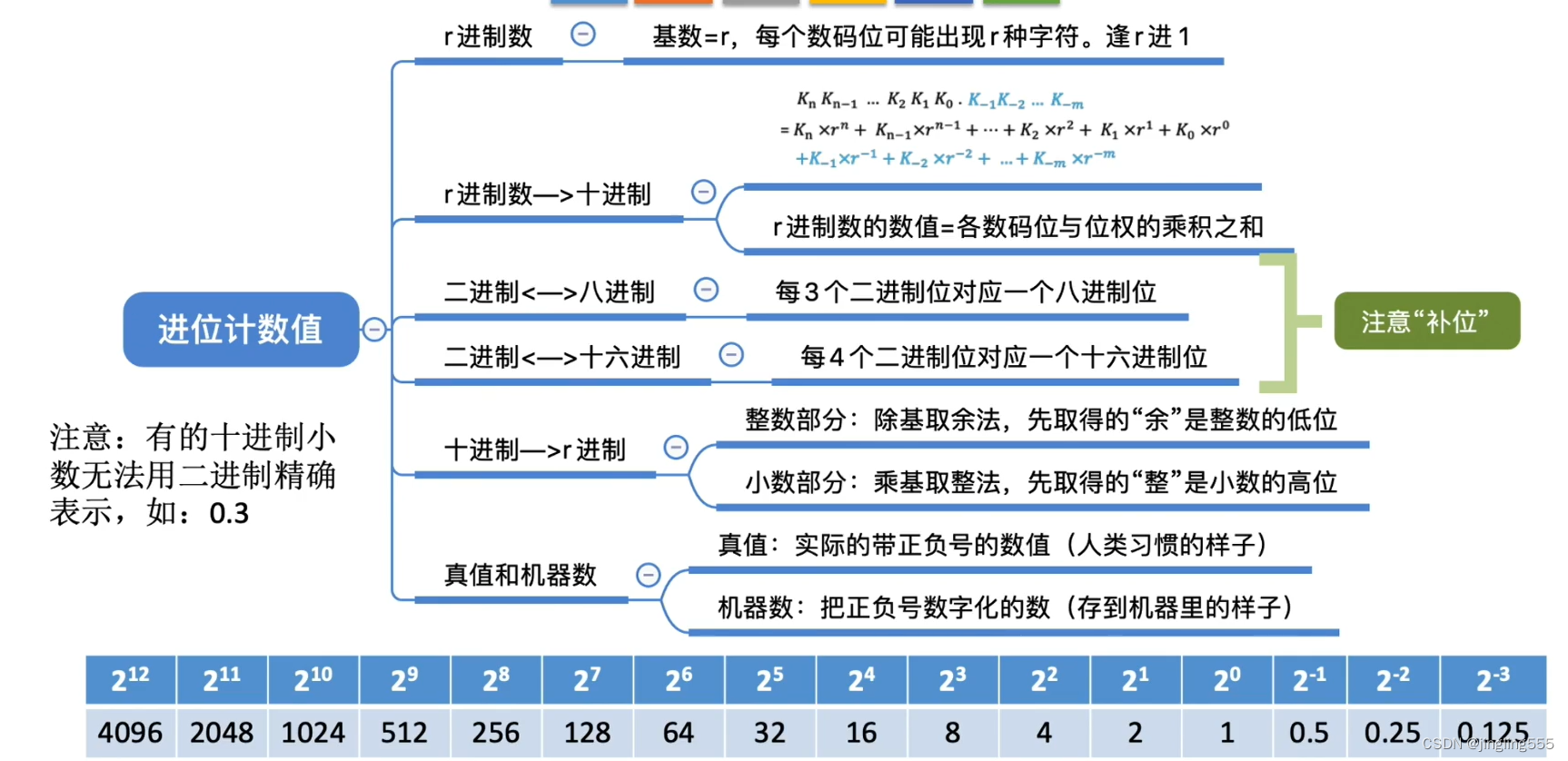
BCD码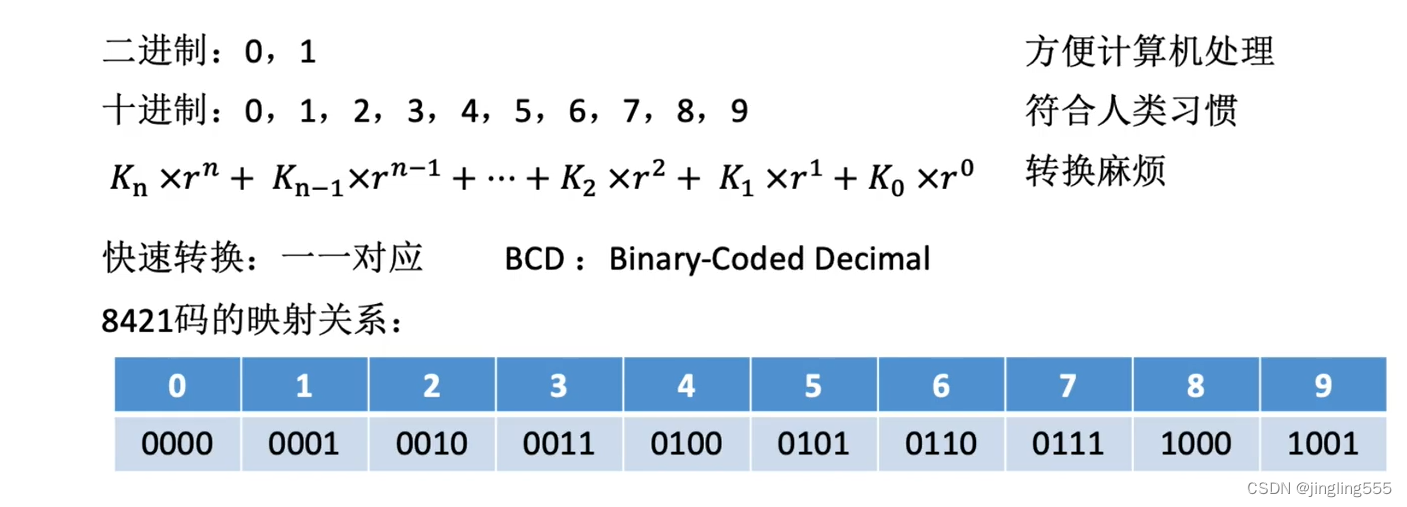
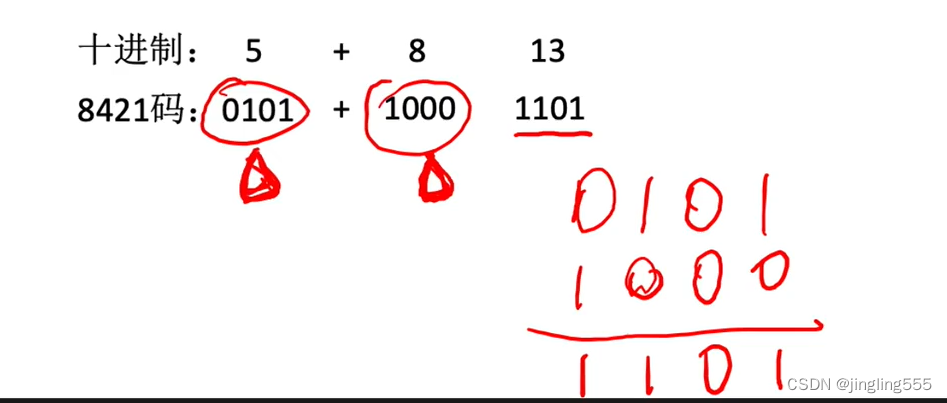

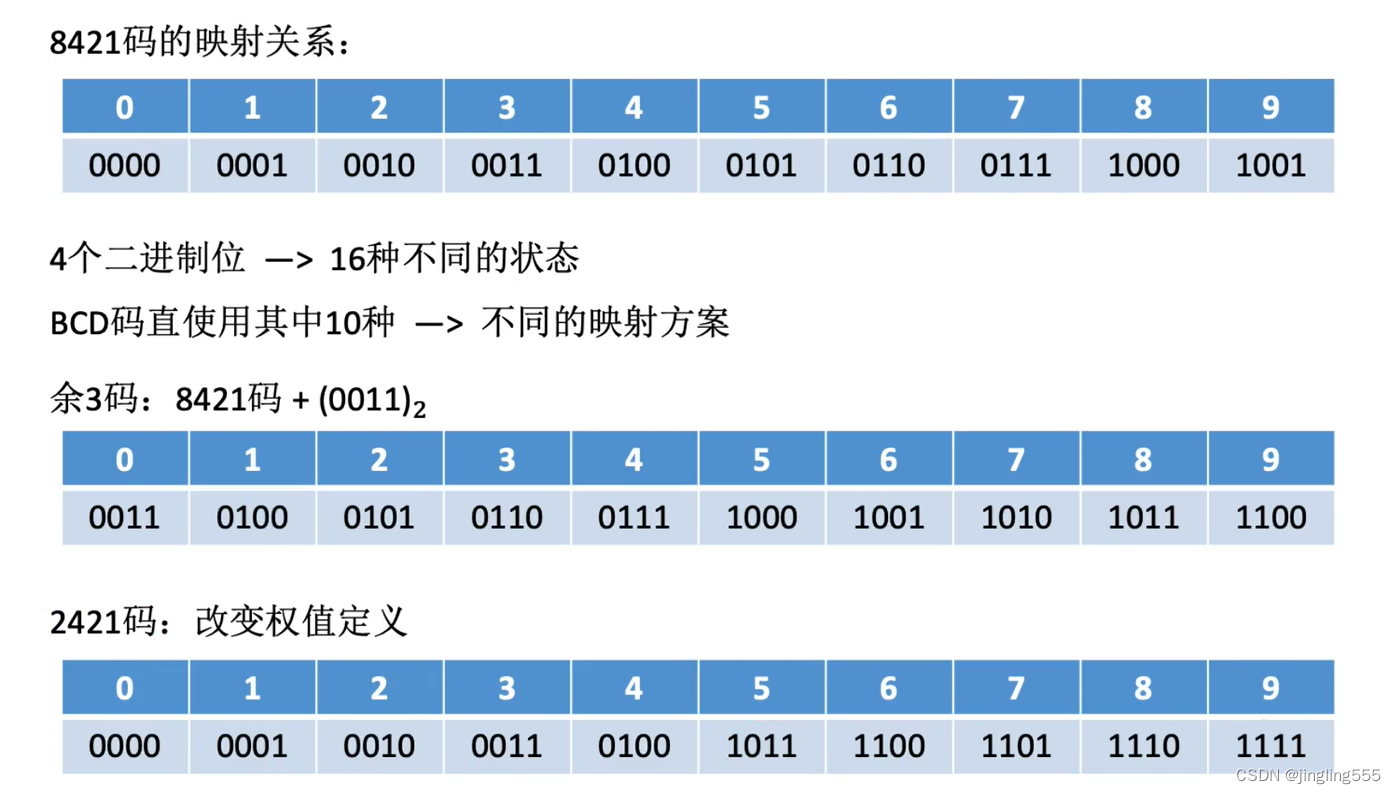
总结: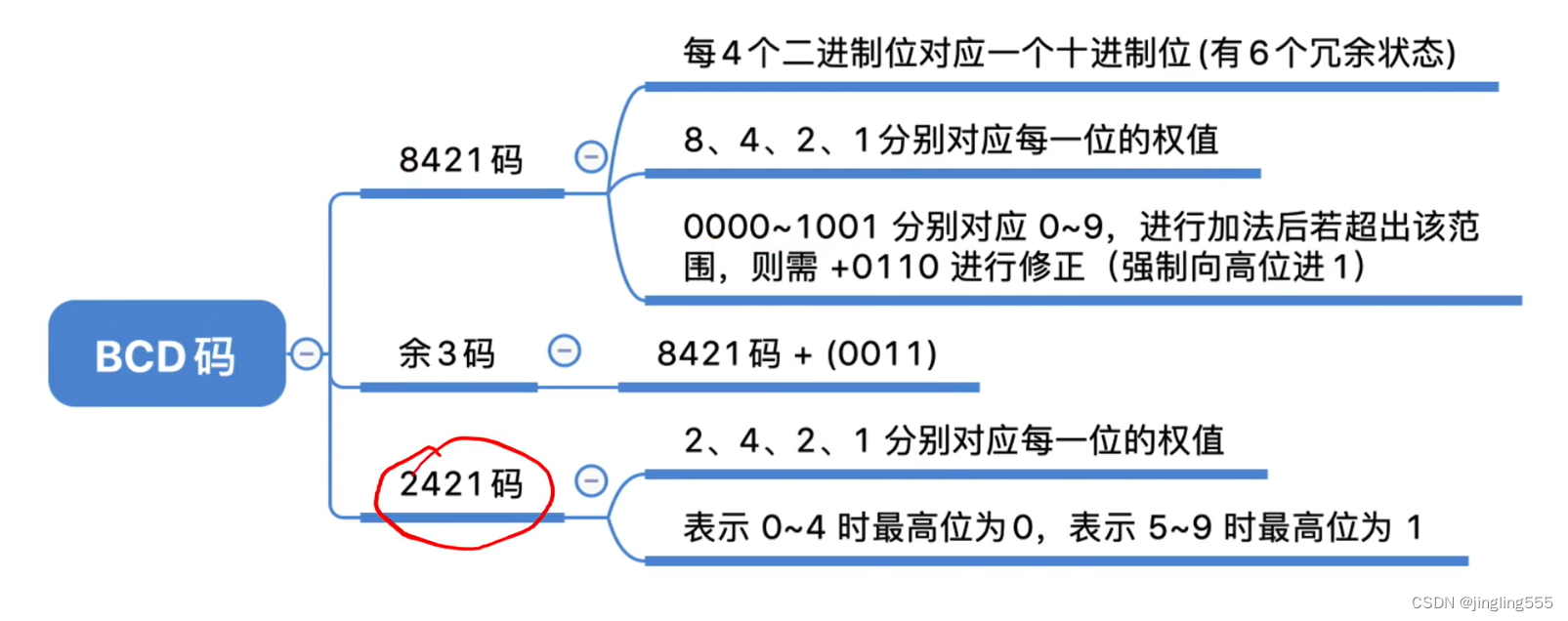
无符号整数的表示和运算
无符号整数在计算机中的应用:
无符号整数的表示: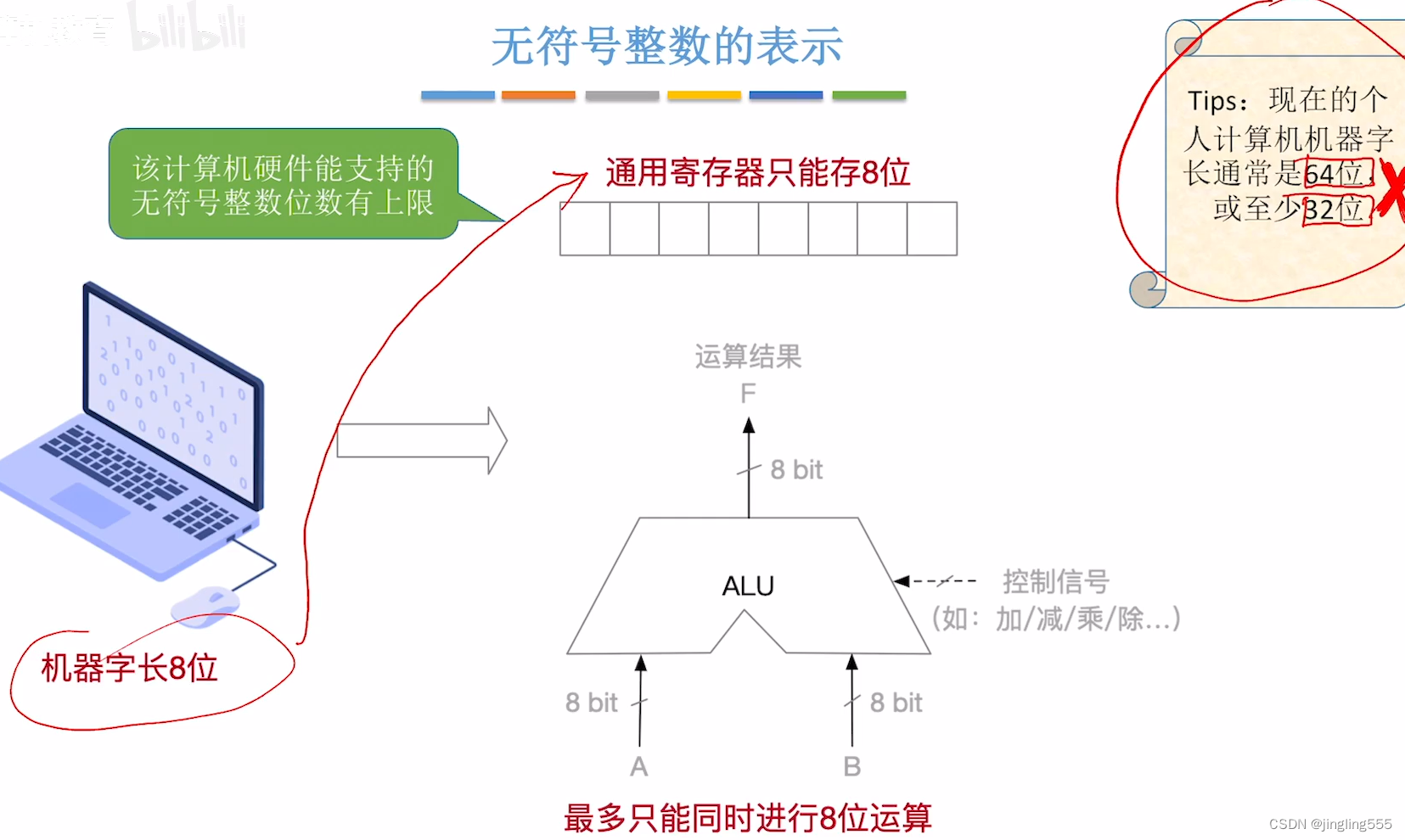
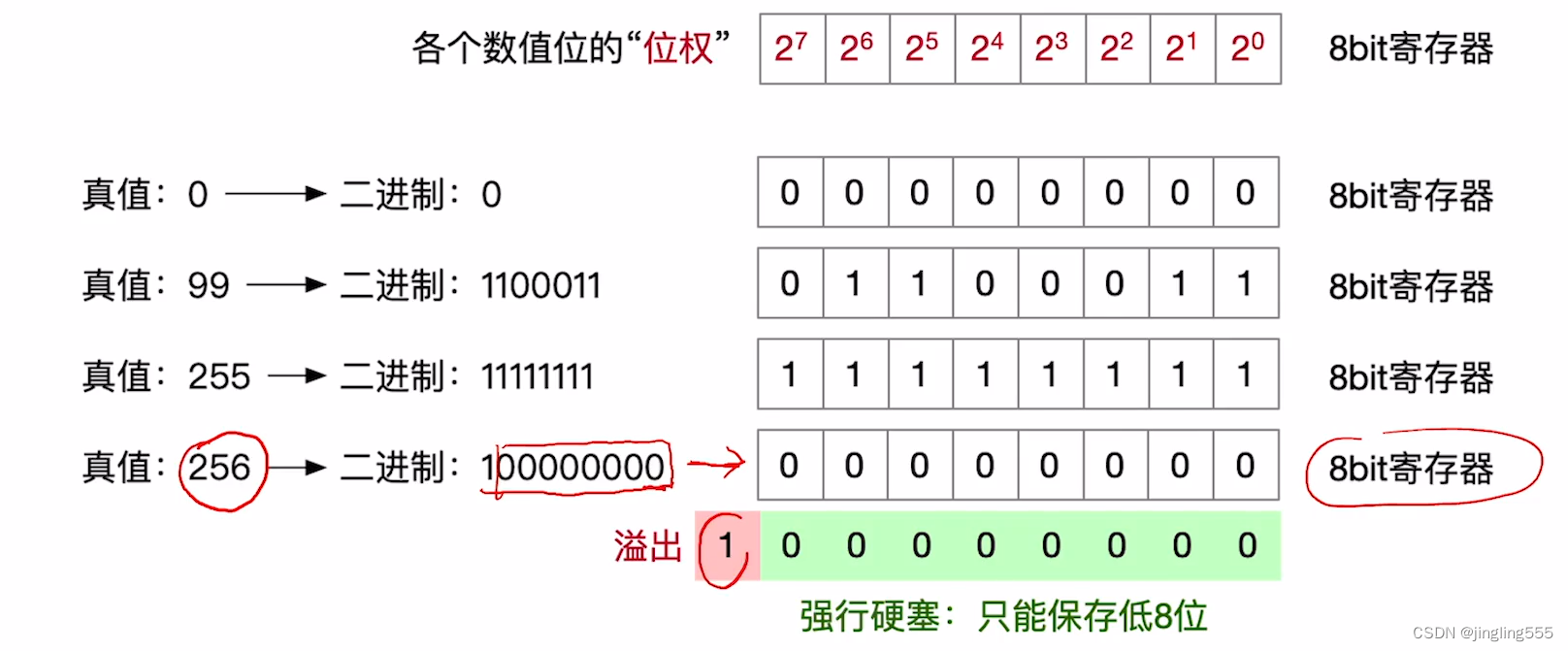

无符号整数的加法运算:
无符号整数的减法运算: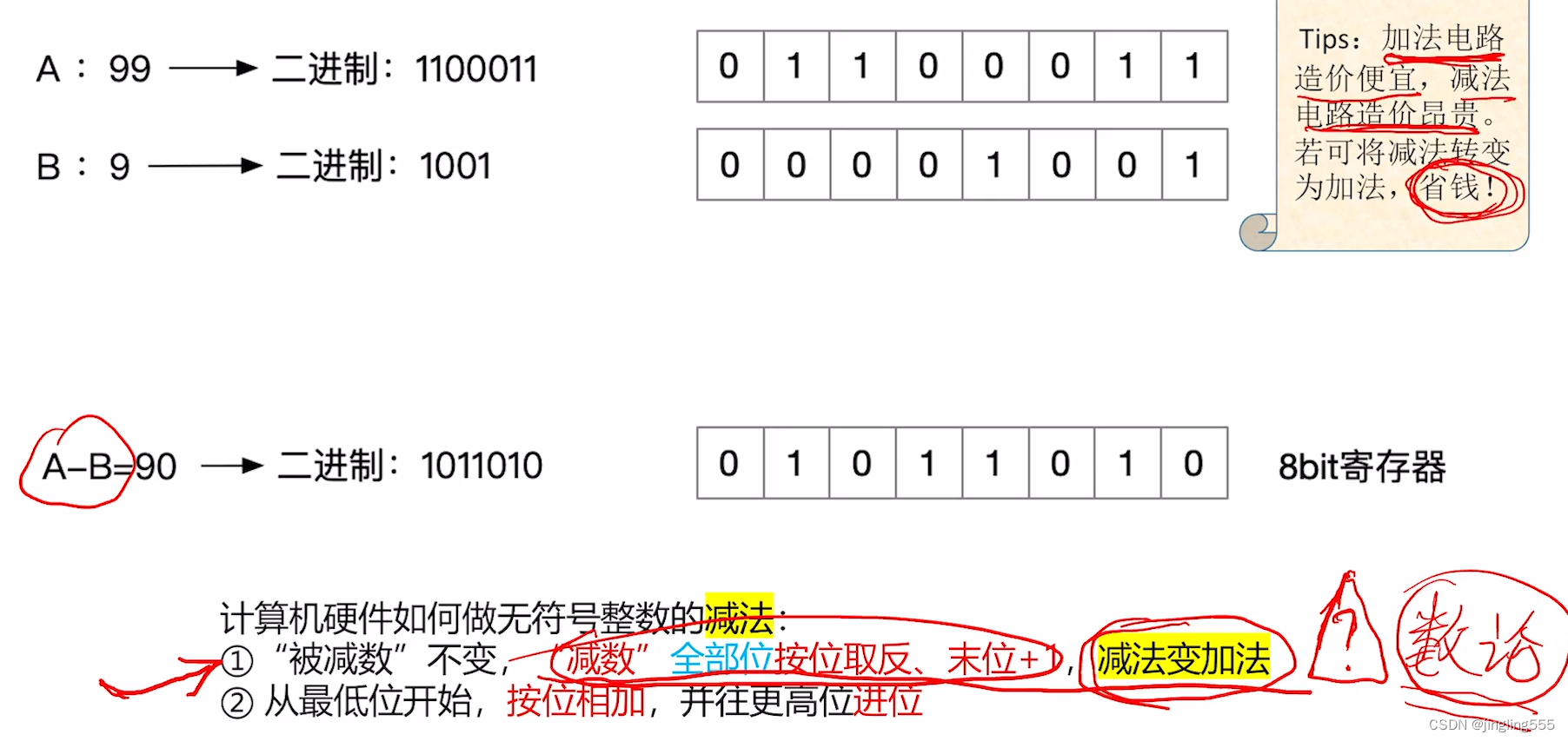
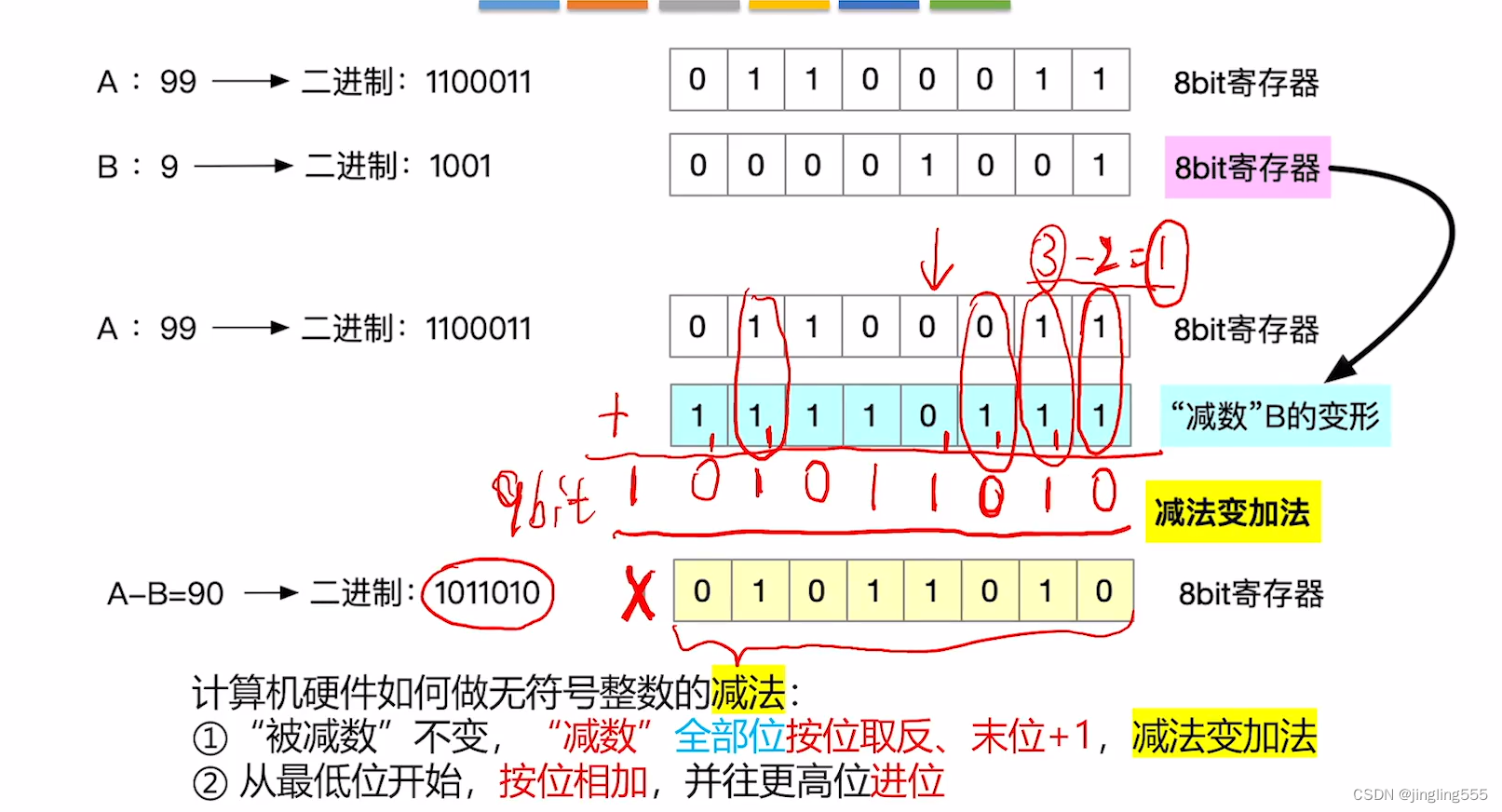
总结:
带符号整数的表示和运算(原、反,补码)
带符号整数的表示: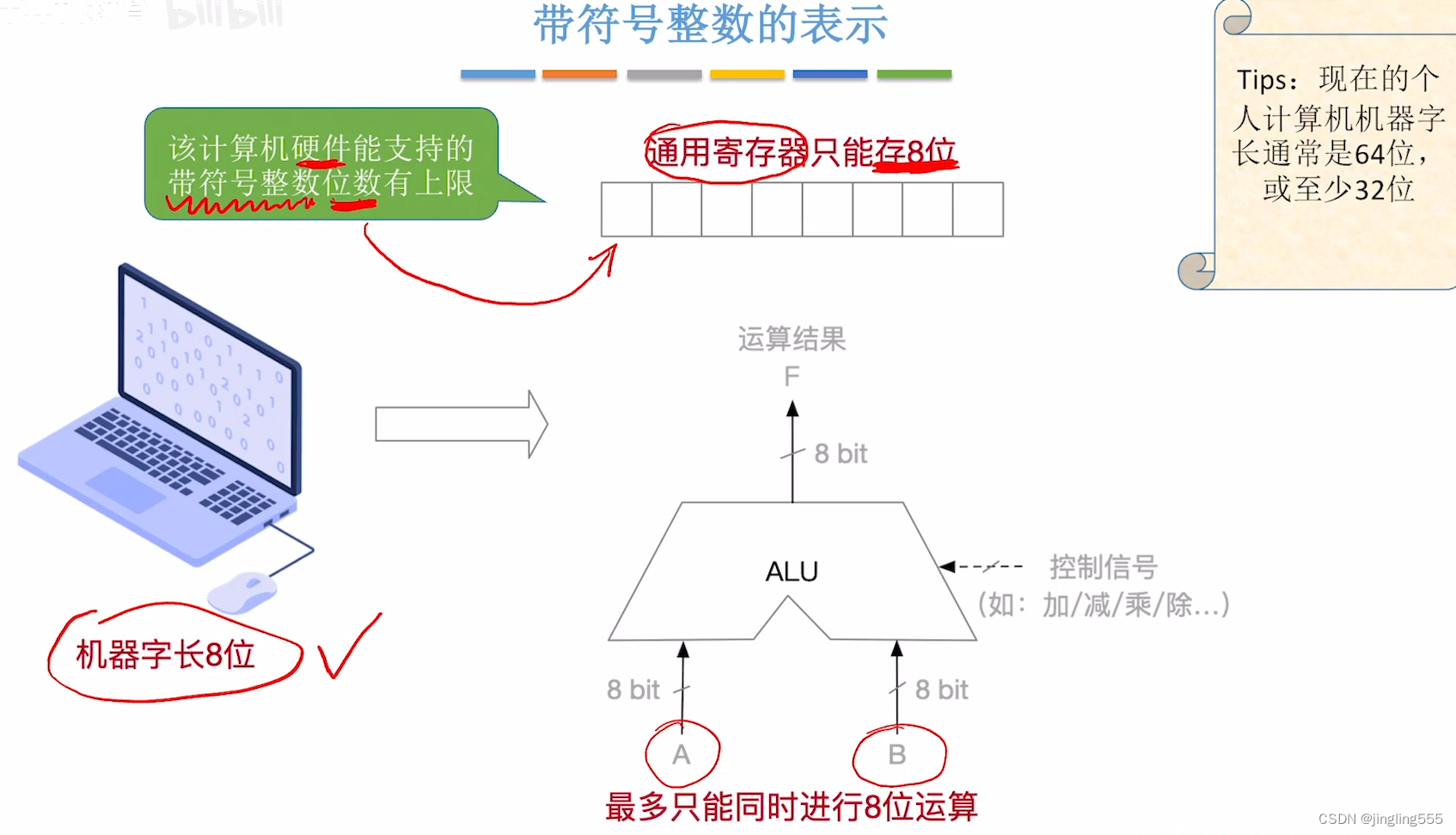
原码表示: 
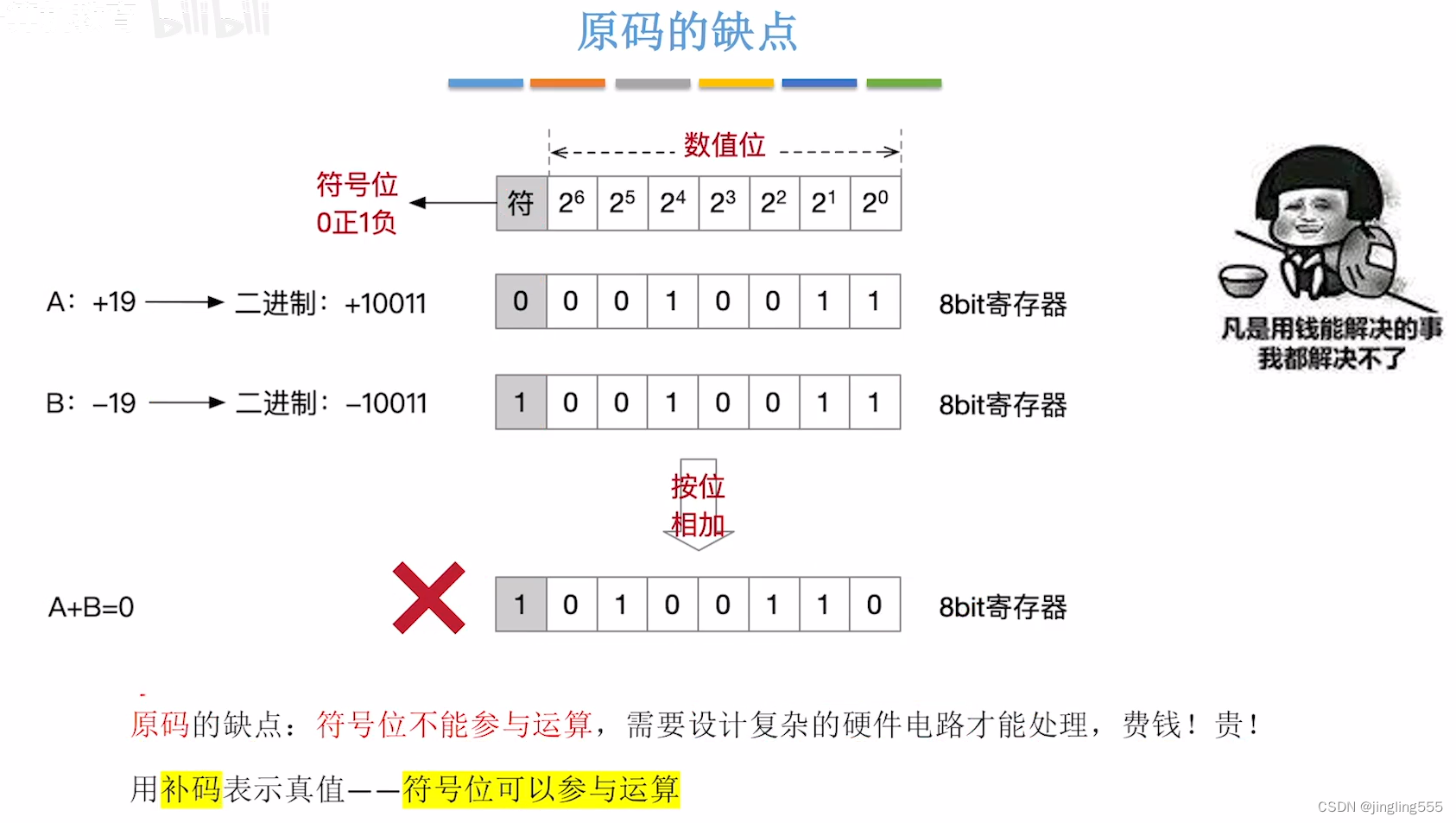
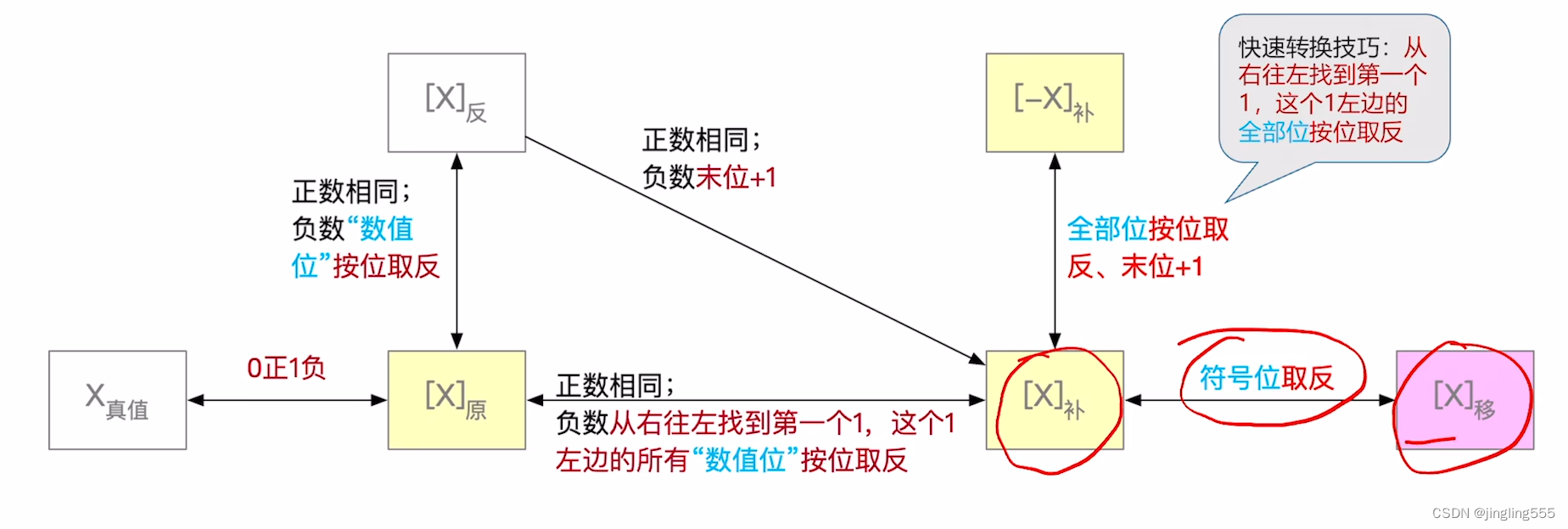
原码-->反码-->补码的转换: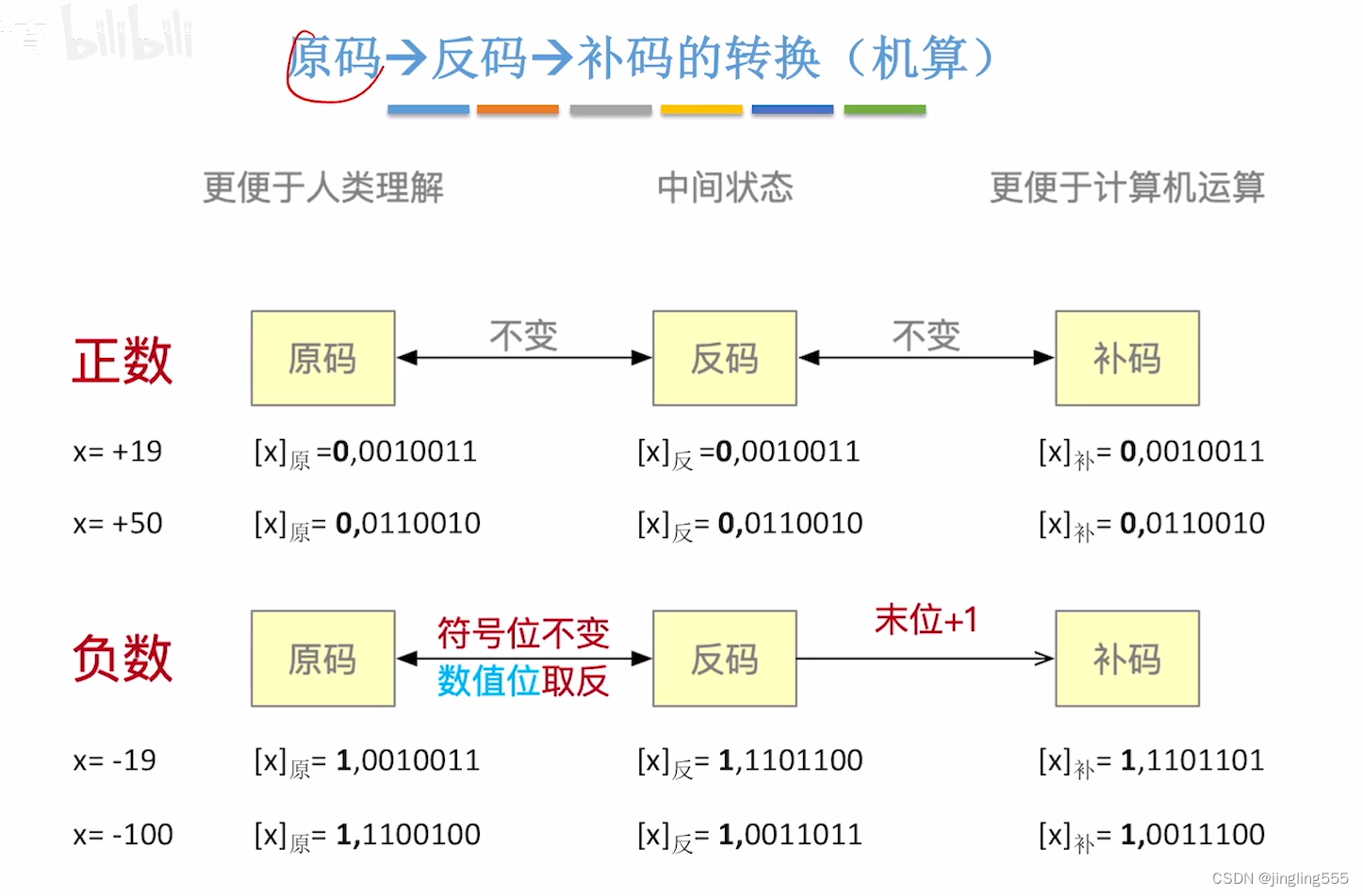
快速手算技巧: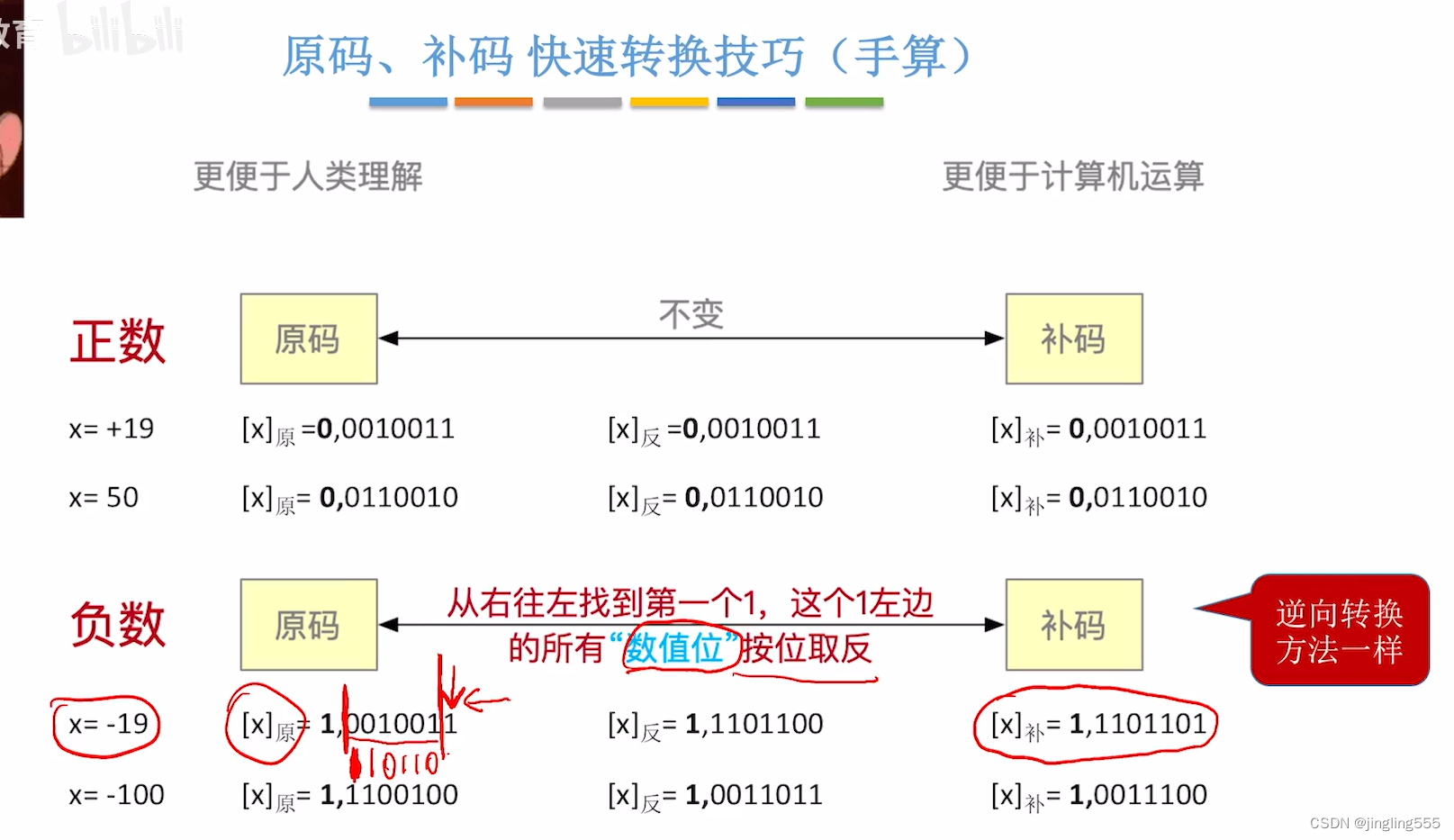
补码的加法运算: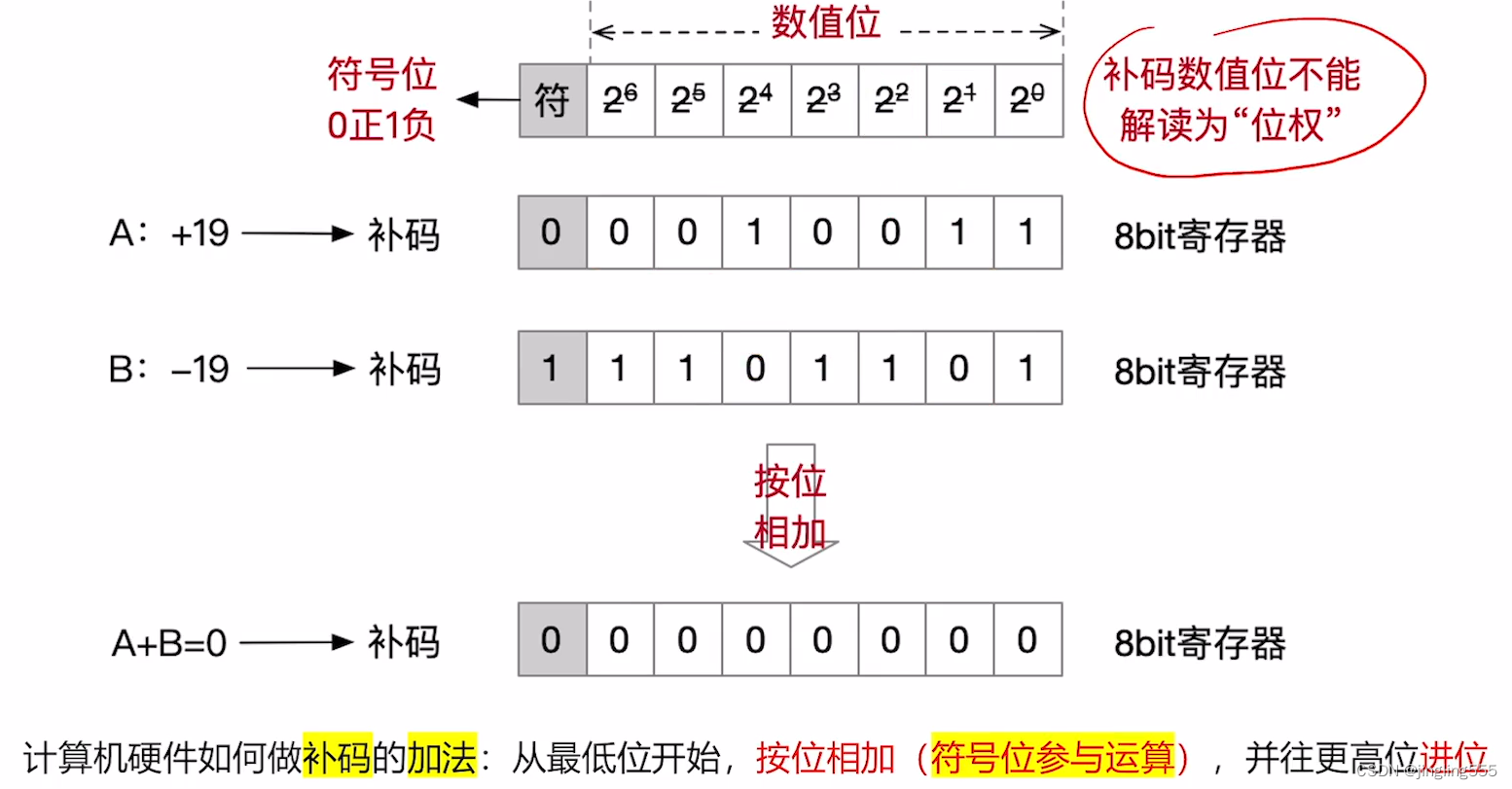
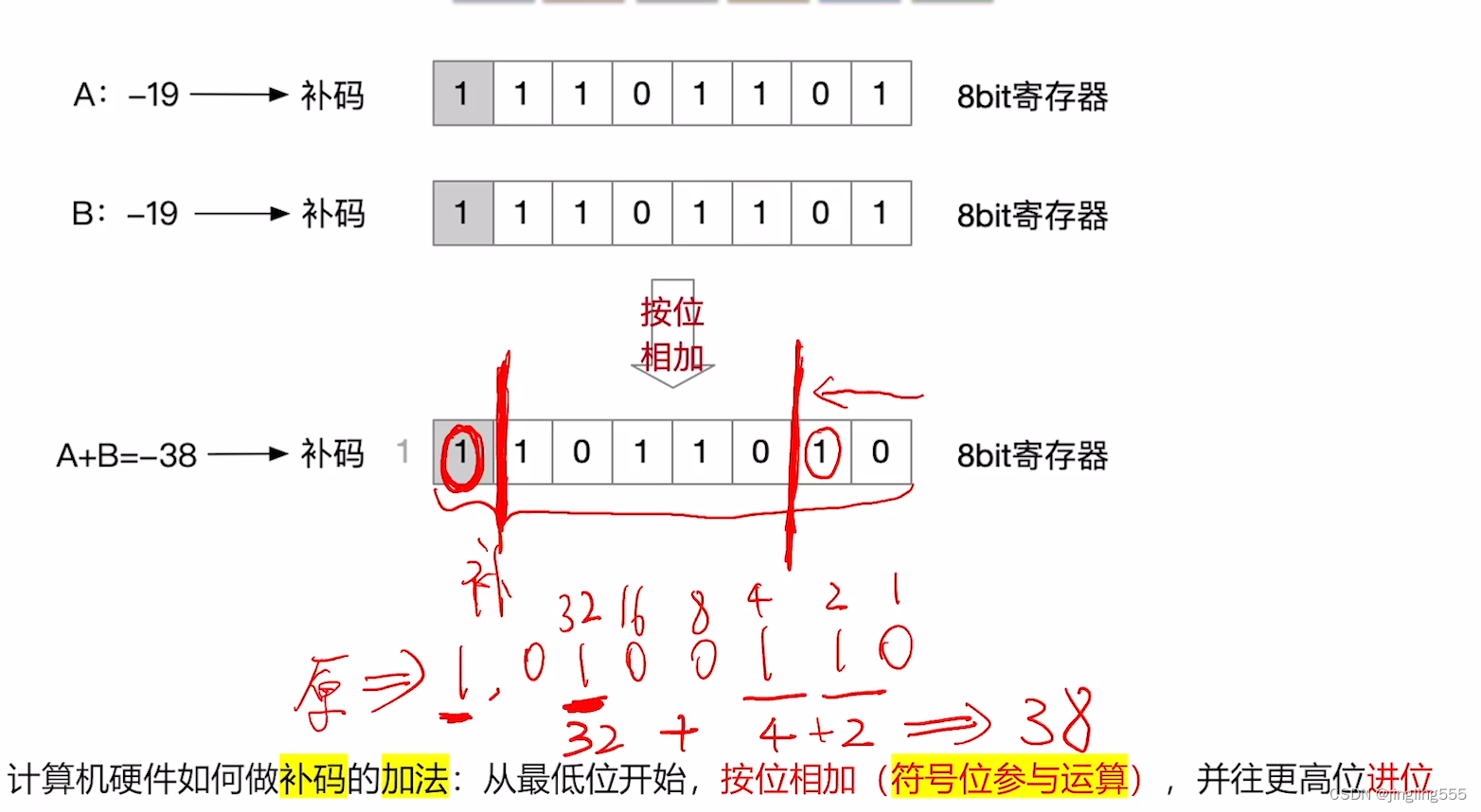
补码的减法运算: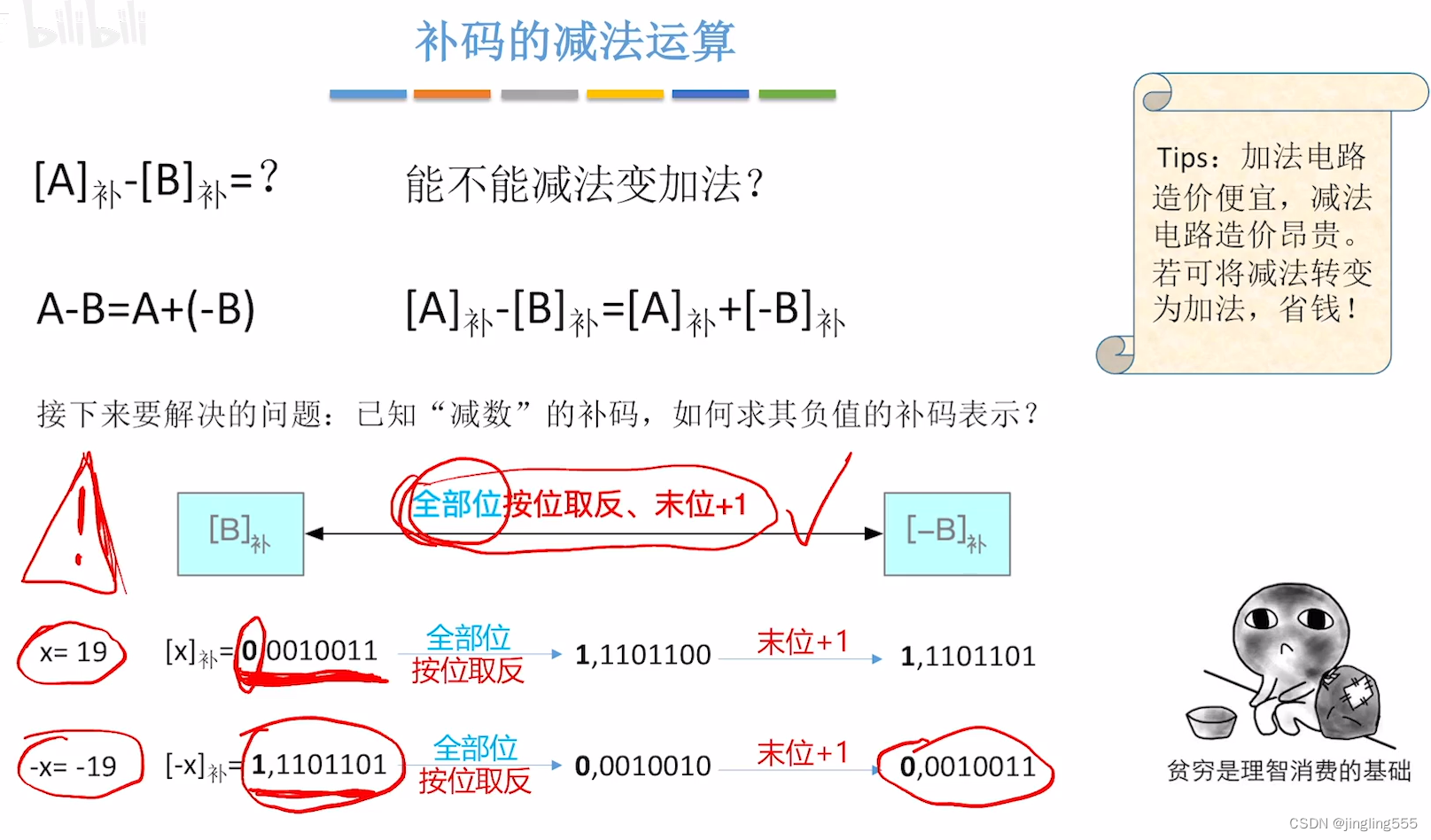

总结: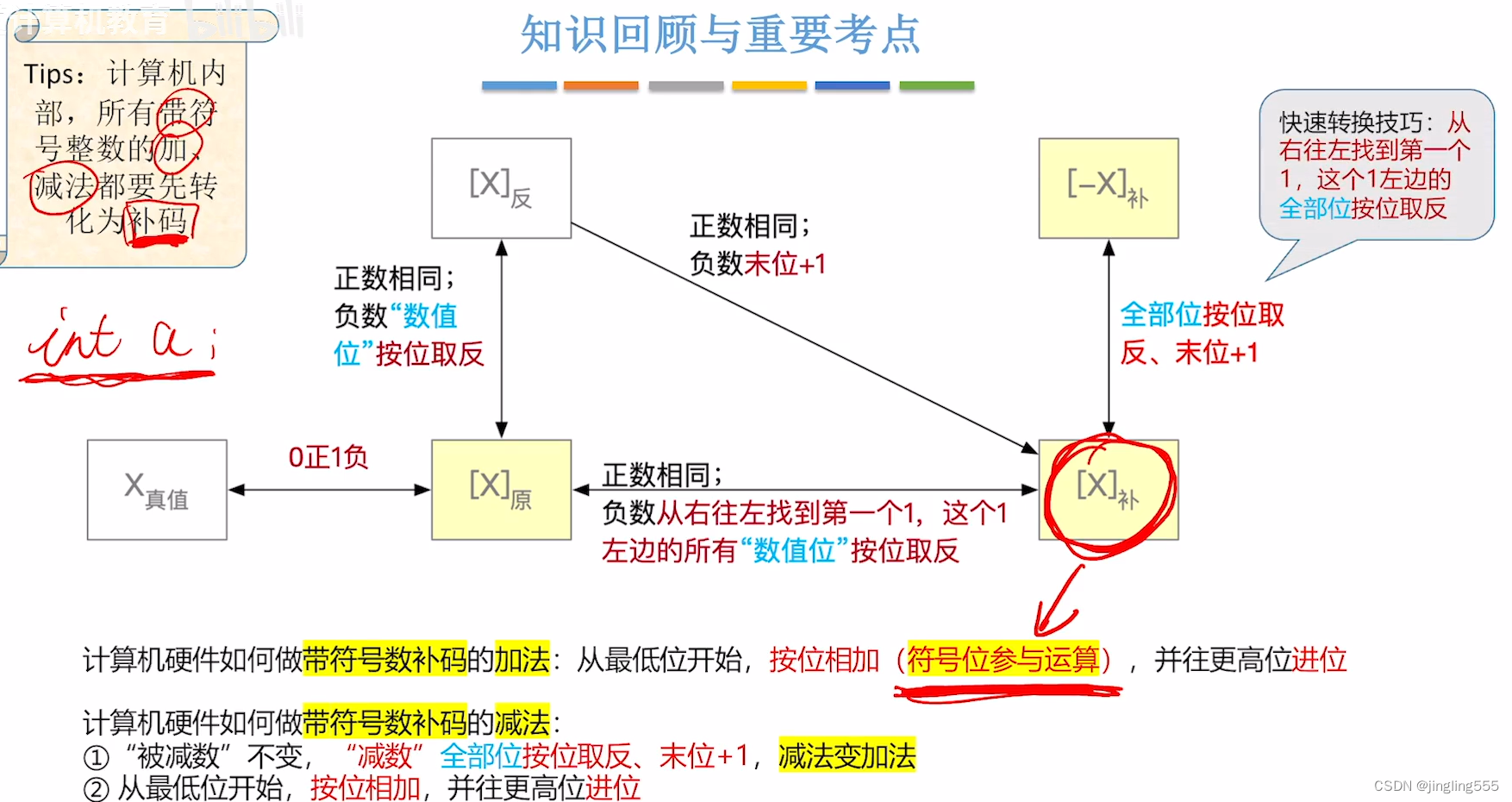
几种码的特性对比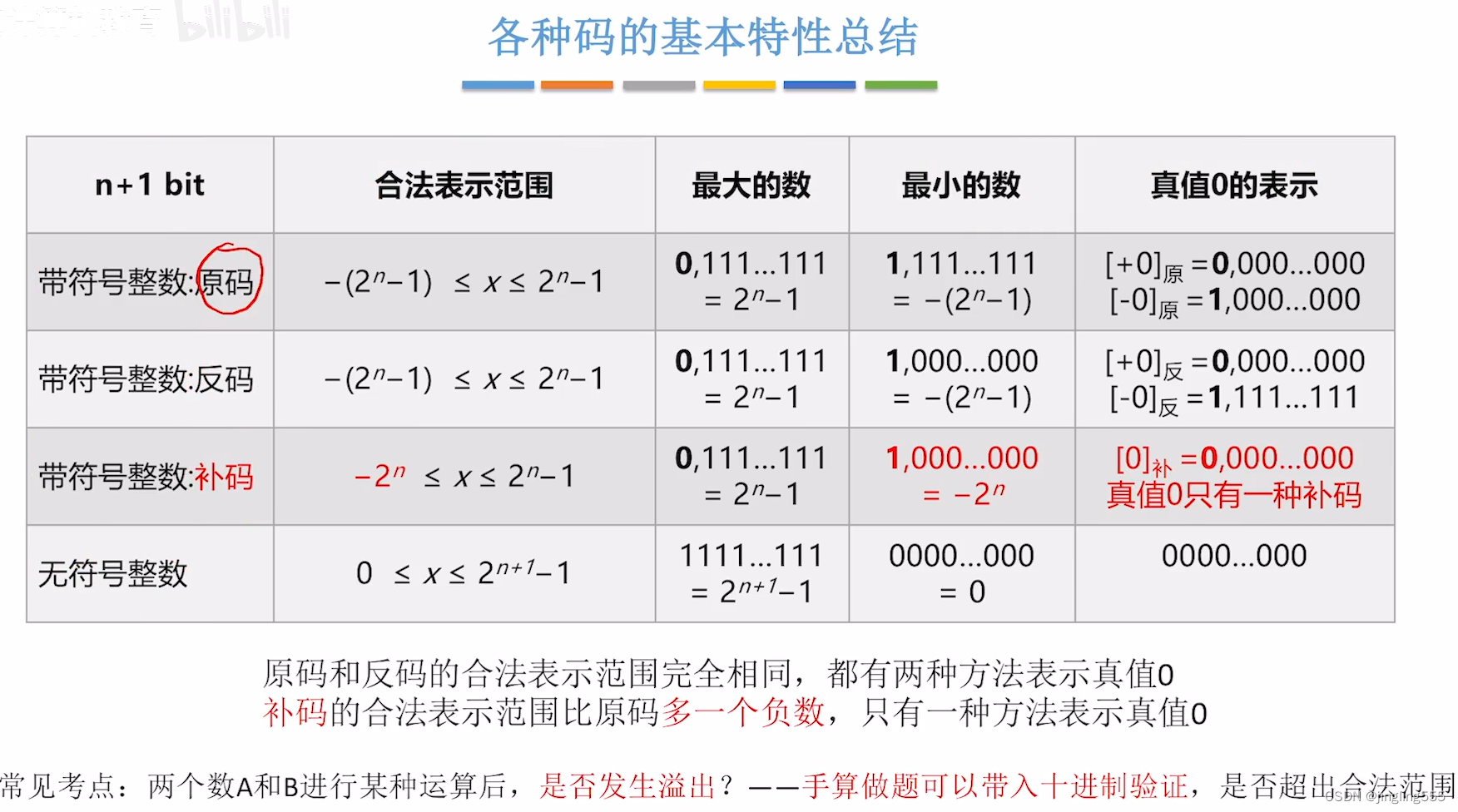
移码
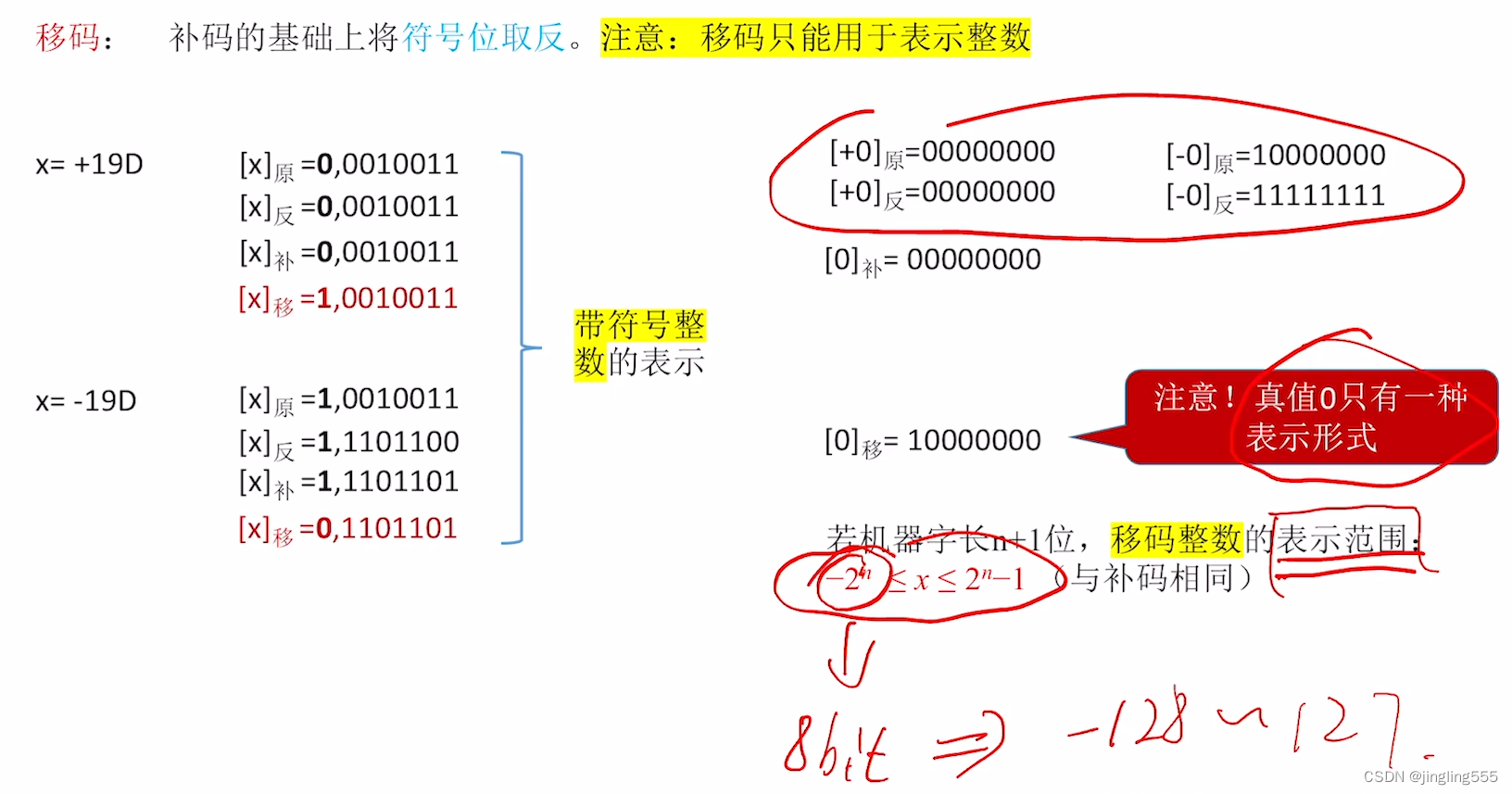
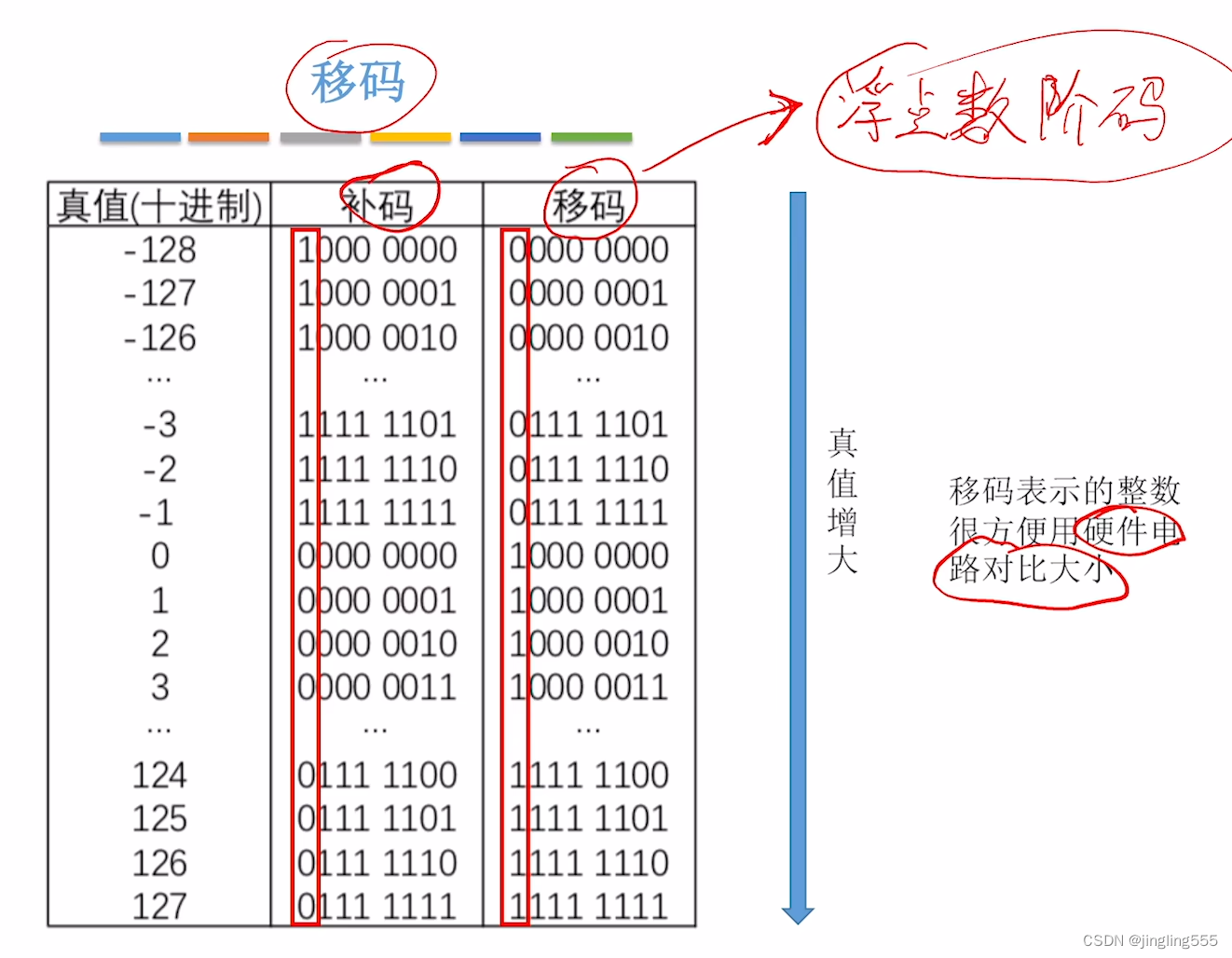
用几种码表示整数: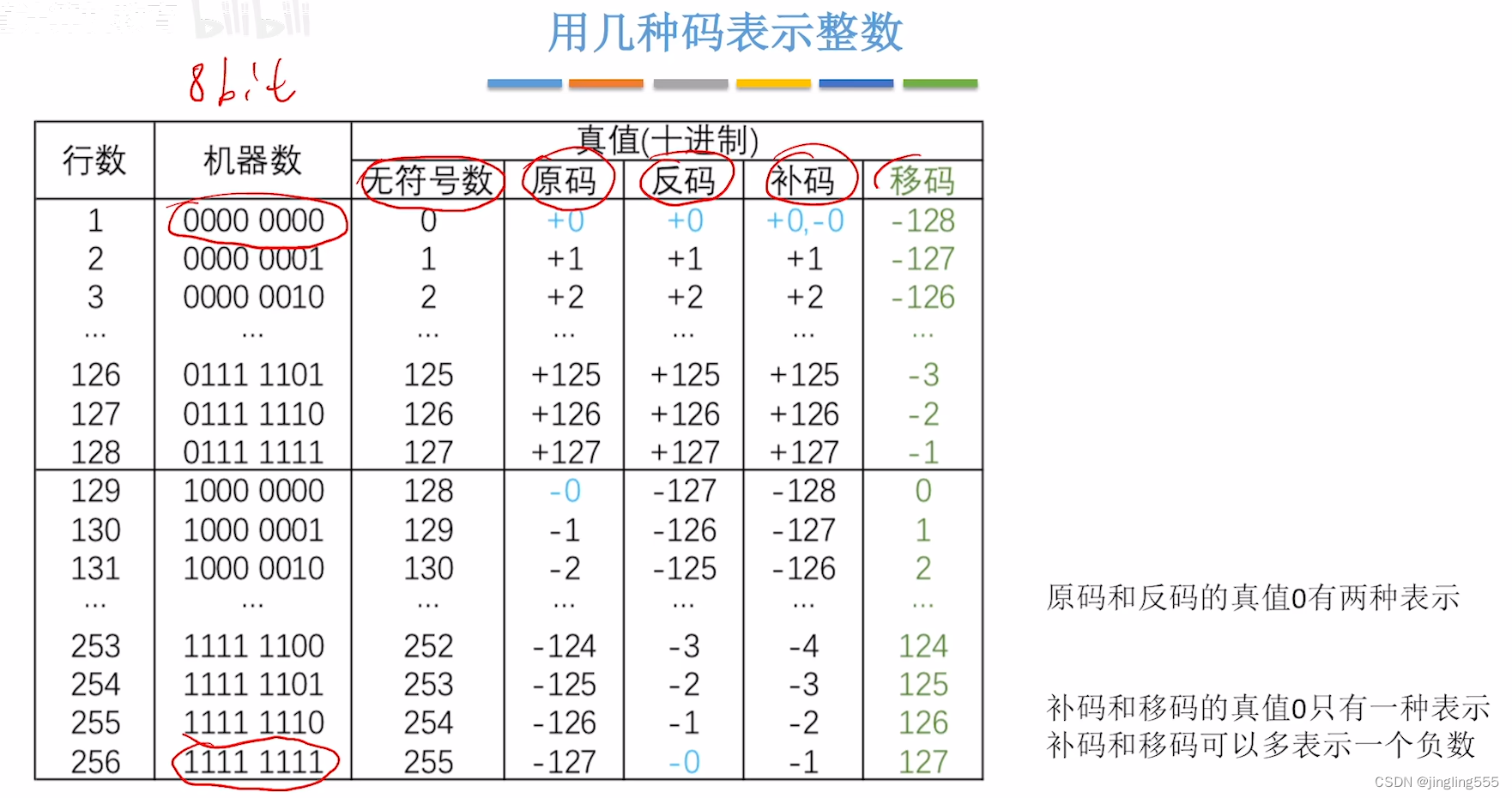
题目: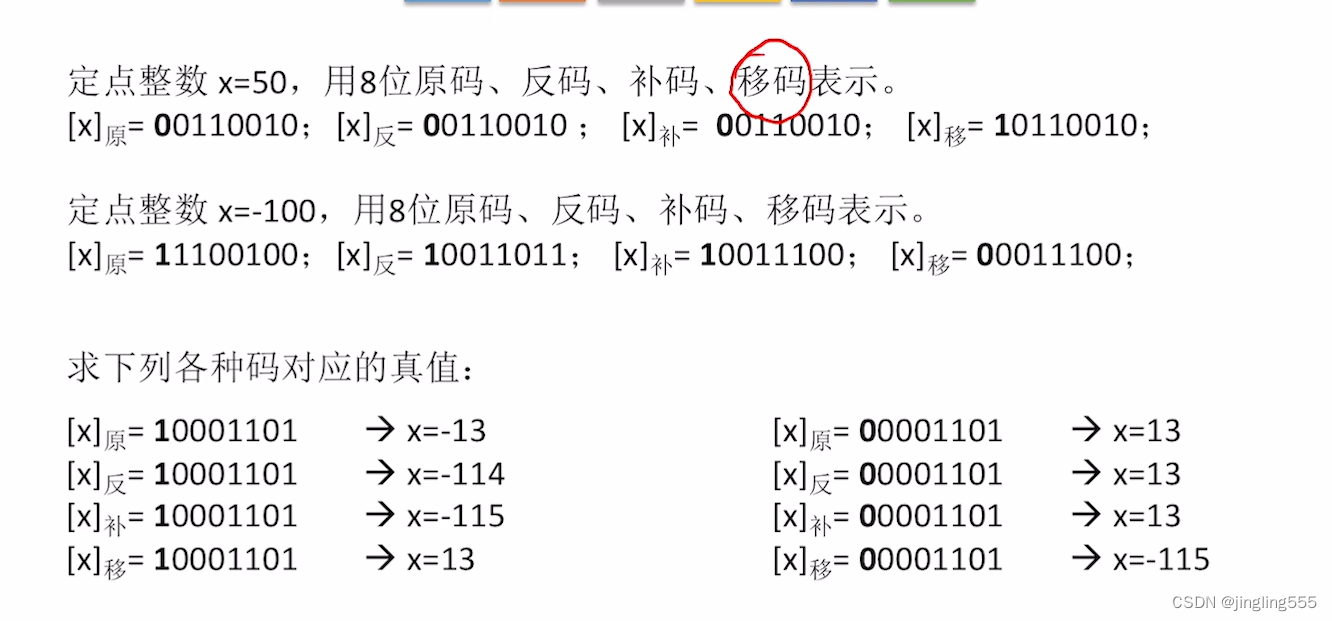
各种码的基本特性总结: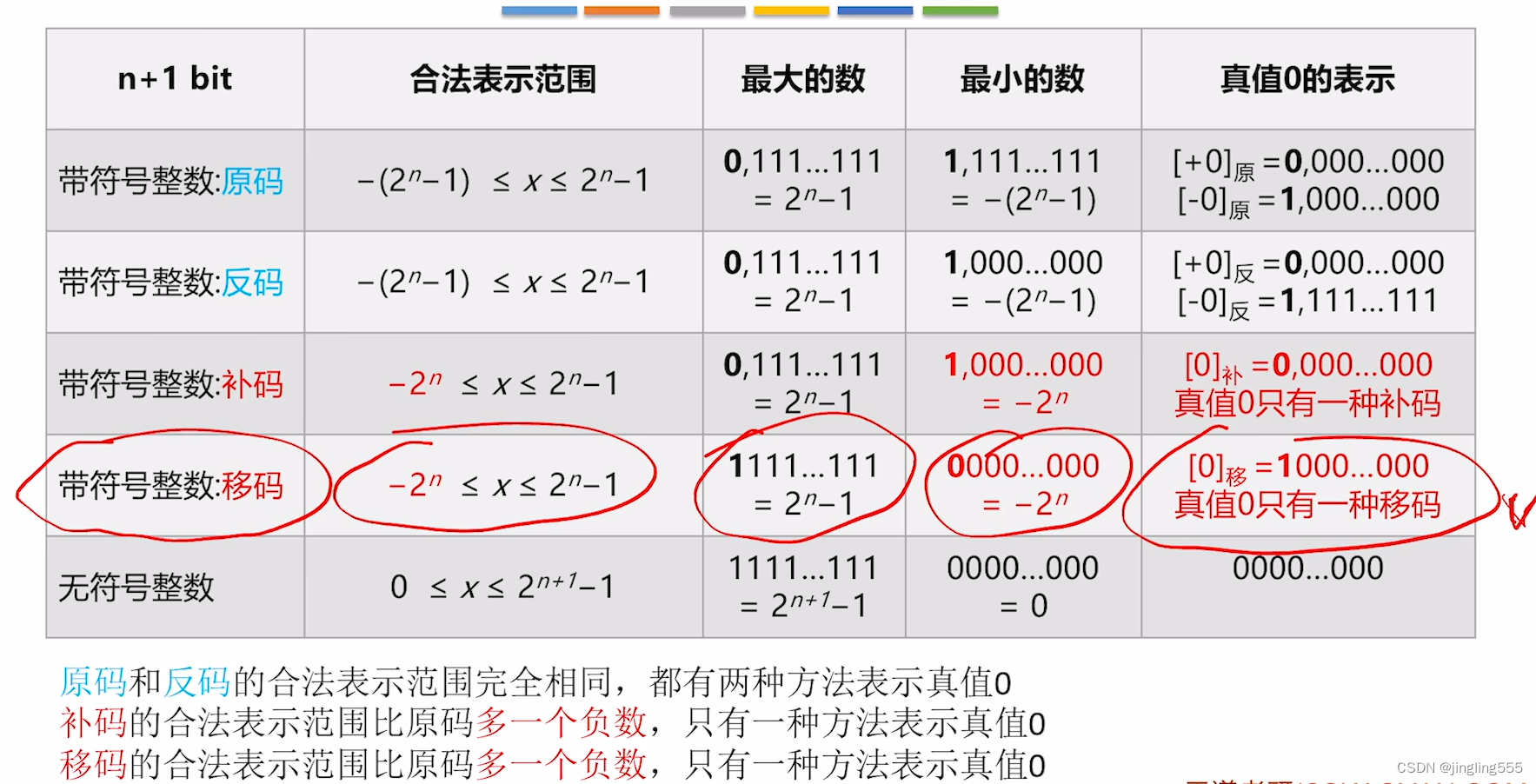
定点小数的表示和运算
定点整数、定点小数: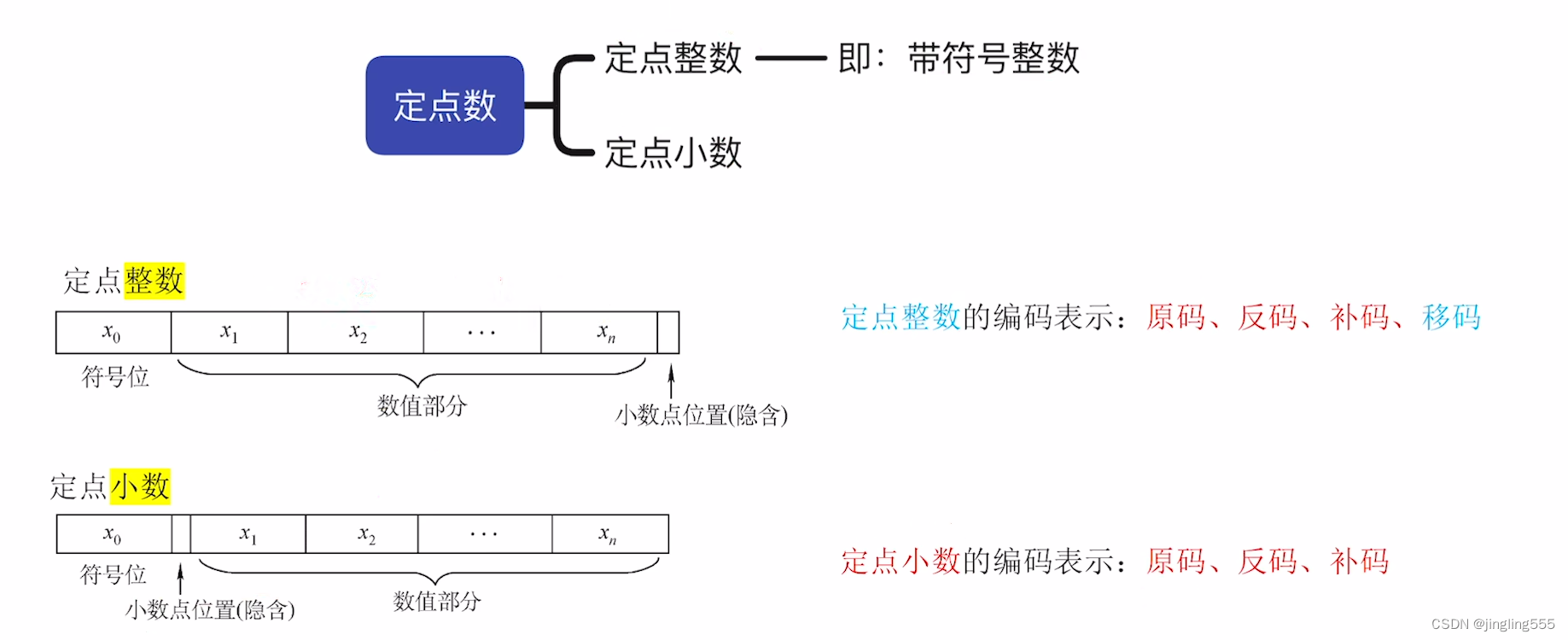
原码: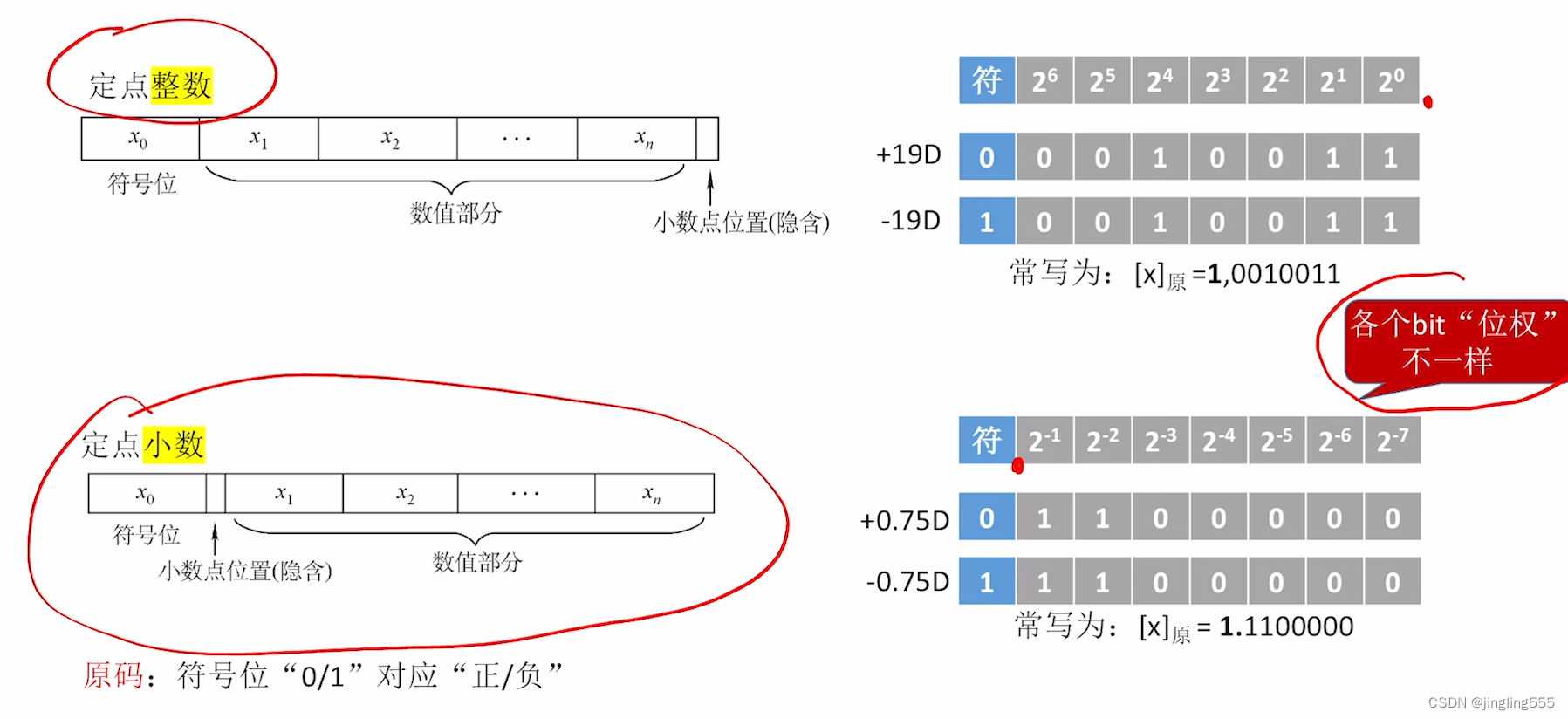
定点小数原/反/补码的转换: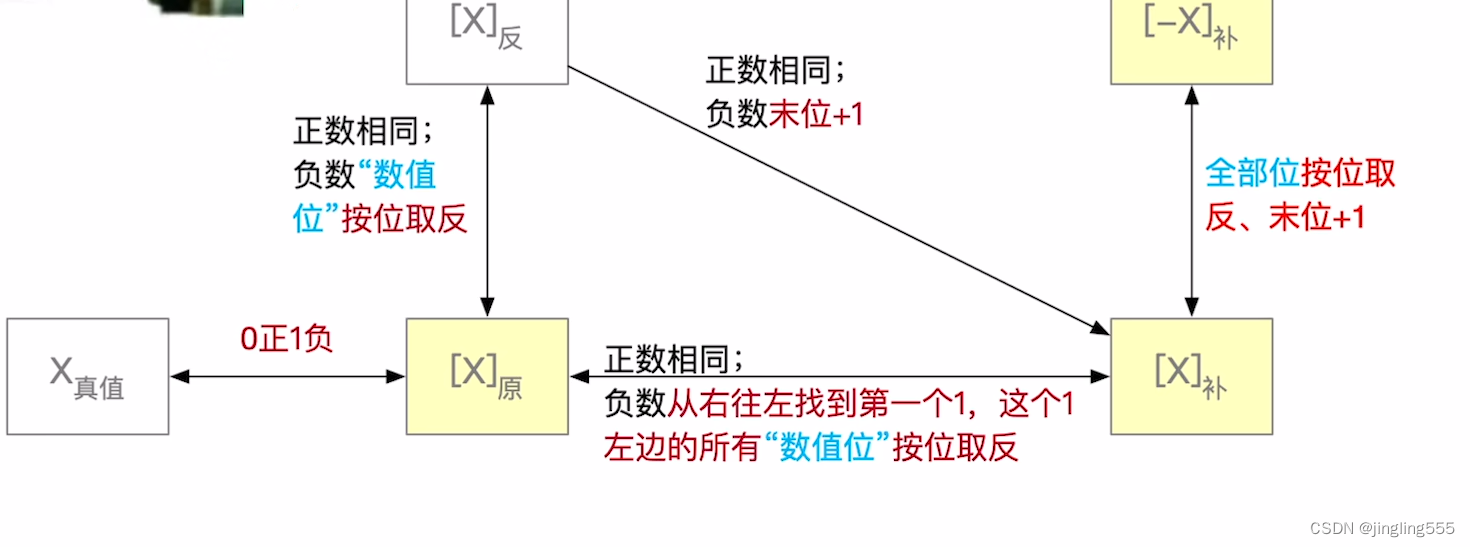
定点小数的加/减运算:
定点小数VS定点整数: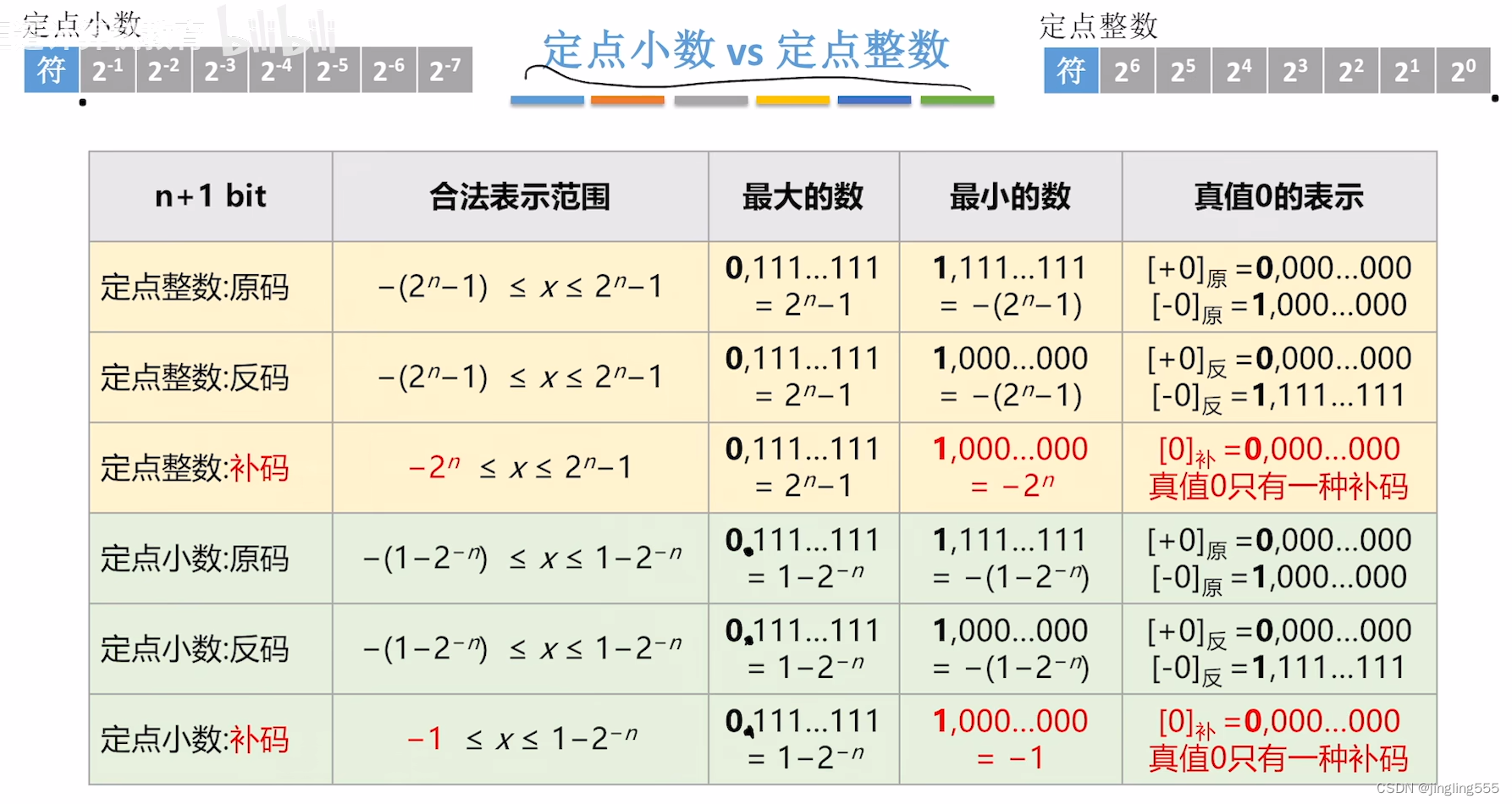

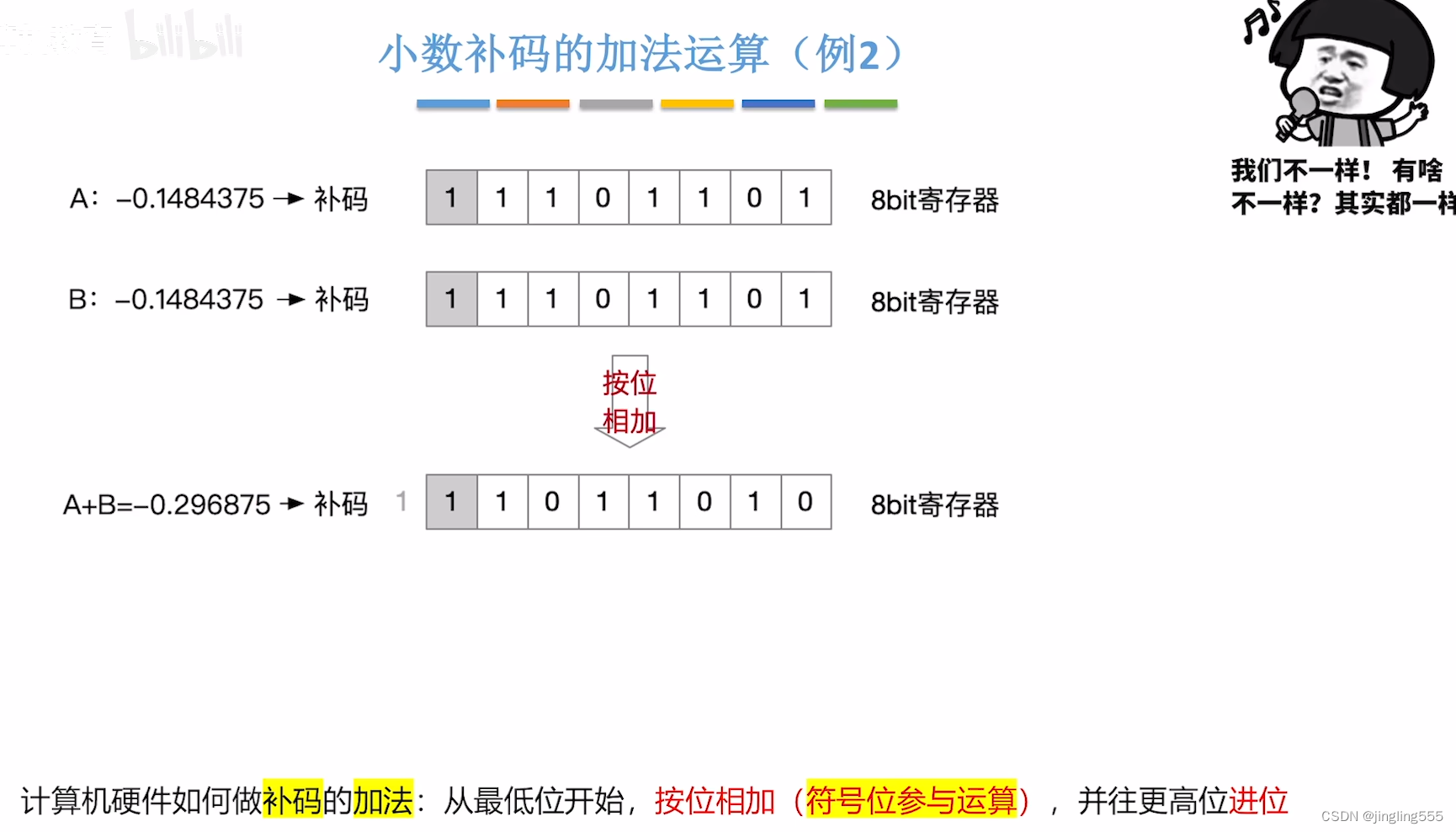
小数补码的加法运算:
小数补码的减法运算: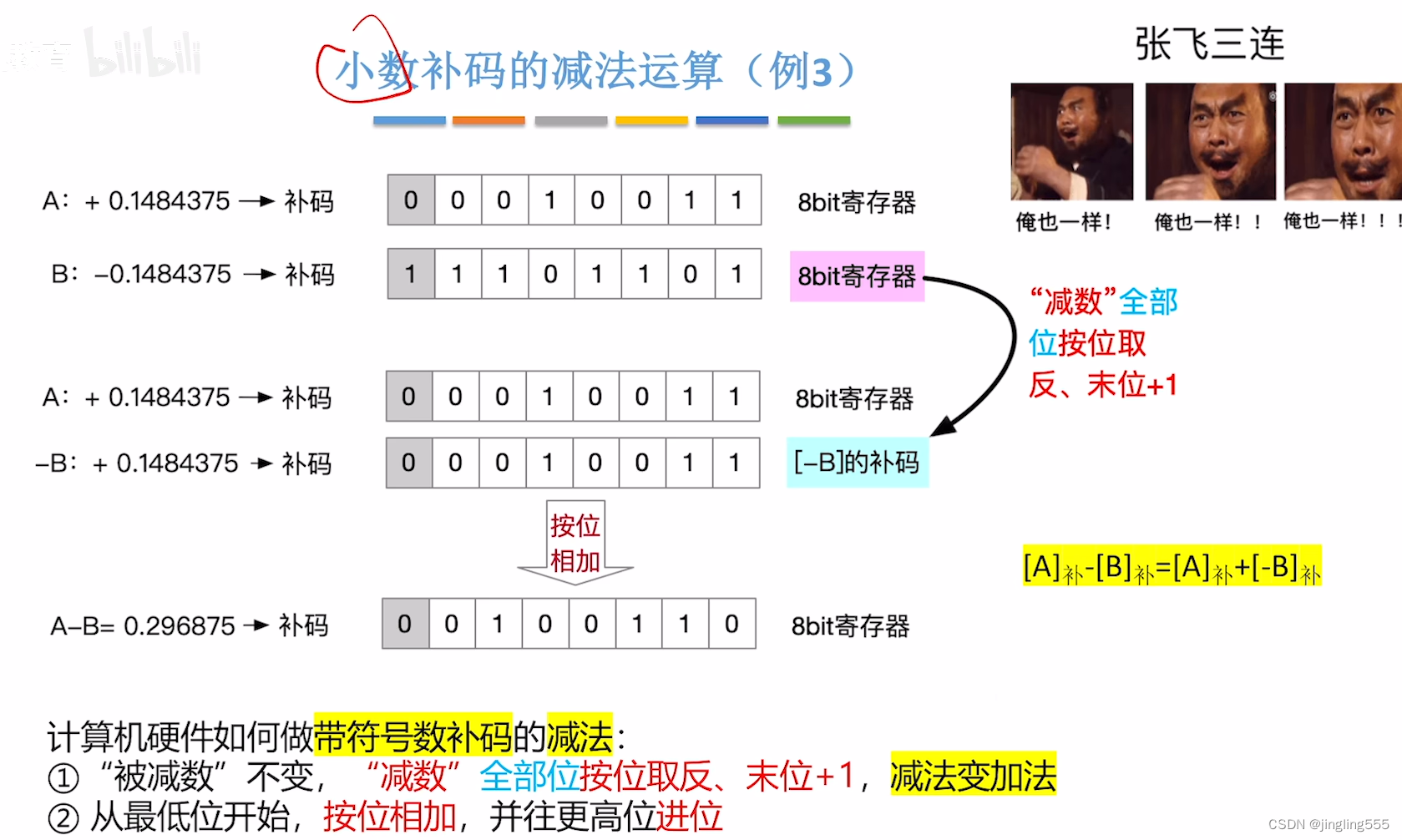
奇偶校验码
校验原理简介: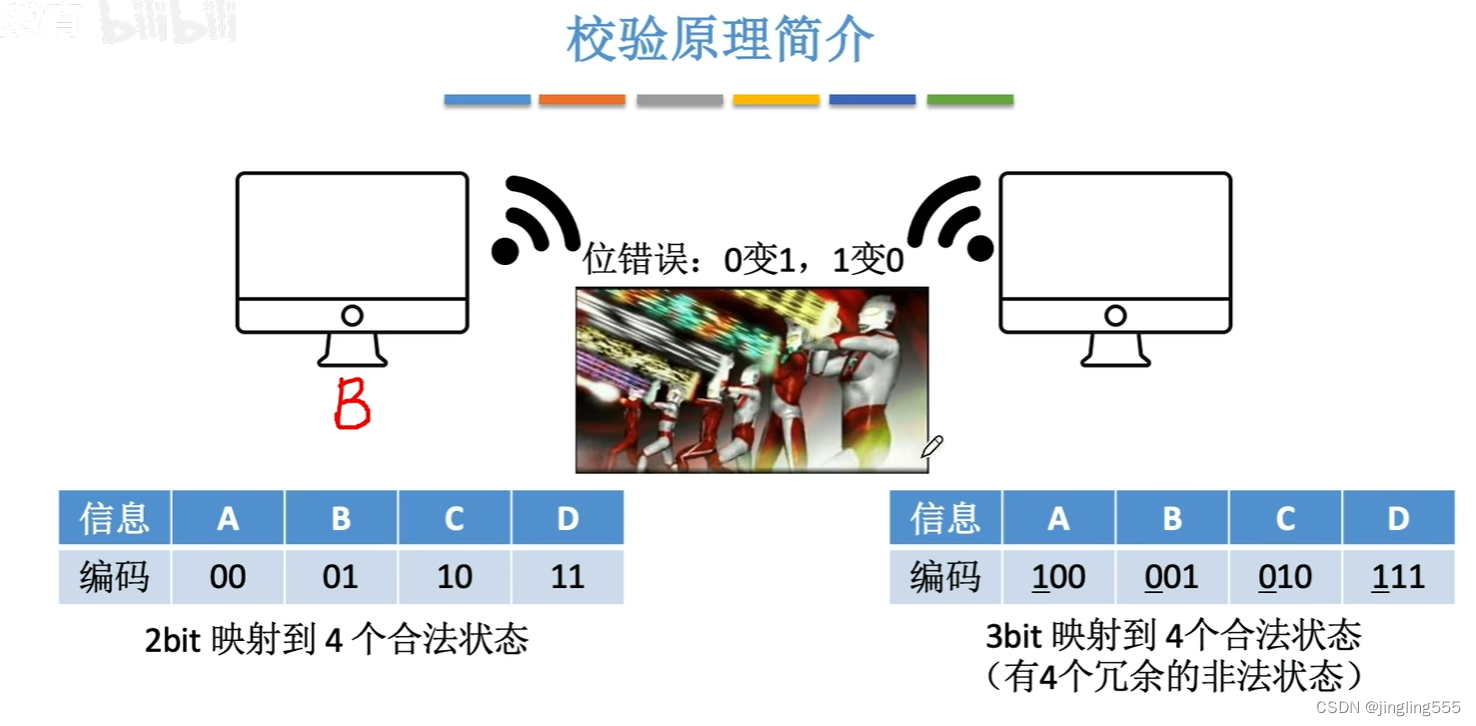
奇偶校验码: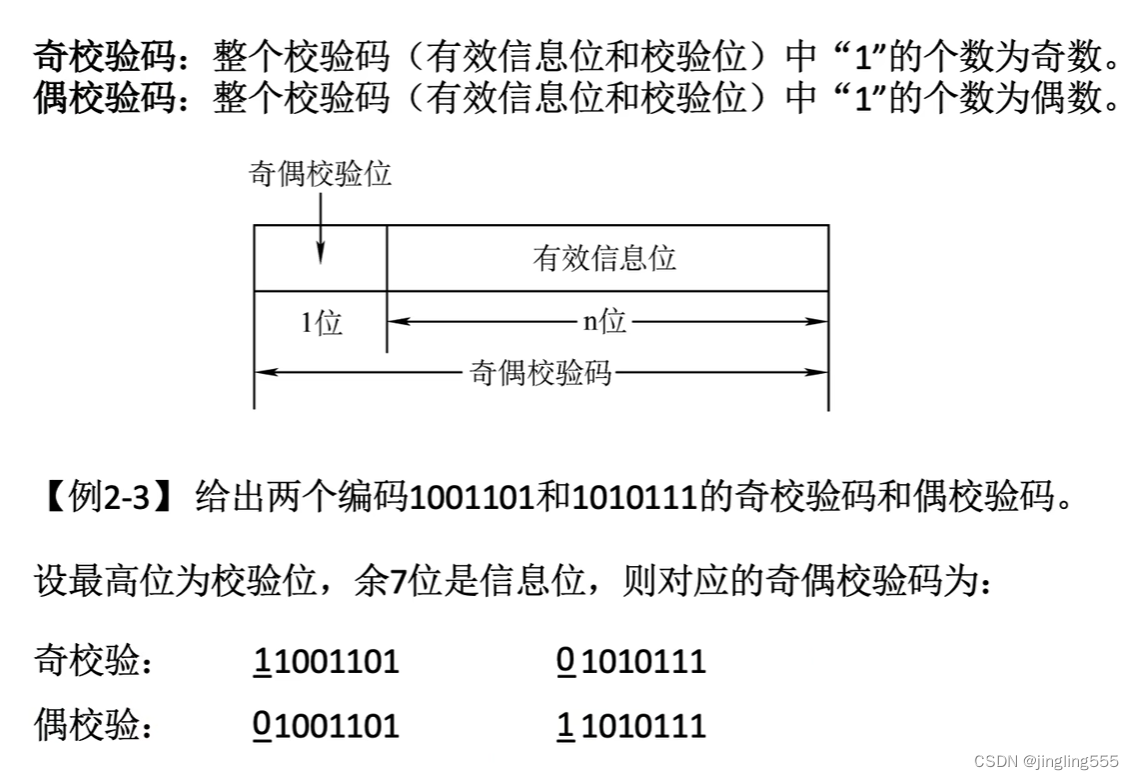
例题:
算数逻辑单元(电路基本原理&加法器设计)
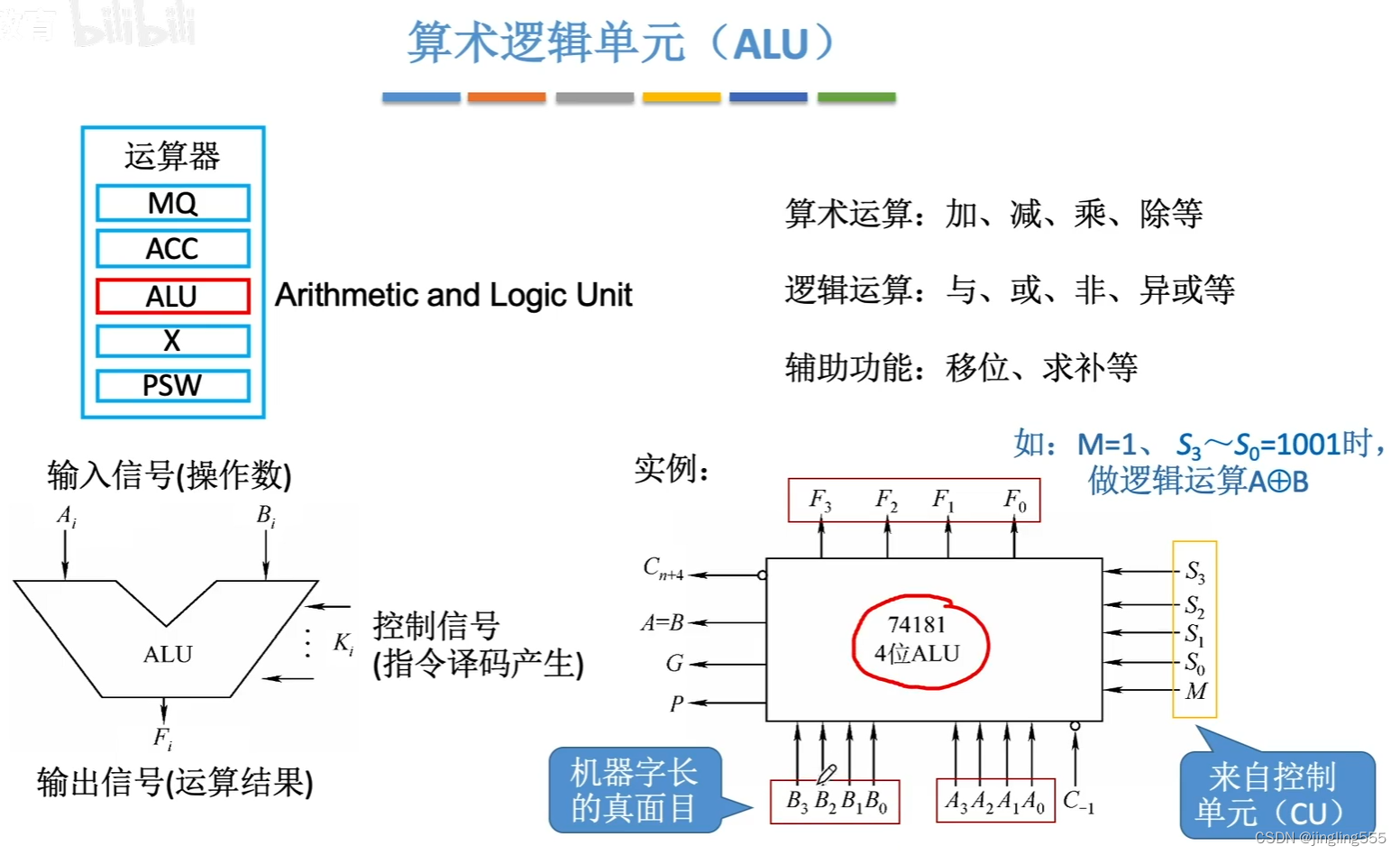
最基本的逻辑运算: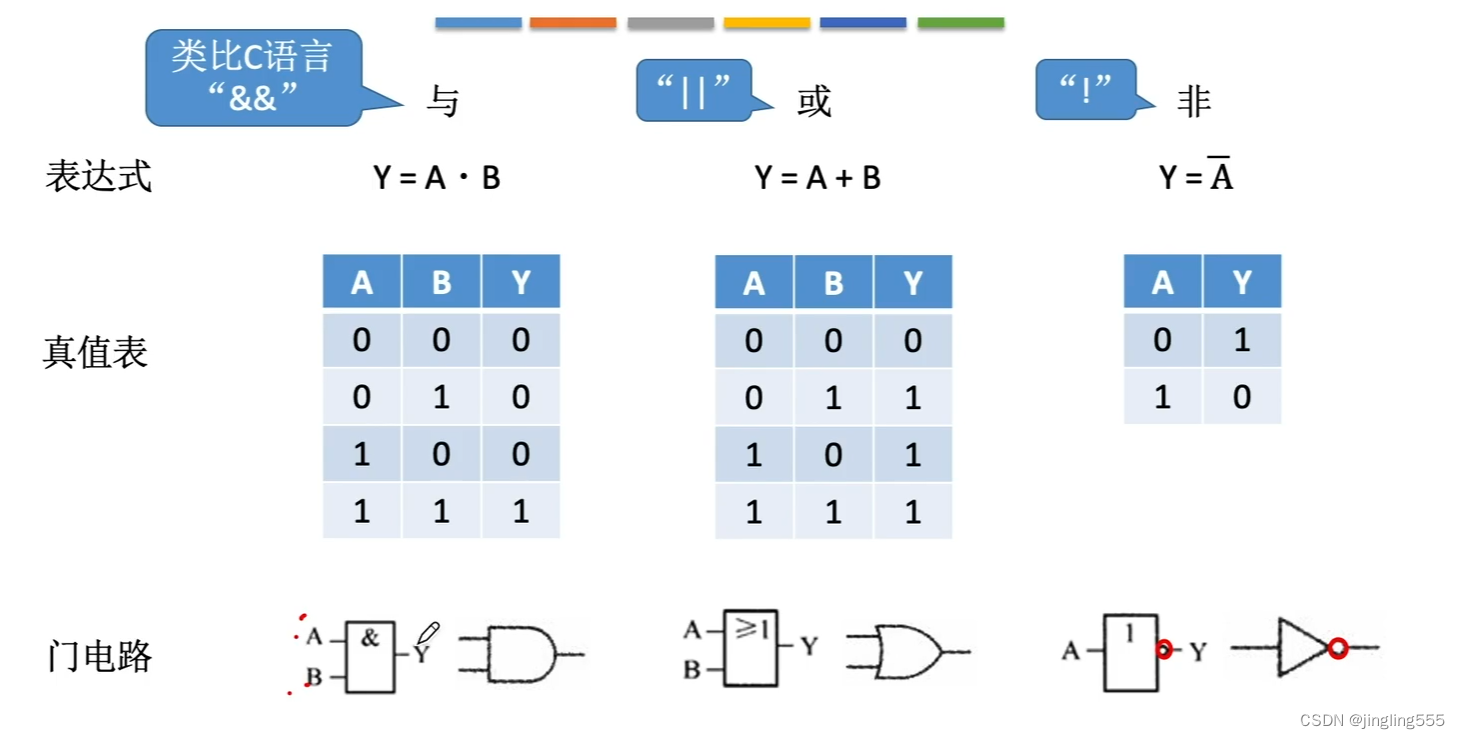
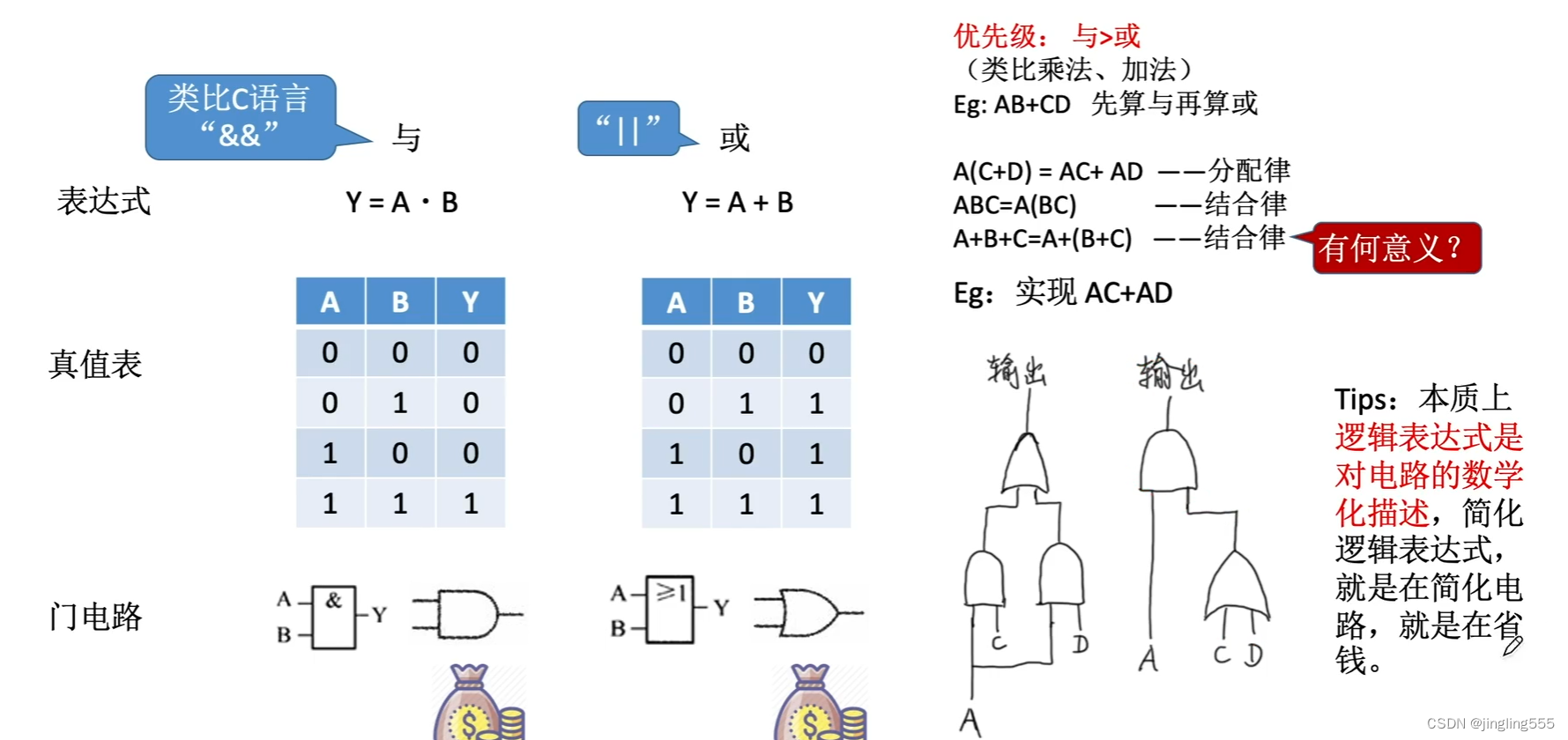
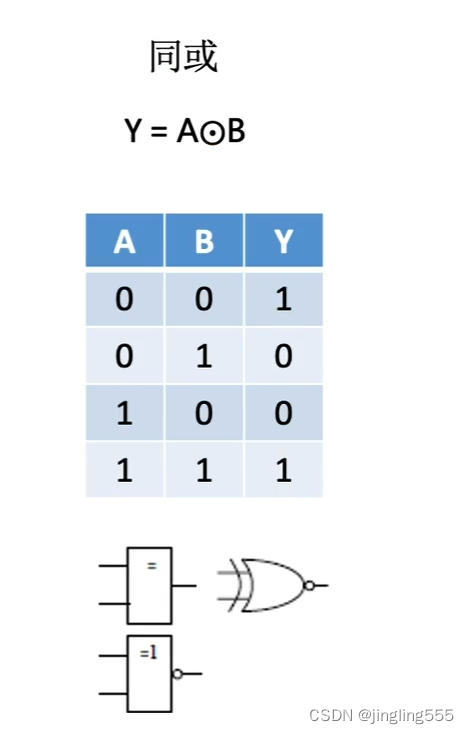
复合逻辑: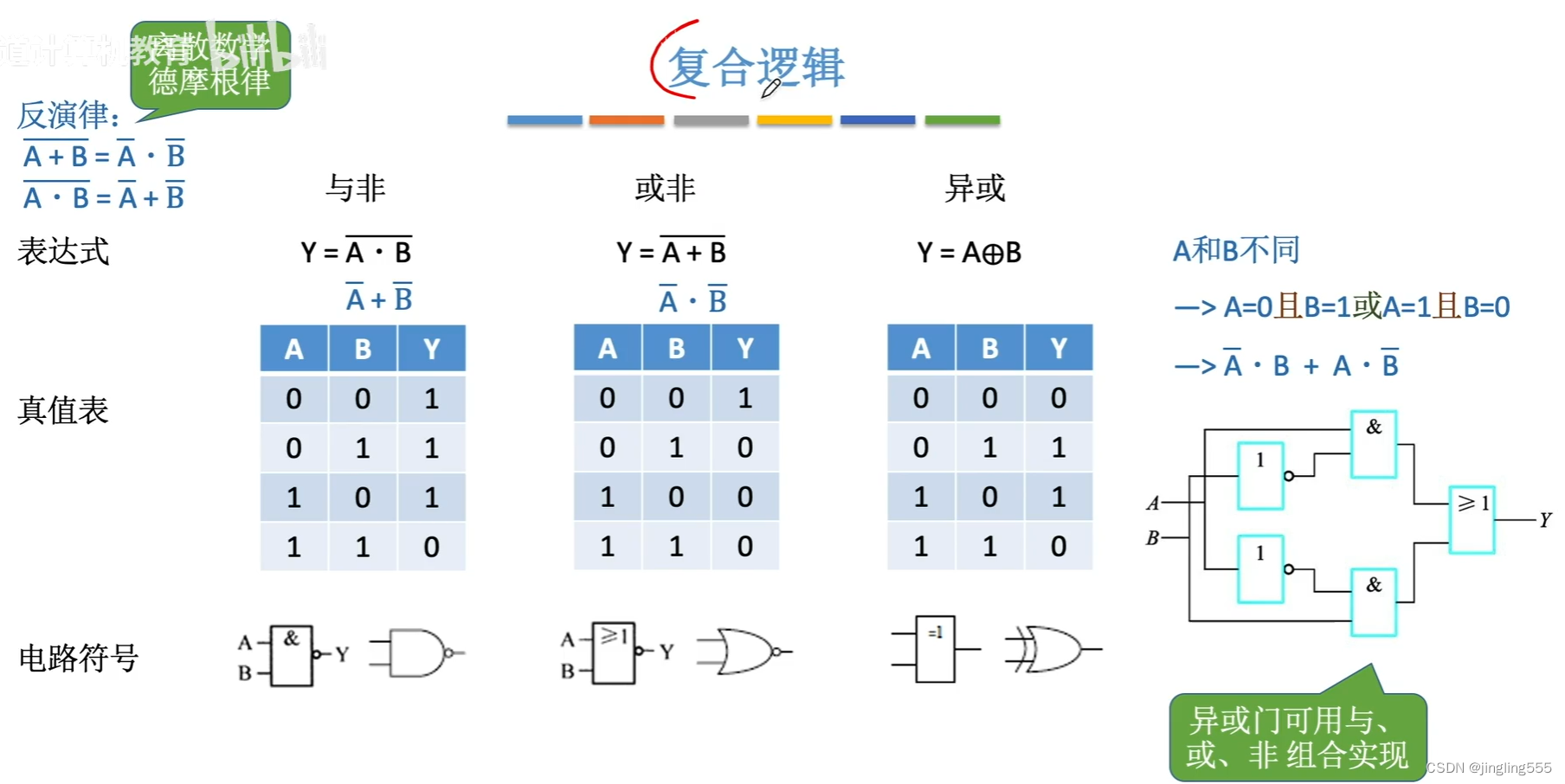
用门电路求偶校验位: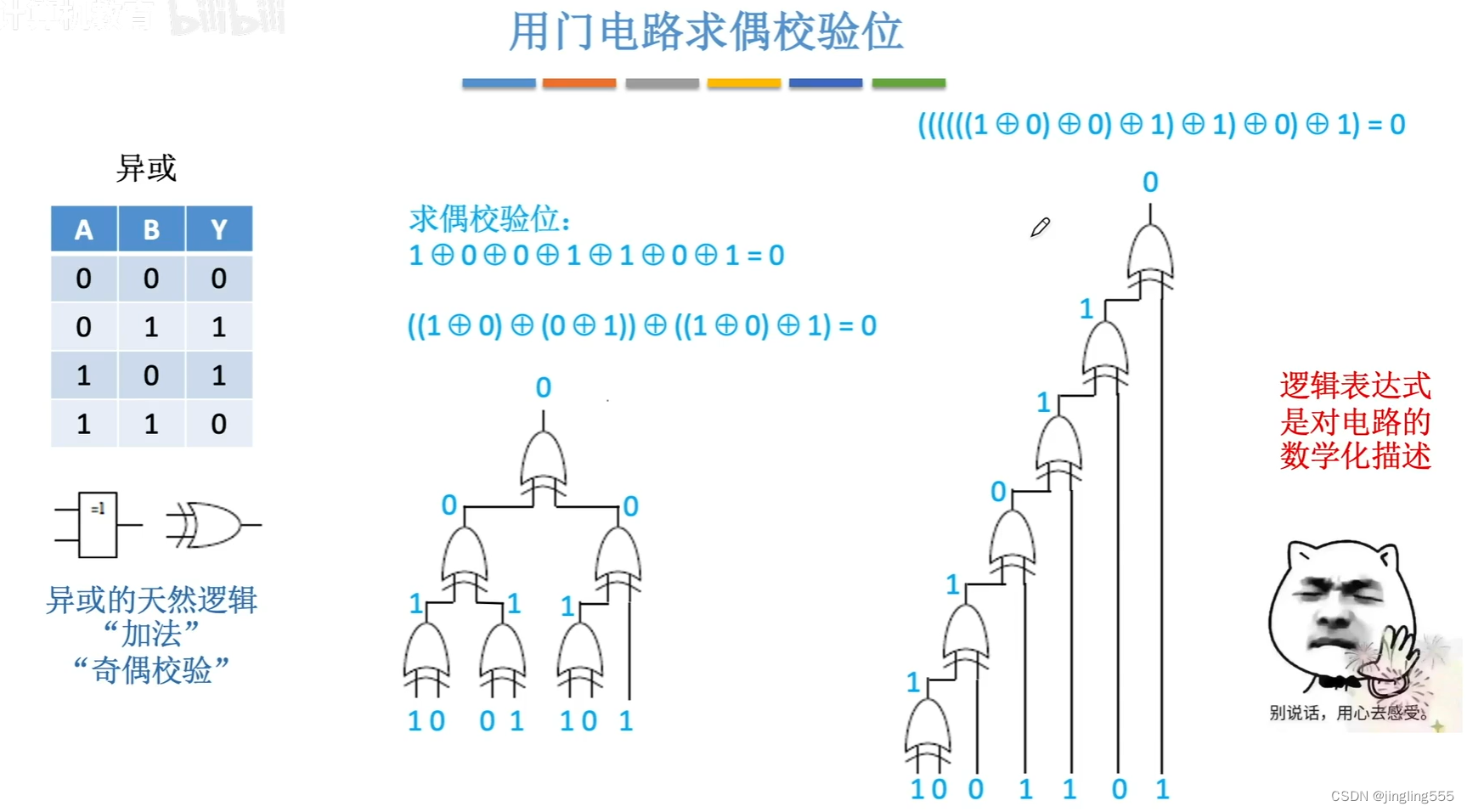
一位全加器: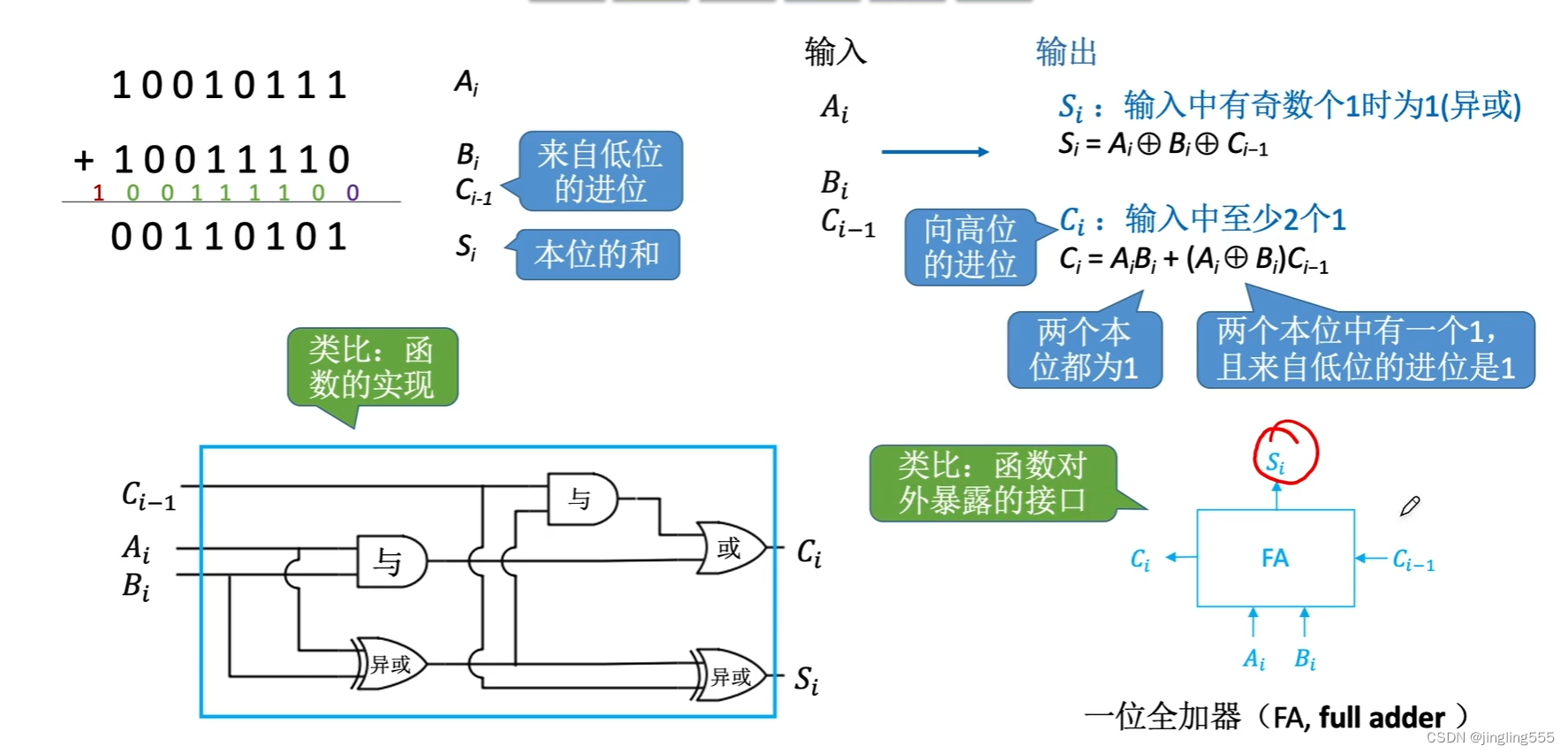
串行加法器: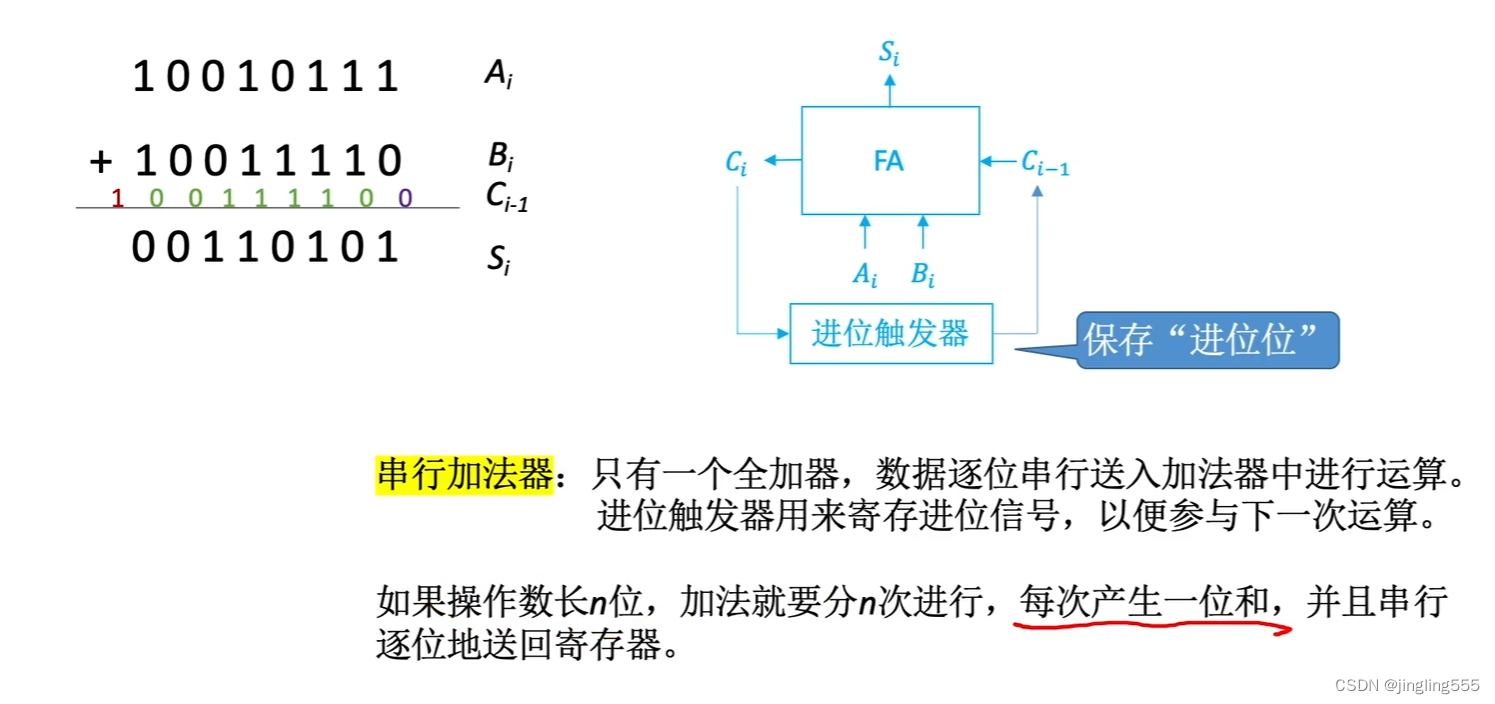
并行加法器: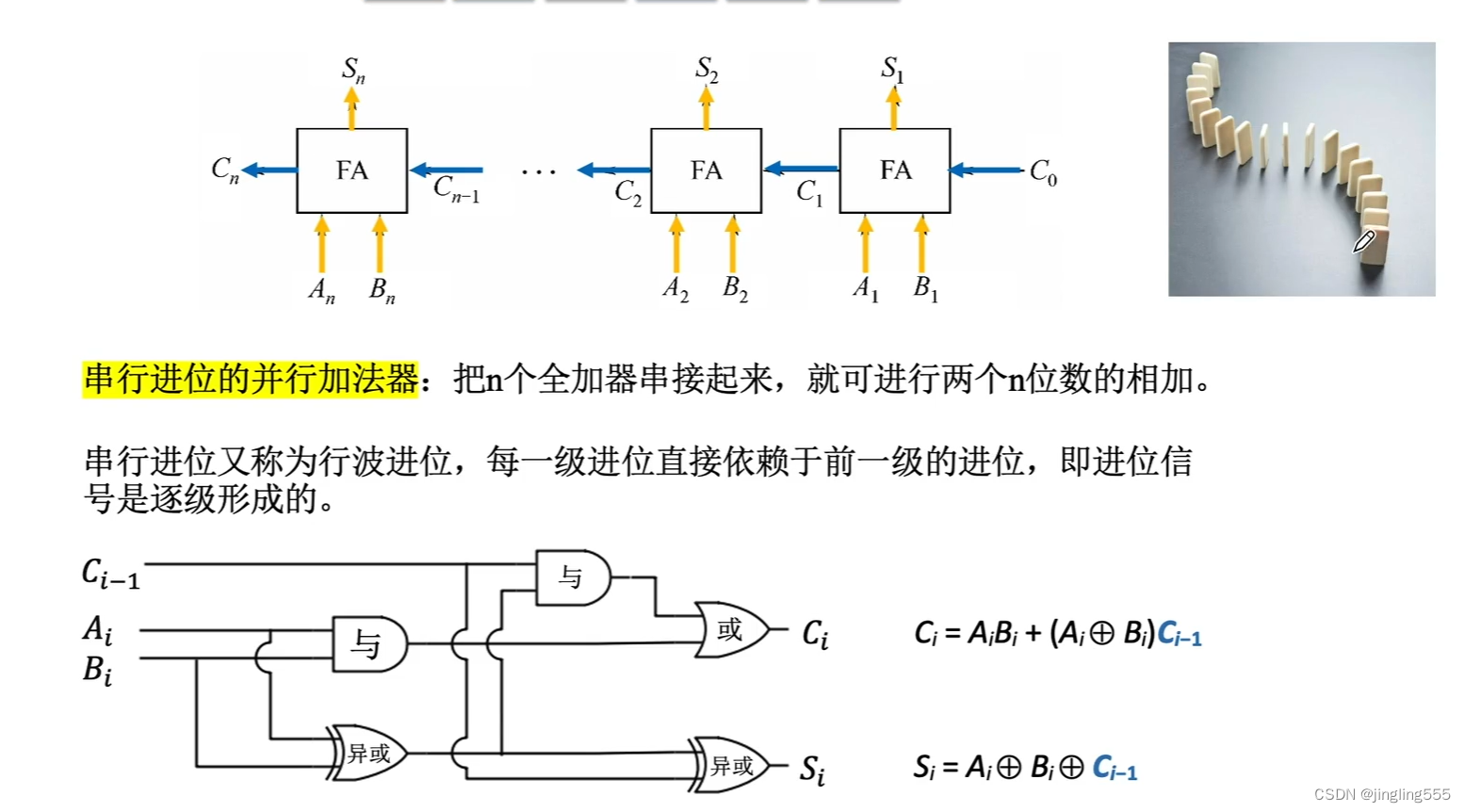
总结: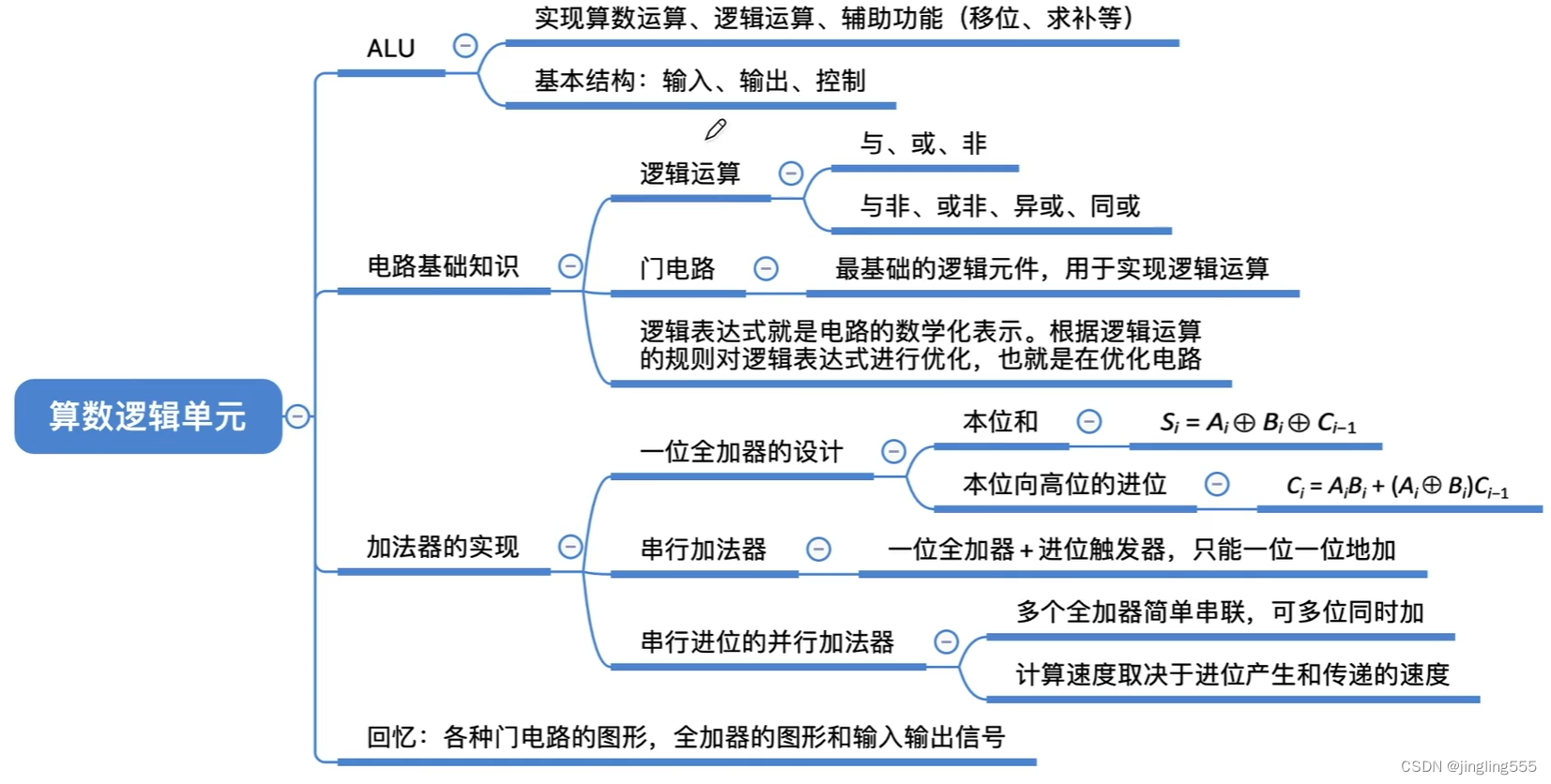
并行进位加法器
串行进位的并行加法器: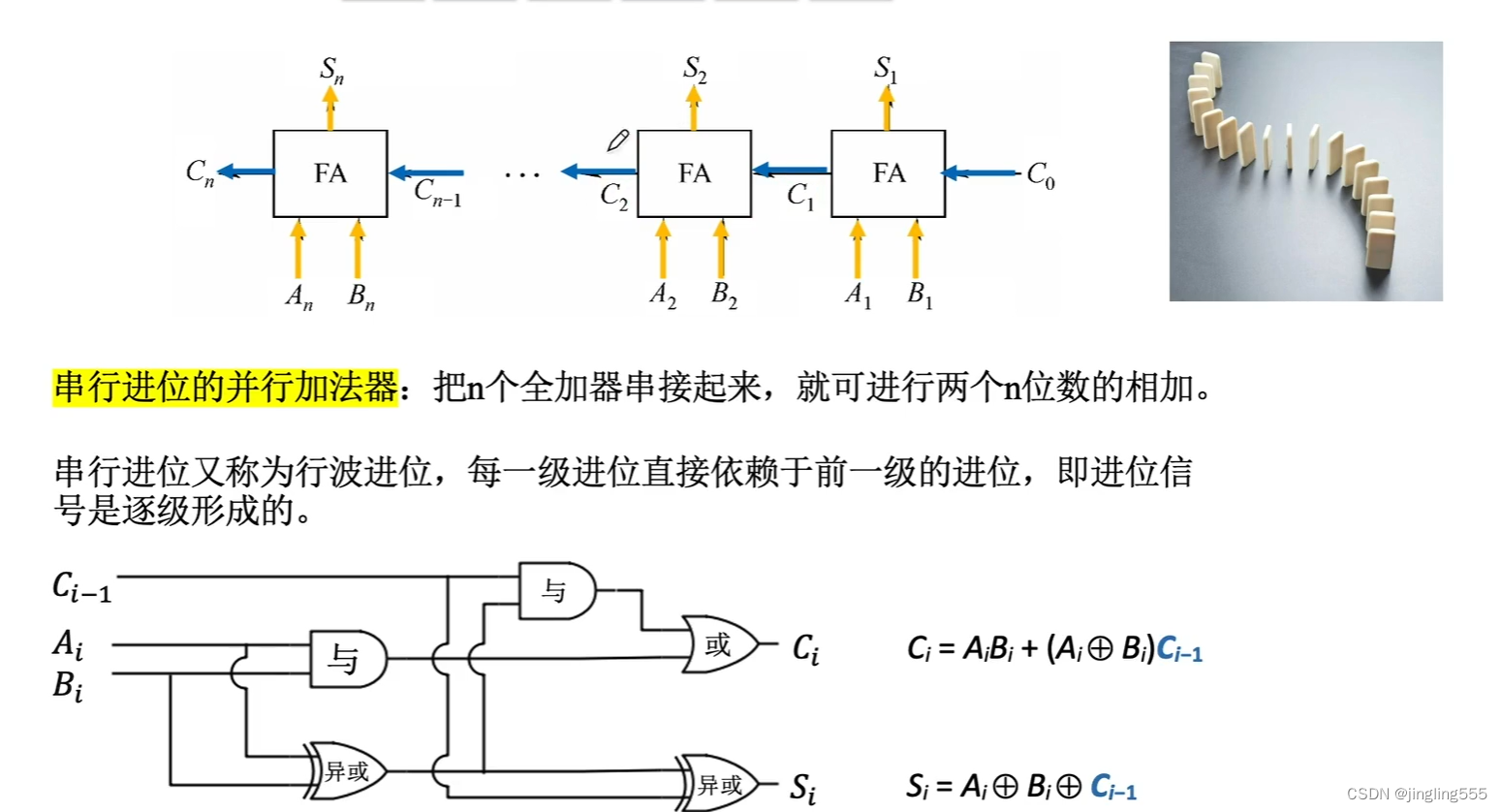
如何更快的产生进位?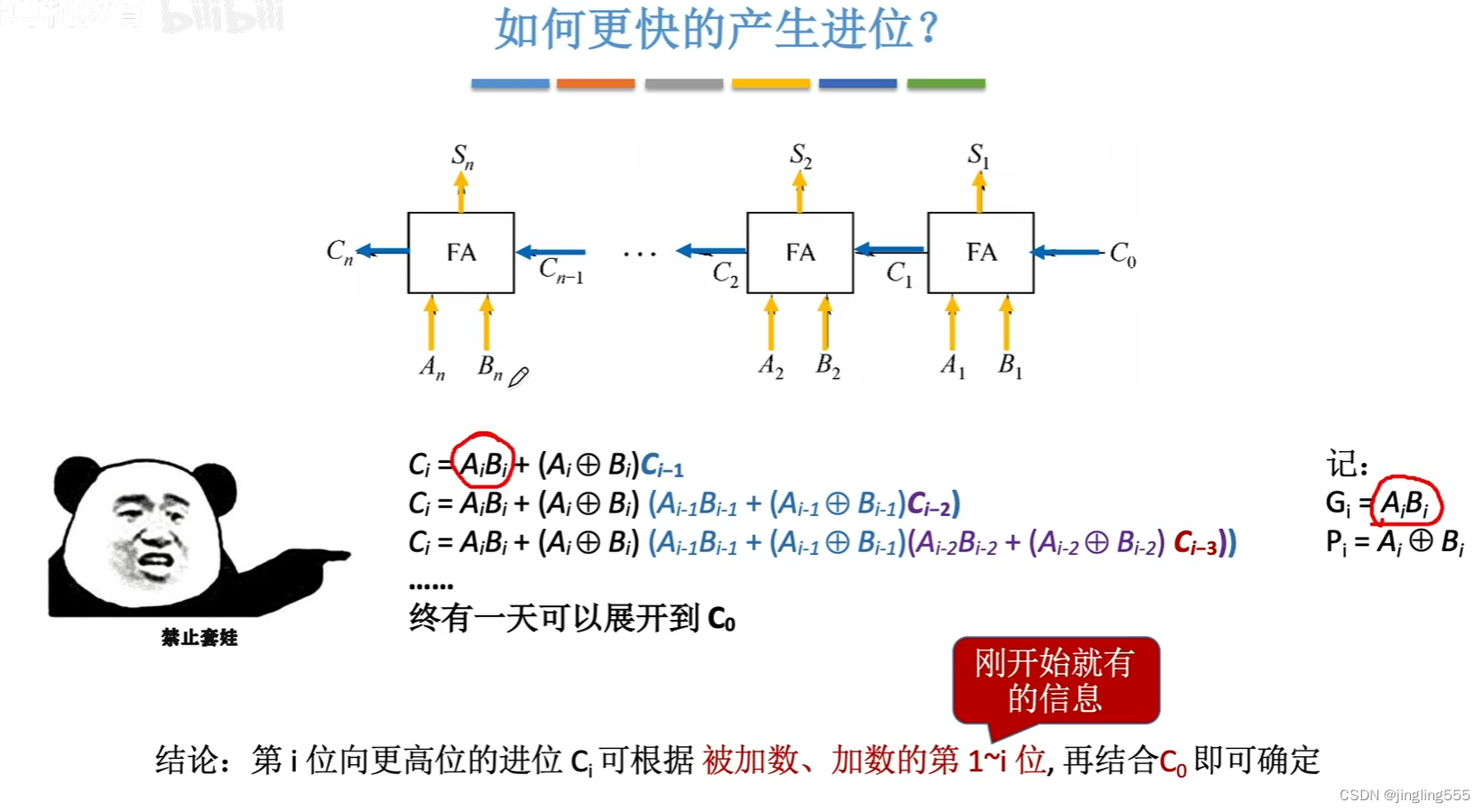
并行加法器的优化: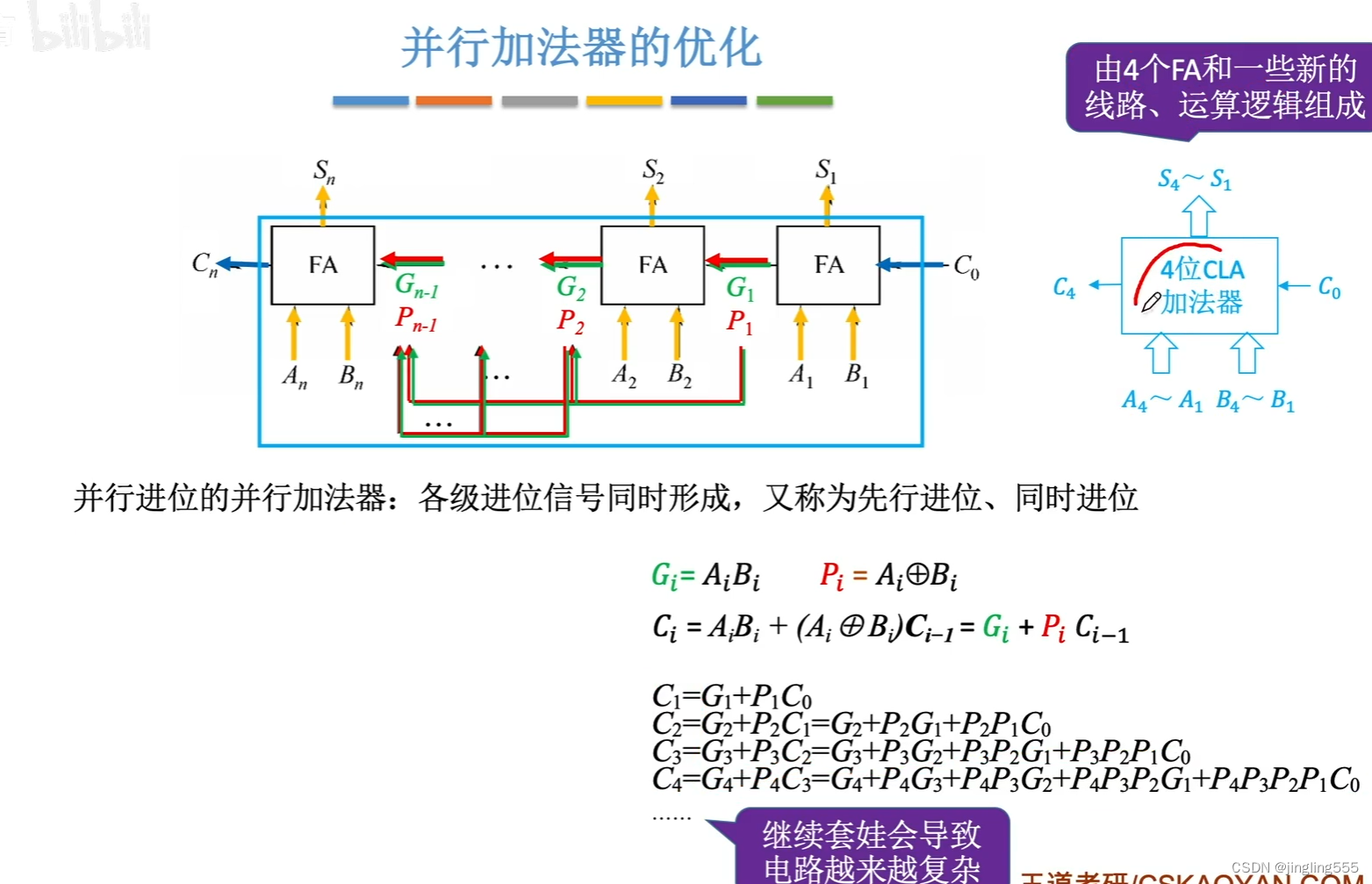
补码加减运算器
加法器原理:
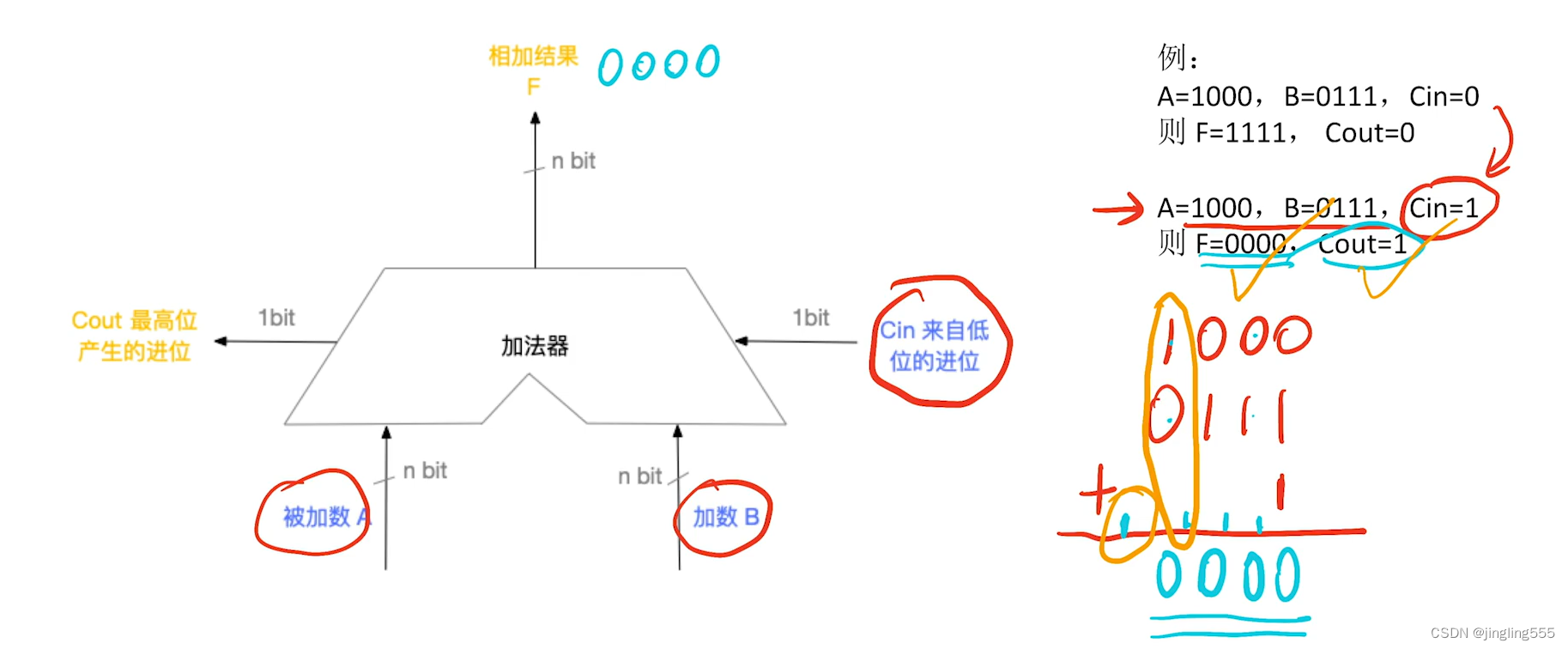
补码加/减法运算方法:
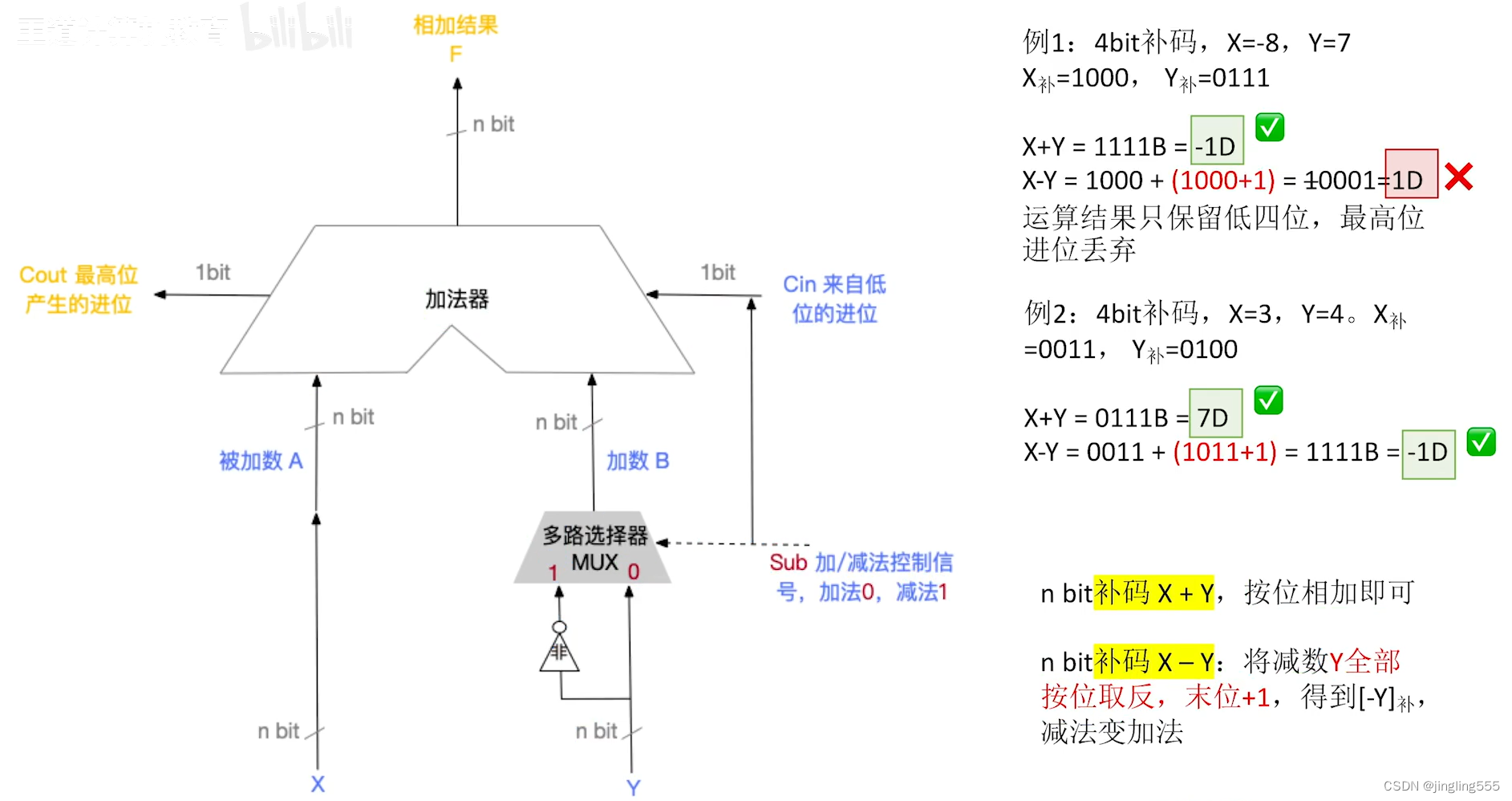
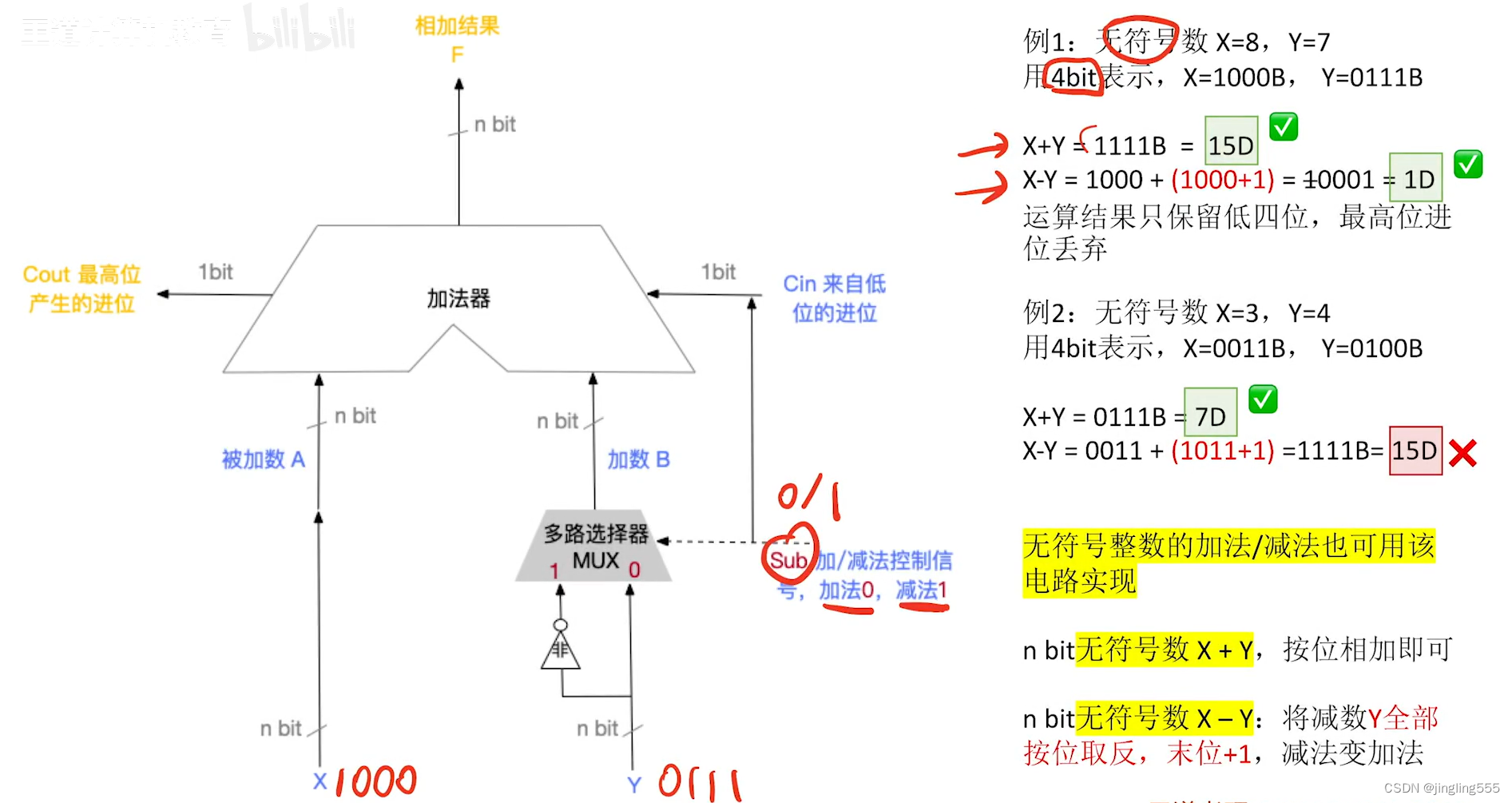
加减运算&溢出判断
原码的加减运算: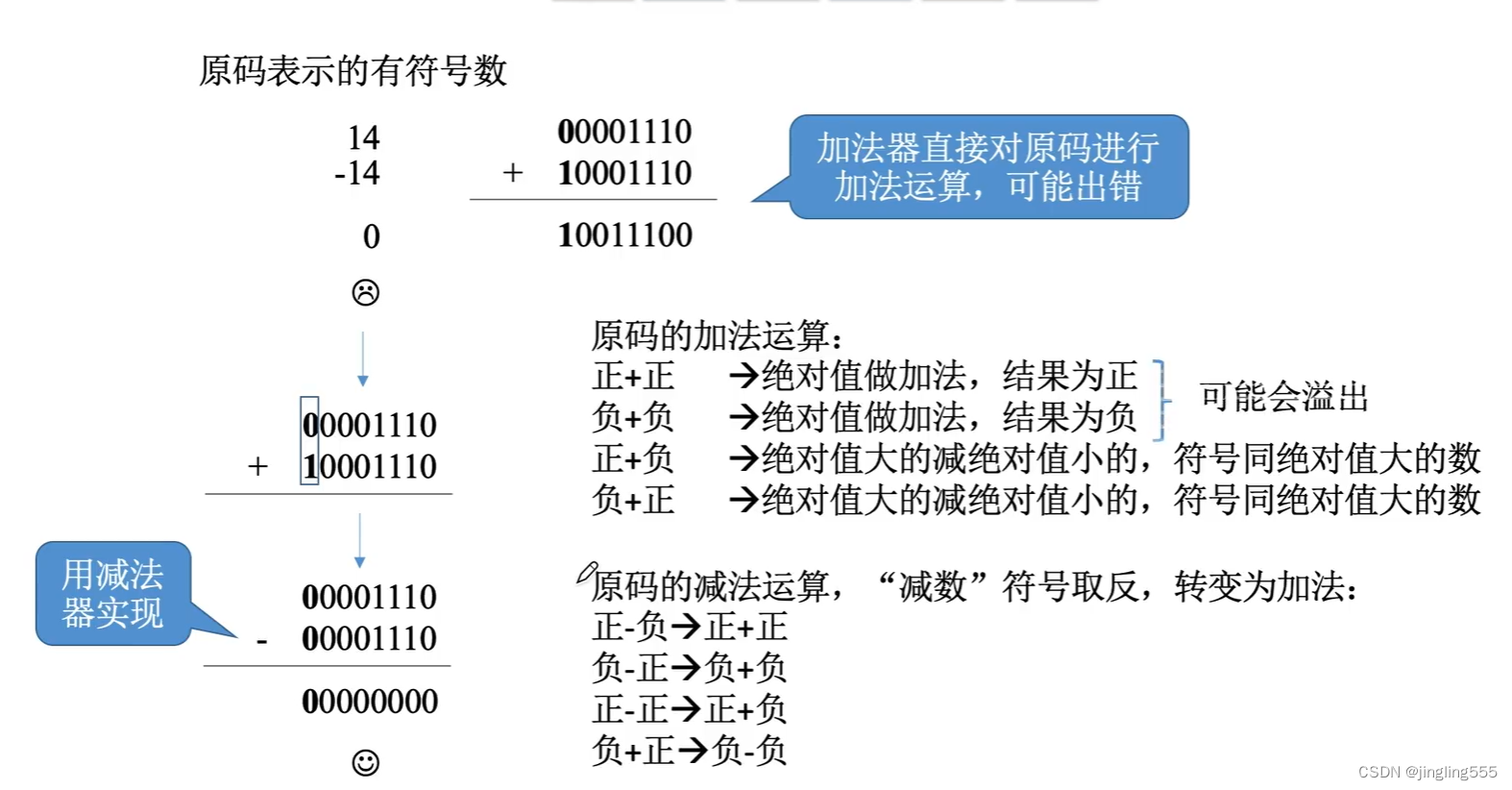
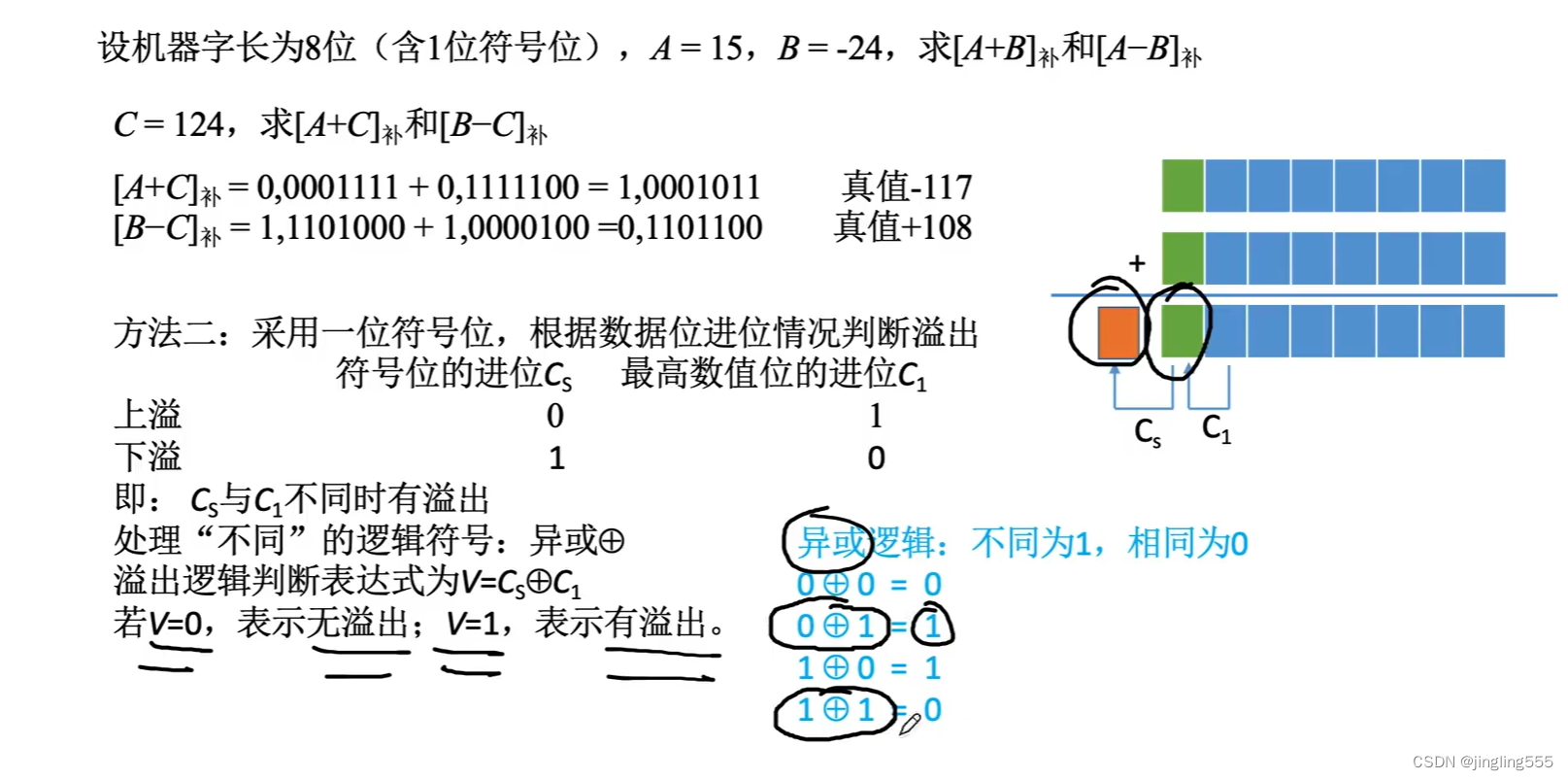
补码的加减运算:
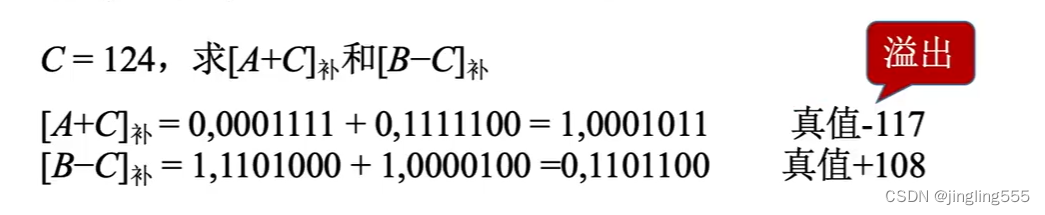
溢出判断:


符号扩展: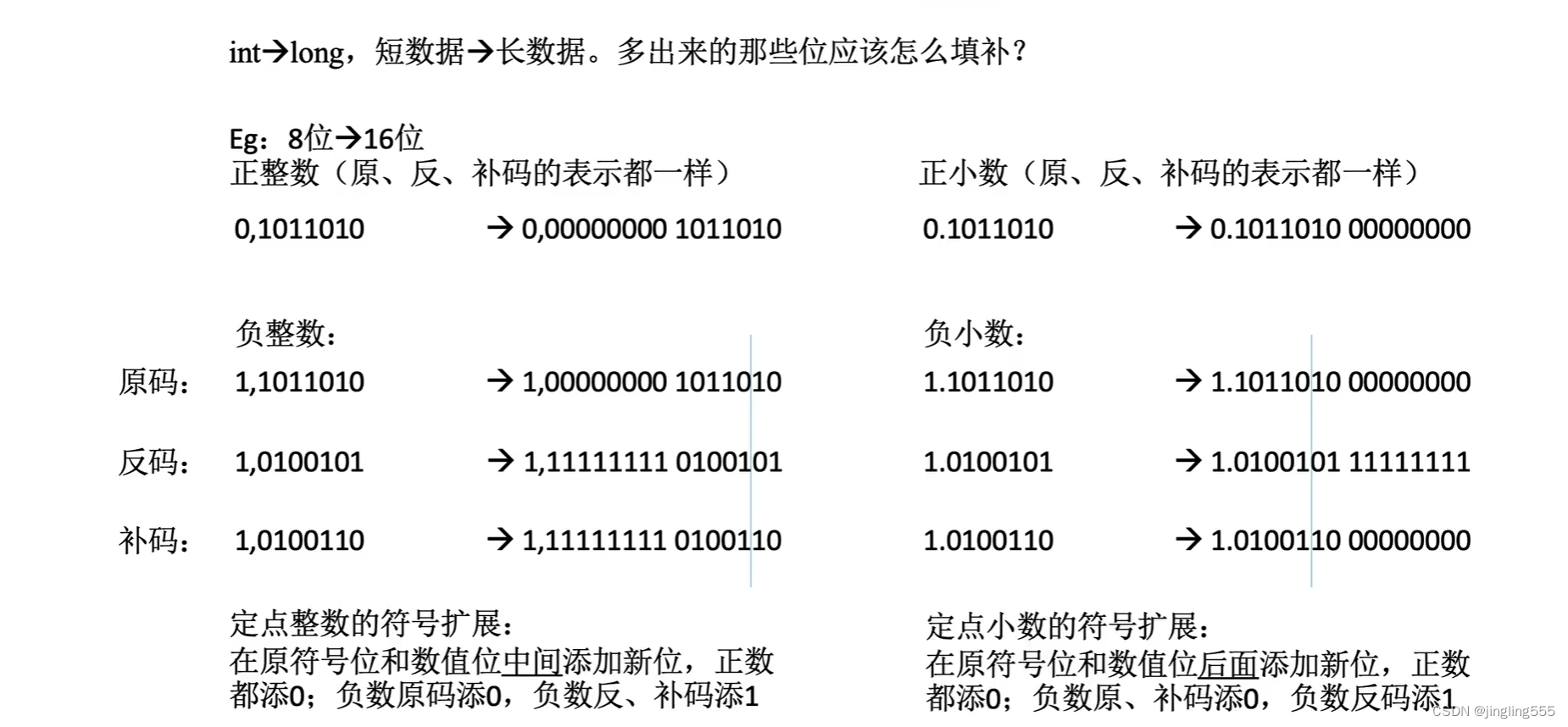
总结: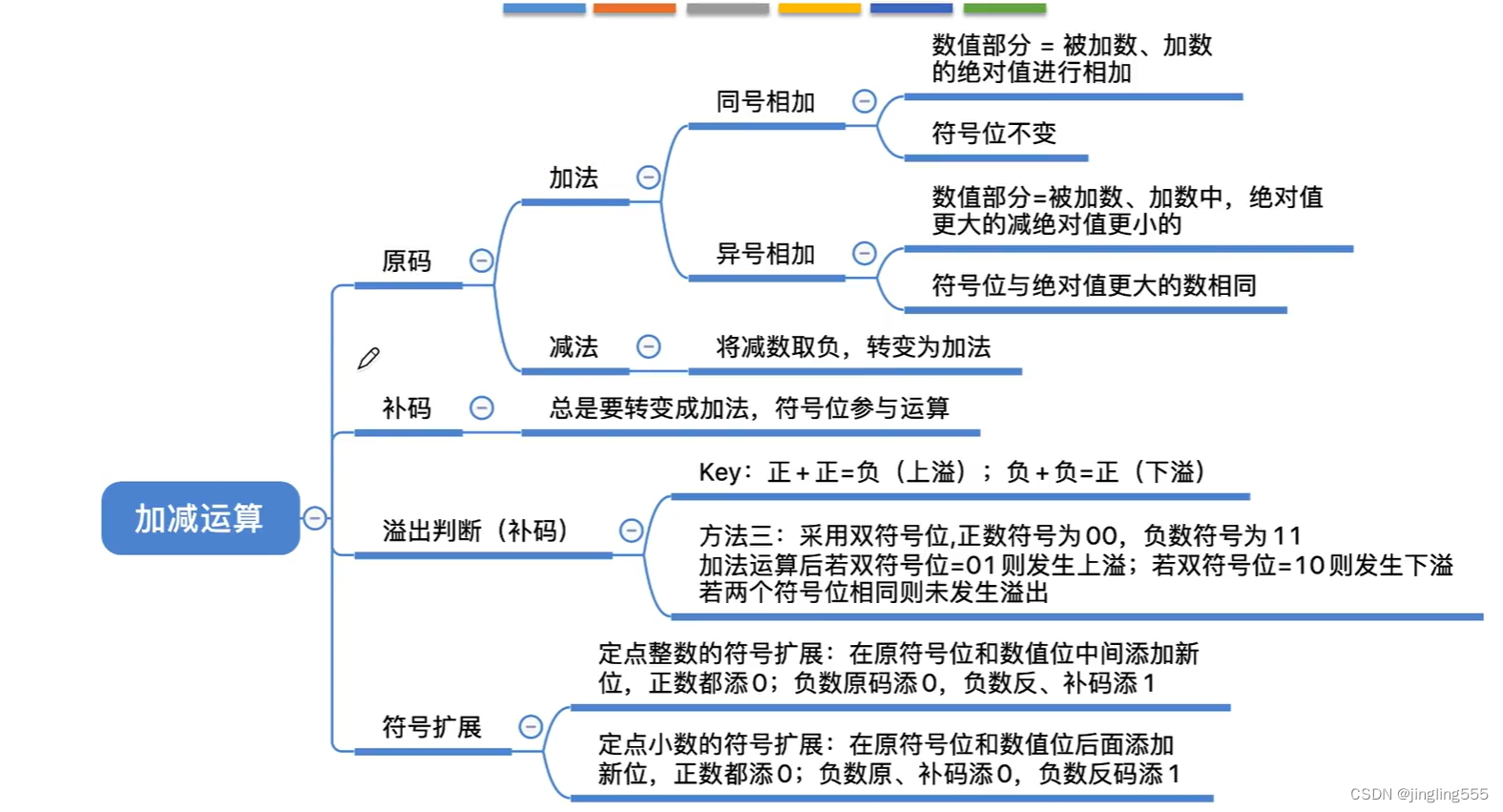
标志位的生成
OF: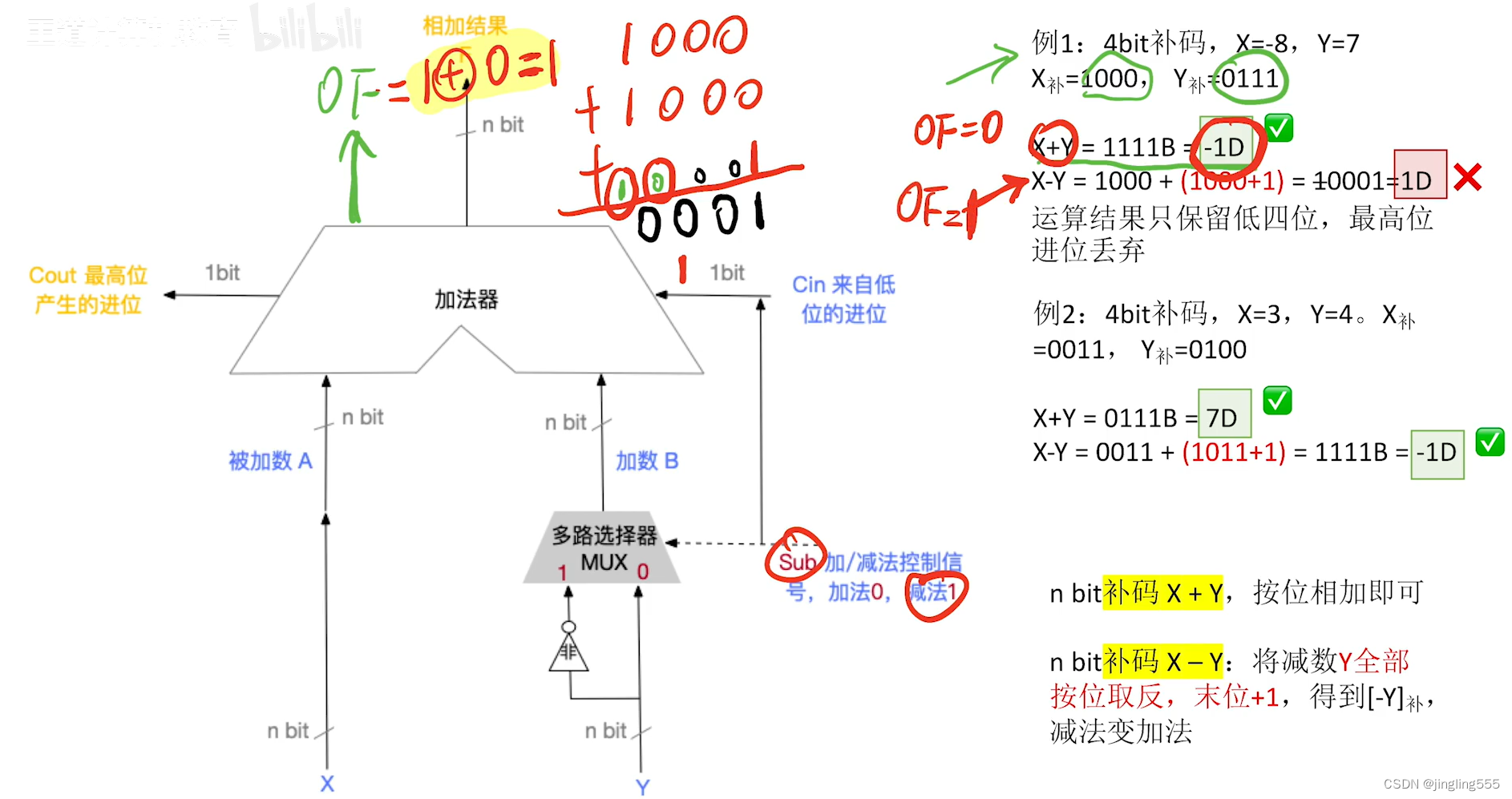
SF,ZF,CF: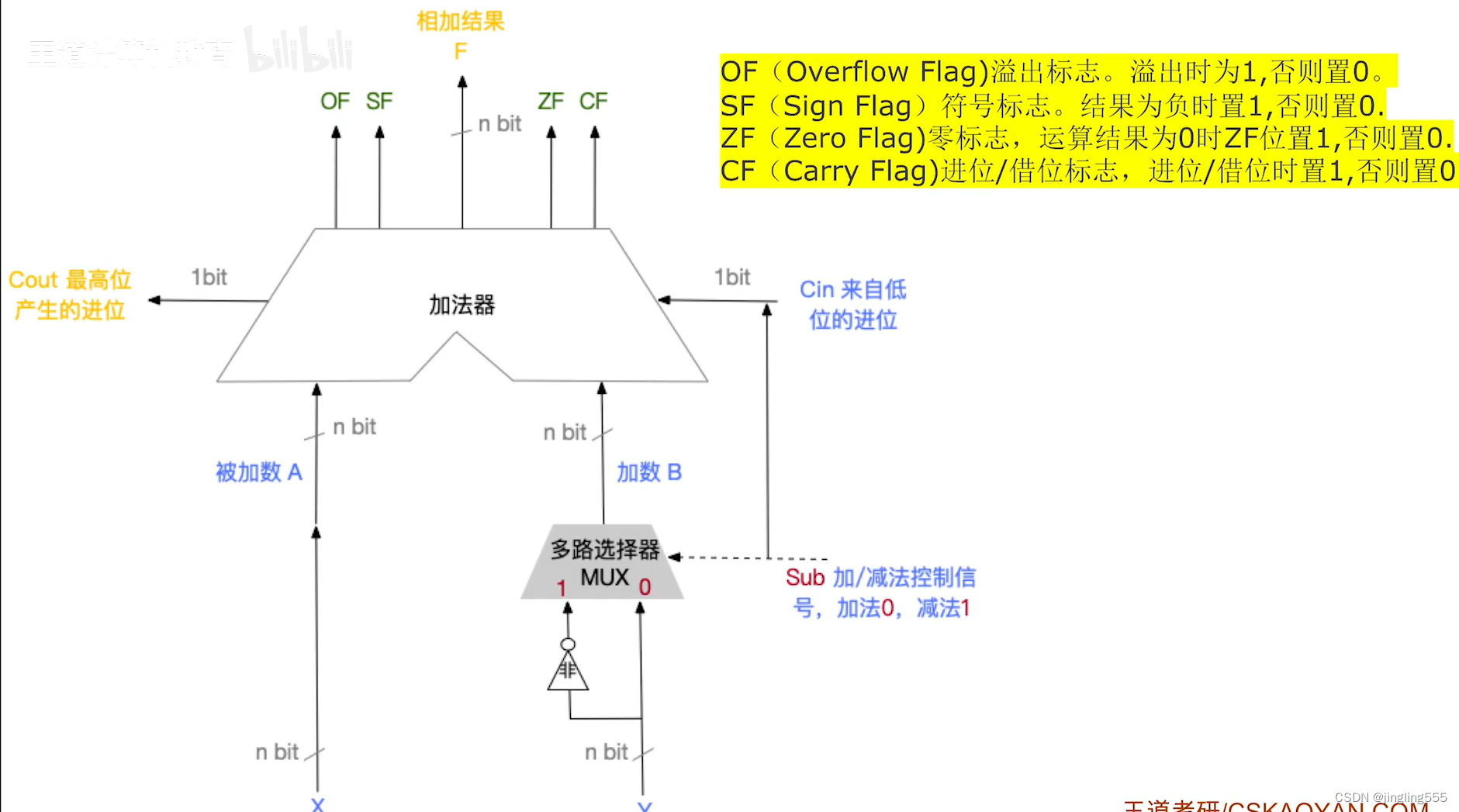
总结: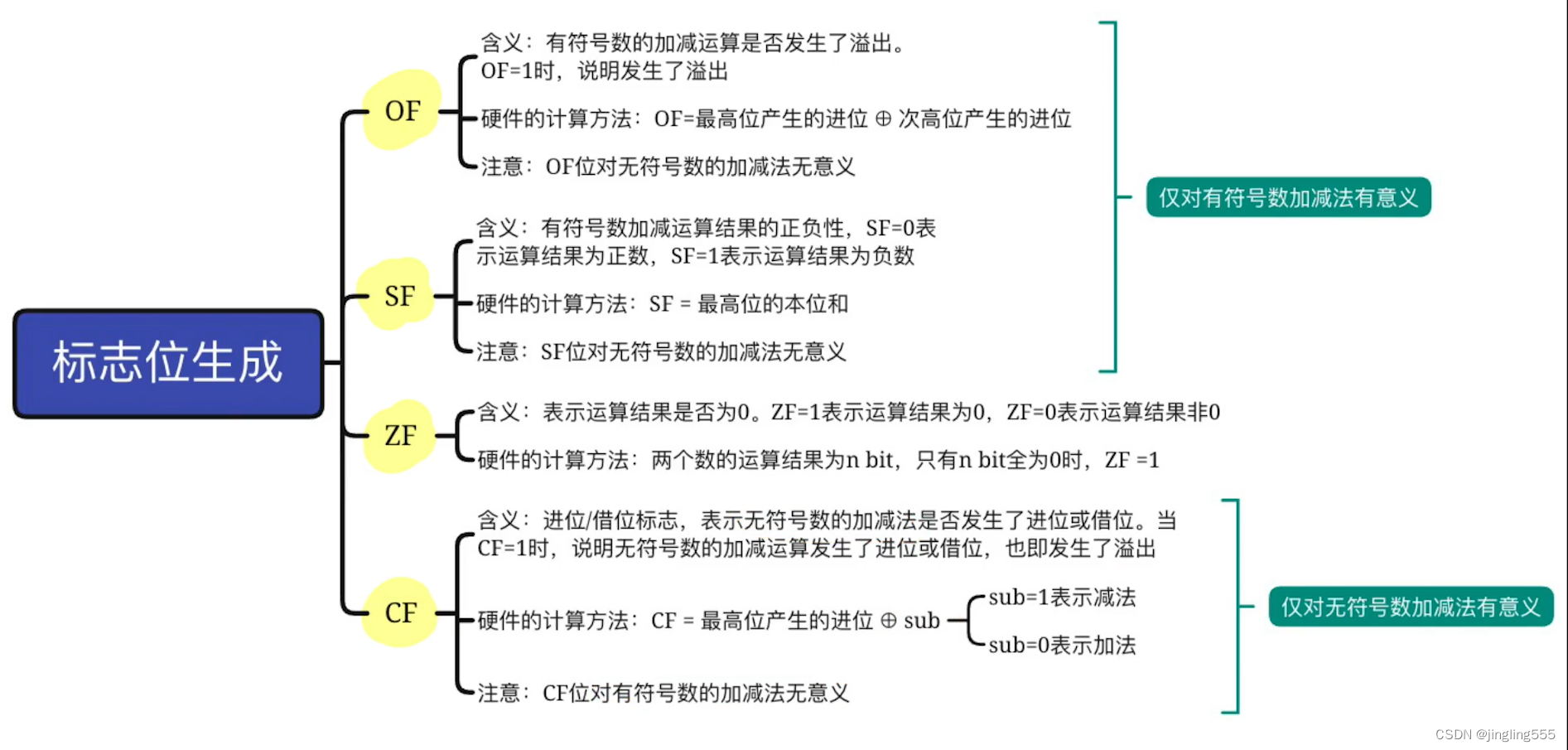
定点数的移位运算
算数移位:
原码的算数移位: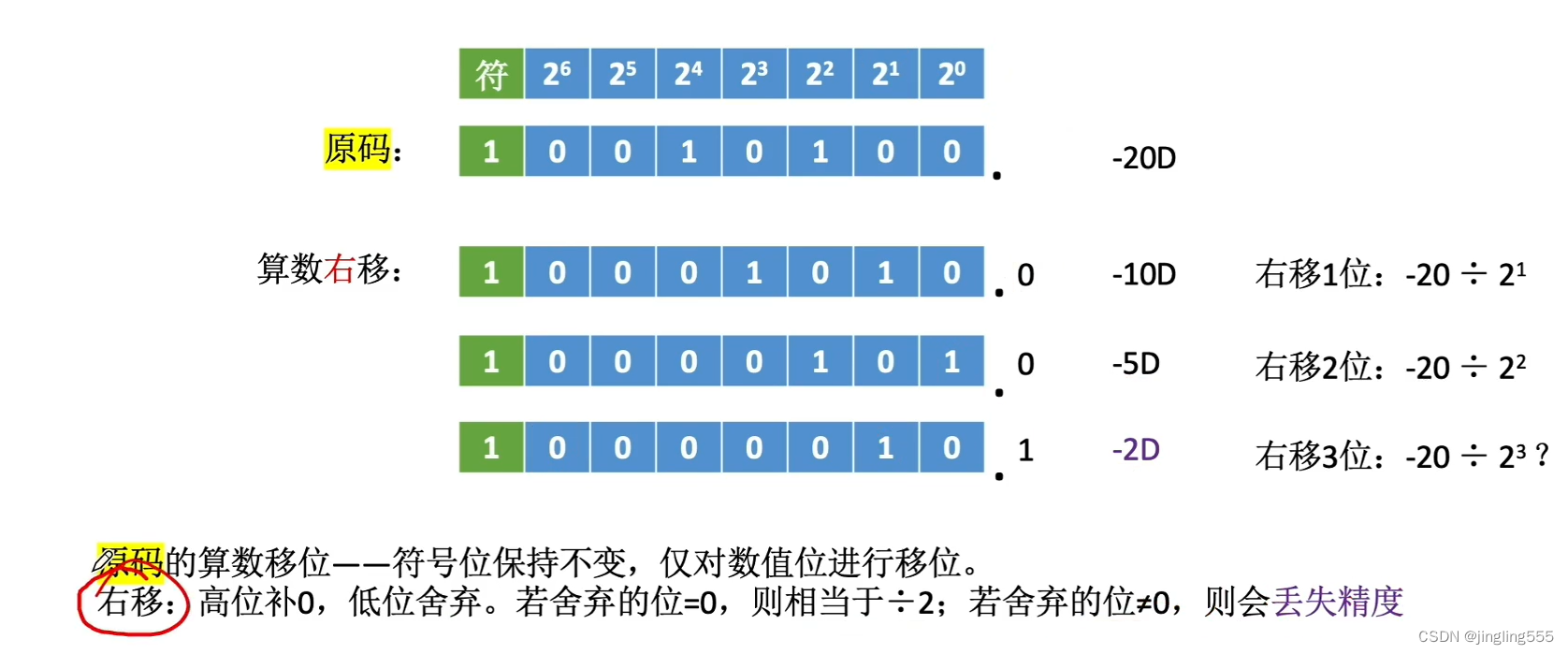
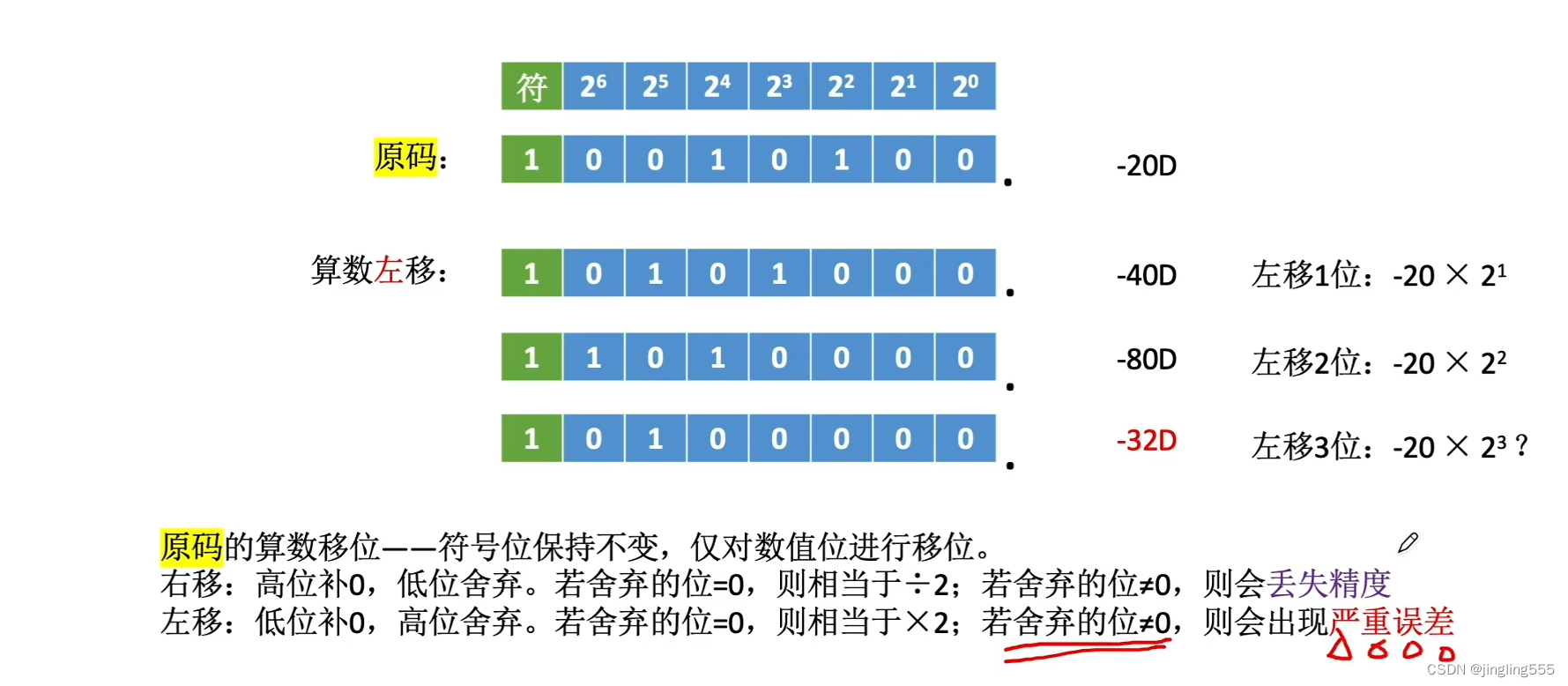
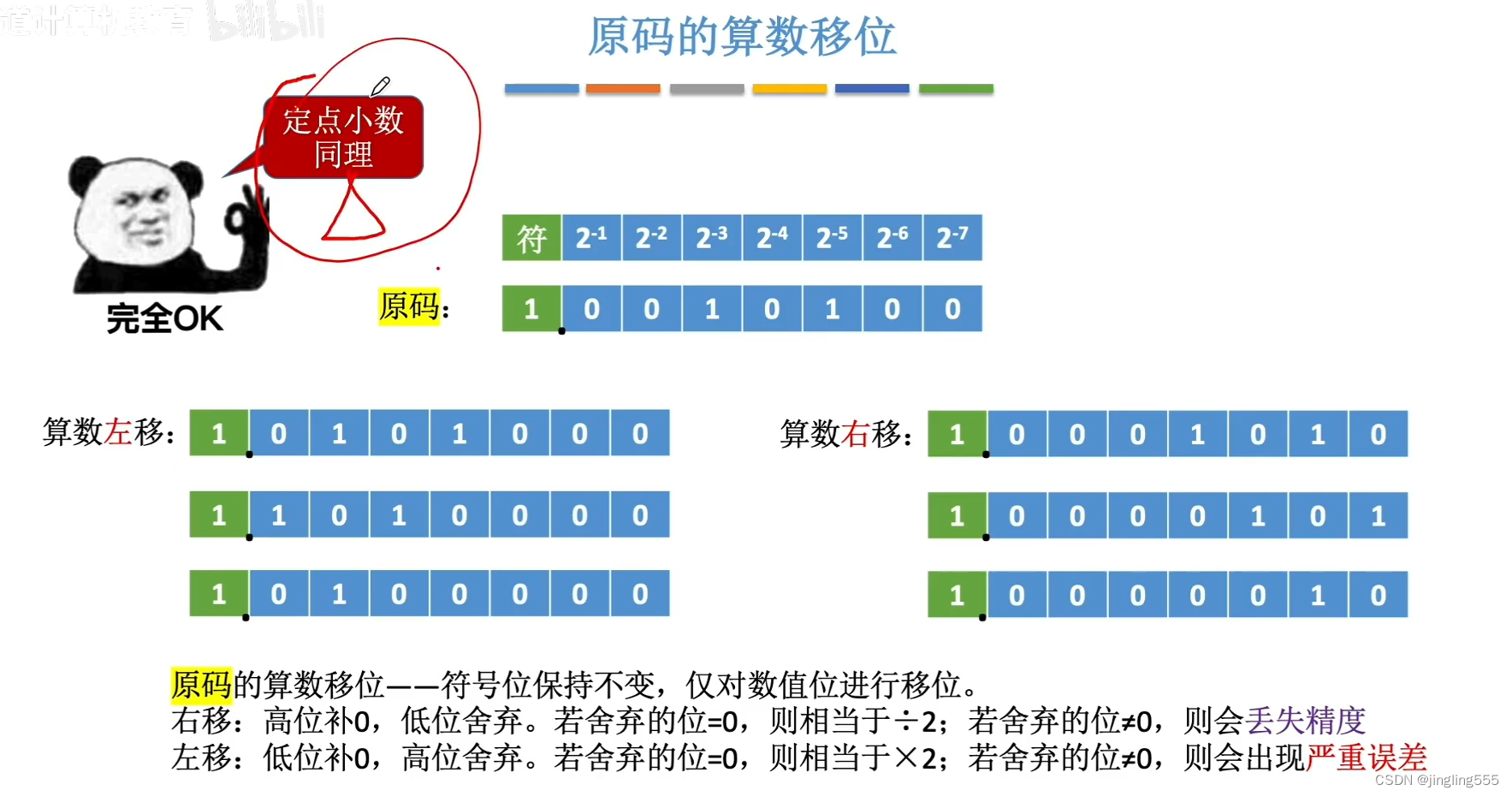
反码的算数移位: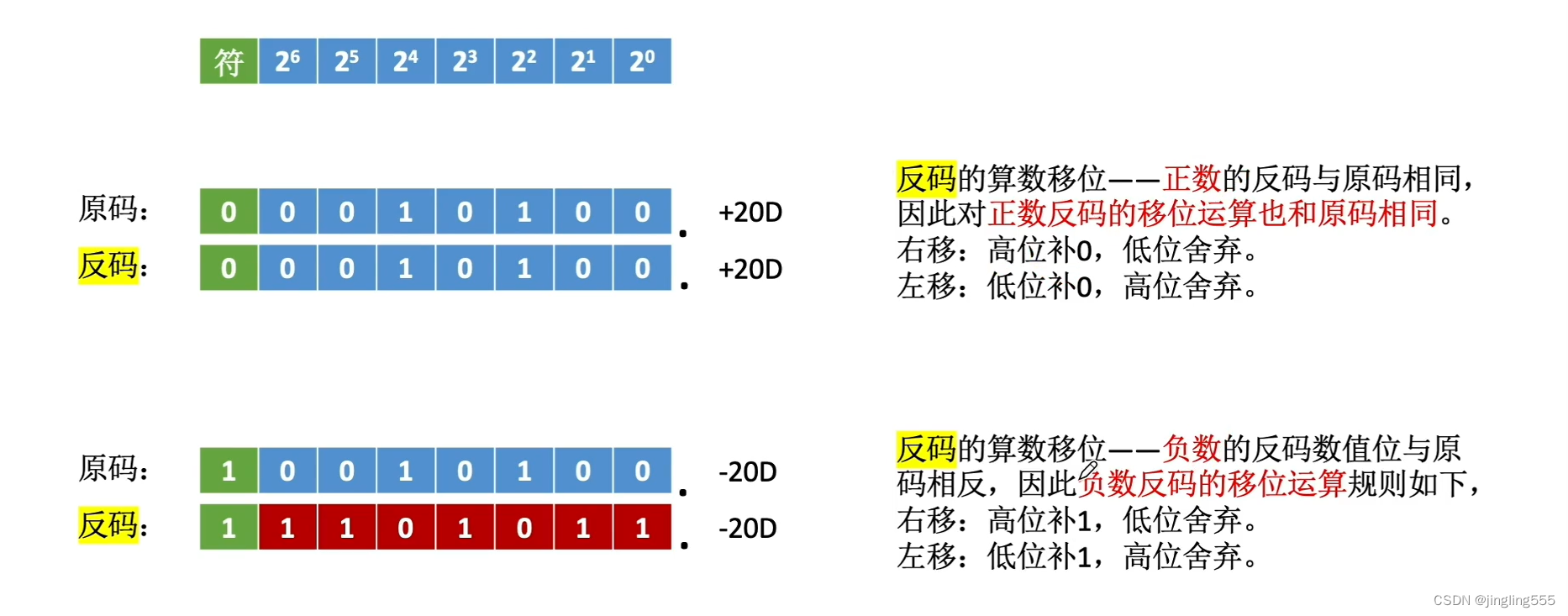
补码的算数移位: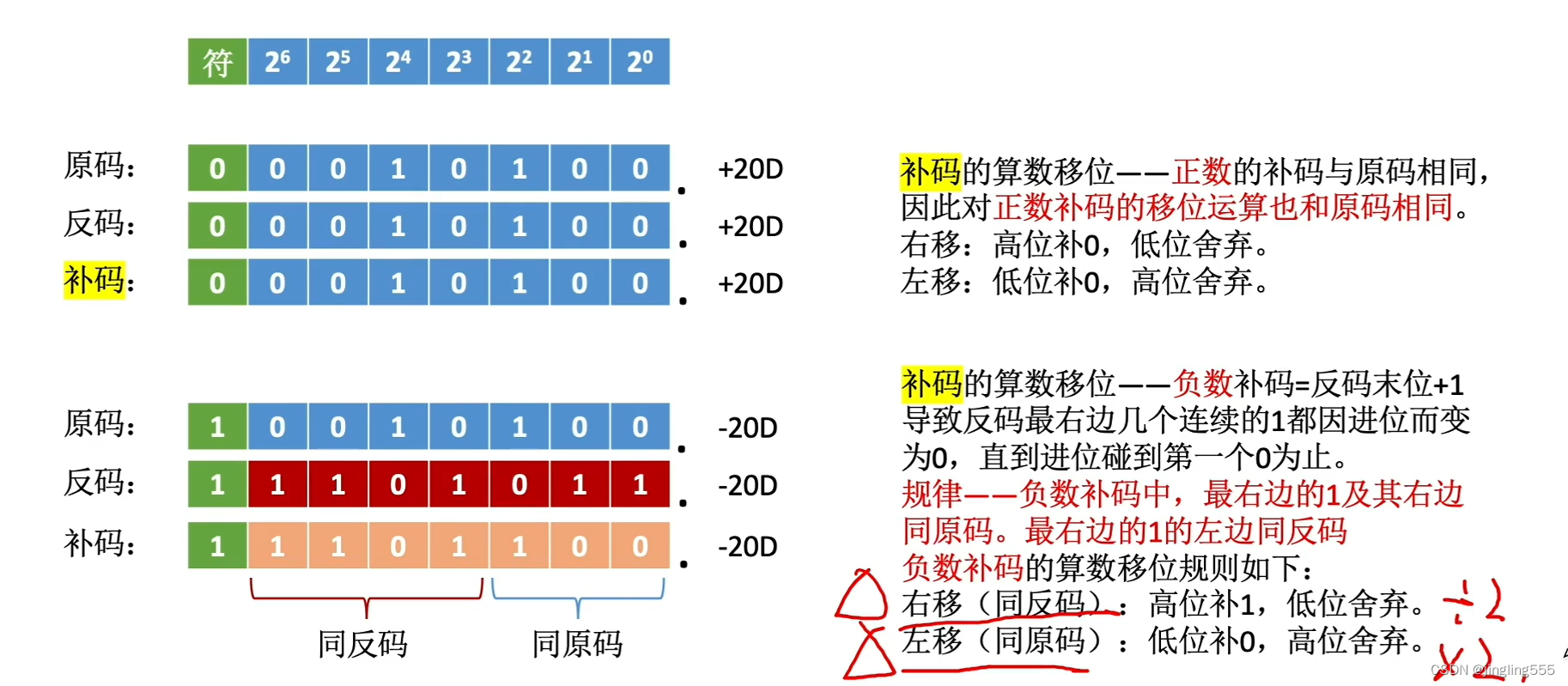
算数移位: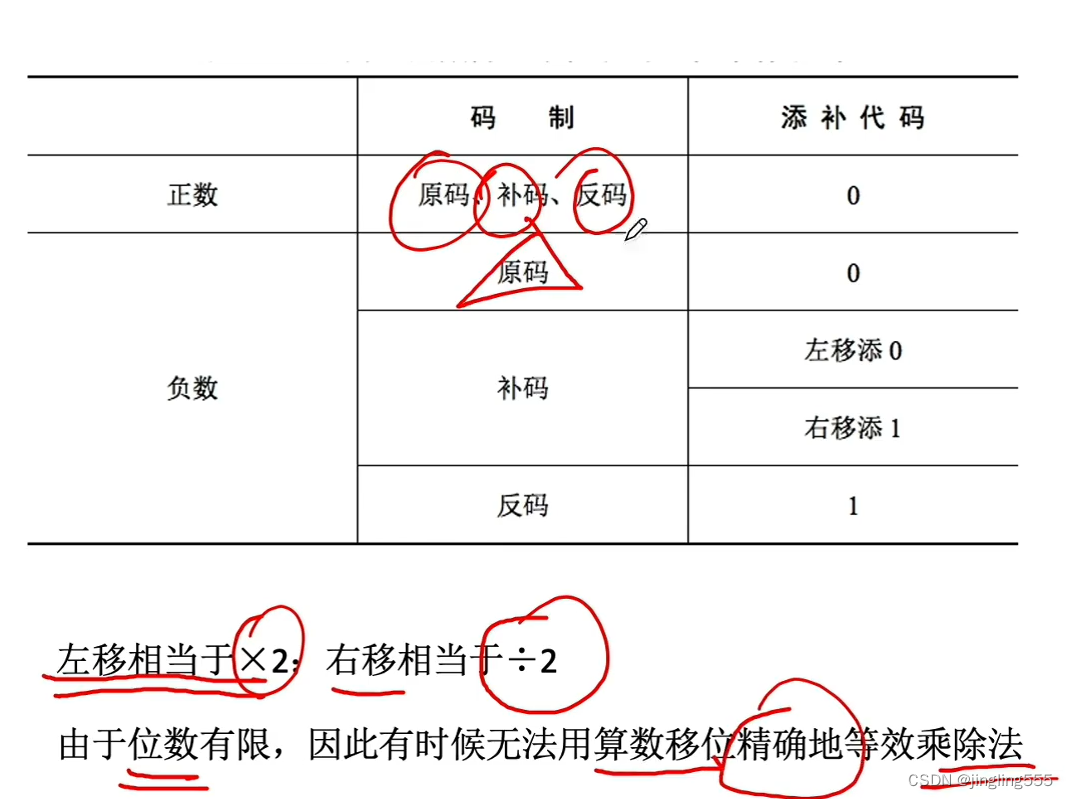
算数移位的应用举例:
逻辑移位: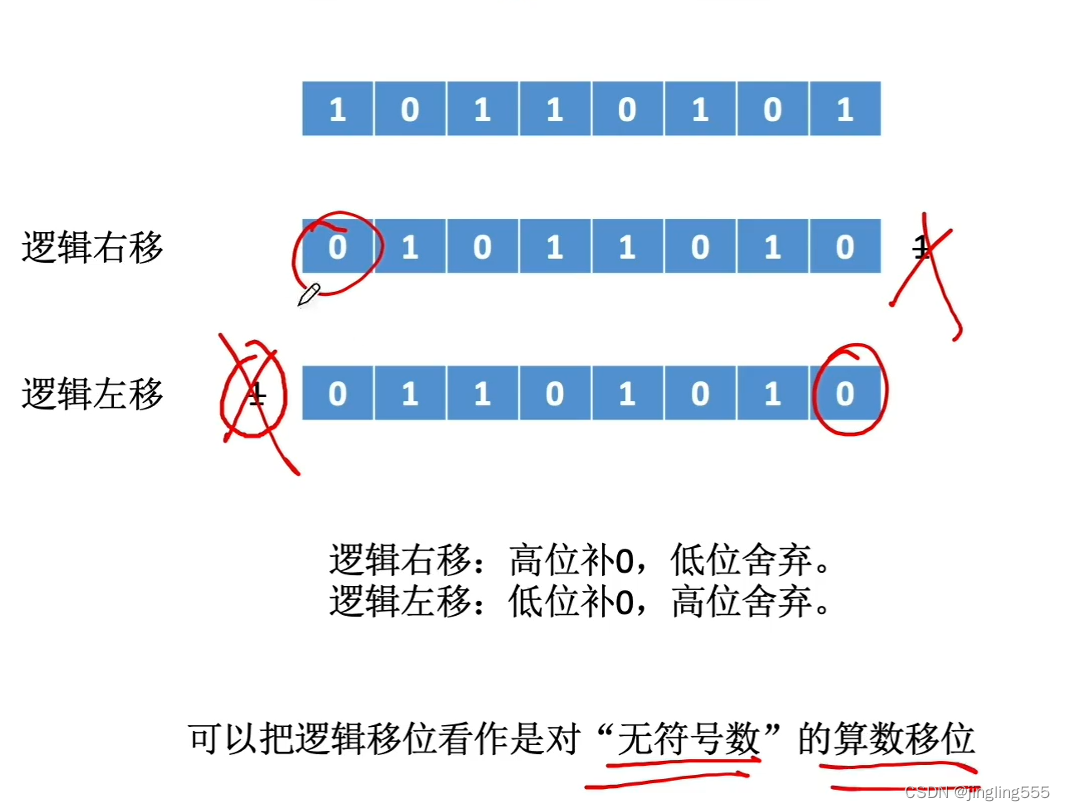
逻辑移位的应用举例: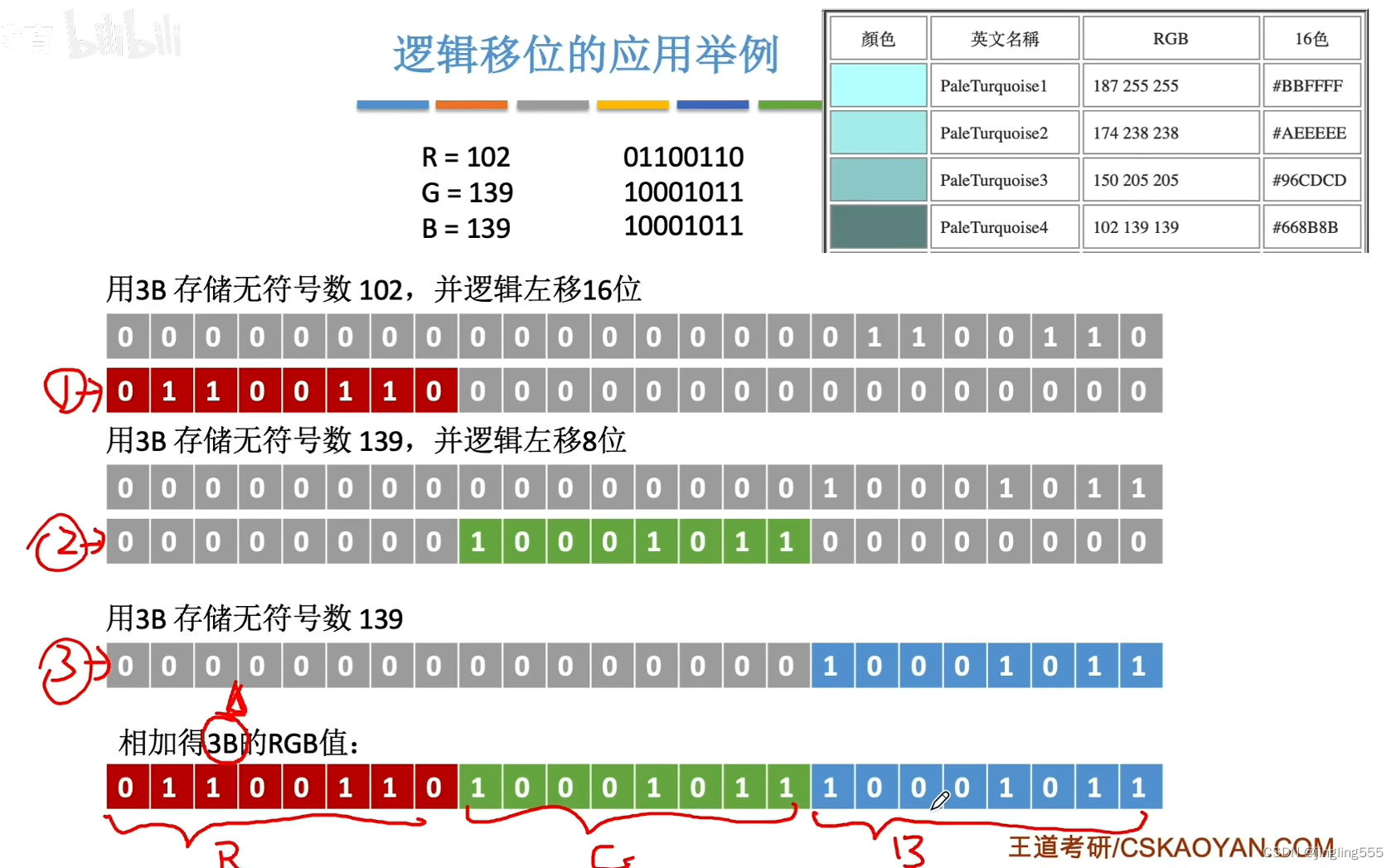
循环移位: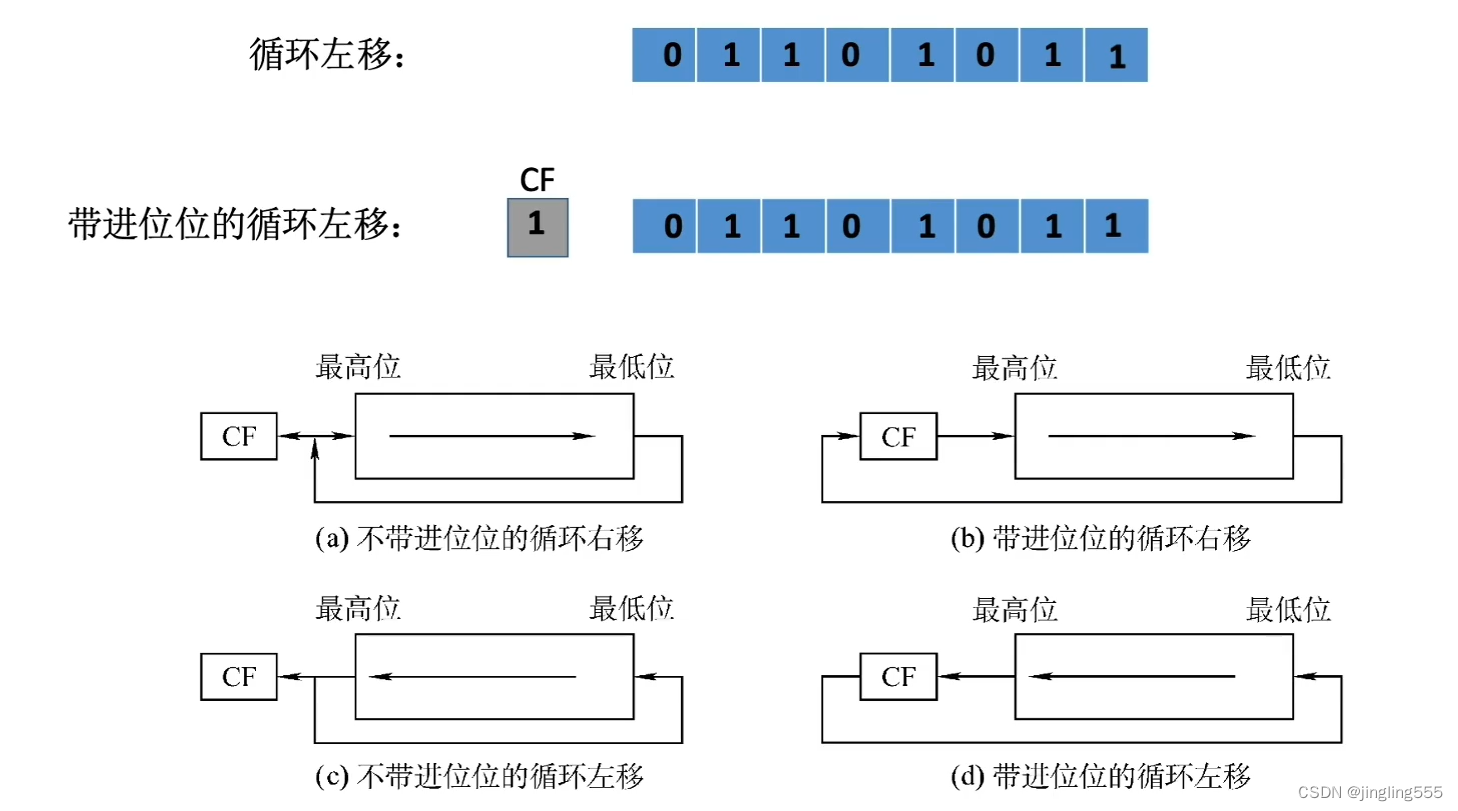
总结: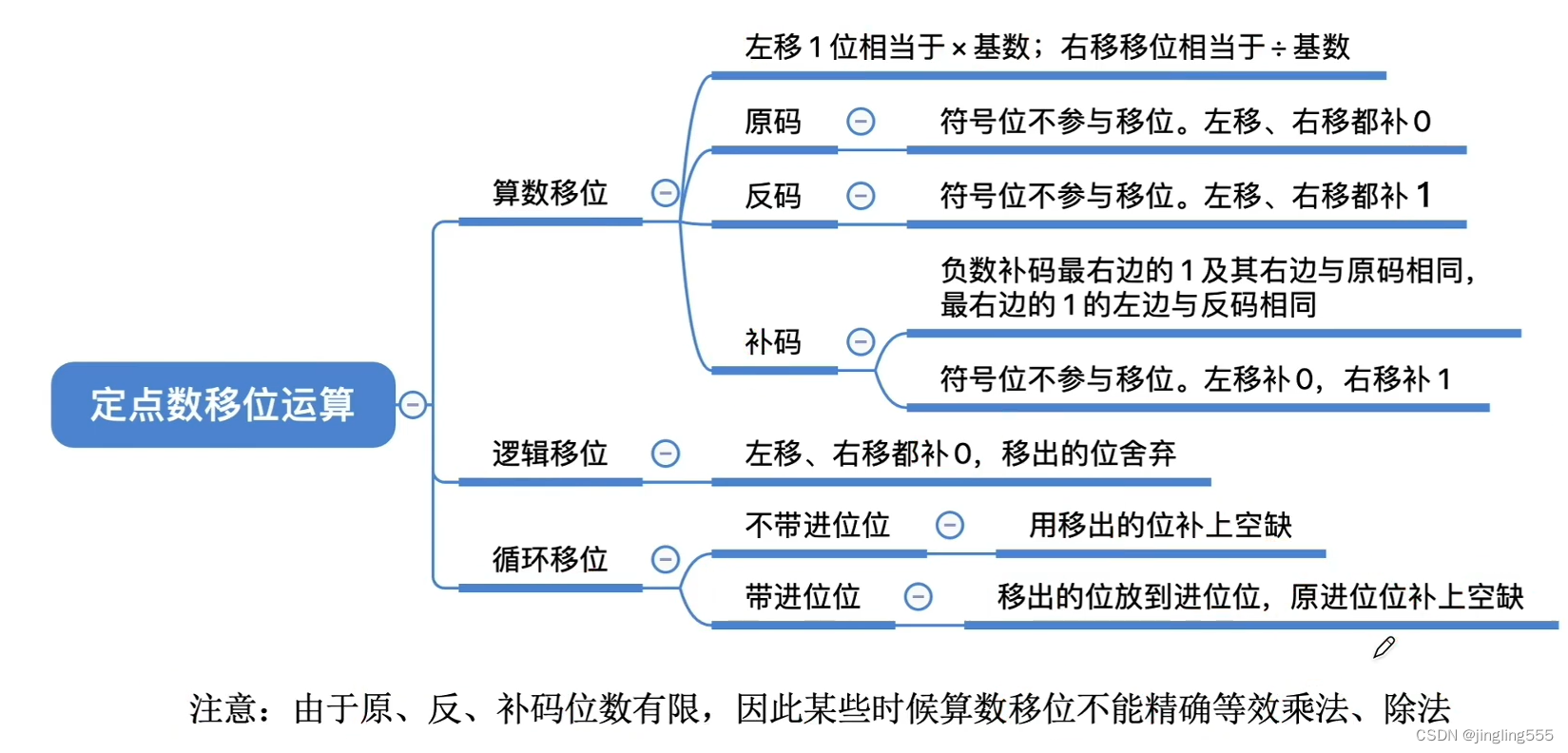
原码的乘法运算
手算乘法(二进制):
原码一位乘法:
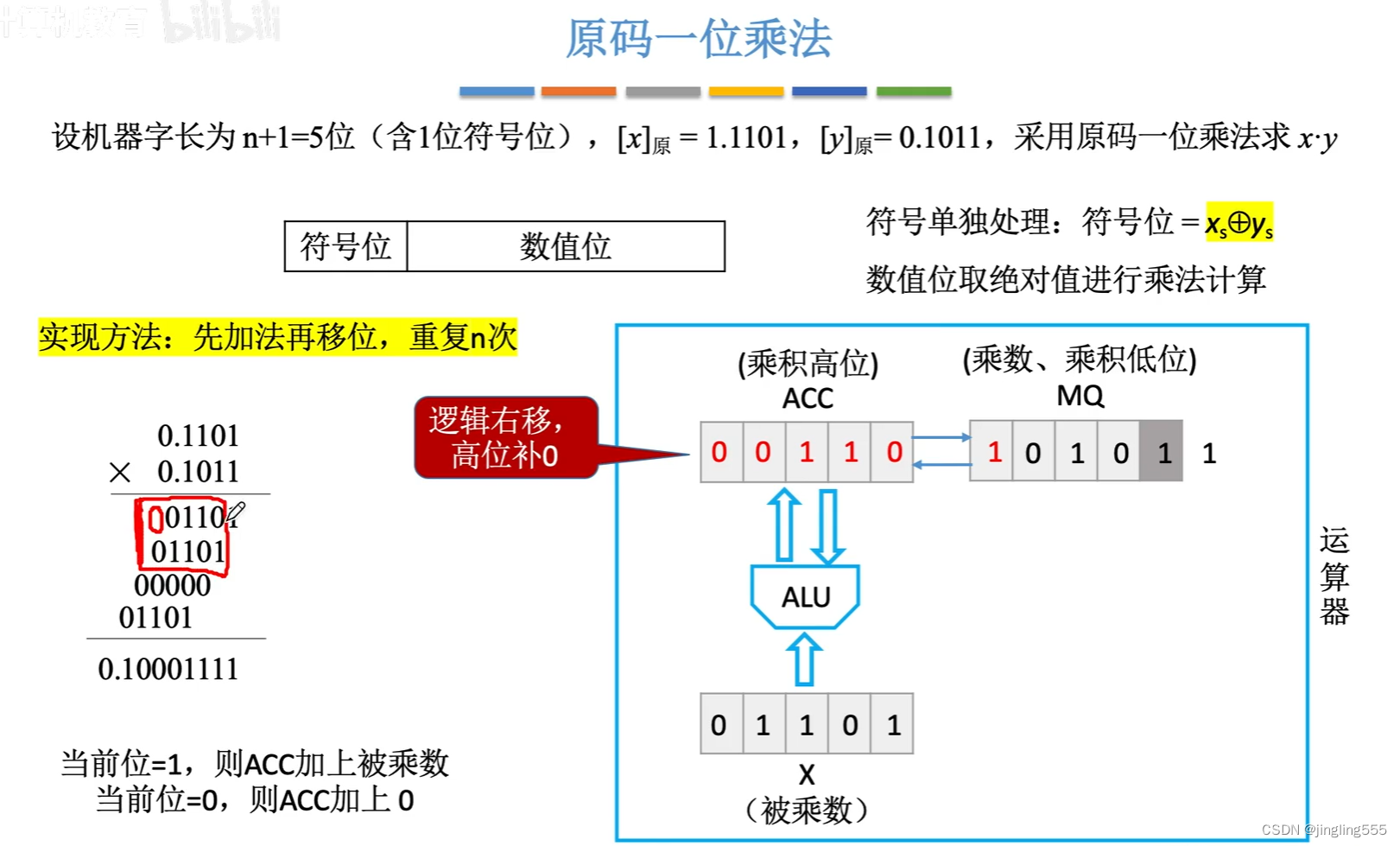
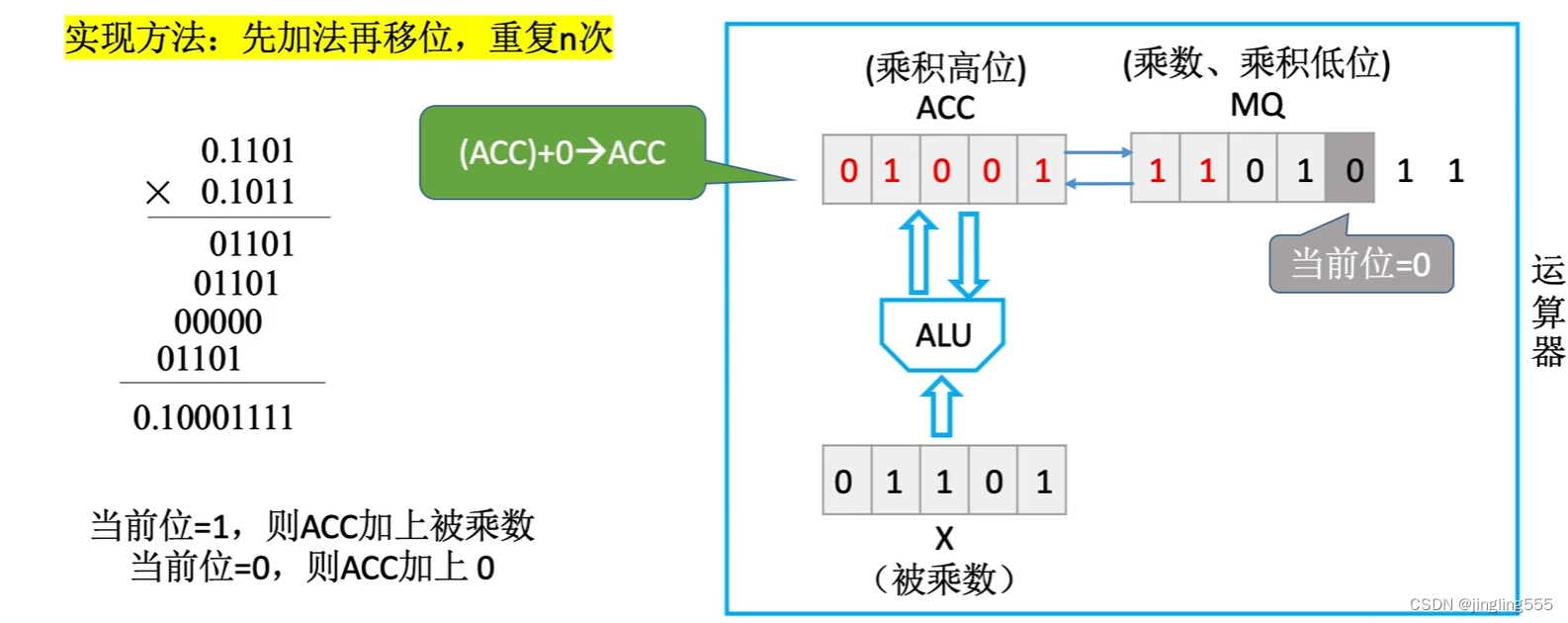
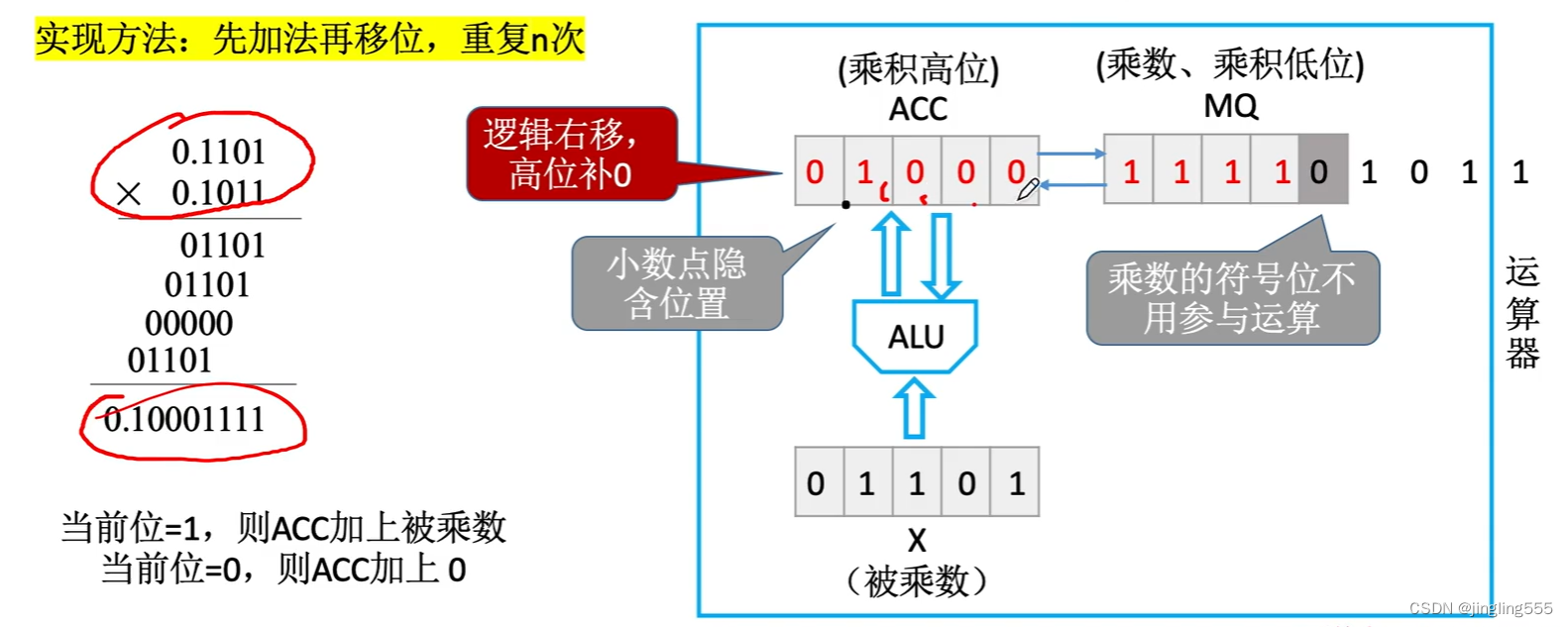
运算器的基本组成: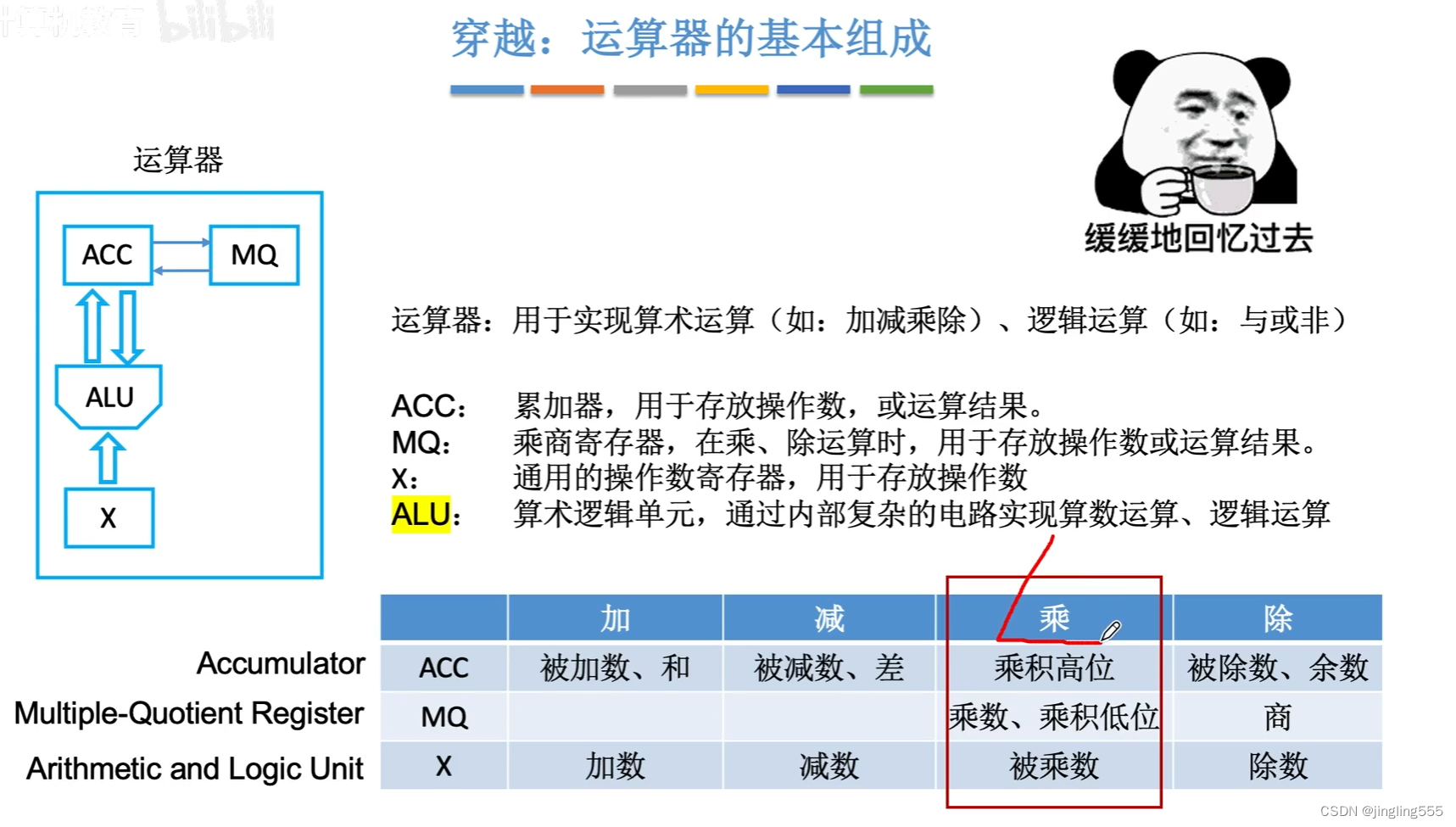
原码一位乘法(手算模拟):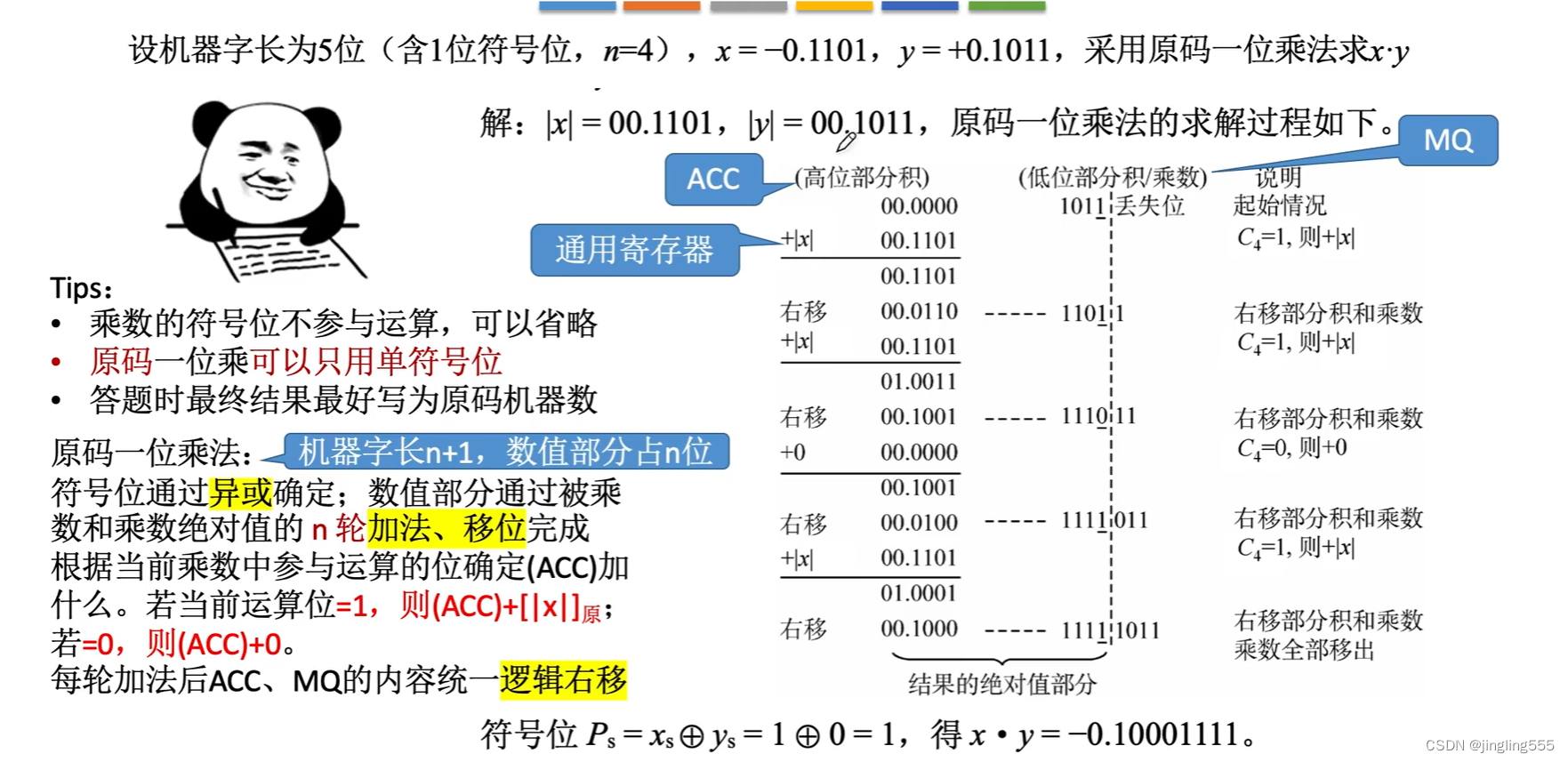
补码的乘法运算
补码一位乘法: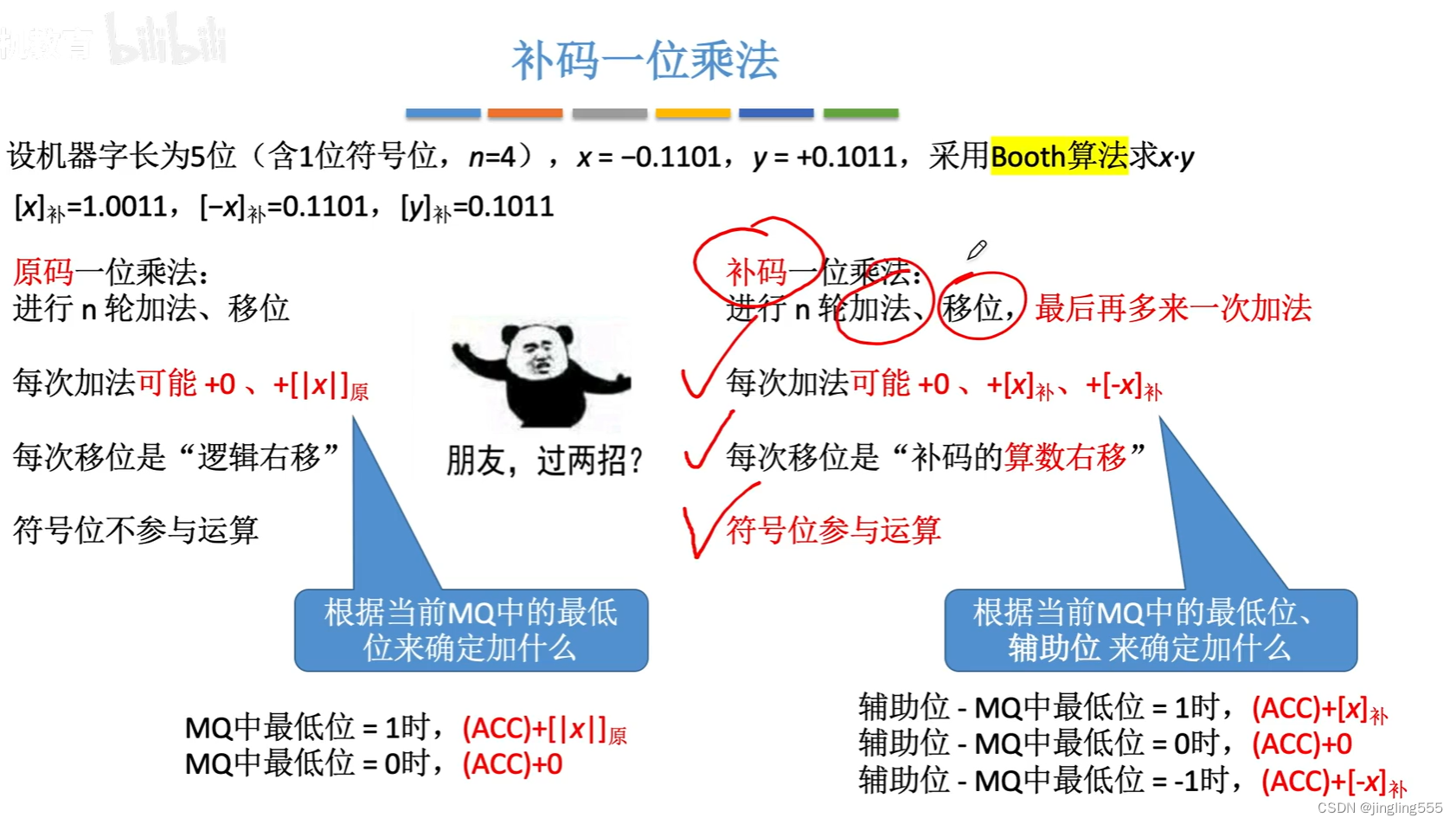
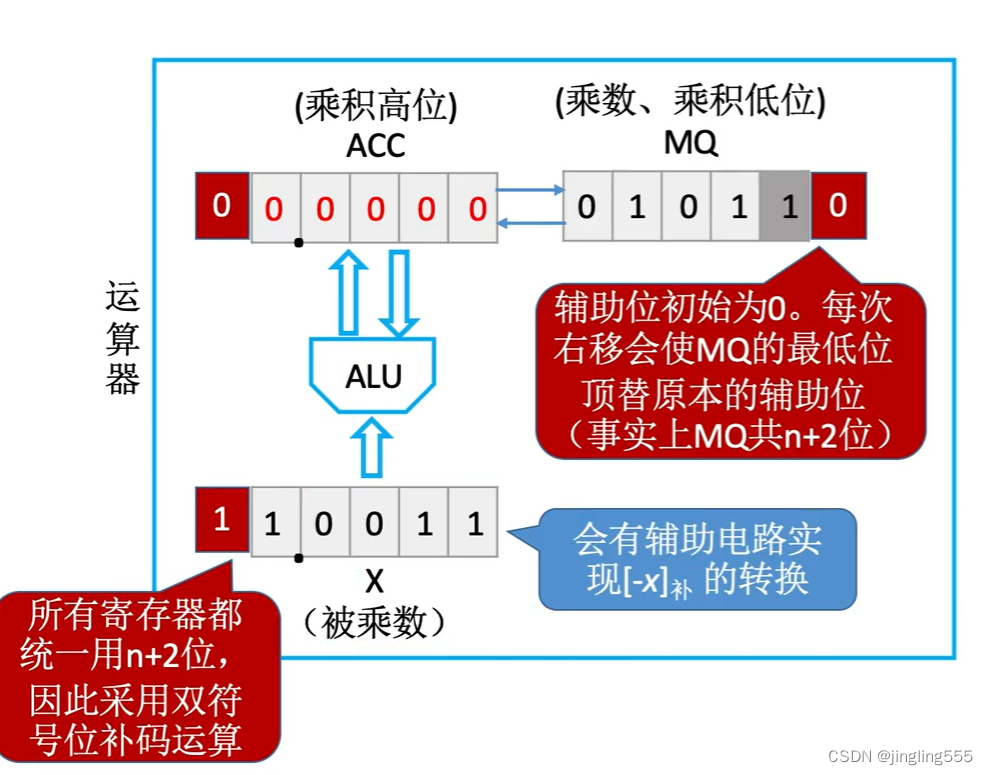
补码一位乘法(手算模拟):
总结:
原码的除法运算
手算除法(二进制):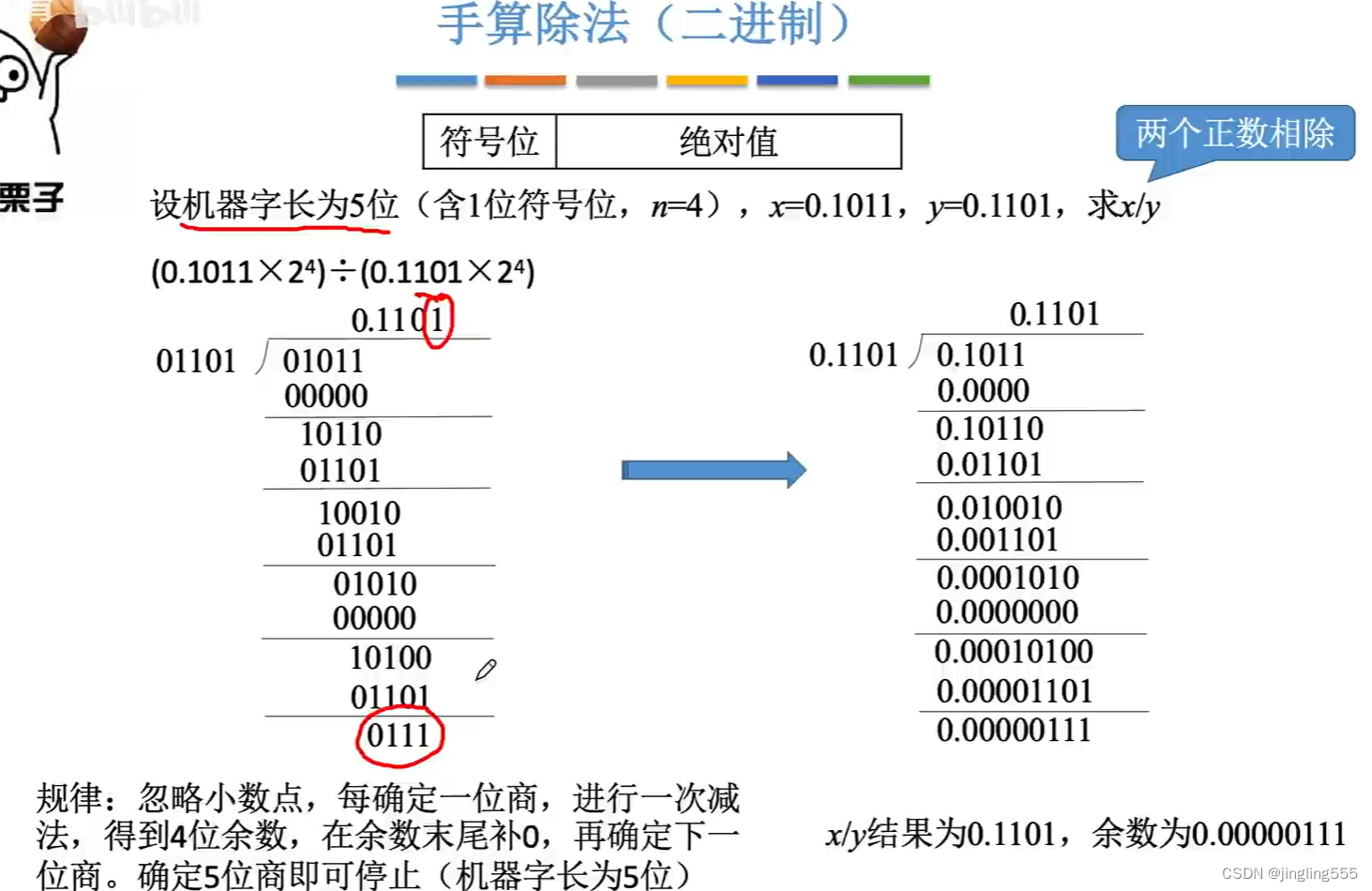
原码除法:恢复余数法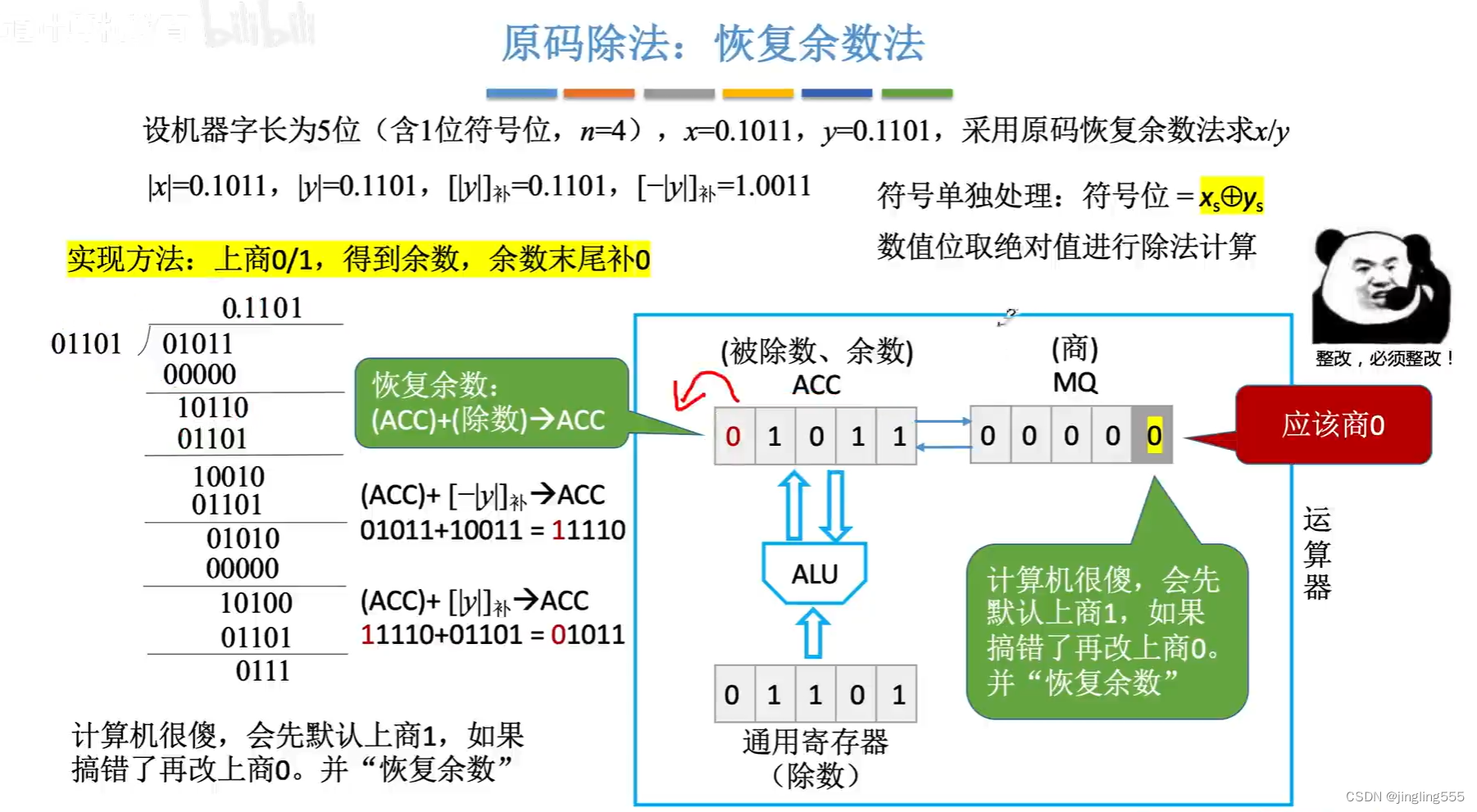
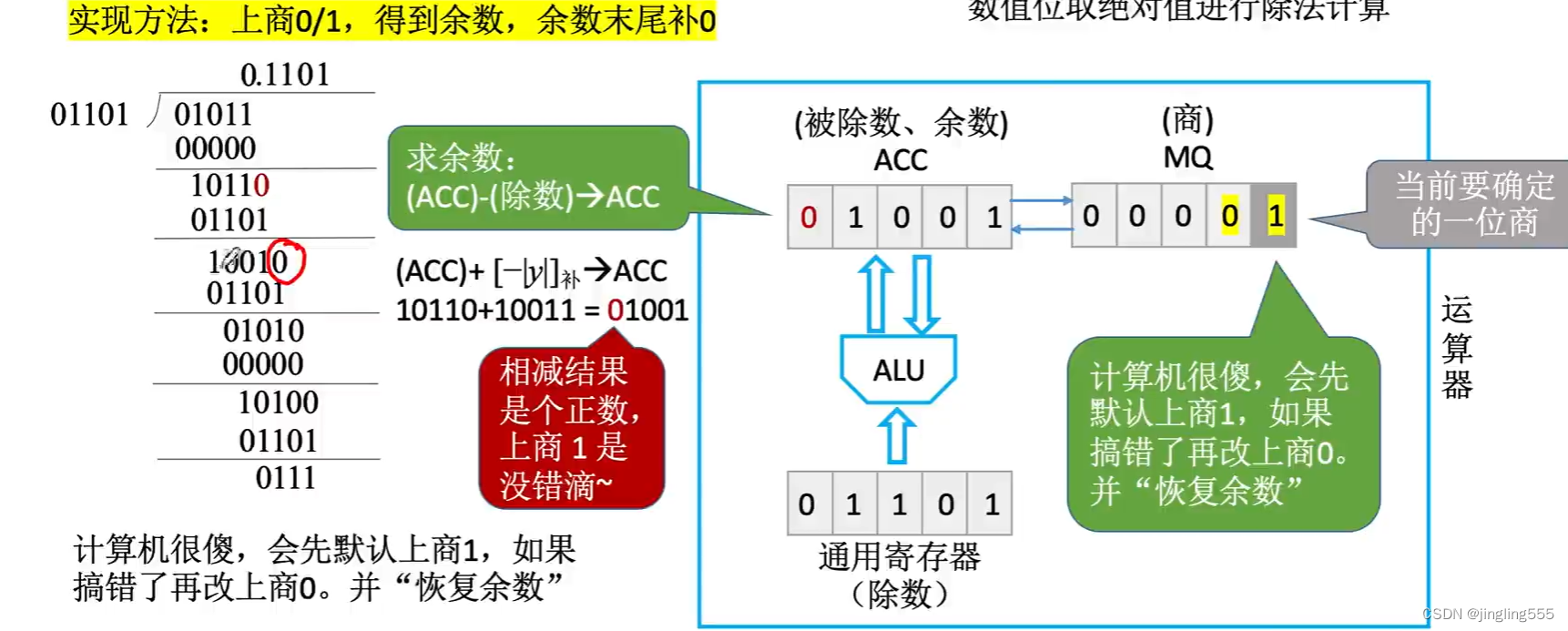
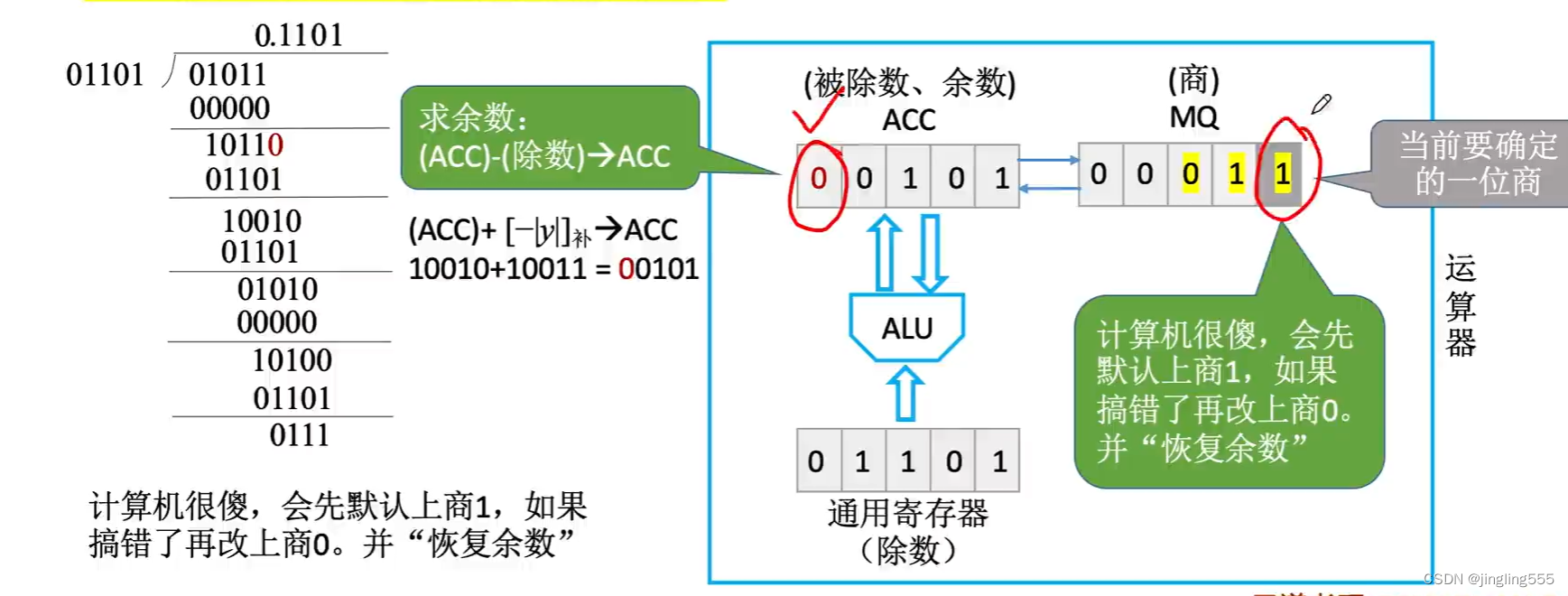
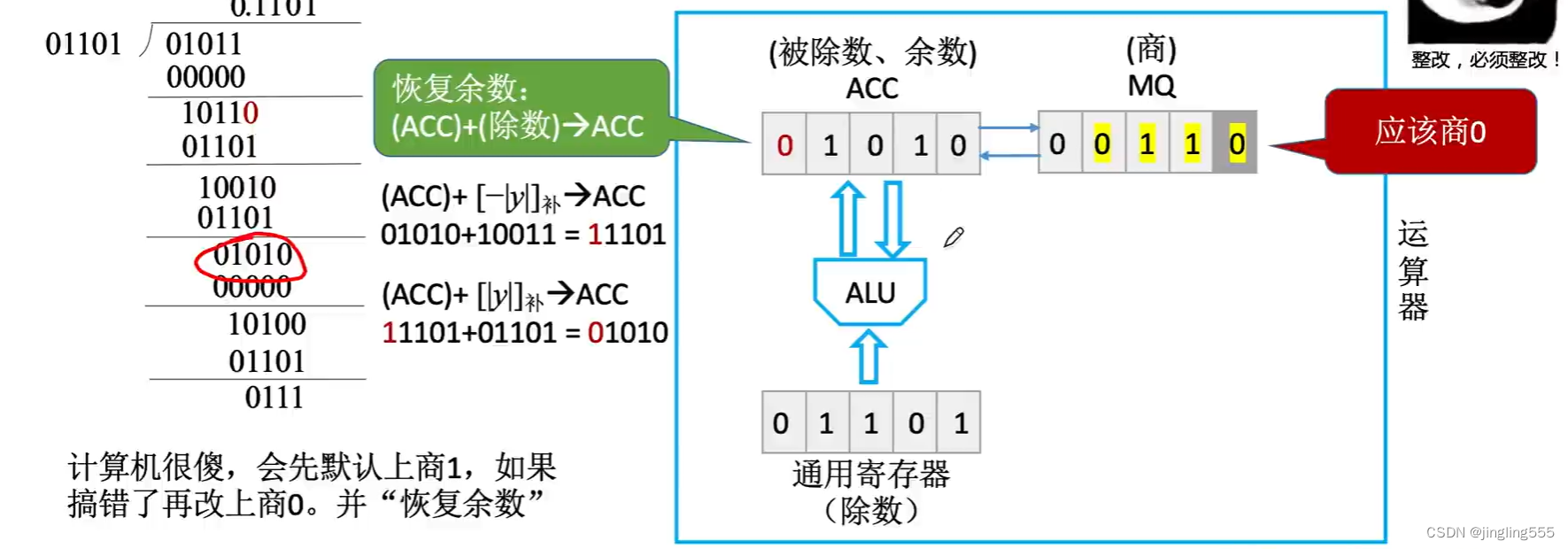
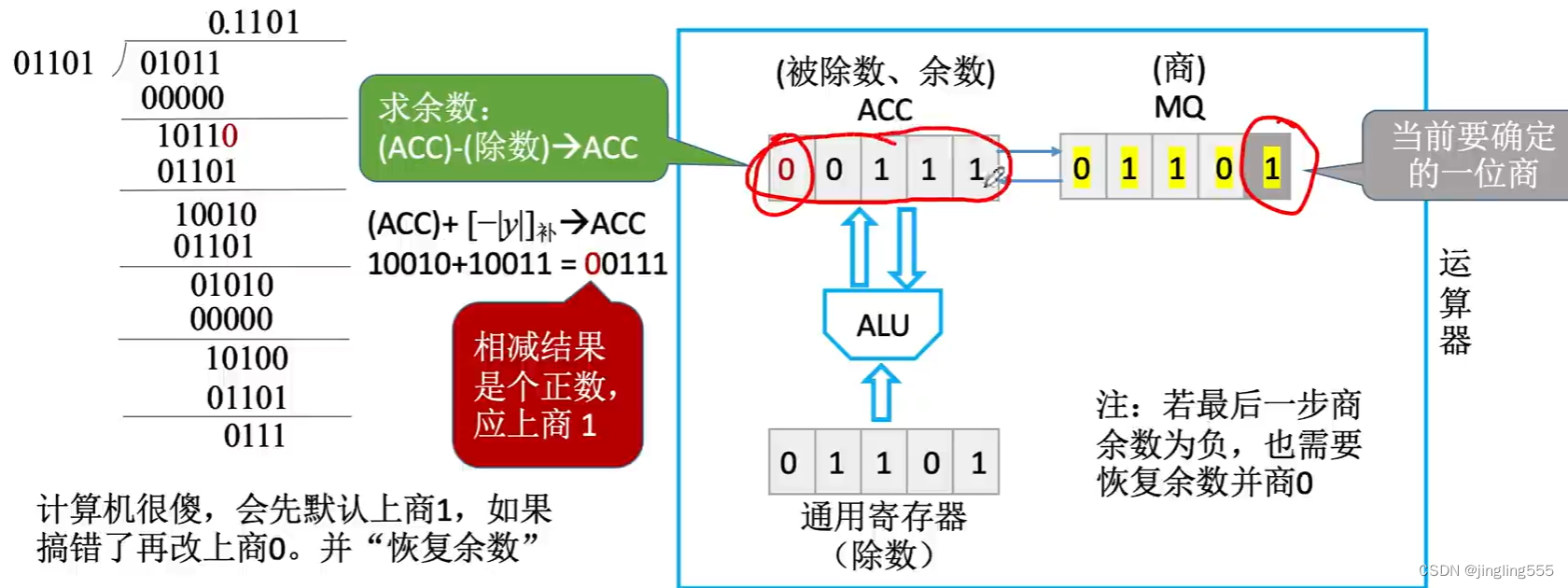
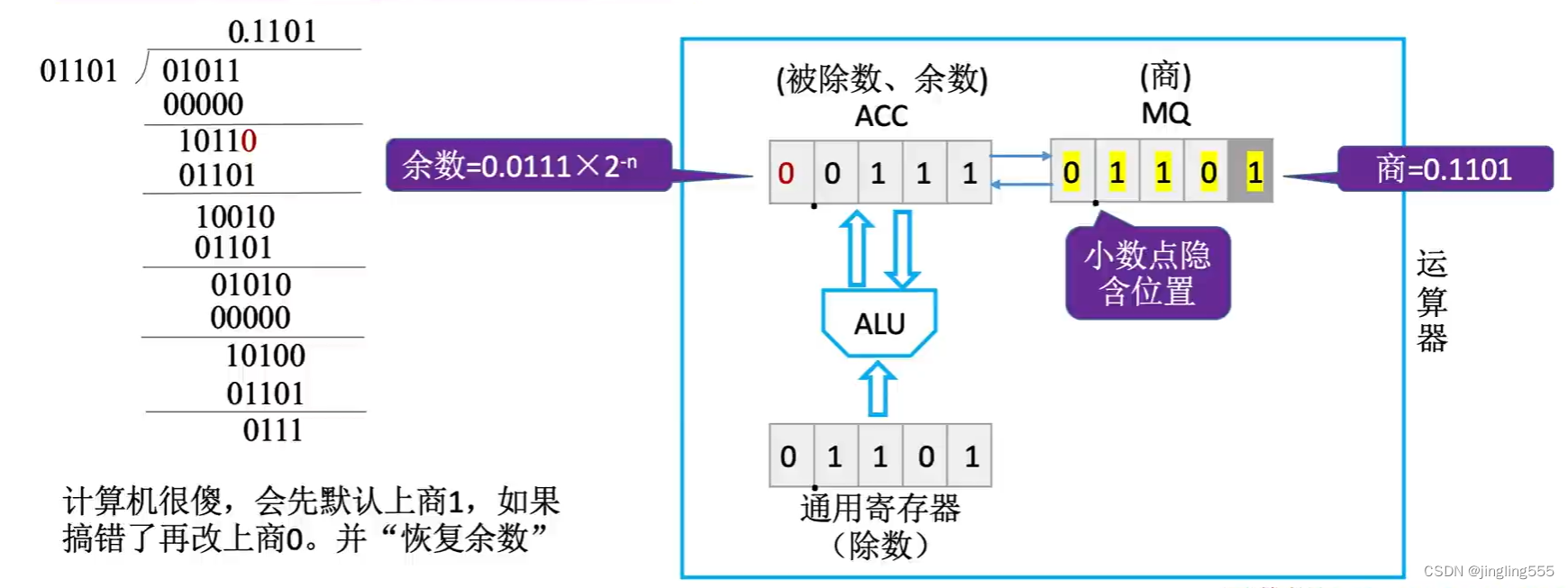
原码除法:恢复余数法(手算)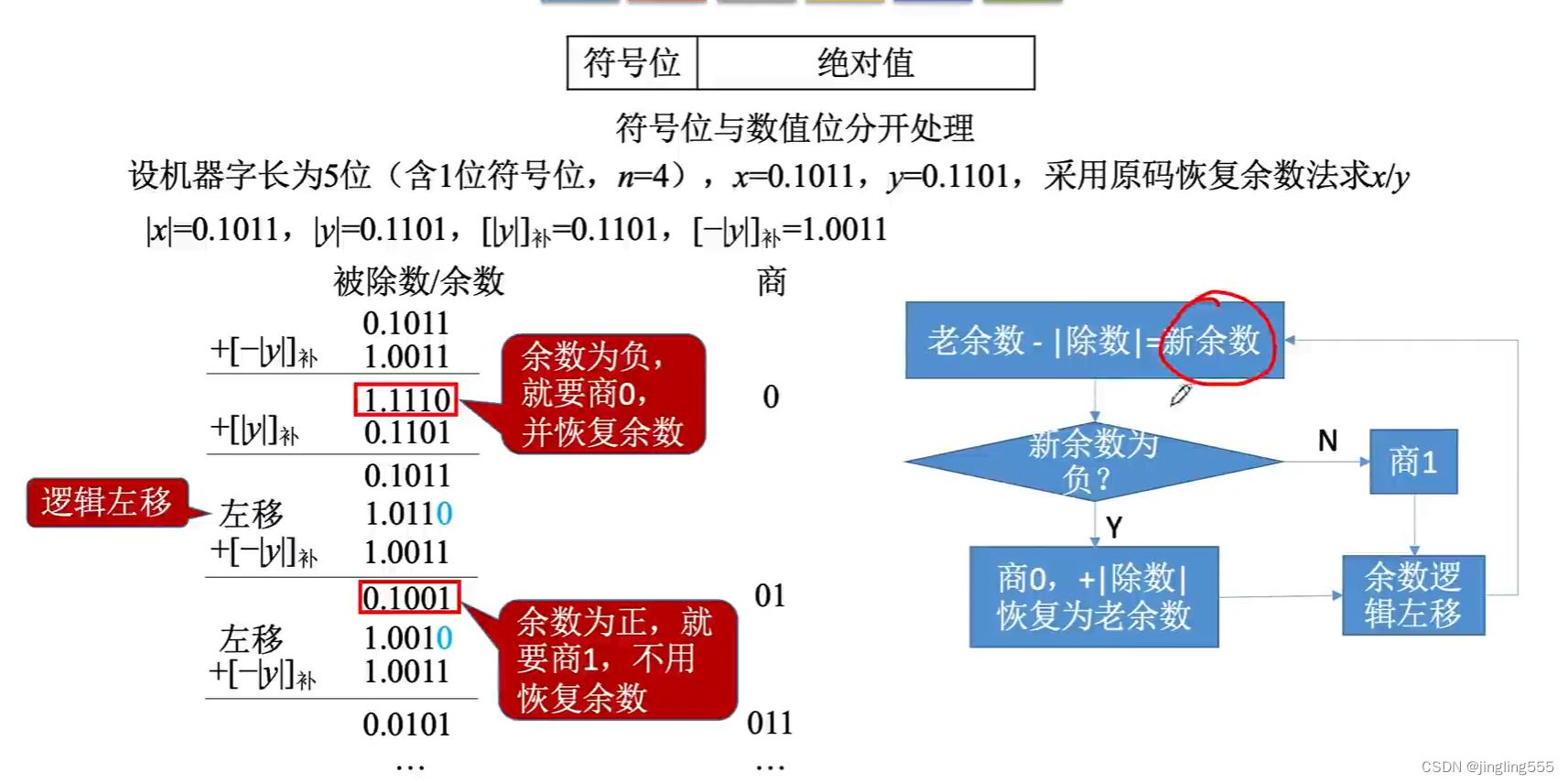
原码除法:加减交替法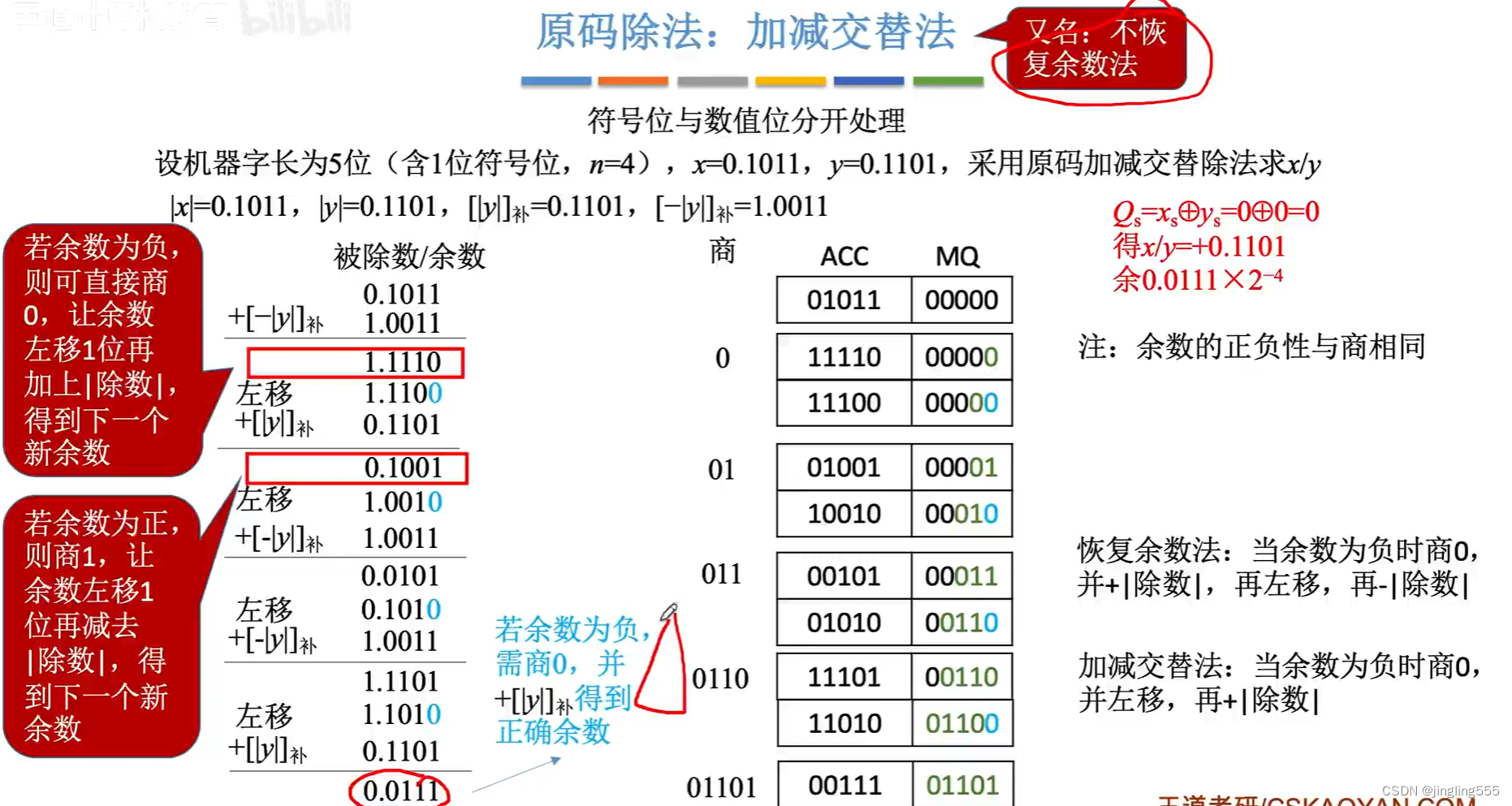
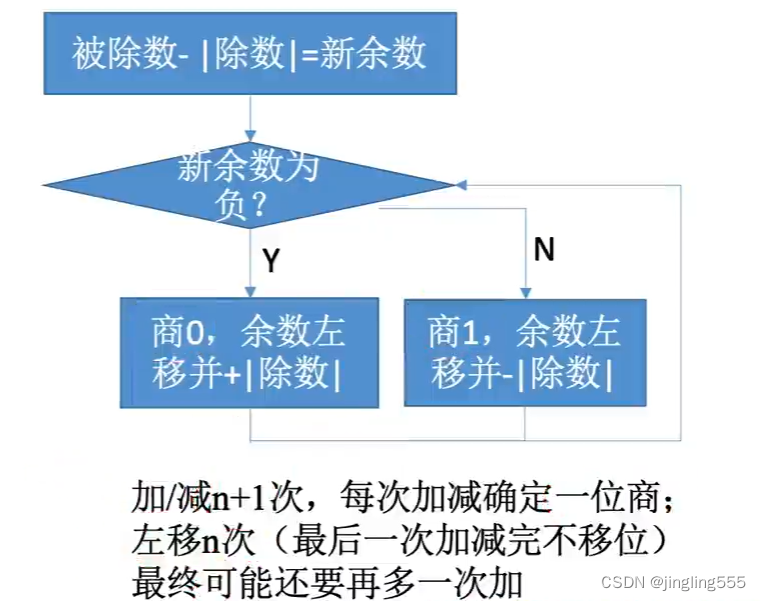
补码的除法运算
补码除法:加减交替法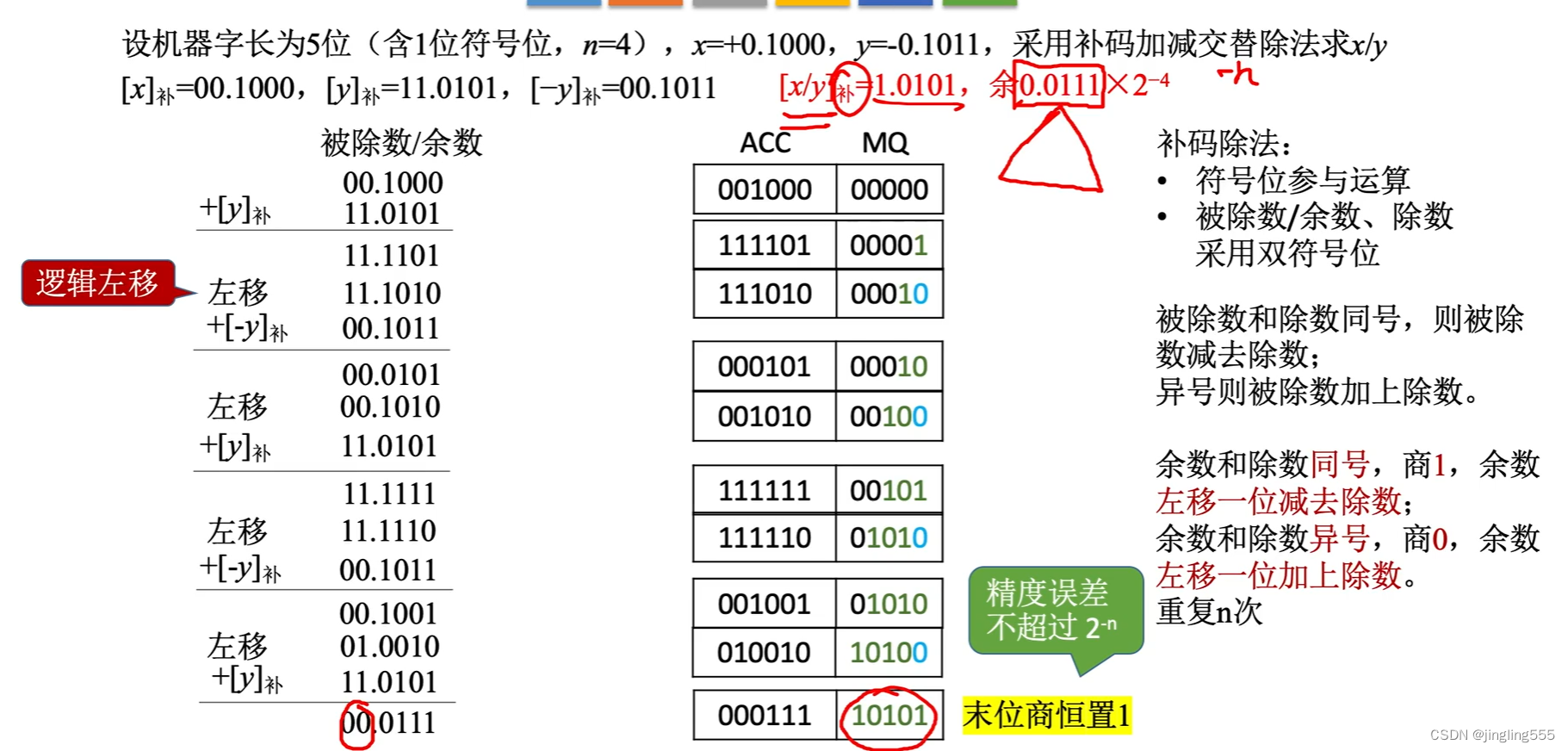
总结: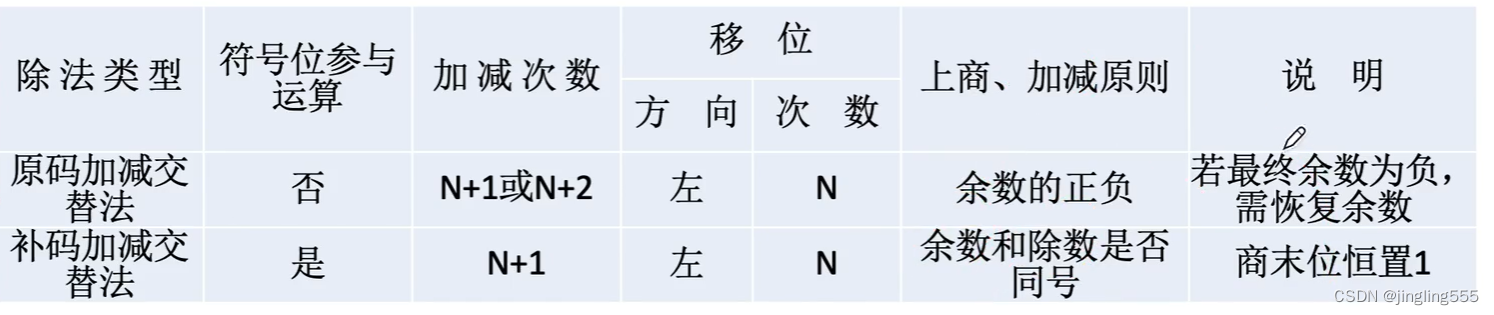
C语言中的强制类型转换
强制类型转换: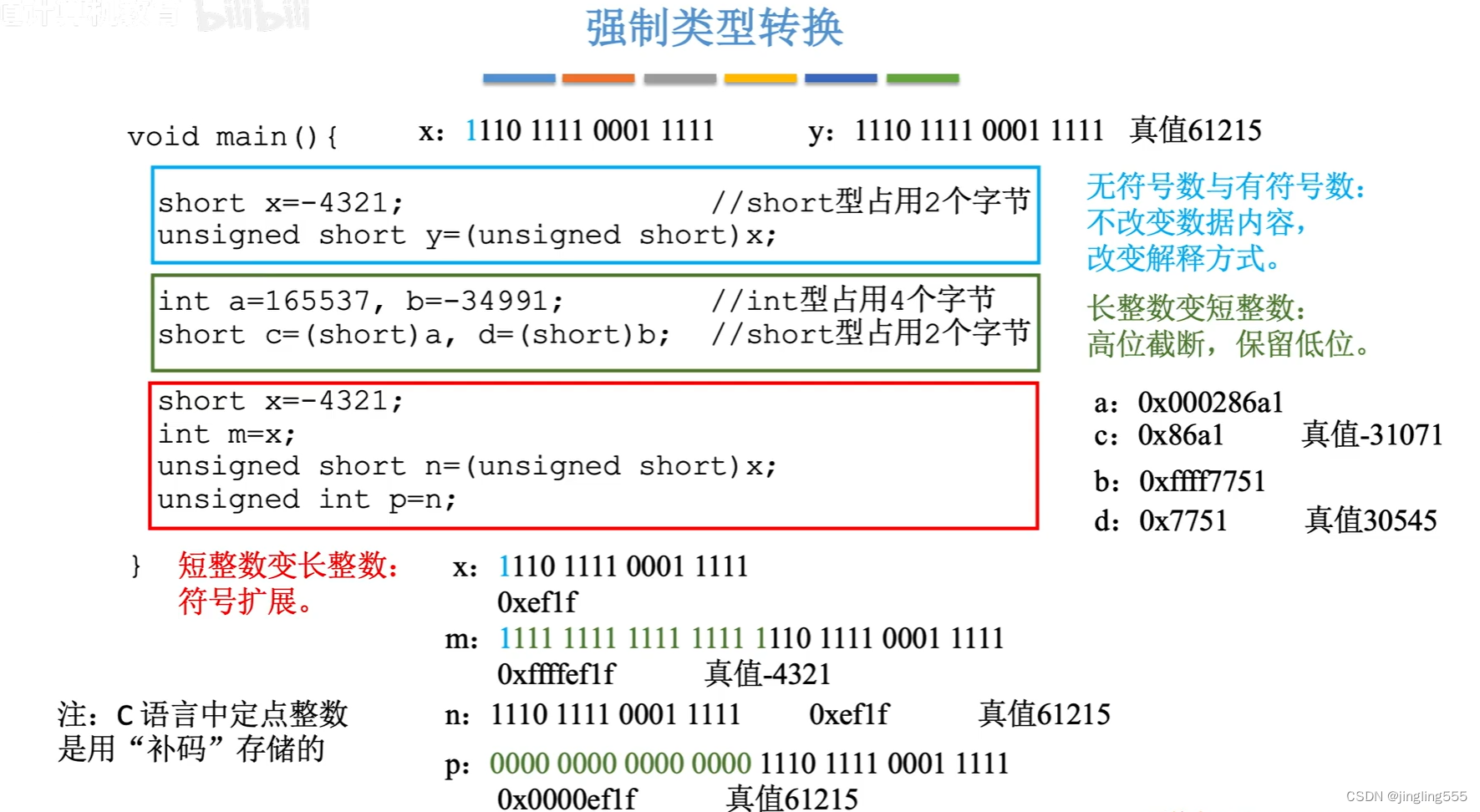
数据的存储和排列
大小端模式: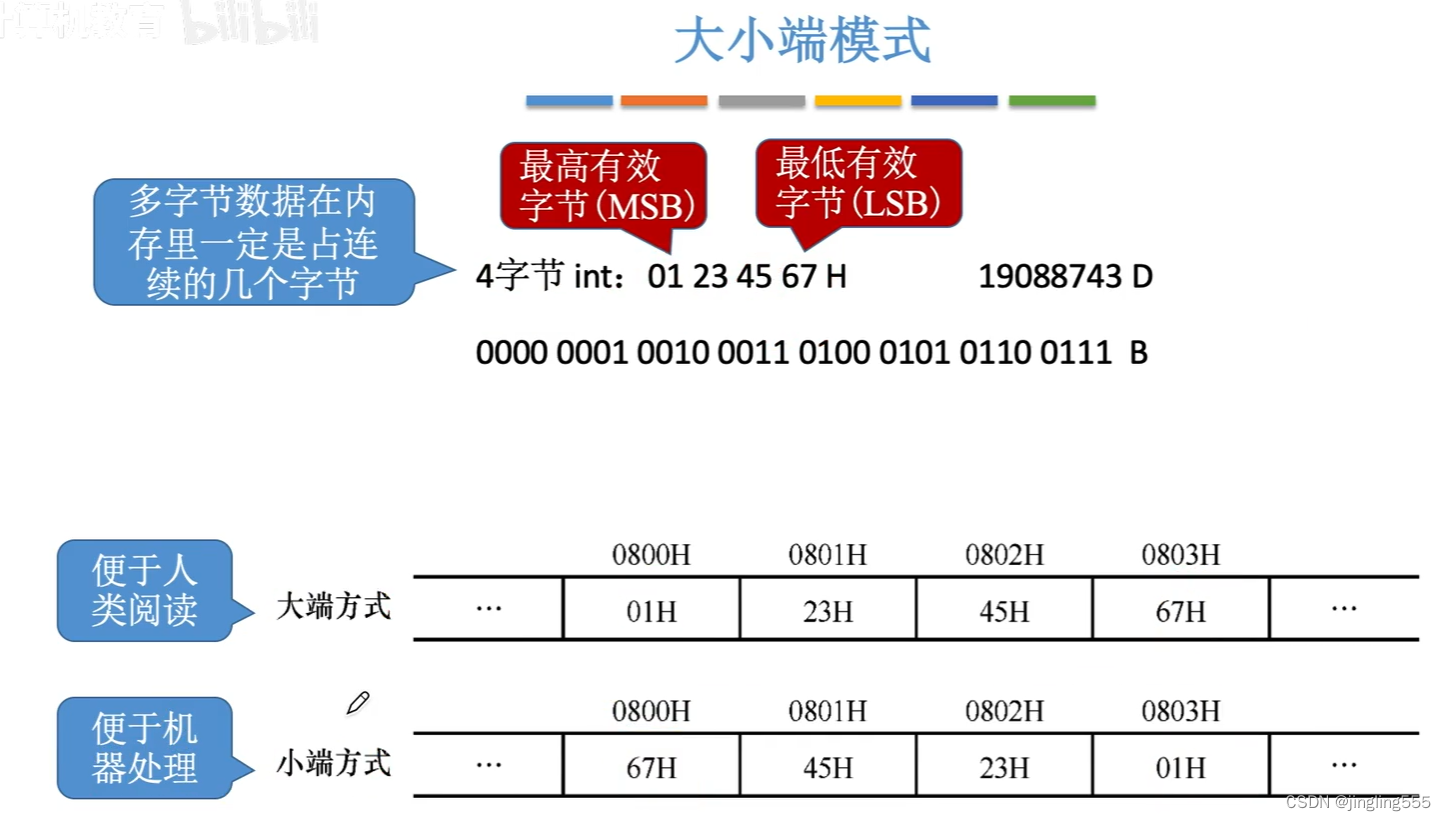
边界对齐: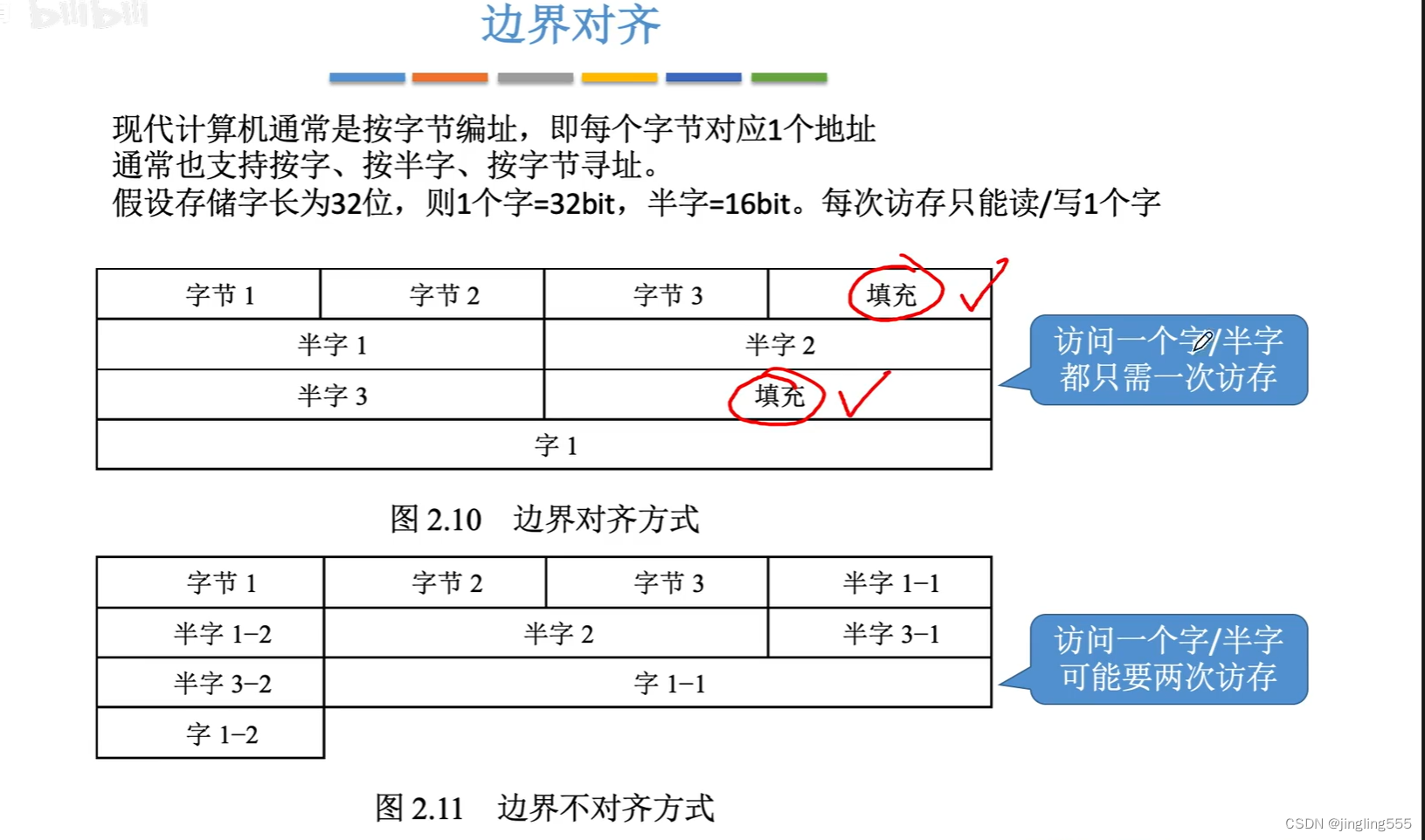
浮点数的表示
从科学计数法理解浮点数:
浮点数的表示: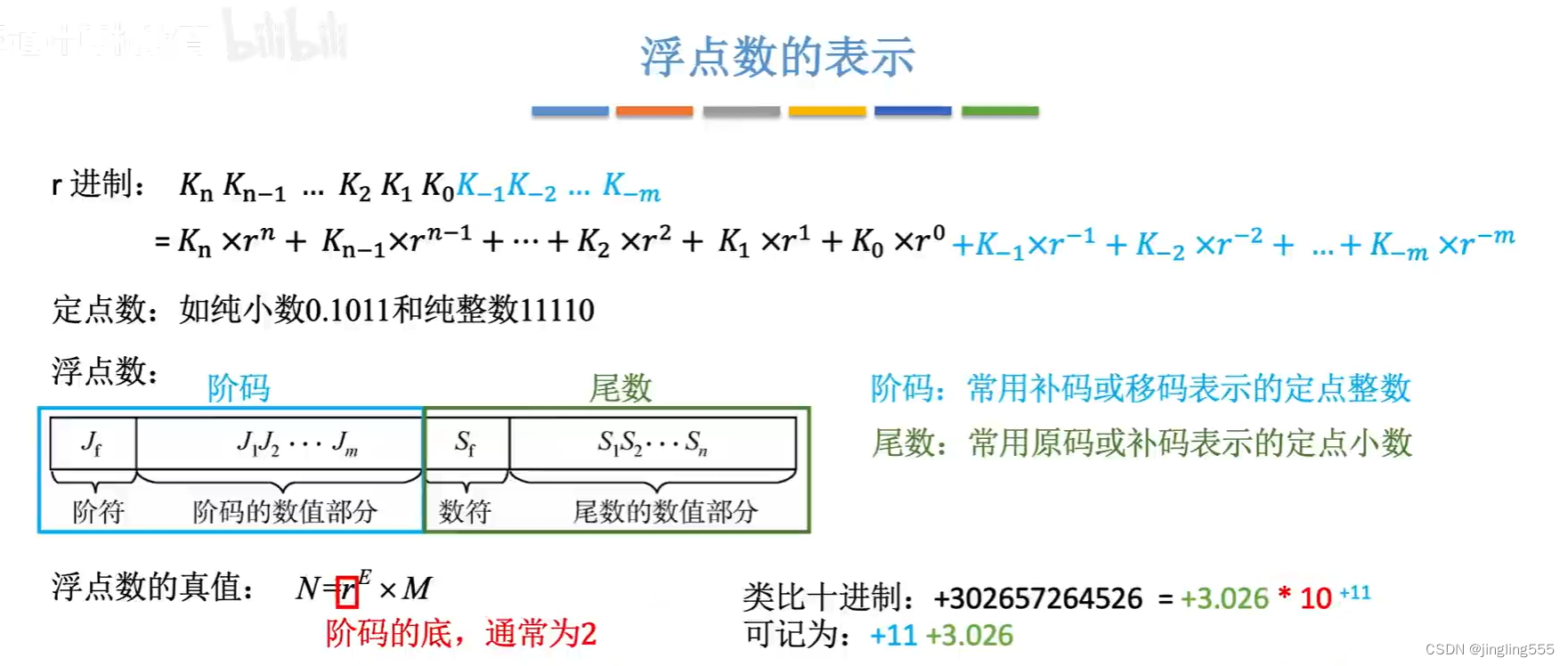



浮点数尾数的规格化: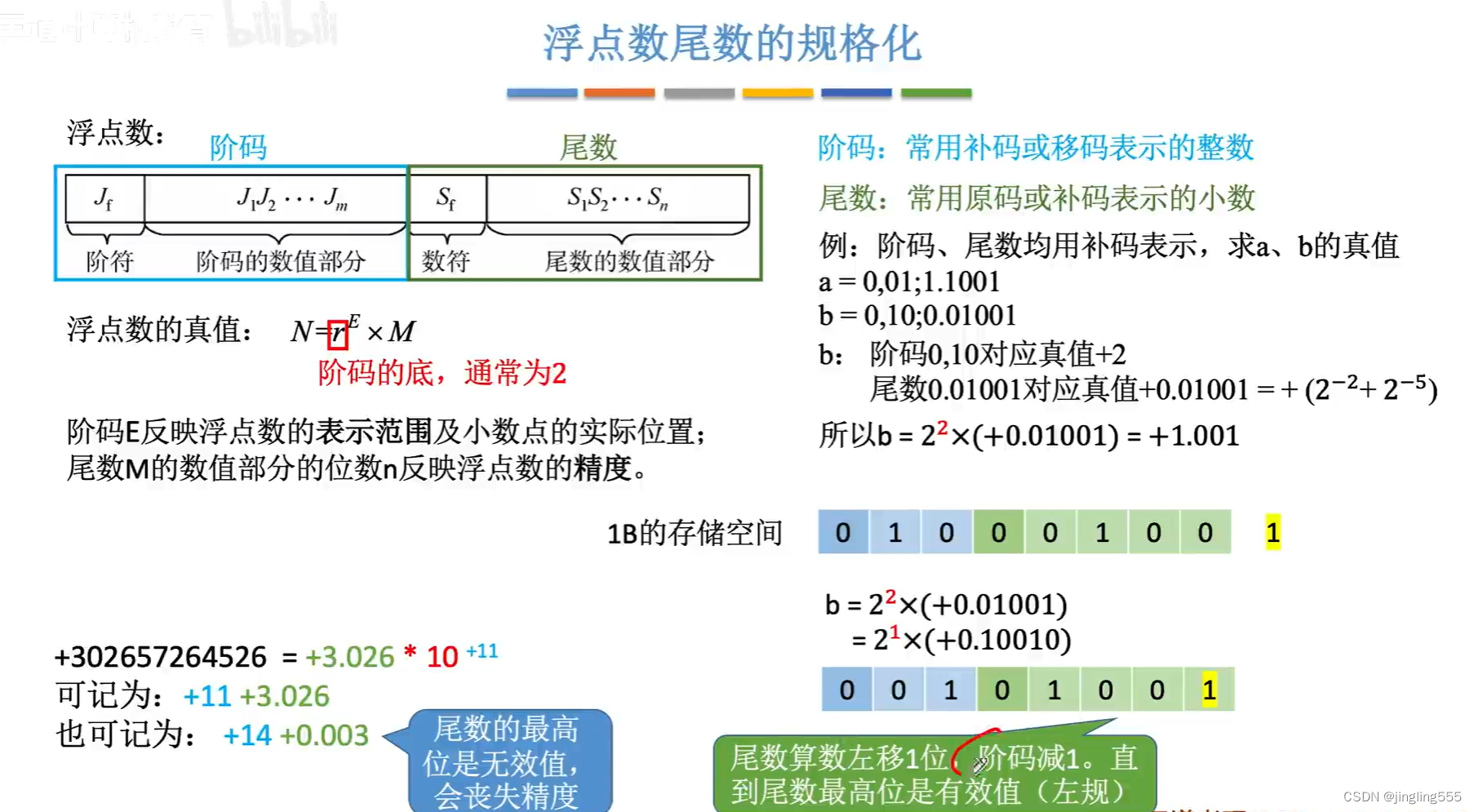

规格化浮点数的特点:

总结: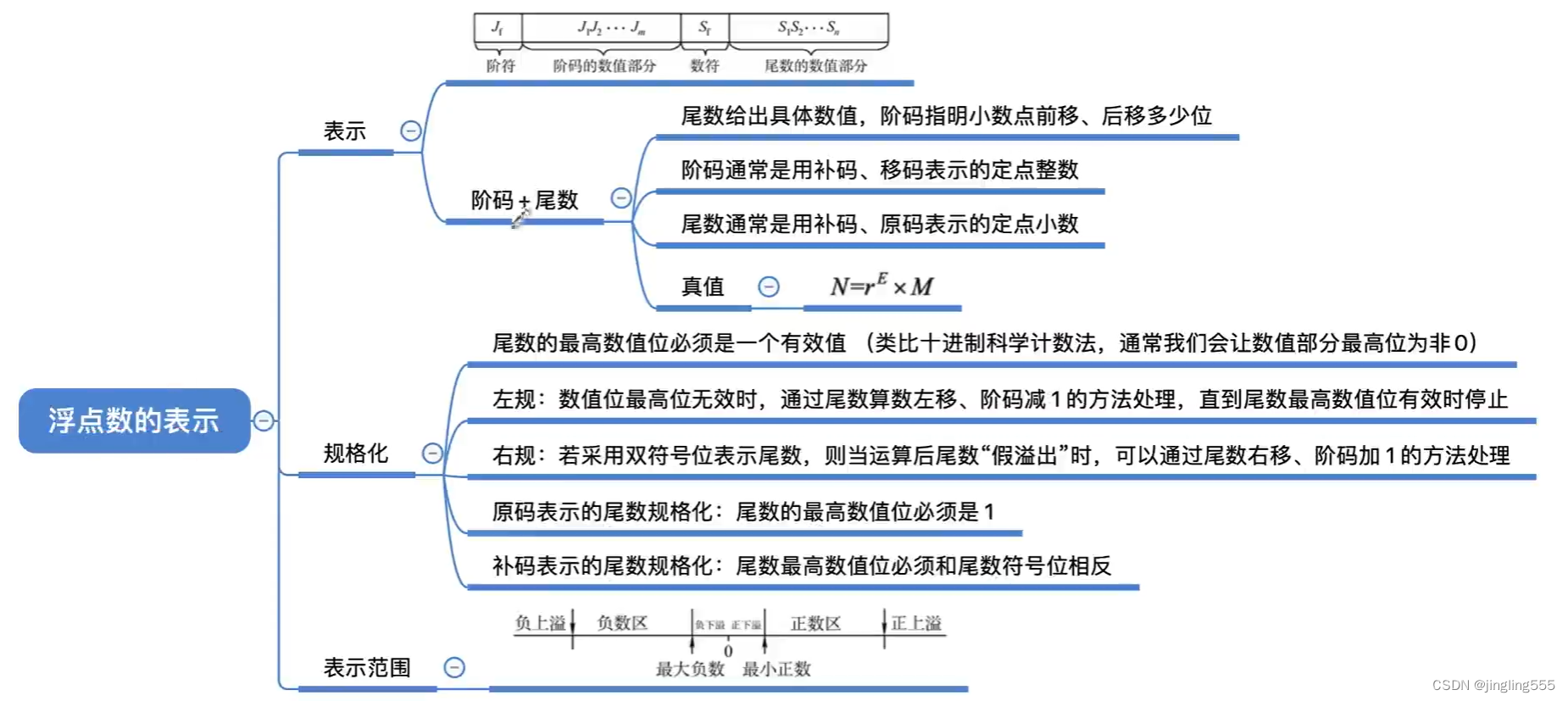
浮点数标准:IEEE 754
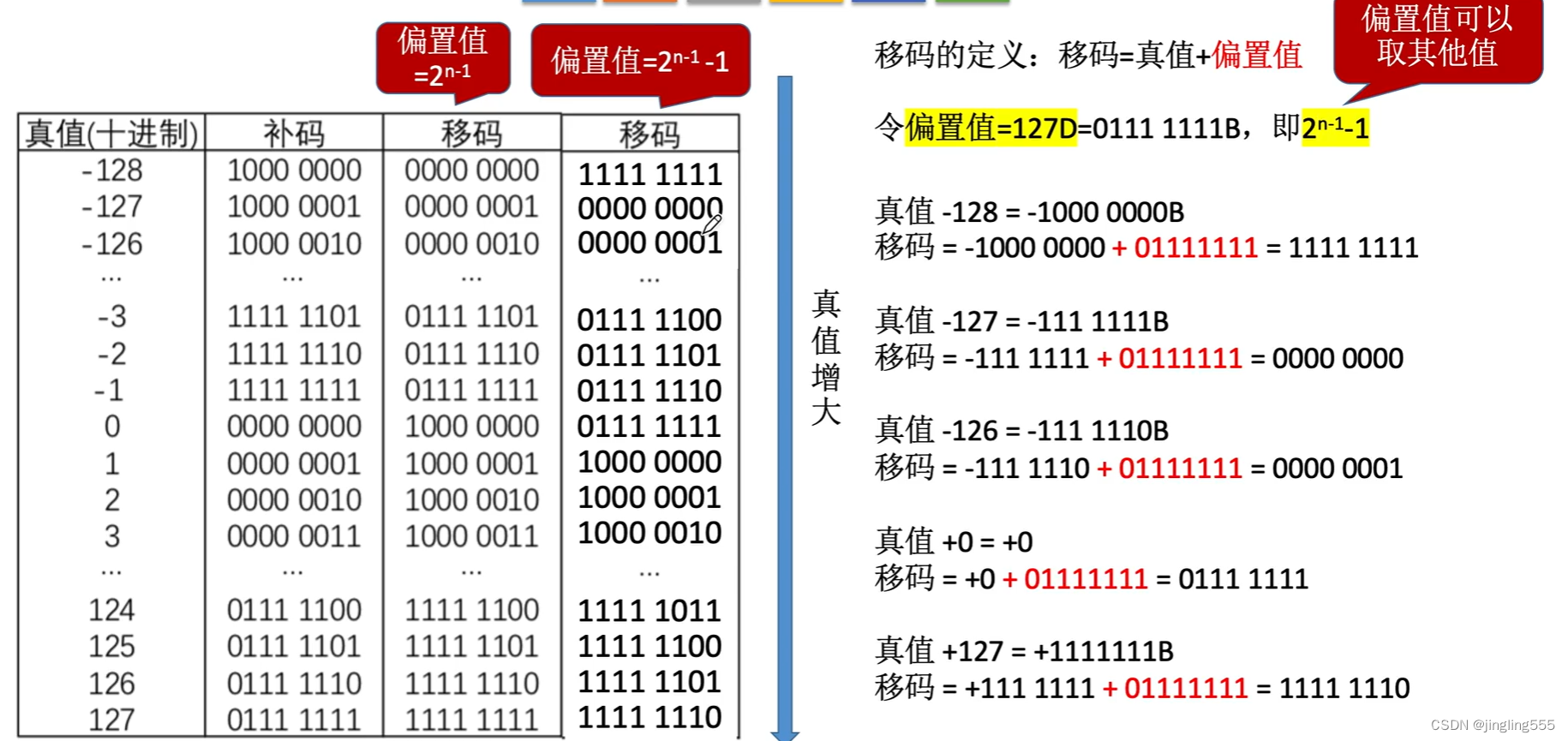
移码:
IEEE 754标准: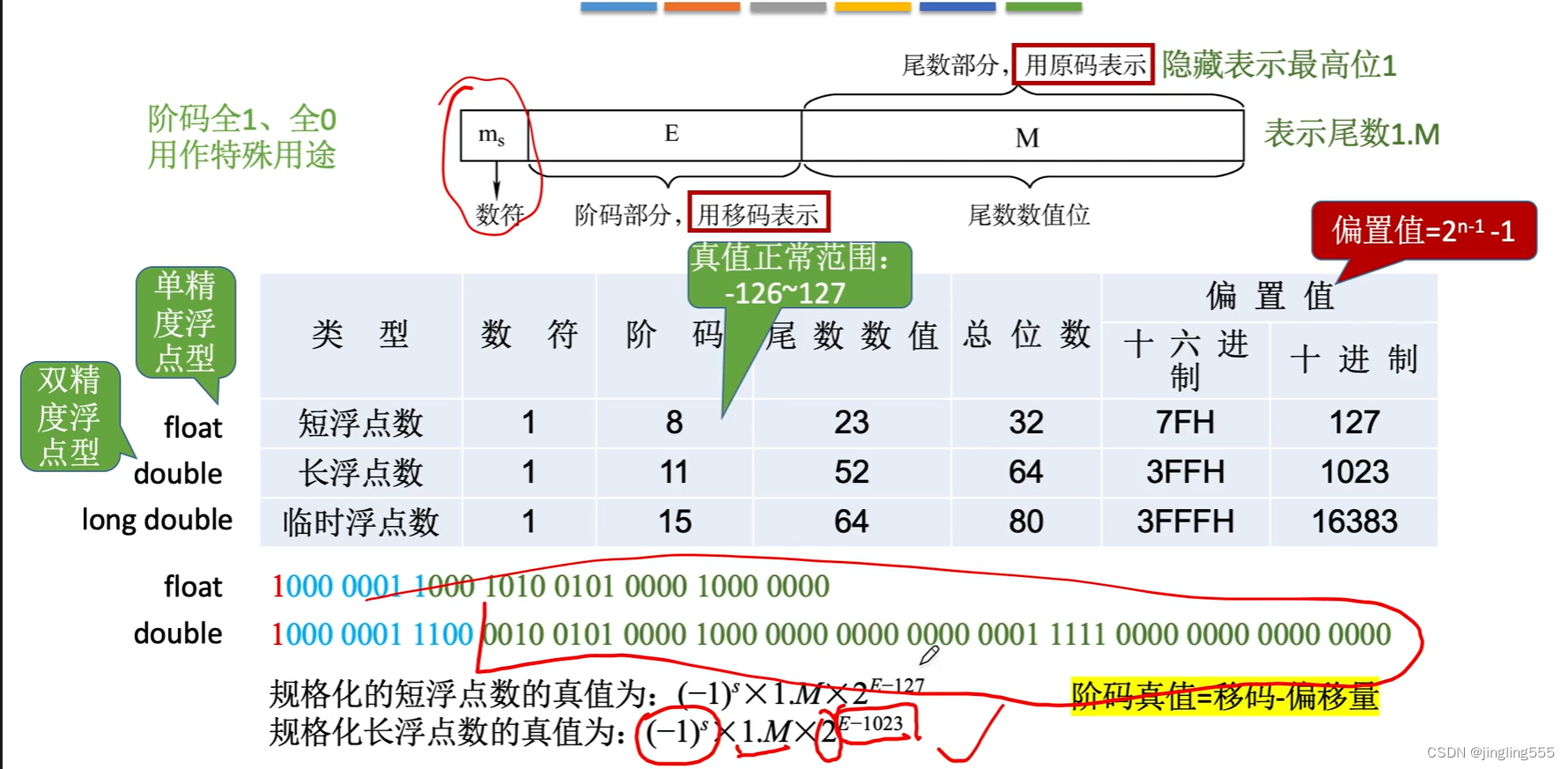


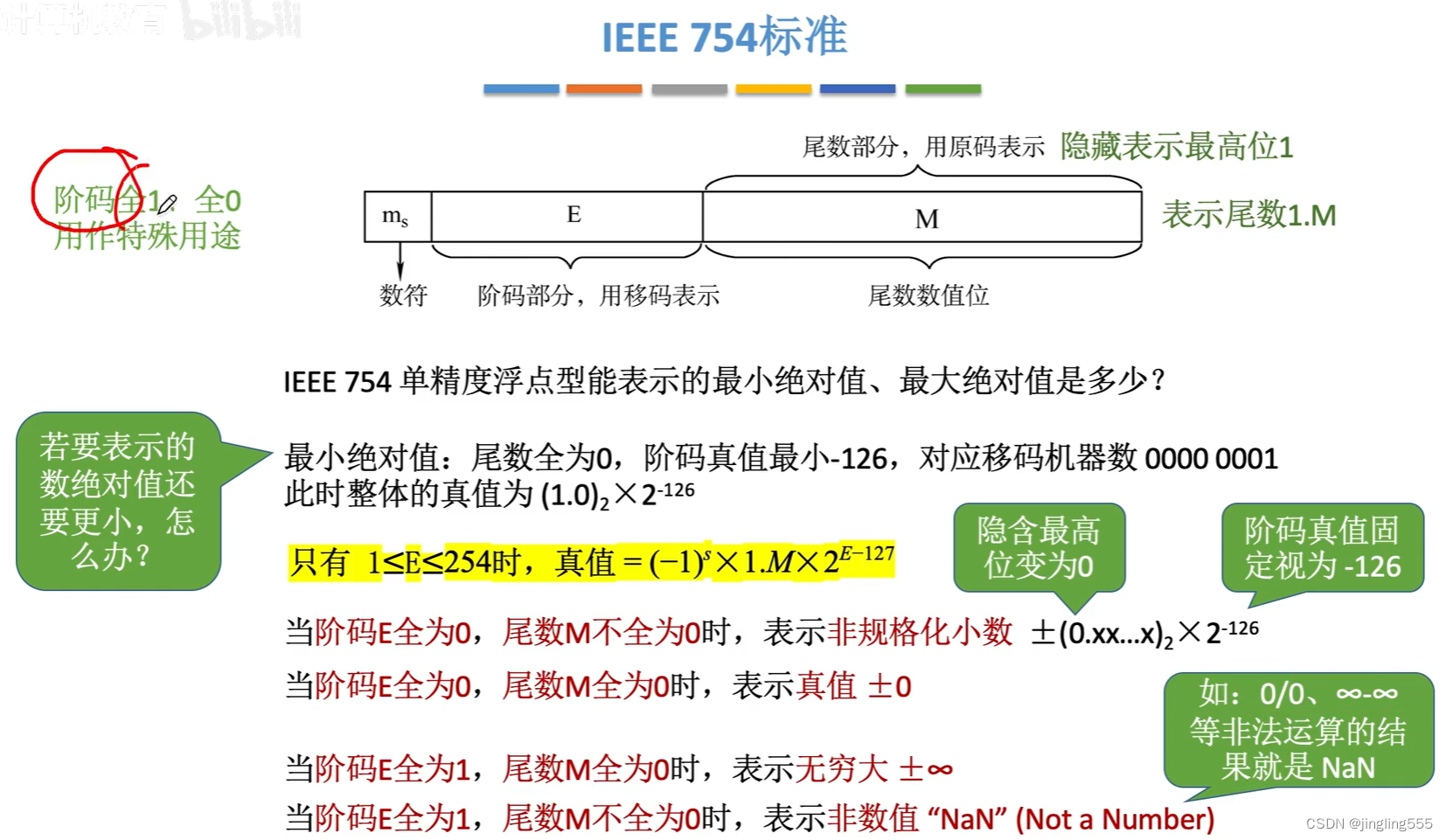
总结:
浮点数的运算
浮点数的加减运算:

浮点数的加减运算--舍入:
强制类型转换: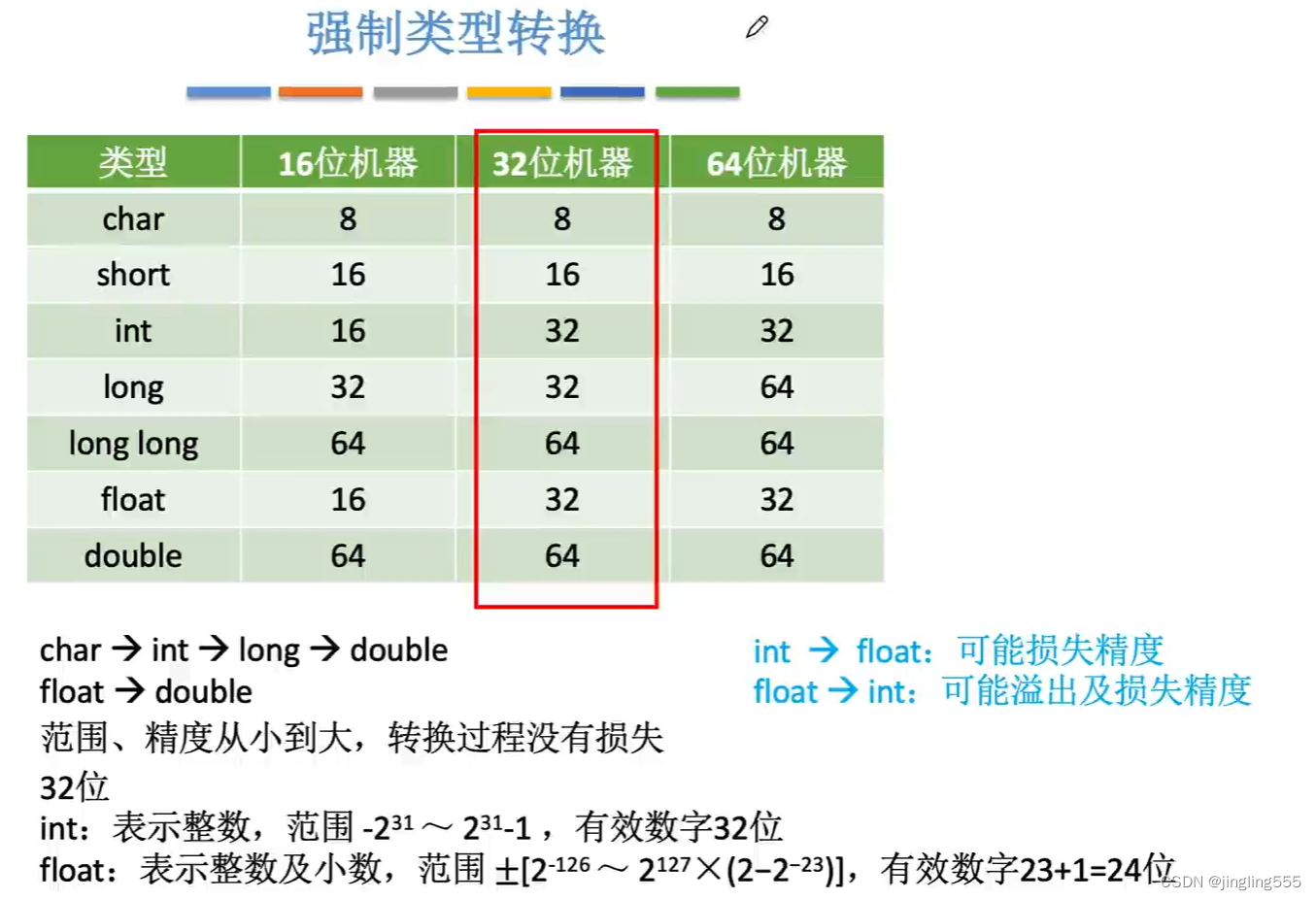
总结: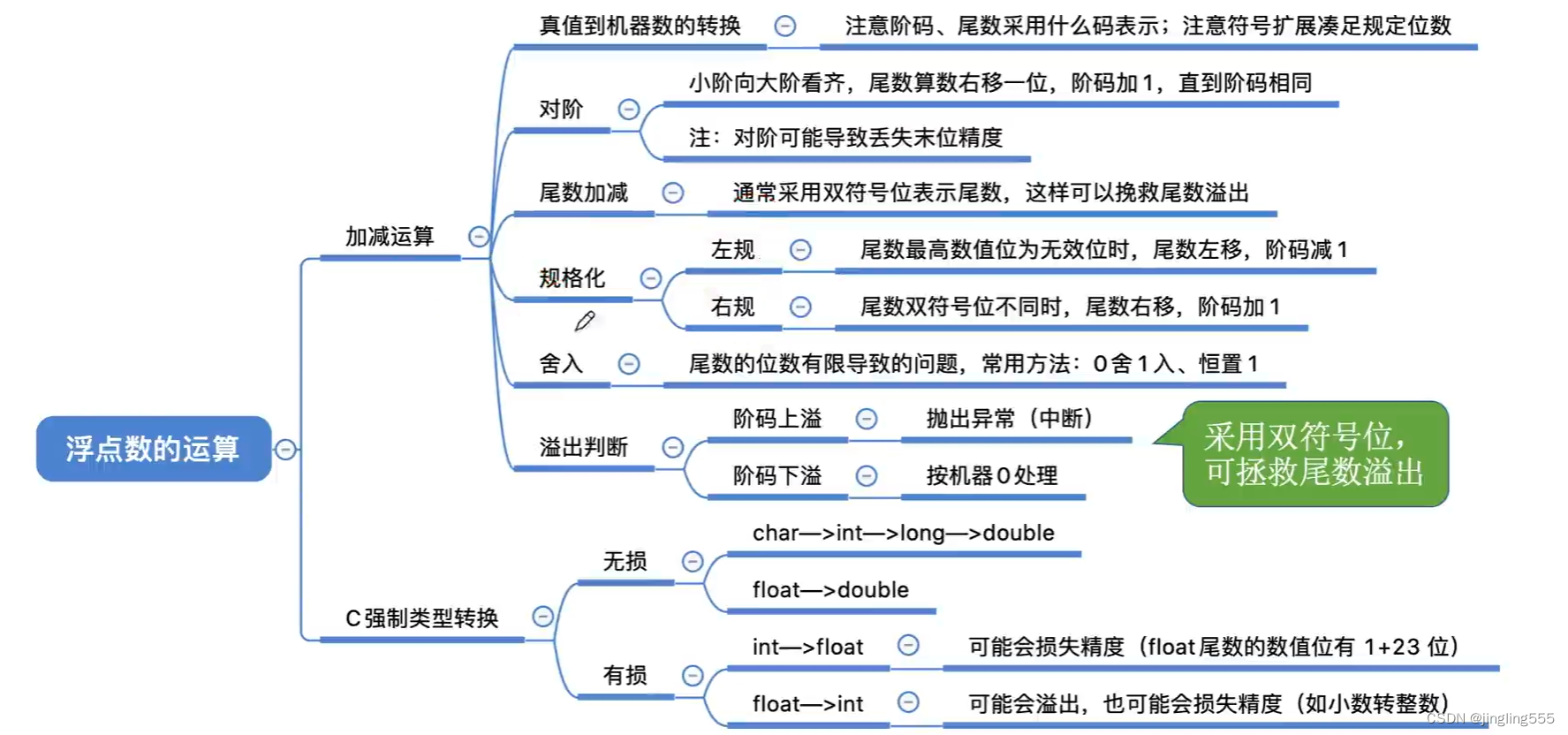
相关文章:

考研408 | 【计算机组成原理】 数据的表示和运算
进位计数制 十进制计数法: 推广:r进制计数法 任意进制-->十进制: 二进制<-->八进制、十六进制: 各种进制的常见书写方式: 十进制-->任意进制: 十进制-->二进制(拼凑法ÿ…...
【小沐学NLP】AI辅助编程工具汇总
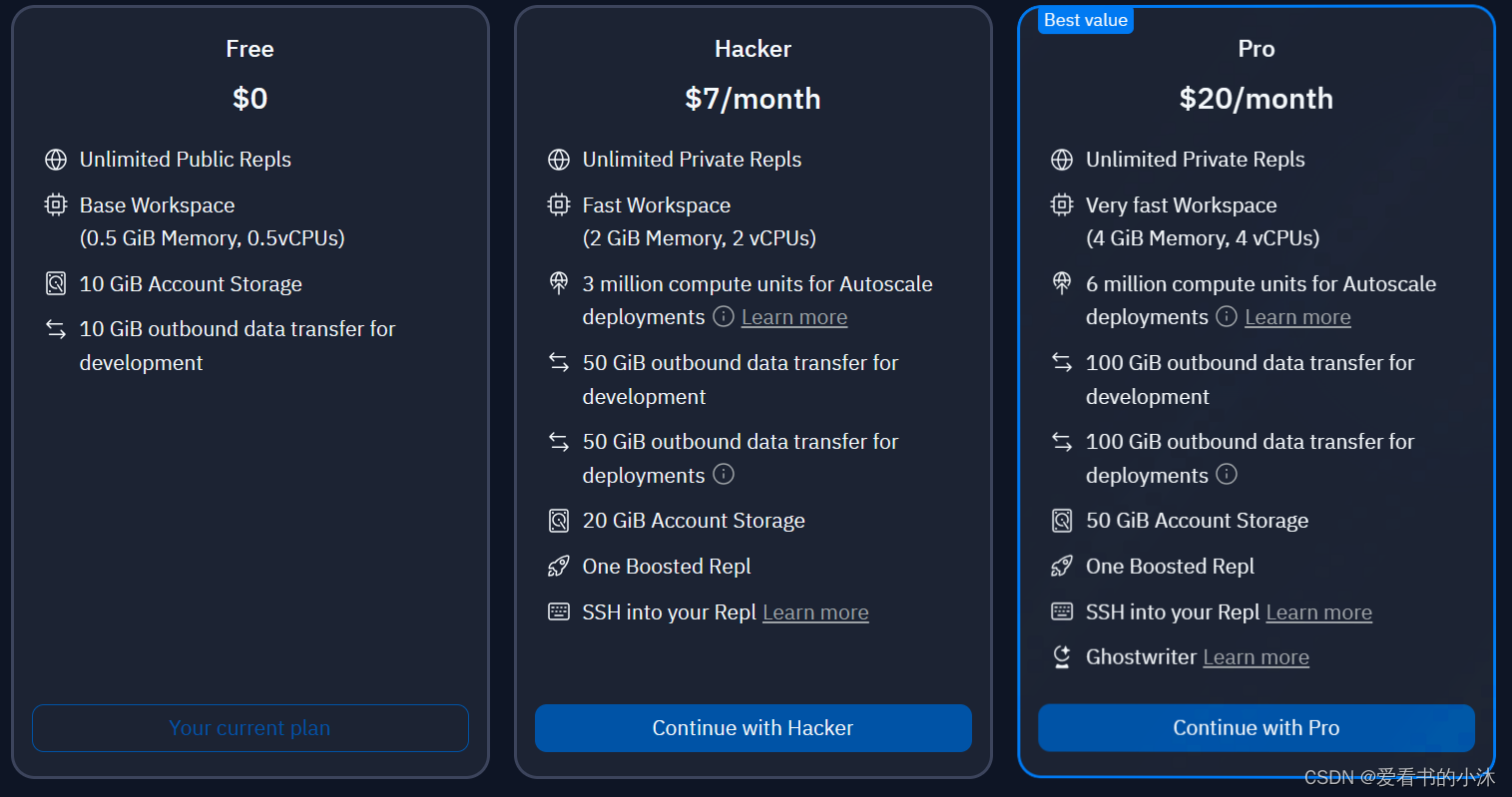
文章目录 1、简介2、国内2.1 aiXcoder2.1.1 工具特点2.1.2 部署方式2.1.3 使用费用2.1.4 代码测试2.1.4.1 代码搜索引擎2.1.4.2 在线体验 2.2 CodeGeeX2.2.1 工具特点2.2.2 部署方式2.2.3 使用费用2.2.4 代码测试 2.3 Alibaba Cloud AI Coding Assistant(cosy&#…...
)
linux动态扩容系统盘(非lvm磁盘)
查看磁盘状态 执行df -Th查看磁盘情况 [rootiotdbtest1 ~]# df -Th Filesystem Type Size Used Avail Use% Mounted on devtmpfs devtmpfs 7.7G 0 7.7G 0% /dev tmpfs tmpfs 7.7G 0 7.7G 0% /dev/shm tmpfs tmpfs …...

Gitlab仓库部署
Gitlab仓库部署 一、Gitlab的概述1、gitlab介绍2、gitlab主要功能3、gitlab和github的区别 二、部署环境1、安装依赖环境2、安装Postfix邮箱3、Gitlab优势4、Gitlab工作流程 三、Gitlab部署过程1、Yum安装Gitlab2、配置gitlab站点URL3、启动并访问Gitlab 四、Gitlab具体操作1、…...
Day46:项目-购物车案例
购物车案例 准备工作 首页默认加载,其余页面懒加载 调用defineStore方法构建store 入口main做对应配置,找指南,快速开始,把elementplus引入进来 import { createApp } from "vue"; import { createPinia } from &qu…...
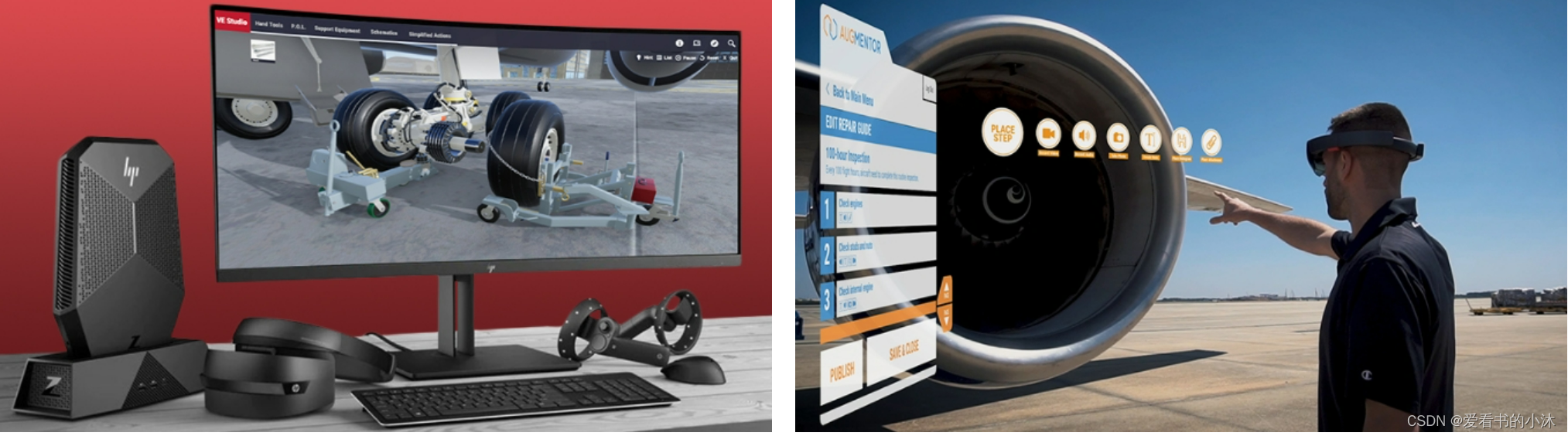
【小沐学CAD】嵌入式UI开发工具:GL Studio
文章目录 1、简介2、软件功能3、应用行业3.1 航空3.2 汽车3.3 防御3.4 工业3.5 电力与能源3.6 医疗3.7 空间3.8 科技 结语 1、简介 https://disti.com/gl-studio/ DiSTI 是 HMI 软件、虚拟驾驶舱、仪表、信息娱乐、集群显示器和嵌入式 UI 解决方案的领先提供商。 而它的GL Stu…...
Python:Tornado框架之获取get和post的传参
一、获取get方式传参 import tornado.ioloop #导入tornado包 import tornado.web class MainHandle(tornado.web.RequestHandler):def get(self,id): #定义请求函数self.write("Hello %s!" %id)apptornado.web.Application([ #定义应用配置函数(r"/…...

JSON和全局异常处理
目录 1️⃣JSON 一、什么是json? 二、与javascript的关系 三、语法格式 四、注意事项 五、总结 六,使用json 1导入pom.xml依赖 2.配置spring-mvc.xml 3. ResponseBody注解使用 创建一个web层控制器 编写ClazzBiz 实现接口 测试: …...

骨传导耳机有害处吗、骨传导耳机真的不好用吗?
骨传导耳机没有害处。 骨传导耳机是通过将声音传递到颅骨,再由颅骨传递到内耳,从而达到听声音的效果,与传统的耳机不同。 因此,骨传导耳机不会直接对人的身体健康、耳朵产生压力和损伤,也不会影响耳道和中耳的正常功能…...

第一类曲面积分:曲面微元dσ与其投影面积微元dxdy之间的关系推导
第一类曲面积分:曲面微元dσ与其投影面积微元dxdy之间的关系推导 本篇博客精简自本人关于曲面积分的博客:详情见:曲面积分(Surface Integral) 曲面参数化(曲面上的每个点都使用起点为原点、终点为该曲面上的点的向量表示&#x…...

vue学习之Font Awesome图标
官方文档 https://fontawesome.com.cn/v5 Font Awesome 安装 cnpm install font-awesome/src/main.js 引入css import Vue from vue; import ElementUI from element-ui; import element-ui/lib/theme-chalk/index.css; import App from ./App.vue;...

mysql内连接与外连接详解
内连接与外连接 内连接外连接 在数据库中,连接操作是一种把两个或者多个表的记录组合在一起的操作,常用的有内连接(Inner Join)、外连接(Outer Join)等。 内连接 内连接(Inner Join࿰…...

在Mujoco环境下详细实现PPO算法应用于Humanoid-v2的完整教程
第一部分:介绍 1. 背景介绍 MuJoCo,或称为多关节动力学与控制的物理引擎,已经成为了强化学习中仿真环境的首选工具。其精确的物理仿真和高效的速度使得研究者可以在这个环境下测试和验证各种算法。PPO,即近端策略优化,是一种深度强化学习中的策略优化方法。它解决了TRPO…...
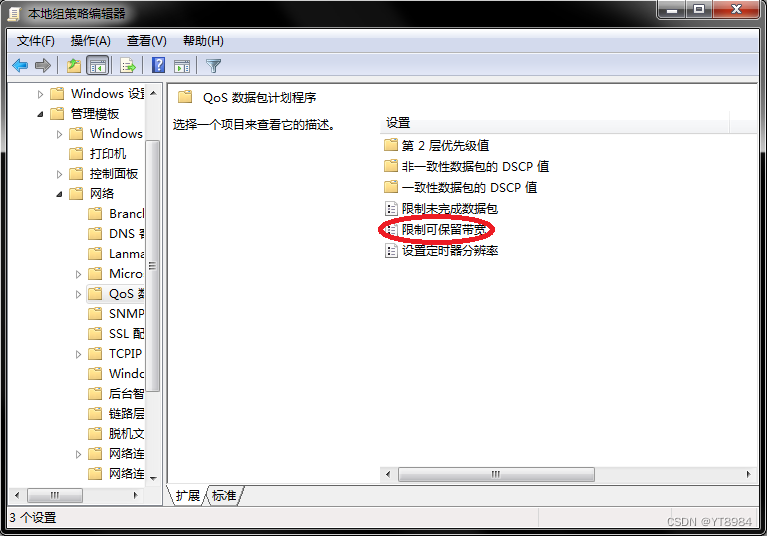
怎么给网络加速
首先,按winr,调出运行窗口。 输入cmd,回车,再输入gpedit.msc,调出本地组策略编辑器。 点击计算机配置下的管理模版。 再点击网络。 再点击Qos数据包计划程序。 再点击限制可保留宽带。 选择已启用,再把带宽…...
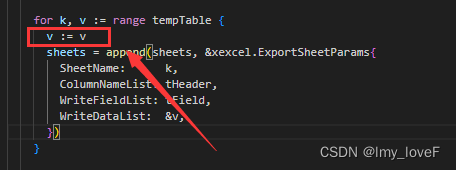
golang for循环append的数据重复
原因,因为使用了& 需要增加一行,问题解决...
趣谈网络协议_1
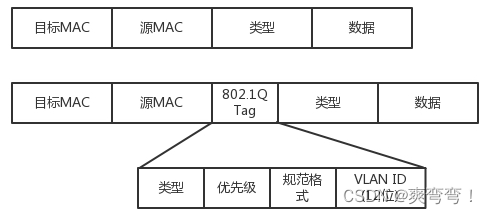
趣谈网络协议_1 第1讲 | 为什么要学习网络协议?第4讲 | DHCP与PXE:IP是怎么来的,又是怎么没的?动态主机配置协议(DHCP) 第5讲 | 从物理层到MAC层:如何在宿舍里自己组网玩联机游戏?第…...

利用WebStorm开发react——本文来自AI创作助手
要在WebStorm中开发React应用程序,请按照以下步骤进行设置: 1.安装Node.js和npm(如果尚未安装)。 2.下载和安装WebStorm。 3.打开WebStorm,并在欢迎界面中选择“Create New Project”。 4.在弹出窗口中,…...

将本地构建的镜像推送到远程镜像库,构建多种系统架构支持的Docker镜像并推送到Docker Hub
目录 推送到 Docker Hub前提:需要在 [Docker Hub](https://hub.docker.com/) 创建账户、创建仓库。1. 创建 Dockerfile 和构建镜像:docker build -t2. 登录到远程镜像库:docker login3. 将镜像标记为远程仓库地址:docker tag4. 推…...

【技术分享】NetLogon于域内提权漏洞(CVE-2020-1472)
一、漏洞介绍 CVE-2020-1472是一个Windows域控中严重的远程权限提升漏洞。攻击者在通过NetLogon(MS-NRPC)协议与AD域控建立安全通道时,可利用该漏洞将AD域控的计算机账号密码置为空,从而控制域控服务器。该漏洞适用于Win2008及后…...

python学习之【模块】
前言 上一篇文章 python学习之【深拷贝】中学习了python中的深浅拷贝学习内容,这篇文章接着学习python中的模块。 什么是模块 在python中,一个文件(以“.py”为后缀名的文件)就叫做一个模块,每一个模块在python里都…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...