《C++ primer plus》精炼(OOP部分)——对象和类(5)
“学习是照亮心灵的火炬,它永不熄灭,永不止息。”
文章目录
- 类的自动和强制类型转换
- 原始类型转换为自定义类型
- 将自定义类型转换为原始类型
类的自动和强制类型转换
原始类型转换为自定义类型
可以用一个参数的构造函数来实现,例如:
class Student{string s;int grade;Student(int i);
}int main(void)
{Student s;s=11;//隐式调用构造函数来实现类型转换s=Student(11);//显式调用构造函数
}
main函数中执行s=11这条语句时,先用构造函数临时构造一个Student变量,再将这个变量赋值给s,最终达到和类型转换相同的效果。
另外,如果声明了explicit关键字,那么不能隐式调用构造函数构造临时变量,只能显式调用:
//两种显式调用构造函数的方法
s=Student(11);
s=(Student)11;
这种转化方式也允许先进行原始类型之间的转换:
//先将double类型的参数转换为int类型,再进行类型转换
s=Student(11.3);
s=(Student)11.3;
s=11.3;
注意,这种构造函数可能引起二义性:
class Student{string s;int grade;Student(int i);Student(double d);
}int main(void)
{Student s;//下面两个函数都会导致二义性s=11;s=Student(11);
}
在这种情况下,11既可以作为int参数调用构造函数,也可以先转换为double参数,然后调用构造函数。
将自定义类型转换为原始类型
将自定义类型转换为其他类型需要特定的转换函数:
operator typename();
转换函数有以下几个特点:
- 转换函数必须是类方法
- 转换函数不能指定返回类型
- 转换函数不能有参数
例如:
class Student{string st;int grade;Student(int i);operator double();
}int main(void)
{Student s;s=11;s=Student(11);double d=s;//调用operator double()函数
}
转换函数也会导致二义性:
class Student{string st;int grade;Student(int i);operator double();operator int();
}int main(void)
{Student s;s=11;s=Student(11);double d=s;//调用operator double()函数,这样不会导致二义性cout<<s;//导致二义性
}
在最后一句中,s既可以转换成double类型,也可以转换成int类型,因此会导致二义性。但是如果进行强制类型转换就不用担心这个问题:
cout<<<(double)s;//不会导致二义性
和构造函数一样,转换函数也可以用explicit关键字来表明必须使用显示类型转换。

我是霜_哀,在算法之路上努力前行的一位萌新,感谢你的阅读!如果觉得好的话,可以关注一下,我会在将来带来更多更全面的知识讲解!
相关文章:

《C++ primer plus》精炼(OOP部分)——对象和类(5)
“学习是照亮心灵的火炬,它永不熄灭,永不止息。” 文章目录 类的自动和强制类型转换原始类型转换为自定义类型将自定义类型转换为原始类型 类的自动和强制类型转换 原始类型转换为自定义类型 可以用一个参数的构造函数来实现,例如ÿ…...

钉钉旧版服务端SDK支持异步方法的升级改造
最近项目中需要对接钉钉,有些钉钉 API 的访问需要使用旧版服务端 SDK 才能搞定,但是这个 SDK 使用的还是 .NET Framework 2.0 框架,不能跨平台部署,也不支持 async\await 的异步操作方法,Nuget 上也有其它用户改造的 .…...
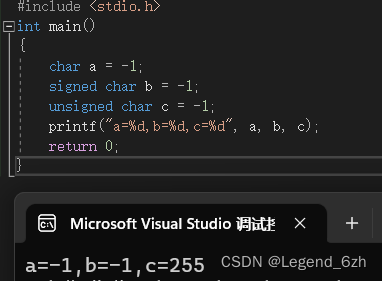
【C语言】【数据存储】用%d打印char类型数据,猜结果是啥
题目代码如下: #include <stdio.h> int main() {char a -1;signed char b-1;unsigned char c-1;printf("a%d,b%d,c%d",a,b,c);return 0; }解题关键: 1.二进制存储:原码,反码,补码 互换 2.截断 3.整型…...

算法——双指针
1658. 将 x 减到 0 的最小操作数 - 力扣(LeetCode) 这道题的重点是,如何用最小的操作数,来使其x变为0——也可以看作是用最少的数据个数,来求和得到x。 ——但是我们可以知道,由于数据是从两端向中间取的…...
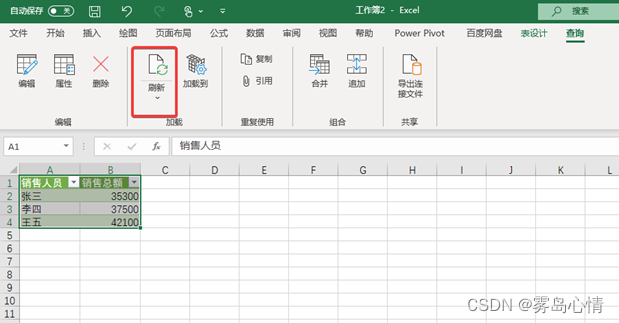
【PowerQuery】Excel的PowerQuery按需刷新
将数据通过PowerQuery 导入进来后,这里将进行数据分组运算,最终的数据计算结果将保存在Excel 表格中,图为销售统计结果。 在Excel中,如果我们希望进行销售统计的手动更新可以使用几种不同的方法来进行刷新: 刷新单一数据连接如果仅仅需要刷新单一数据连接的话我们可以通过…...

Django REST Farmowork初探
1.简介 Django REST framework (简称:DRF)是一个强大而灵活的 Web API 工具。 遵循RESTFullAPI风格,功能完善,可快速开发API平台。 官网文档:https://www.django-rest-framework.org 2. framwork的安装 …...

【flink进阶】-- Flink kubernetes operator 版本升级
目录 1、检查当前 flink kubernetes operator 版本 2、停止生产上正在运行的 flink job 3、升级 CRD...
Linux Ubuntu20.04深度学习环境快速配置命令记录
一、驱动安装 1、更新系统包 sudo apt-get updatesudo apt-get upgrade 2、安装显卡驱动 使用apt方式安装驱动,多数情况不容易成功, 使用一下方法更佳: 1.查看合适显卡的驱动版本 ubuntu-drivers devices NVIDIA GeForce 驱动程序 - …...

信息安全三级真题一
目录 一、单选题 二、填空题 三、综合题 一、单选题 二、填空题 三、综合题 知法懂法,请各位网络安全从业者遵守《网络安全法》、《个人信息保护法》 业%$务*$&联&#系 XHU3ZjUxXHU3ZWRjXHU4ZmQwXHU3ZWY0XHU2ZTE3XHU5MDBmXHU1NmUyXHU5NjFmXHUyMDBiXHU2M…...

RK3568-tftp更新设备树和内核nfs挂载文件系统
1. 注意:需要设备树和内核按以下修改才能支持tftp和nfs。 1.1 修改设备树: diff --git a/arch/arm64/boot/dts/rockchip/OK3568-C-linux.dts b/arch/arm64/boot/dts/rockchip/OK3568-C-linux.dts index 178b4d831..34cb57ffd 100644 --- a/arch/arm64/boot/dts/rockchip/OK…...
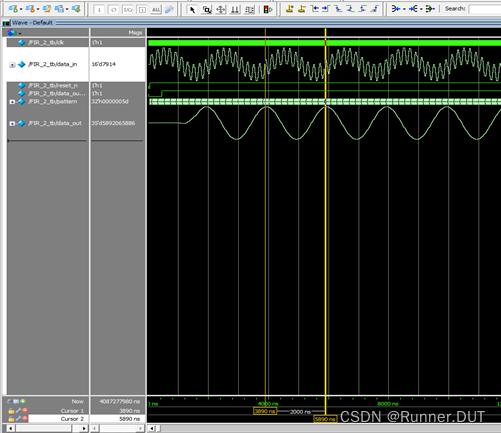
FIR滤波器简述及FPGA仿真验证
数字滤波器的设计,本项目做的数字滤波器准确来说是FIR滤波器。 FIR滤波器(有限冲激响应滤波器),与另一种基本类型的数字滤波器——IIR滤波器(无限冲击响应滤波器)相对应,其实就是将所输入的信号…...
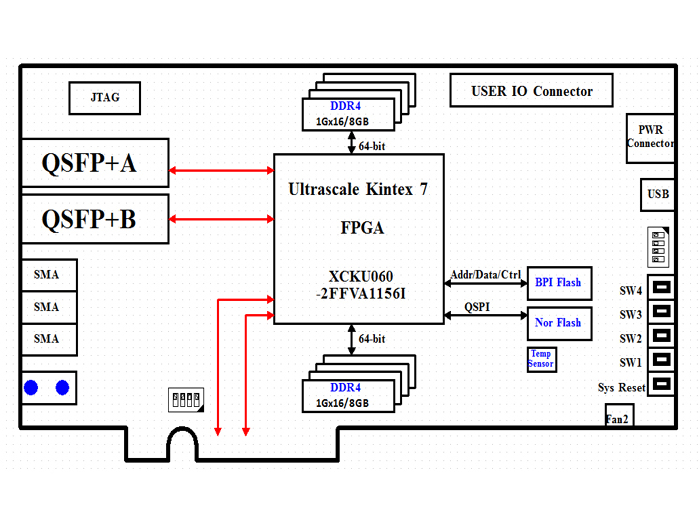
高速信号处理板资料保存:383-基于kintex UltraScale XCKU060的双路QSFP+光纤PCIe 卡设计原理图
基于kintex UltraScale XCKU060的双路QSFP光纤PCIe 卡 一、板卡概述 本板卡系我司自主研发,基于Xilinx UltraScale Kintex系列FPGA XCKU060-FFVA1156-2-I架构,支持PCIE Gen3 x8模式的高速信号处理板卡,搭配两路40G QSFP接口…...
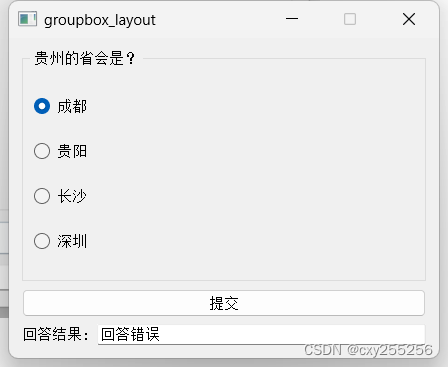
QT:使用分组框、单选按钮、普通按钮、标签、行编辑器、垂直分布、水平分布做一个小项目
widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QRadioButton> //单选按钮 #include <QGroupBox> //分组框 #include <QHBoxLayout> //水平布局 #include <QVBoxLayout> //垂直布局 #include <QPushButton>…...

封装微信小程序隐私信息授权
隐私 代码 html (modal 组件再后面封装有提供) <modal isShow"{{show}}"><view class"privacy-auth-dialog"><view class"title">温馨提示</view><view class"content"><vi…...
【C#】FileInfo类 对文件进行操作
提示:使用FileInfo类时,要引用System.IO命名空间。 using System.IO; FileInfo类 生成文件删除文件移动文件复制文件获取文件名判断文件是否存在属性列表其它常用方法 生成文件 Create():在指定路径上创建文件。 FileInfo myFile new FileIn…...

python中的字符串也是可迭代对象吗?
python中的字符串也是可迭代对象吗? ━━━━━━━━━━━━━━━━━━━━━━ 是的,Python中的字符串是可迭代对象。这意味着你可以像处理列表或元组那样处理字符串。例如,你可以使用for循环遍历字符串中的每个字符,或…...

C++ 图像线特征提取【HoughLinesP算法】
目录 一、函数介绍二、实现步骤三、代码示例一、函数介绍 HoughLinesP:是一种基于Hough变换的直线检测算法。它可以识别图像中的直线,并返回它们的端点坐标。其函数接口如下: cv::HoughLinesP( InputArray src, // 输入图像,必须 8-bit 的灰度图像 OutputArray…...

Stable Diffusion WebUI内存不够爆CUDA Out of memory怎么办?
在我们运行SD的时候,我们经常会爆CUDA Out of memory。 我们应该怎么办呢? 这是因为我们的显存或者内存不够了。 如果你是用cpu来跑图的则表示内存不够,这个时候就需要换个大点的内存了。 如果你是用gpu来跑图的就说明你显存不够用咯,这时候咋办呢? 下面我将一一述说…...

模板学堂|数据可视化仪表板大屏设计流程梳理
DataEase开源数据可视化分析平台于2022年6月正式发布模板市场(https://dataease.io/templates/)。模板市场旨在为DataEase用户提供专业、美观、拿来即用的仪表板模板,方便用户根据自身的业务需求和使用场景选择对应的仪表板模板&a…...
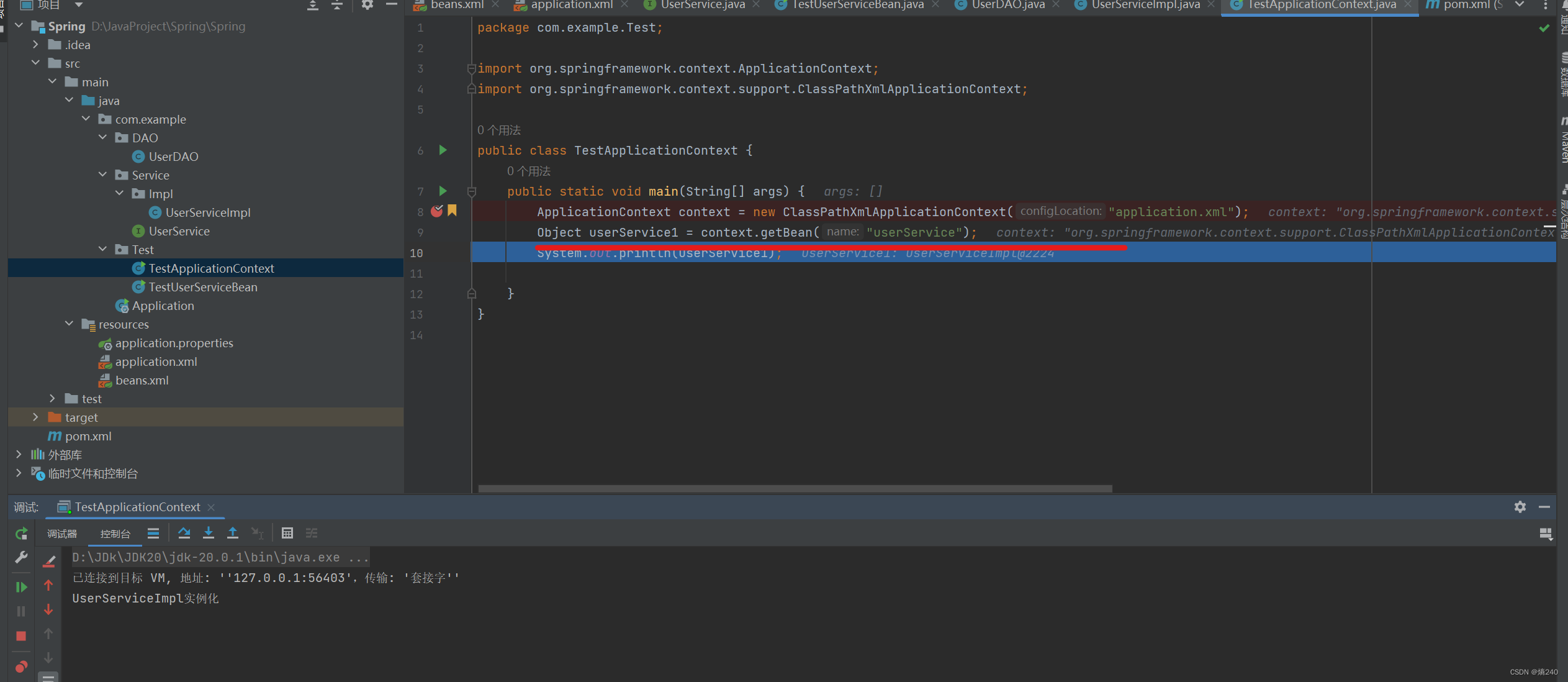
基于Xml方式Bean的配置-Bean的延时加载
SpringBean的配置详解 Bean的延时加载 当lazy-init设置为true时为延时加载,也就是当Spring容器创建的时候,不会立即创建Bean实例,等待用到时再创建Bean实例并储存到单例池中,后续使用该Bean时直接从单例池中获取即可,…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

OCC笔记:TDF_Label中有多个相同类型属性
注:OCCT版本:7.9.1 TDF_Label中有多个相同类型的属性的方案 OCAF imposes the restriction that only one attribute type may be allocated to one label. It is necessary to take into account the design of the application data tree. For exampl…...

Polarctf2025夏季赛 web java ez_check
第一次自己做出一个java,值得小小的记录,polar的java真得非常友好 反编译jar包,一眼就看到有个/deserialize 路由,接受base64的序列化数据,base64解码后 经过一次kmp检查,再由SafeObjectInputStream来反序列…...

vue3+el-table 利用插槽自定义数据样式
<el-table-column label"匹配度" prop"baseMatchingLevel"><template #default"scope"><div :style"{ color: scope.row.baseMatchingLevel > 0.8 ? #00B578 : #FA5151 }">{{ scope.row.baseMatchingLevel }}&l…...

论文阅读笔记——Large Language Models Are Zero-Shot Fuzzers
TitanFuzz 论文 深度学习库(TensorFlow 和 Pytorch)中的 bug 对下游任务系统是重要的,保障安全性和有效性。在深度学习(DL)库的模糊测试领域,直接生成满足输入语言(例如 Python )语法/语义和张量计算的DL A…...

Selenium4+Python的web自动化测试框架
一、什么是Selenium? Selenium是一个基于浏览器的自动化测试工具,它提供了一种跨平台、跨浏览器的端到端的web自动化解决方案。Selenium主要包括三部分:Selenium IDE、Selenium WebDriver 和Selenium Grid。 Selenium IDE:Firefo…...
