Matlab--微积分问题的计算机求解
目录
1.单变量函数的极限问题
1.1.公式例子
1.2.对应例题 1
2.多变量函数的极限问题
3.函数导数的解析解
4.多元函数的偏导数
5.Jacobian函数
6.Hessian矩阵
7.隐函数的偏导
8.不定积分问题的求解
9.定积分的求解问题
10. 多重积分的问题求解
1.单变量函数的极限问题
1.1.公式例子
%%
%3.1.1.单变量函数的极限
%直接趋近
syms x;
y=2*x+2;
L=limit(y,x,2)
%左右趋近
L1=limit(y,x,2,'left')
L2=limit(y,x,2,'right')1.2.对应例题 1
%%
%例题1
syms x;
y=(exp(x^3)-1)/(1-cos(sqrt(x-sin(x))))
limit(y,x,0,'right')1.3. 对应例题2
%%
%例题2
syms t;
f=tan(t);
L1=limit(f,t,pi/2,'left')
L2=limit(f,t,pi/2,'right')
%L1 =Inf L2 =-Inf 2.多变量函数的极限问题
%多变量函数的极限
%需要嵌套使用limit()函数
%L=limit(limit(f,y,y0),x,x0)
syms x y a;
f=exp(-1/(y^2+x^2))*sin(x)^2/x^2*(1+1/y^2)^(x+a^2*y^2)
L=limit(limit(f,x,1/sqrt(y)),y,inf)3.函数导数的解析解
%%
%函数导数的解析解
%函数的导数和高阶导数
%y=diff(fun,x) && y=diff(fun,x,n)
syms x;
f=sin(x)/(x^2+4*x+3);
f1=diff(f)
x1=0:0.01:5;
y=subs(f,x,x1);
y1=subs(f1,x,x1);
plot(x1,y,x1,y1,':')
saveas(gcf,[ 'C:\Users\Zeng Zhong Yan\Desktop\MATLAB\matlab_code','matalb2', '.png']);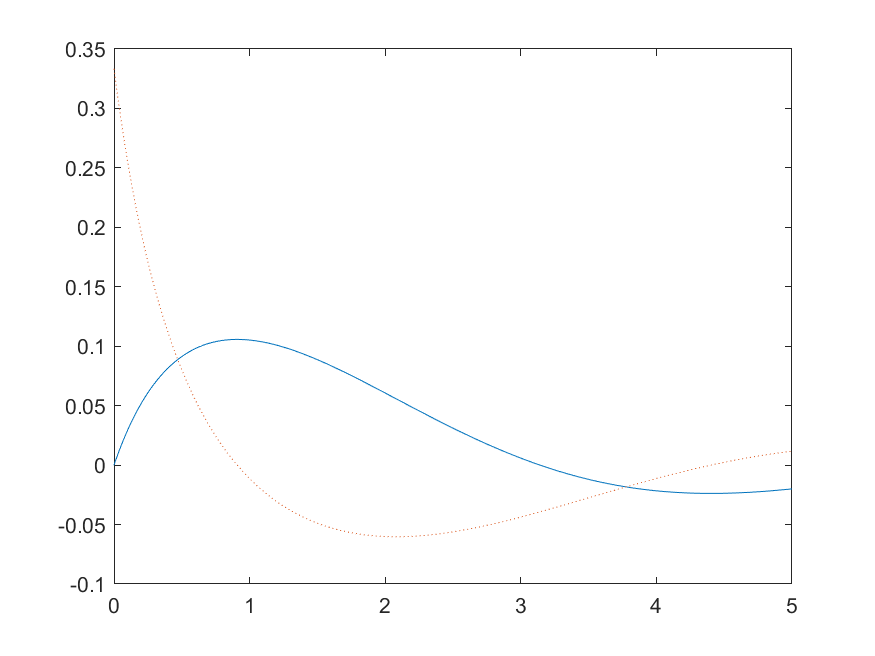
4.多元函数的偏导数
%%
%多元函数的偏导数
%f=diff(diff(f,x,m),y,n)
%f=diff(diff(f,y,n),x,m)
%例题3.8
syms x y;
z=(x^2-2*x)*exp(-x^2-y^2-x*y);
zx=simplify(diff(z,x)),
zy=diff(z,y)[x0,y0]=meshgrid(-3:.2:3,-2:0.2:2);
z=(x0.^2-2*x0).*exp(-x0.^2-y0.^2-x0.*y0);
surf(x0,y0,z),
axis([-3 3 -2 2 -0.7 1.5])
saveas(gcf,[ 'C:\Users\Zeng Zhong Yan\Desktop\MATLAB\','偏导数', '.png']);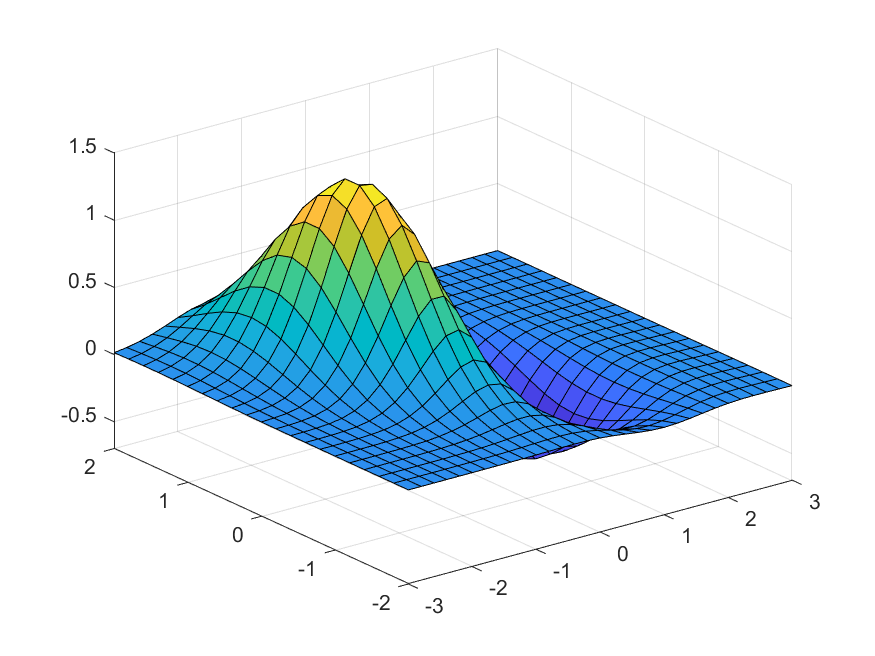
对应例题:
%%
%例题
syms x y z;
f=sin(x^2*y)*exp(-x^2*y-z^2);
f4=diff(diff(diff(f,x,2),y,1),z,1);
f4=simplify(f4)5.Jacobian函数
%%
%Jacobian()函数
syms r theta phi
x=r*sin(theta)*cos(phi);
y=r*sin(theta)*sin(phi);
z=r*cos(theta);
J=jacobian([x;y;z],[r theta phi])6.Hessian矩阵
%%
%Hessian偏导数矩阵
%Hessian矩阵就是两次的雅可比矩阵
H=jacobian(jacobian(f,x),x)对应例题:
%%
%Hessian矩阵例题
syms x y;
f=(x^2-2*x)*exp(-x^2-y^2-x*y);
H=jacobian(jacobian(f,[x,y]),[x,y])7.隐函数的偏导
%%
%隐函数的偏导数
%已知f(x1,x2,x3....x4)=0求解偏导数
F=-diff(f,xj)/diff(f,xi)对应例题:
%%
%隐函数求导例题
syms x y;
f=(x^2-2*x)*exp(-x^2-y^2-x*y);
d=-diff(f,x)/diff(f,y);
d=simplify(d)8.不定积分问题的求解
%%
%不定积分的求解
F=int(fun,x);
%多重嵌套
%F=int(.......int(fun,x))对应例题:
%%
%不定积分例题
syms x;
y=sin(x)/(x^2+4*x+3);
y1=diff(y);
y0=int(y1);
y1,y0
y4=diff(y,4);
y0=int(int(int(int(y4))))9.定积分的求解问题
%%
%定积分与无穷运算
I=int(fun,x,a,b);
I=int(fun,x,a,inf);对应例题1:
%%
syms x;
y=exp(-x^2/2)
I1=int(y,x,0,1.5)
vpa(I1,70)
I1=int(y,x,0,inf)对应例题2:
%%
%定积分例题
f=(-2*x^2+1)/(2*x^2-3*x+1)^2
I=simplify(int(f,x,cos(t),exp(-2*t)))10. 多重积分的问题求解
%%
%多重积分的matlab问题求解
%积分公式差不多,只要注意积分的顺序
syms x y z
k=4*x*z*exp(-x^2*y-z^2);
int(int(int(k,x,0,2),y,0,pi),z,0,pi)
%ans =-(exp(-pi^2) - 1)*(eulergamma + log(4*pi)
相关文章:

Matlab--微积分问题的计算机求解
目录 1.单变量函数的极限问题 1.1.公式例子 1.2.对应例题 1 2.多变量函数的极限问题 3.函数导数的解析解 4.多元函数的偏导数 5.Jacobian函数 6.Hessian矩阵 7.隐函数的偏导 8.不定积分问题的求解 9.定积分的求解问题 10. 多重积分的问题求解 1.单变量函数的极限问题 …...
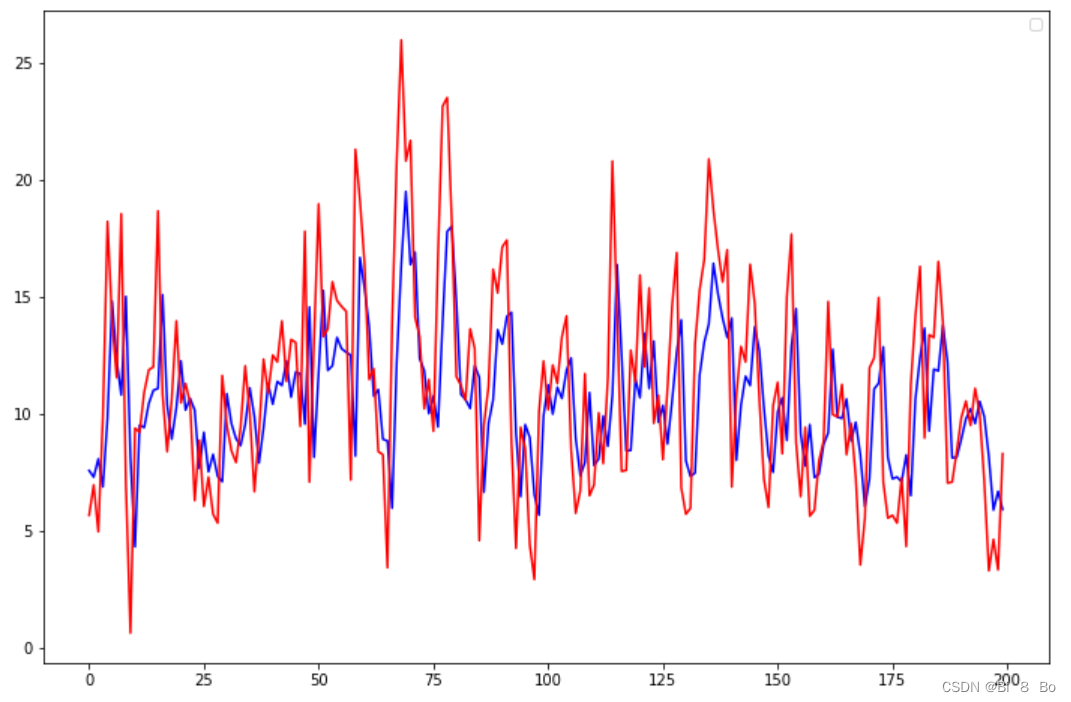
GRU实现时间序列预测(PyTorch版)
💥项目专栏:【深度学习时间序列预测案例】零基础入门经典深度学习时间序列预测项目实战(附代码数据集原理介绍) 文章目录 前言一、基于PyTorch搭建GRU模型实现风速时间序列预测二、时序数据集的制作三、数据归一化四、数据集加载器…...

文本框粘贴时兼容Unix、Mac换行符的方法源码
本篇文章属于《518抽奖软件开发日志》系列文章的一部分。 我在开发《518抽奖软件》(www.518cj.net)的时候,要在文本框粘贴从别处复制来的名单。发现一个问题,就是一些Unix传过来的多行文本,粘贴后都变成了一行。原来&a…...
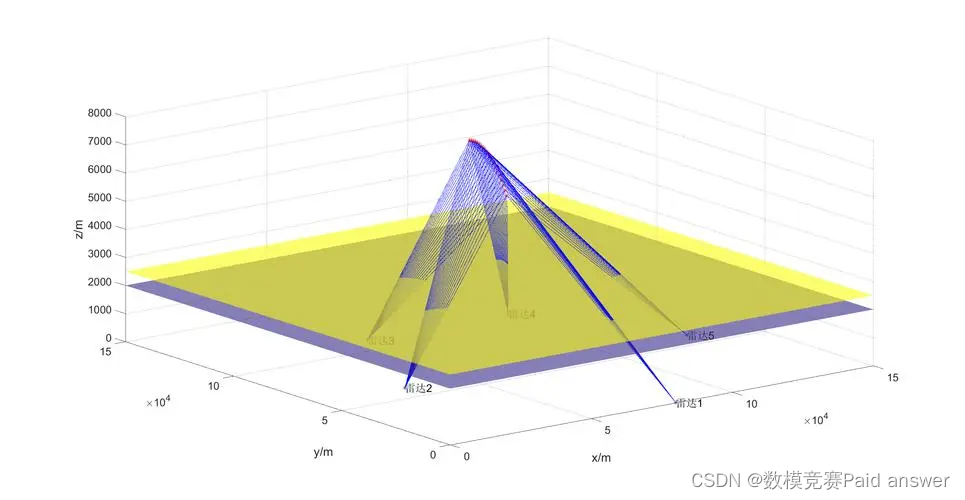
2023年华为杯研究生数学建模竞赛辅导
2023年华为杯研究生数学建模竞赛辅导 各研究生培养单位: 中国研究生数学建模竞赛作为教育部学位管理与研究生教育司指导,中国学位与研究生教育学会、中国科协青少年科技中心主办的“中国研究生创新实践系列大赛”主题赛事之一,是一项面向在校…...
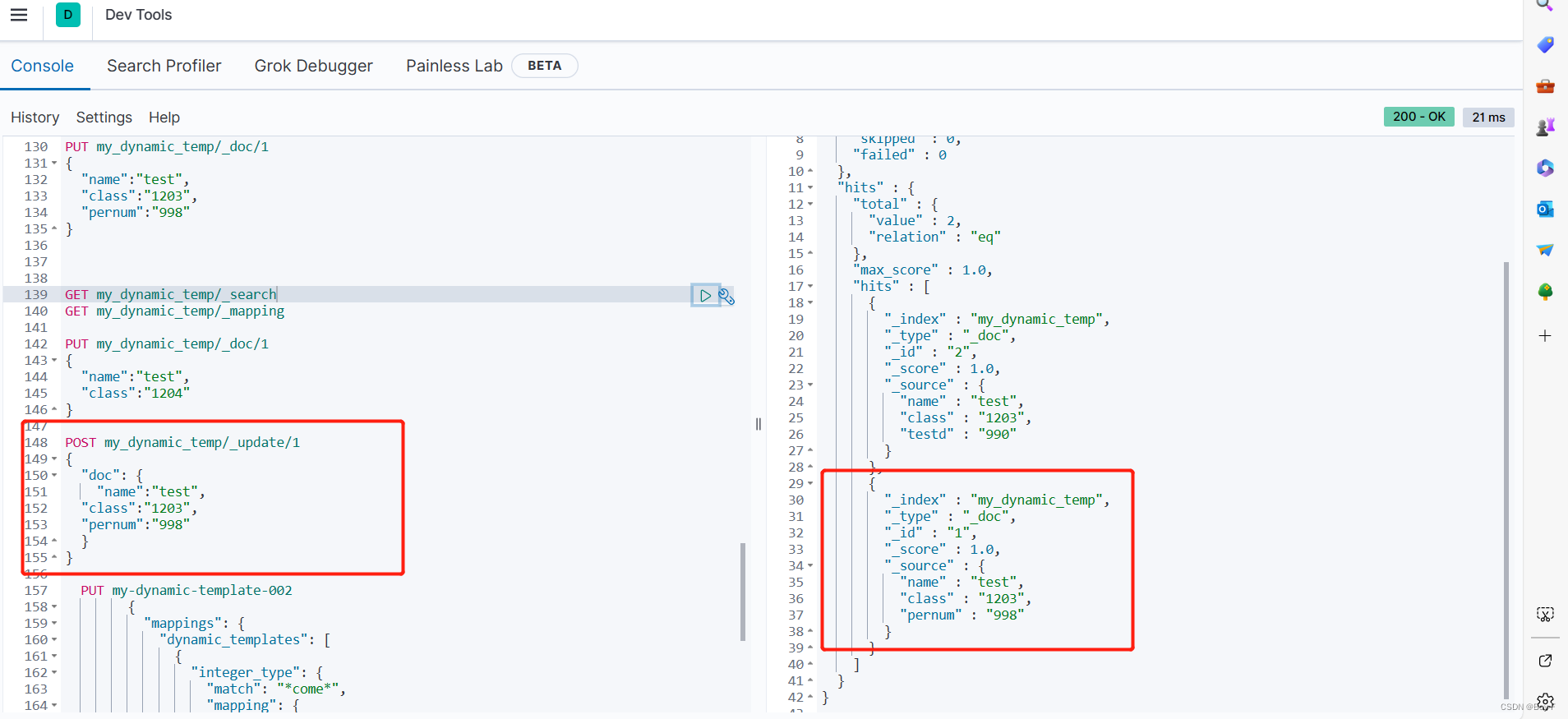
post更新,put相当于删除重新增一条
索引数据 //删除后新增 PUT my_dynamic_temp/_doc/1 { “name”:“test”, “class”:“1204” } //覆盖更新 POST my_dynamic_temp/_update/1 { “doc”: { “name”:“test”, “class”:“1203”, “pernum”:“998” } }...

python责任链模式
责任链模式是一种行为设计模式,它允许你将请求沿着处理者链进行传递,直到有一个处理者能够处理它为止。在Python中,你可以使用多线程来实现责任链模式的框架。 首先,你需要定义一个基础的处理者类,它包含处理请求的方…...
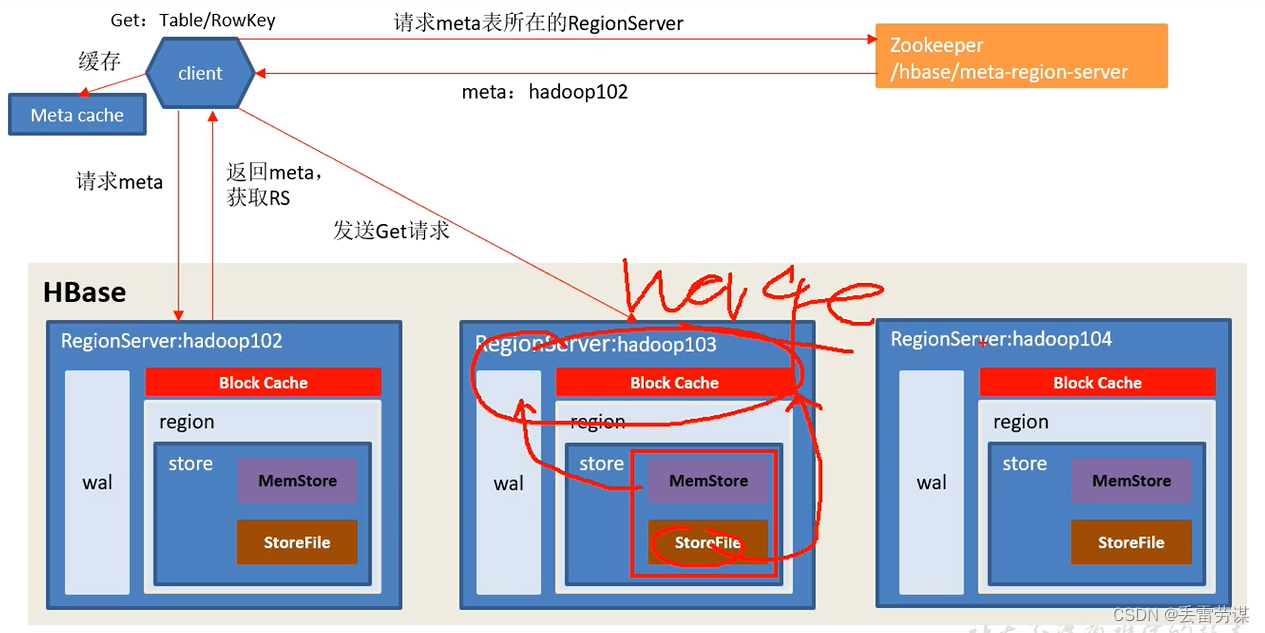
大数据技术准备
Hbase:HBase 底层原理详解(深度好文,建议收藏) - 腾讯云开发者社区-腾讯云 Hbase架构图 同一个列族如果有多个store,那么这些store在不同的region Hbase写流程(读比写慢) MemStore Flush Hbas…...

【力扣周赛】第 362 场周赛(⭐差分匹配状态压缩DP矩阵快速幂优化DPKMP)
文章目录 竞赛链接Q1:2848. 与车相交的点解法1——排序后枚举解法2——差分数组⭐差分数组相关题目列表📕1094. 拼车1109. 航班预订统计2381. 字母移位 II2406. 将区间分为最少组数解法1——排序贪心优先队列解法2——差分数组 2772. 使数组中的所有元素…...
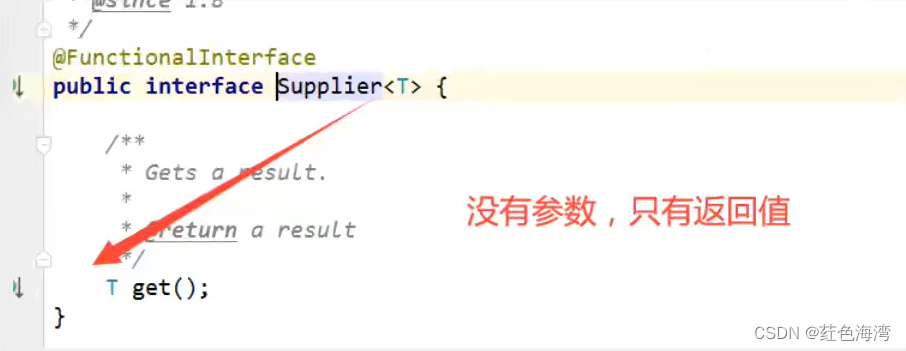
四大函数式接口(重点,必须掌握)
新时代程序员必须要会的 :lambda表达式、链式编程、函数式接口、Stream流式计算 什么是函数式接口 1.函数型接口 package com.kuang.function;import java.util.function.Function;/*** Function函数型接口 有一个输入参数,有一个输出* 只要是函数式接口…...
2023Web前端逻辑面试题
1、现有9个小球,已知其中一个球比其它的重,如何只用天平称2次就找出该球? ①把9个球分成三份,三个一份; ②拿出其中两份进行称量;会分为两种情况 若拿出的两份小球称量结果,重量相等;…...

uniapp中git忽略node_modules,unpackage文件
首先在当前项目的命令行新建.gitignore文件: touch .gitignore再在编辑器中打开该文件,并在该文件中加入需要忽略的文件名: node_modules/ .project unpackage/ .DS_Store 提示:如果以前提交过unpackage文件的话,需…...

Json-Jackson和FastJson
狂神: 测试Jackson 纯Java解决日期格式化 设置ObjectMapper FastJson: 知乎:Jackson使用指南 1、常见配置 方式一:yml配置 spring.jackson.date-format指定日期格式,比如yyyy-MM-dd HH:mm:ss,或者具体的…...

RK3588 点亮imx586摄像头
一.硬件原理图 mipi摄像头硬件确认点: 1.供电:5V,2.8V,1.2V,1.8V,reset脚(硬拉3.3,上电的时候从低到高),pwron脚外接 3.3V。 2,时钟:MCLKOUT是2…...
C++---继承
继承 前言继承的概念及定义继承的概念继承定义继承关系和访问限定符 基类和派生类对象赋值转换继承中的作用域派生类的默认成员函数继承与友元继承与静态成员**多重继承**多继承下的类作用域菱形继承虚继承使用虚基类 支持向基类的常规类型转换 前言 在需要写Father类和Mother…...

使用新版Maven-mvnd快速构建项目
目前我们项目的构建方式多数是 maven、gradle,但是 maven 相对 gradle 来说,构建速度较慢,特别是模块相对较多的时候,构建速度更加明显。但是我们将项目由 maven 替换为 gradle 相对来说会比较麻烦,成本较高。于是我们…...
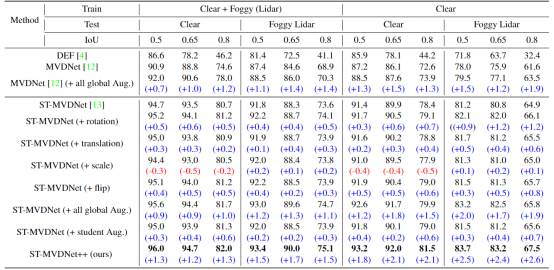
【ICASSP 2023】ST-MVDNET++论文阅读分析与总结
主要是数据增强的提点方式。并不能带来idea启发,但对模型性能有帮助 Challenge: 少有作品应用一些全局数据增强,利用ST-MVDNet自训练的师生框架,集成了更常见的数据增强,如全局旋转、平移、缩放和翻转。 Contributi…...
MySQL 面试题——MySQL 基础
目录 1.什么是 MySQL?有什么优点?2.MySQL 中的 DDL 与 DML 是分别指什么?3.✨数据类型 varchar 与 char 有什么区别?4.数据类型 BLOB 与 TEXT 有什么区别?5.DATETIME 和 TIMESTAMP 的异同?6.✨MySQL 中 IN …...
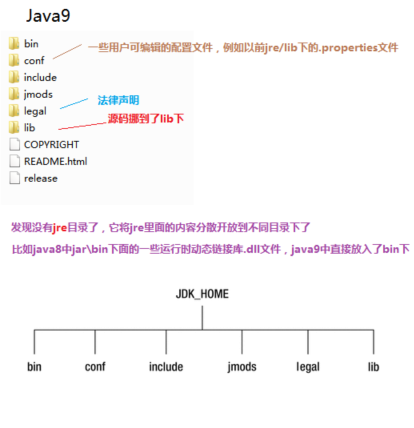
JDK9特性——概述
文章目录 引言JDK9特性概述JDK9的改变JDK和JRE目录变化总结 引言 JAVA8 及之前,版本都是特性驱动的版本更新,有重大的特性产生,然后进行更新。 JAVA9开始,JDK开始以时间为驱动进行更新,以半年为周期,到时…...

征战开发板从无到有(三)
接上一篇,翘首已盼的PCB板子做好了,管脚约束信息都在PCB板上体现出来了,很满意,会不会成为爆款呢,嘿嘿,来,先看看PCB裸板美图 由于征战开发板电路功能兼容小梅哥ACX720,大家可以直…...
Linux设备树详细学习笔记
参考文献 参考视频 开发板及程序 原子mini 设备树官方文档 设备树的基本概念 DT:Device Tree //设备树 FDT: Flattened Device Tree //开放设备树,起源于OpenFirmware (所以后续会见到很多OF开头函数) dts: device tree source的缩写 //设备树源码 dtsi: device …...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...
