Java手写最大子数组和算法(如Kadane算法)和最大子数组和算法(如Kadane算法)应用拓展案例
Java手写最大子数组和算法(如Kadane算法)和最大子数组和算法(如Kadane算法)应用拓展案例
1. 算法思维导图
以下是使用mermaid代码表示的Kadane算法的实现原理:
2. 该算法的手写必要性和市场调查
手写最大子数组和算法的必要性在于理解算法的原理和实现细节,以及在实际应用中能够根据需求进行定制化的修改。市场调查显示,Kadane算法是解决最大子数组和问题的常用算法之一,广泛应用于数据分析、金融领域、图像处理等多个领域。
3. 该算法的实现详细介绍和步骤
Kadane算法是一种动态规划算法,用于求解给定数组中最大子数组的和。以下是该算法的详细步骤:
- 初始化当前子数组的最大和为0,并初始化全局最大和为负无穷大。
- 遍历数组中的每个元素。
- 判断当前子数组和是否大于0:
- 如果大于0,更新当前子数组和为当前元素值。
- 如果小于等于0,将当前元素值加到当前子数组和上。
- 判断当前子数组和是否大于全局最大和:
- 如果大于全局最大和,更新全局最大和为当前子数组和。
- 如果小于等于全局最大和,继续遍历下一个元素。
- 重复步骤2-4,直到遍历完所有元素。
- 返回全局最大和作为最大子数组的和。
4. 该算法的手写实现总结和思维拓展
手写实现Kadane算法能够加深对算法原理和实现细节的理解,同时也能够提高编程能力和算法设计能力。思维拓展方面,可以尝试对该算法进行优化,例如使用分治法或并行计算来加速最大子数组和的计算过程。
5. 该算法的完整代码
以下是Java语言实现的Kadane算法的完整代码,每行代码都有注释说明:
public class KadaneAlgorithm {public static int maxSubArraySum(int[] nums) {int maxSum = Integer.MIN_VALUE; // 初始化全局最大和为负无穷大int currentSum = 0; // 初始化当前子数组的最大和为0for (int i = 0; i < nums.length; i++) {if (currentSum > 0) { // 当前子数组和大于0currentSum = nums[i]; // 更新当前子数组和为当前元素值} else {currentSum += nums[i]; // 将当前元素值加到当前子数组和上}if (currentSum > maxSum) { // 当前子数组和大于全局最大和maxSum = currentSum; // 更新全局最大和为当前子数组和}}return maxSum; // 返回全局最大和作为最大子数组的和}public static void main(String[] args) {int[] nums = {-2, 1, -3, 4, -1, 2, 1, -5, 4};int maxSum = maxSubArraySum(nums);System.out.println("The maximum subarray sum is: " + maxSum);}
}
6. 该算法的应用前景调研
Kadane算法作为解决最大子数组和问题的经典算法,在实际应用中具有广泛的前景。以下是对该算法的应用前景的调研结果:
- 数据分析领域:Kadane算法可以用于求解时间序列数据中的最大子序列和,从而帮助分析师发现数据中的趋势和异常情况。
- 金融领域:Kadane算法可以用于计算股票价格序列中的最大收益,帮助投资者制定买入和卖出策略。
- 图像处理领域:Kadane算法可以用于图像处理中的边缘检测和特征提取等任务,通过计算图像中的最大子数组和来定位感兴趣的区域。
7. 该算法的拓展应用案例
以下是Kadane算法的三个拓展应用案例的完整代码,每个步骤的代码都有文字描述:
拓展应用案例1:最大连续乘积子数组
public class MaxProductSubarray {public static int maxProduct(int[] nums) {int maxProduct = nums[0]; // 初始化最大连续乘积为第一个元素int minProduct = nums[0]; // 初始化最小连续乘积为第一个元素int maxResult = nums[0]; // 初始化最大结果为第一个元素for (int i = 1; i < nums.length; i++) {if (nums[i] < 0) { // 当前元素为负数,交换最大连续乘积和最小连续乘积int temp = maxProduct;maxProduct = minProduct;minProduct = temp;}maxProduct = Math.max(nums[i], maxProduct * nums[i]); // 更新最大连续乘积minProduct = Math.min(nums[i], minProduct * nums[i]); // 更新最小连续乘积maxResult = Math.max(maxResult, maxProduct); // 更新最大结果}return maxResult; // 返回最大结果作为最大连续乘积子数组的乘积}public static void main(String[] args) {int[] nums = {-2, 3, -4, 5, -6};int maxProduct = maxProduct(nums);System.out.println("The maximum product of a subarray is: " + maxProduct);}
}
拓展应用案例2:最长连续递增子数组
public class LongestIncreasingSubarray {public static int longestIncreasingSubarray(int[] nums) {int maxLength = 1; // 初始化最长连续递增子数组长度为1int currentLength = 1; // 初始化当前连续递增子数组长度为1for (int i = 1; i < nums.length; i++) {if (nums[i] > nums[i - 1]) { // 当前元素大于前一个元素currentLength++; // 当前连续递增子数组长度加1maxLength = Math.max(maxLength, currentLength); // 更新最长连续递增子数组长度} else {currentLength = 1; // 当前元素不大于前一个元素,重置当前连续递增子数组长度为1}}return maxLength; // 返回最长连续递增子数组长度}public static void main(String[] args) {int[] nums = {1, 3, 5, 2, 4, 6, 8};int maxLength = longestIncreasingSubarray(nums);System.out.println("The length of the longest increasing subarray is: " + maxLength);}
}
拓展应用案例3:最长连续公差子数组
public class LongestArithmeticSubarray {public static int longestArithmeticSubarray(int[] nums) {int maxLength = 2; // 初始化最长连续公差子数组长度为2int currentLength = 2; // 初始化当前连续公差子数组长度为2int difference = nums[1] - nums[0]; // 初始化公差为第一个元素和第二个元素的差for (int i = 2; i < nums.length; i++) {if (nums[i] - nums[i - 1] == difference) { // 当前元素和前一个元素的差等于公差currentLength++; // 当前连续公差子数组长度加1maxLength = Math.max(maxLength, currentLength); // 更新最长连续公差子数组长度} else {difference = nums[i] - nums[i - 1]; // 更新公差为当前元素和前一个元素的差currentLength = 2; // 重置当前连续公差子数组长度为2}}return maxLength; // 返回最长连续公差子数组长度}public static void main(String[] args) {int[] nums = {1, 3, 5, 7, 9, 10, 12, 14};int maxLength = longestArithmeticSubarray(nums);System.out.println("The length of the longest arithmetic subarray is: " + maxLength);}
}
以上是Kadane算法的三个拓展应用案例的完整代码,可以根据需要进行修改和调试。
相关文章:
和最大子数组和算法(如Kadane算法)应用拓展案例)
Java手写最大子数组和算法(如Kadane算法)和最大子数组和算法(如Kadane算法)应用拓展案例
Java手写最大子数组和算法(如Kadane算法)和最大子数组和算法(如Kadane算法)应用拓展案例 1. 算法思维导图 以下是使用mermaid代码表示的Kadane算法的实现原理: #mermaid-svg-rI7hVAVsP1qtjZK7 {font-family:"tr…...

掌握NVM、NRM和NPM:Node.js开发的利器
**掌握NVM、NRM和NPM:Node.js开发的利器** 背景介绍:如何使用NVM:在Windows上安装NVM:在macOS上安装NVM:配置NVM:常用NVM命令: 如何使用NRM:安装NRM:配置全局NRM…...

Nacos 2.2.3 部署到linux
到https://github.com/alibaba/nacos/releases 下载编译后压缩包,如nacos-server-2.2.3.tar.gz这种,里面包含有nacos的jar包,不然启动不了 1.新建并初始化数据库 创建nacos数据库,执行mysql-schema.sql文件,这个文件…...
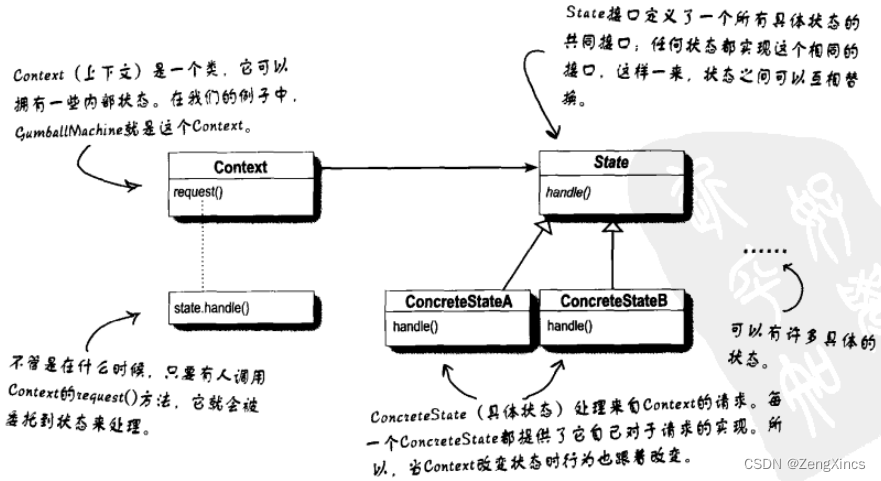
设计模式之十:状态模式
状态模式通过改变对象内部的状态来帮助对象控制自己的行为。 这是一张状态图,其中每个圆圈都是一个状态。 最简单,第一反应的实现就是使用一个变量来控制状态值,并在方法内书写条件代码来处理不同情况。 package headfirst.designpatterns.…...
基本使用指南)
Python 的运算符和语句(条件、循环、异常)基本使用指南
运算符的分类 算数运算符赋值运算符复合赋值运算符比较运算符逻辑运算符 算数运算符 运算符描述实例加1 1 输出结果为 2-减1 - 1 输出结果为 0*乘2 * 2 输出结果为 4/除10 / 2 输出结果为 5//整除9 // 4 输出结果为 2%取余9 % 4 输出结果为 1**指数2 ** 4 输出结果为 16&…...

文心一言 VS 讯飞星火 VS chatgpt (94)-- 算法导论9.2 3题
三、用go语言,给出 RANDOMIZED-SELECT的一个基于循环的版本。 文心一言: 在循环中实现 RANDOMIZED-SELECT 的一个版本可以如下所示。这个版本使用 Go 语言编写,利用随机化来选择一个元素,并在循环中不断地调整选择的元素&#x…...
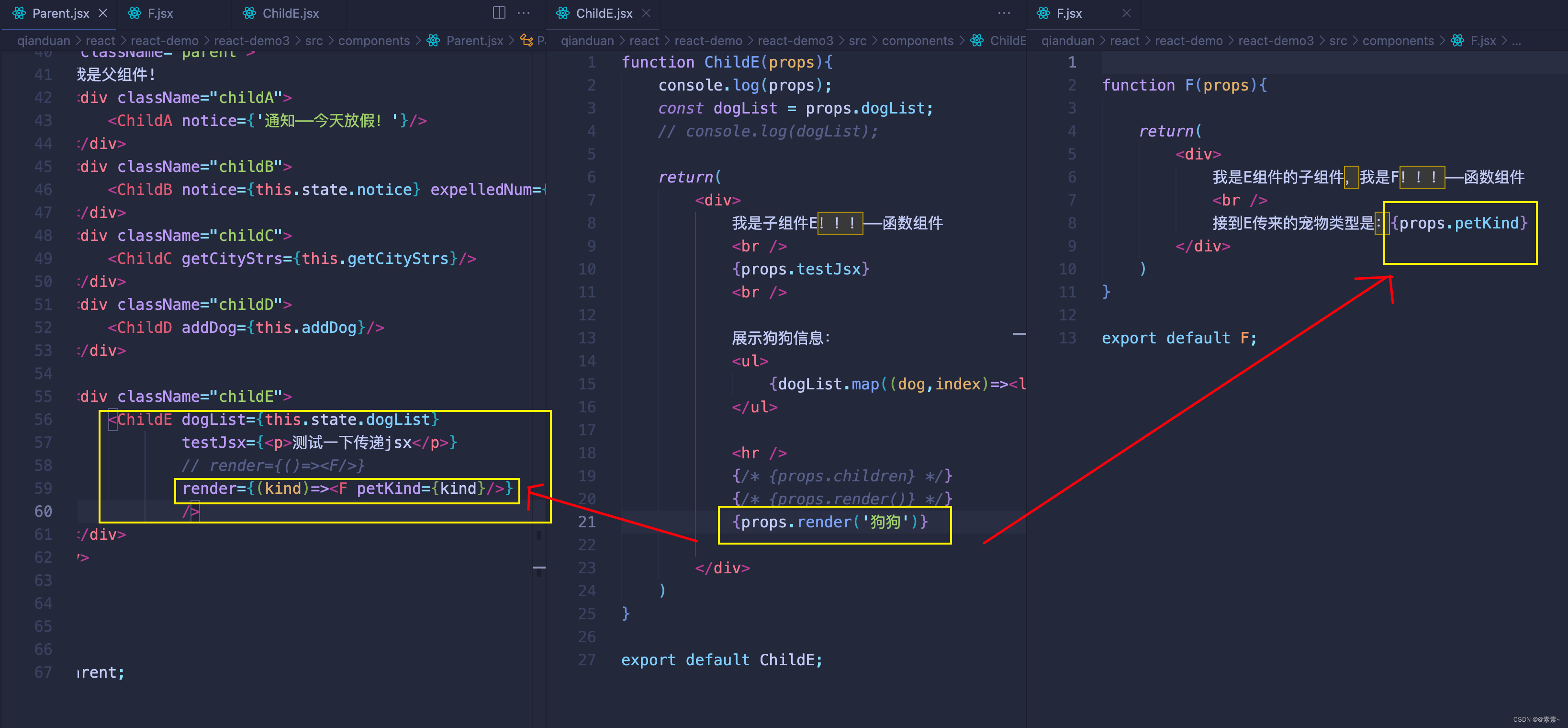
React中组件通信01——props
React中组件通信01——props 1. 父传子——props1.1 简单例子——props1.2 props 可以传递任何数据1.2.1 传递数字、对象等1.2.2 传递函数1.2.3 传递模版jsx 2. 子传父 子传子——props2.1 父传子——传递函数2.2 子传父——通过父传子的函数实现2.3 优化 子传子(…...
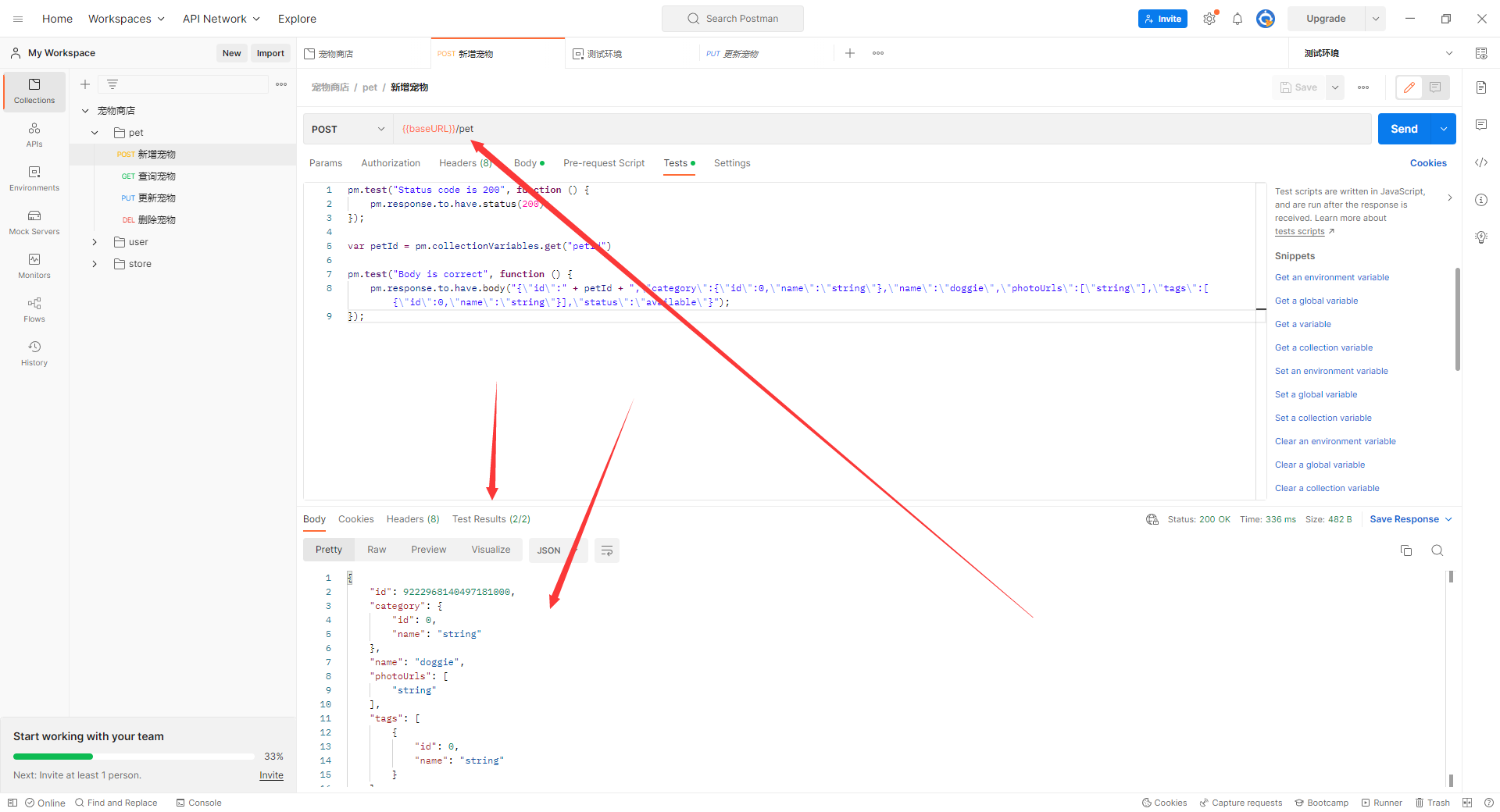
接口测试——接口协议抓包分析与mock_L1
目录: 接口测试价值与体系常见的接口协议接口测试用例设计postman基础使用postman实战练习 1.接口测试价值与体系 接口测试概念 接口:不同的系统之间相互连接的部分,是一个传递数据的通道接口测试:检查数据的交换、传递和控制…...
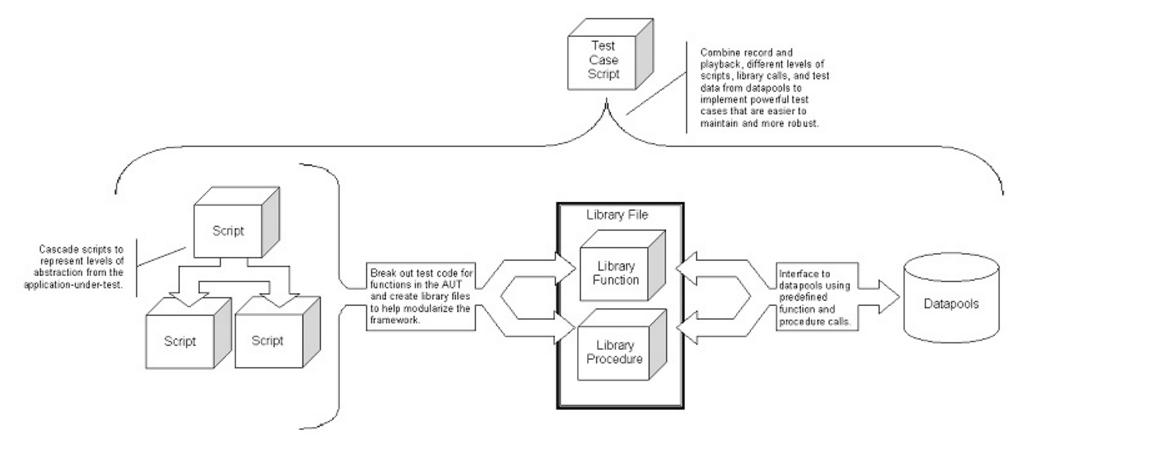
四种常用的自动化测试框架
一直想仔细研究框架,写个流水账似的测试程序不难,写个低维护成本的测试框架就很难了,所以研究多种测试框架还是很有必要的,知道孰优孰劣,才能在开始编写框架的时候打好基础,今天读到了KiKi Zhao的翻译文章&…...
Fuxploider:一款针对文件上传漏洞的安全检测与研究工具
Fuxploider:一款针对文件上传漏洞的安全检测与研究工具 1.概述2. 工具使用1.概述 Fuxploider是一款功能强大的开源渗透测试工具,该工具专门针对文件上传漏洞而设计,可以帮助广大研究人员以自动化的方式检测和利用目标站点文件上传表单中的安全问题 由于该工具基于Python 3…...

Unity 安装及运行MLAgents
1、下载ML-Agents 下载地址 GitHub - Unity-Technologies/ml-agents: The Unity Machine Learning Agents Toolkit (ML-Agents) is an open-source project that enables games and simulations to serve as environments for training intelligent agents using deep reinfo…...

LightDB-A 兼容oracle支持mod操作符
LightDB-A 兼容oracle支持mod操作符 LightDB-A 为了兼容oracle,从23.3版本开始支持mod操作符,其语义同 ‘%’ 操作符,使用案例如下: select 5 mod 2;?column? ----------1 (1 row)select 0 % 0; ERROR: division by zerosel…...

SpringMVC之自定义注解
目录 一、Java注解 1.1 注解简介 1.2 注解分类 1.3 JDK基本注解 1.4 JDK元注解 1.5 自定义注解 1.5.1 标记注解 1.5.2 元数据注解 1.6 如何自定义注解 二、自定义注解的基本案例 2.1 案例一(获取类、方法以及属性上的注解) 2.1.1 Ingerited的…...
QT:使用普通按钮、网格布局管理器、标签、行编辑器、水平布局管理器、垂直布局管理器做一个小项目
widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QPushButton> //普通按钮 #include <QGridLayout> //网格布局管理器 #include <QLabel> //标签 #include <QLineEdit> //行编辑器 #include <QHBoxLayo…...
【小沐学写作】程序员必备技能:在线协作文档汇总
文章目录 1、简介2、微软Office在线文档2.1 功能简介2.2 使用费用2.3 用户体验 3、石墨文档3.1 功能简介3.2 使用费用 4、腾讯文档4.1 功能简介4.2 使用费用 5、语雀5.1 功能简介5.2 使用费用 6、飞书6.1 功能简介6.2 使用费用 7、印象笔记7.1 功能简介7.2 使用费用 结语 1、简…...

「工具|数据接口」免费公开的REST API 如何借助github搭建自己的fake API接口
本文主要介绍日常开发、测试、教学或者分享中,可能遇到的模拟数据问题。分享免费开发的测试数据接口,以及如何利用github快速搭建定制化的接口数据,避免使用真实数据的风险以及自己现编数据的麻烦。 文章目录 一、场景说明二、免费公开的Fak…...

leetcode 18. 四数之和
给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] (若两个四元组元素一一对应,则认为两个四元组重复): 0 < a,…...

树上背包问题动态规划
目录 树状动态规划概述 示例 求解思路 树状动态规划概述 树状动态规划(Tree DP)是一种在树结构上进行动态规划的方法。在树状DP中,我们利用树的特殊结构性质,通过递归地向下更新子节点的状态,最终得到整个树的最…...

linux查看进程对应的线程(数)
首先,top或ps查看进程列表,确定要查看的进程pid,如下面40698 查看进程的线程情况 查看进程:top -p 40698 查看线程:top -p 40698 -d 3 -H 其中-d是刷新频率 可看到此进程共211个线程,运行中的是211个。…...

Python中的桌面应用开发库有哪些?
Python中有几个受欢迎的桌面应用开发库。以下是其中一些: Tkinter:这是Python的标准GUI库,它提供了构建简单的桌面应用程序的基本组件和功能。 PyQt:这是一个成熟的、功能强大的跨平台图形用户界面框架,它是Python绑定…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...
