当前位置： 首页 > news >正文

PDF怎么转图片？四种转换方法分享

news 2026/2/9 5:26:40

PDF文件是一种非常常见的文档格式，然而，有时候我们需要将PDF文件转换成图片格式。比如我们可能需要将PDF文件中的某些页面或图表转换成图片格式以便于编辑或分享。在这篇文章中，我们将介绍四种将PDF文件转换成图片的方法。

 

方法一：使用手机应用转换

经常习惯在手机上操作文档的小伙伴可以使用迅捷PDF转换器应用来进行转换。我们可以进入应用主页看到PDF转其他板块，选择PDF转图片功能，接着添加需要转换的文件导入进来即可进行转换。

 

方法二：使用在线转换工具

其实PDF转换器也有对应的桌面端，即使在电脑上来办公我们同样可以使用这款工具进行转换，在左侧的功能列表中选择文件转图片，将PDF文件添加进来点击开始转换按钮即可。

 

方法三：AdobeAcrobat

可能有很多小伙伴们不是太熟悉这个工具，其实这个工具也是个可以编辑PDF文件的工具，常用的PDF文档操作需求都可以使用这个工具来实现，只是工具本身的语言类型可能会增加操作上的难度，但是也不失为一个好用的方法。

 

方法四：直接使用截图功能

如果小伙伴只需要将PDF文件中的一部分内容转换成图片，则可以使用截图工具。我们常到的办公类型的工具或者部分电脑机型都有自带的截图功能，我们截取需要转换为图片的内容区域另存为图片格式即可。

 

以上是四种将PDF文件转换成图片的方法。小伙伴们可以自己的需求来选择其中适合自己的方法。希望这篇文章能够帮助到你。

相关文章：

PDF怎么转图片？四种转换方法分享

PDF文件是一种非常常见的文档格式，然而，有时候我们需要将PDF文件转换成图片格式。比如我们可能需要将PDF文件中的某些页面或图表转换成图片格式以便于编辑或分享。在这篇文章中，我们将介绍四种将PDF文件转换成图片的方法。 方法一&#xff1a…...

编程日记 2023/9/18 2:51:57

华为OD机试 - 压缩报文还原 - 正则表达式（Java 2023 B卷 100分）

目录 专栏导读一、题目描述二、输入描述三、输出描述四、解题思路五、Java算法源码六、效果展示1、输入2、输出3、说明 华为OD机试 2023B卷题库疯狂收录中，刷题点这里 专栏导读 本专栏收录于《华为OD机试（JAVA）真题（A卷B卷&#…...

编程日记 2023/9/18 2:47:53

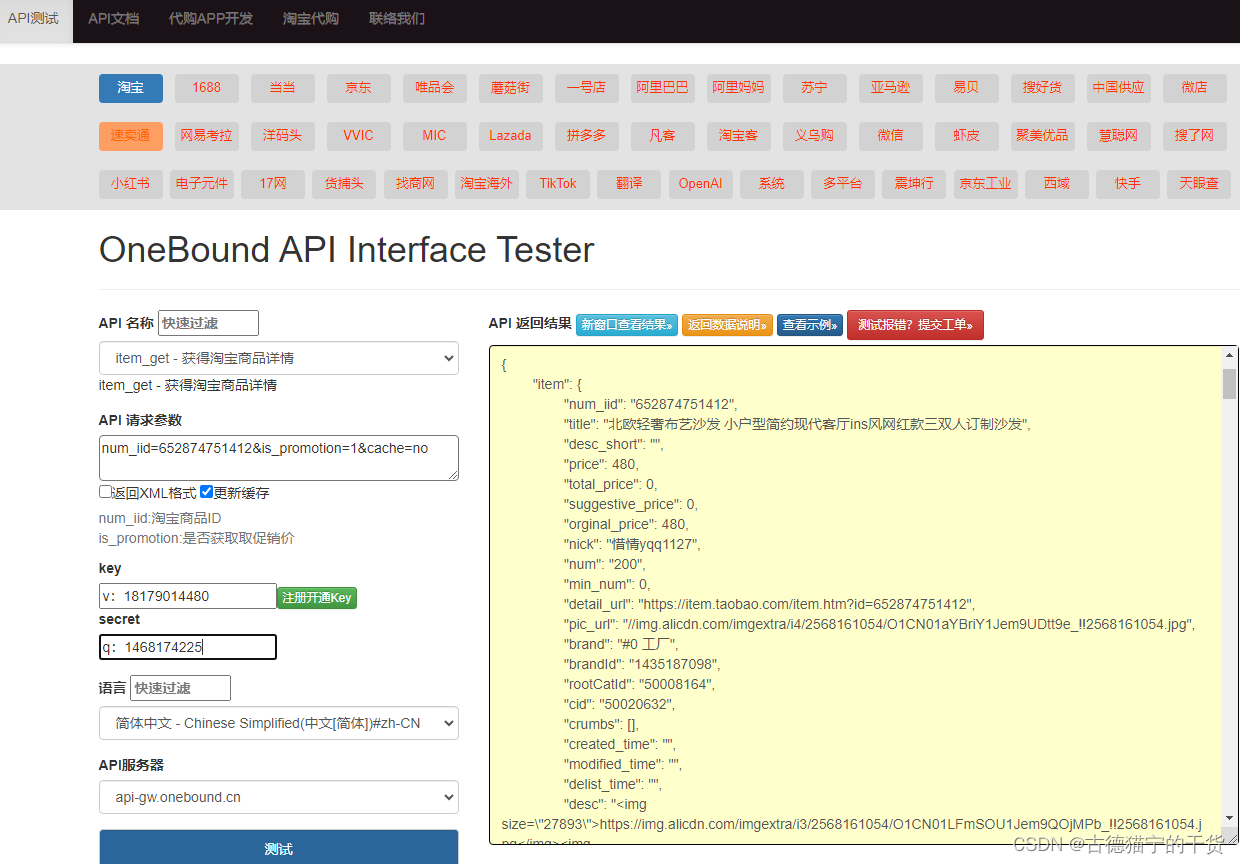
电商API的应用价值：淘宝1688京东API接口系列

API接口是一种软件应用程序，它充当两个不同软件应用程序之间的中介。它帮助不同的应用程序相互通信，共享数据，从而使用户能够完成不同的任务。API接口的用途非常广泛，下面是一些常见的用途： 数据共享：API接…...

编程日记 2023/9/18 2:45:51

day38 代码回想录 斐波那契数爬楼梯使用最小花费爬楼梯

大纲 ● 理论基础 ● 509. 斐波那契数 ● 70. 爬楼梯 ● 746. 使用最小花费爬楼梯 509. 斐波那契数 题目：509. 斐波那契数 // 斐波那契数列 // 动规 5部曲 // 1 dp[i]代表i处的斐波那契值 // 2 递归公式：dp[0] 0, dp[1]1, dp[i]dp[i-1]dp[i-2] // 3…...

编程日记 2023/9/18 2:44:50

Flink DataStream 体系

前言 本文隶属于专栏《大数据技术体系》，该专栏为笔者原创，引用请注明来源，不足和错误之处请在评论区帮忙指出，谢谢！ 本专栏目录结构和参考文献请见大数据技术体系 思维导图 正文 对 Flink 这种以流为核心的分布式计…...

编程日记 2023/9/18 2:43:49

Linux的调试工具 - gdb(超详细)

Linux的调试工具 - gdb 1. 背景2. 开始使用指令的使用都用下面这个C语言简单小代码来进行演示：1. list或l 行号：显示文件源代码，接着上次的位置往下列，每次列10行。2. list或l 函数名:列出某个函数的源代码。3. r或run: 运行程序。…...

编程日记 2023/9/18 2:41:46

已知平面内三点，求其平面的法向量

三点平面法向量 设三点坐标为A(x1,y1,z1),B(x2,y2,z2),C(x3,y3,z3) 向量AB(x2-x1,y2-y1,z2-z1),AC(x3-x1,y3-y1,z3-z1) AB、AC所在平面的法向量即ABAC(a,b,c),其中： a(y2-y1)(z3-z1)-(z2-z1)(y3-y1) b(z2-z1)(x3-x1)-(z3-z1)(x2-x1) c(x2-x1)(y3-y1)-(x3-x1)(y2-y1)…...

编程日记 2023/9/18 2:40:44

HTML

HTML 1.HTML结构 1.1认识HTML HTML是超文本标记语言&#xff0c;电脑上看到的所有网站都是html实现的 HTML代码是“标签”构成的&#xff0c;简单来说&#xff0c;html就是一堆标签的组合 形如 <body>hello</body>标签名 (body) 放到 < > 中 大部分标签成…...

编程日记 2023/9/18 2:39:43

Java手写最大子数组和算法（如Kadane算法）和最大子数组和算法（如Kadane算法）应用拓展案例

Java手写最大子数组和算法&#xff08;如Kadane算法&#xff09;和最大子数组和算法&#xff08;如Kadane算法&#xff09;应用拓展案例 1. 算法思维导图 以下是使用mermaid代码表示的Kadane算法的实现原理&#xff1a; #mermaid-svg-rI7hVAVsP1qtjZK7 {font-family:"tr…...

编程日记 2023/9/18 2:35:38

掌握NVM、NRM和NPM：Node.js开发的利器

**掌握NVM、NRM和NPM&#xff1a;Node.js开发的利器** 背景介绍&#xff1a;如何使用NVM&#xff1a;在Windows上安装NVM&#xff1a;在macOS上安装NVM&#xff1a;配置NVM&#xff1a;常用NVM命令&#xff1a; 如何使用NRM&#xff1a;安装NRM&#xff1a;配置全局NRM&#xf…...

编程日记 2023/9/18 2:33:36

Nacos 2.2.3 部署到linux

到https://github.com/alibaba/nacos/releases 下载编译后压缩包&#xff0c;如nacos-server-2.2.3.tar.gz这种&#xff0c;里面包含有nacos的jar包&#xff0c;不然启动不了 1.新建并初始化数据库 创建nacos数据库&#xff0c;执行mysql-schema.sql文件&#xff0c;这个文件…...

编程日记 2023/9/18 2:27:31

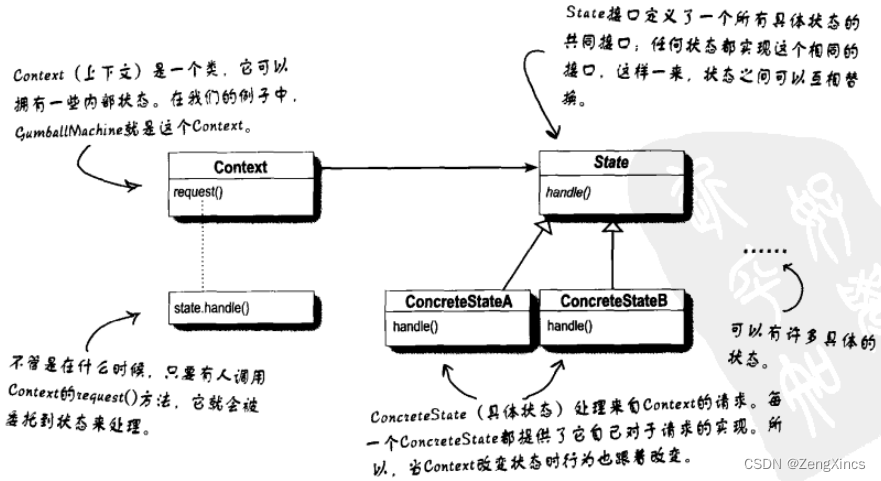
设计模式之十：状态模式

状态模式通过改变对象内部的状态来帮助对象控制自己的行为。 这是一张状态图&#xff0c;其中每个圆圈都是一个状态。 最简单&#xff0c;第一反应的实现就是使用一个变量来控制状态值&#xff0c;并在方法内书写条件代码来处理不同情况。 package headfirst.designpatterns.…...

编程日记 2023/9/18 2:25:29

Python 的运算符和语句（条件、循环、异常）基本使用指南

运算符的分类 算数运算符赋值运算符复合赋值运算符比较运算符逻辑运算符 算数运算符 运算符描述实例加1 1 输出结果为 2-减1 - 1 输出结果为 0*乘2 * 2 输出结果为 4/除10 / 2 输出结果为 5//整除9 // 4 输出结果为 2%取余9 % 4 输出结果为 1**指数2 ** 4 输出结果为 16&…...

编程日记 2023/9/18 2:24:28

文心一言 VS 讯飞星火 VS chatgpt （94）-- 算法导论9.2 3题

三、用go语言&#xff0c;给出 RANDOMIZED-SELECT的一个基于循环的版本。 文心一言&#xff1a; 在循环中实现 RANDOMIZED-SELECT 的一个版本可以如下所示。这个版本使用 Go 语言编写&#xff0c;利用随机化来选择一个元素&#xff0c;并在循环中不断地调整选择的元素&#x…...

编程日记 2023/9/18 2:22:26

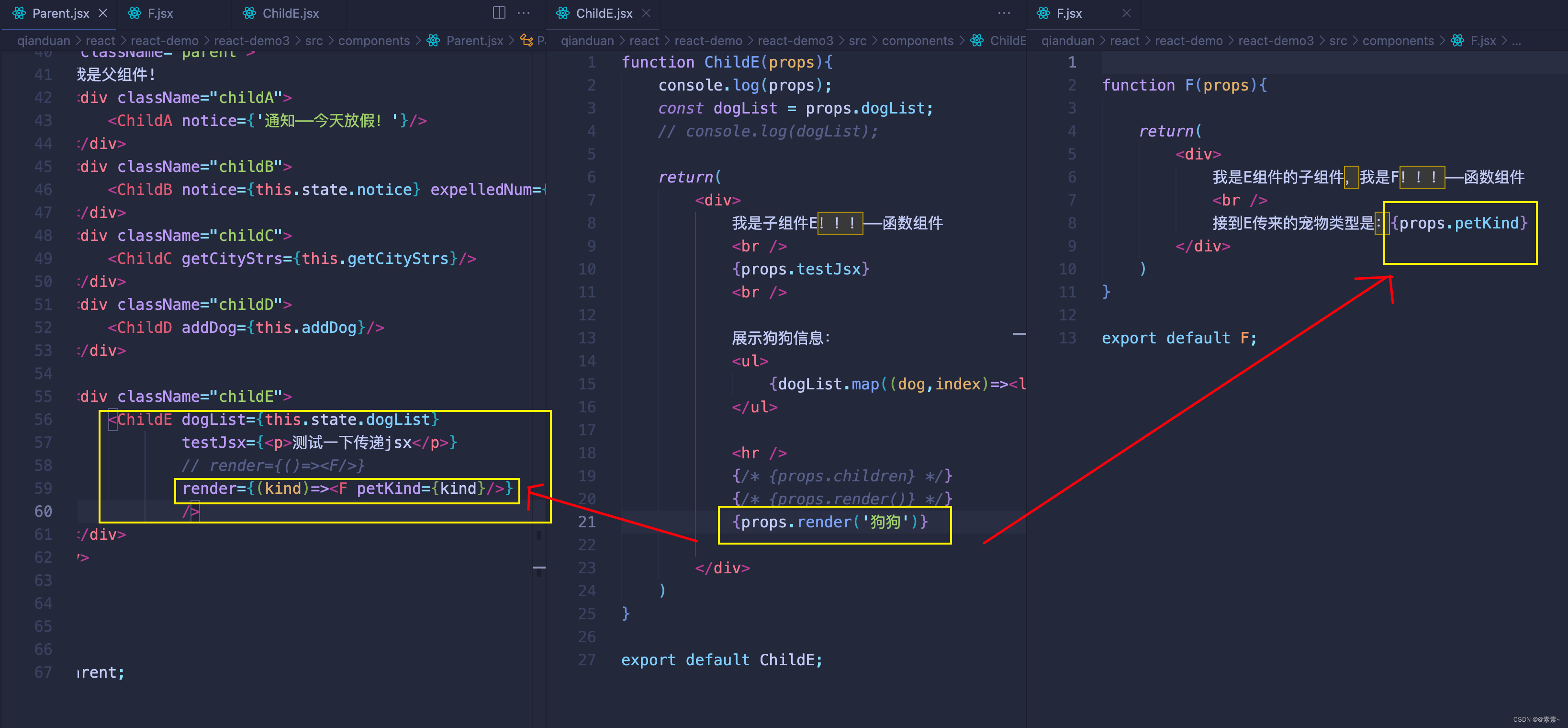
React中组件通信01——props

React中组件通信01——props 1. 父传子——props1.1 简单例子——props1.2 props 可以传递任何数据1.2.1 传递数字、对象等1.2.2 传递函数1.2.3 传递模版jsx 2. 子传父 子传子——props2.1 父传子——传递函数2.2 子传父——通过父传子的函数实现2.3 优化 子传子&#xff08;…...

编程日记 2023/9/18 2:21:26

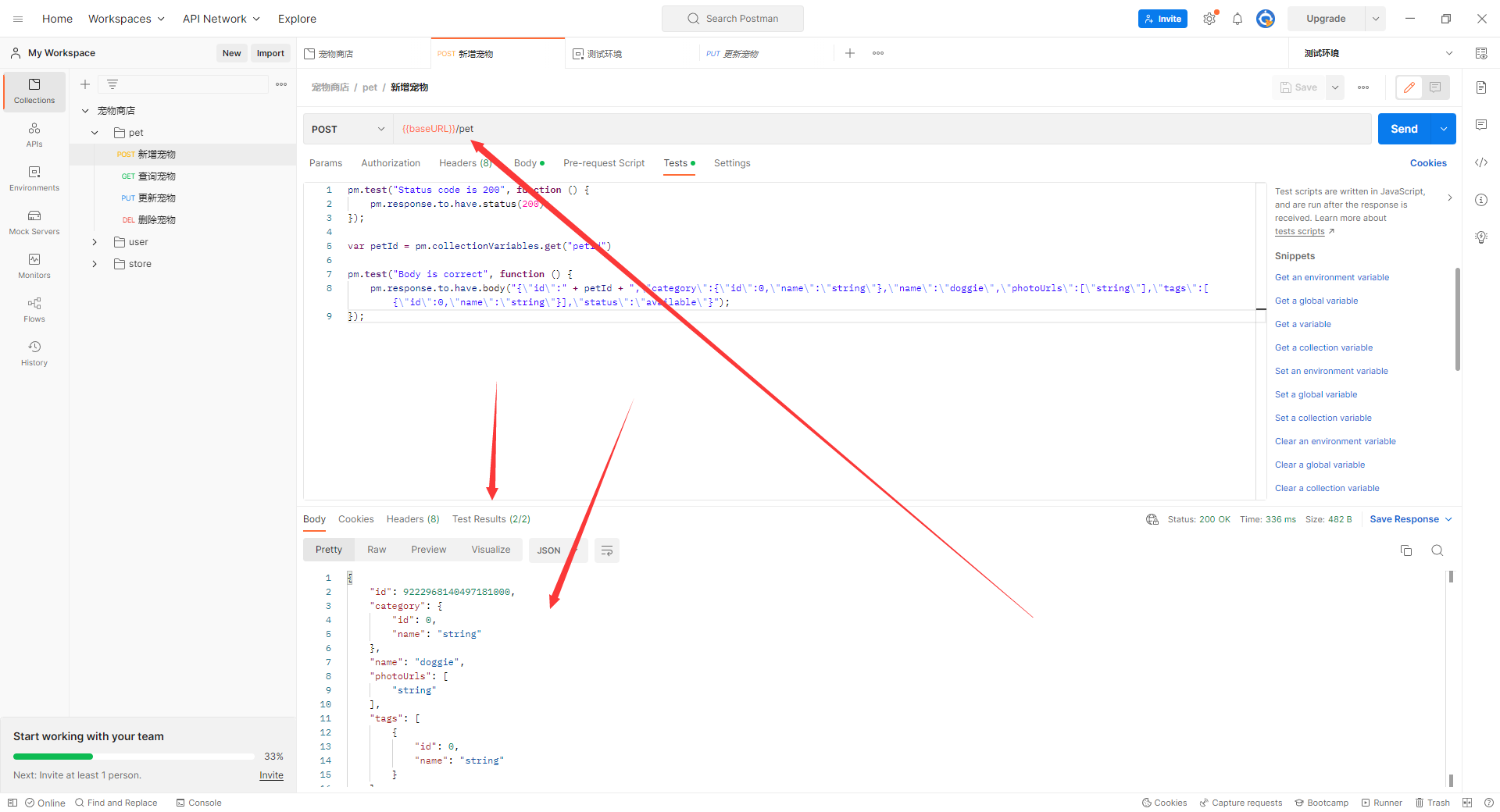
接口测试——接口协议抓包分析与mock_L1

目录&#xff1a; 接口测试价值与体系常见的接口协议接口测试用例设计postman基础使用postman实战练习 1.接口测试价值与体系 接口测试概念 接口&#xff1a;不同的系统之间相互连接的部分&#xff0c;是一个传递数据的通道接口测试&#xff1a;检查数据的交换、传递和控制…...

编程日记 2023/9/18 2:19:24

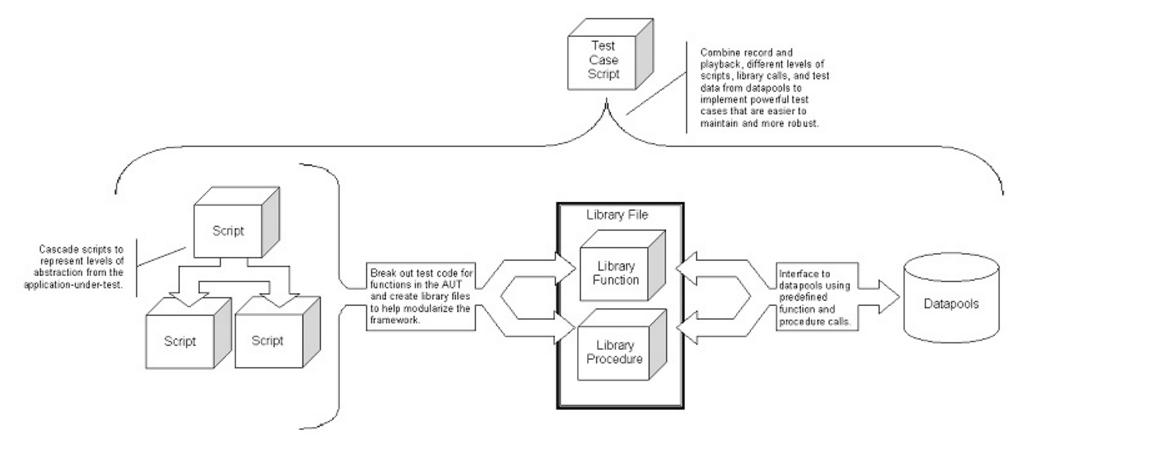
四种常用的自动化测试框架

一直想仔细研究框架&#xff0c;写个流水账似的测试程序不难&#xff0c;写个低维护成本的测试框架就很难了&#xff0c;所以研究多种测试框架还是很有必要的&#xff0c;知道孰优孰劣&#xff0c;才能在开始编写框架的时候打好基础&#xff0c;今天读到了KiKi Zhao的翻译文章&…...

编程日记 2023/9/18 2:18:23

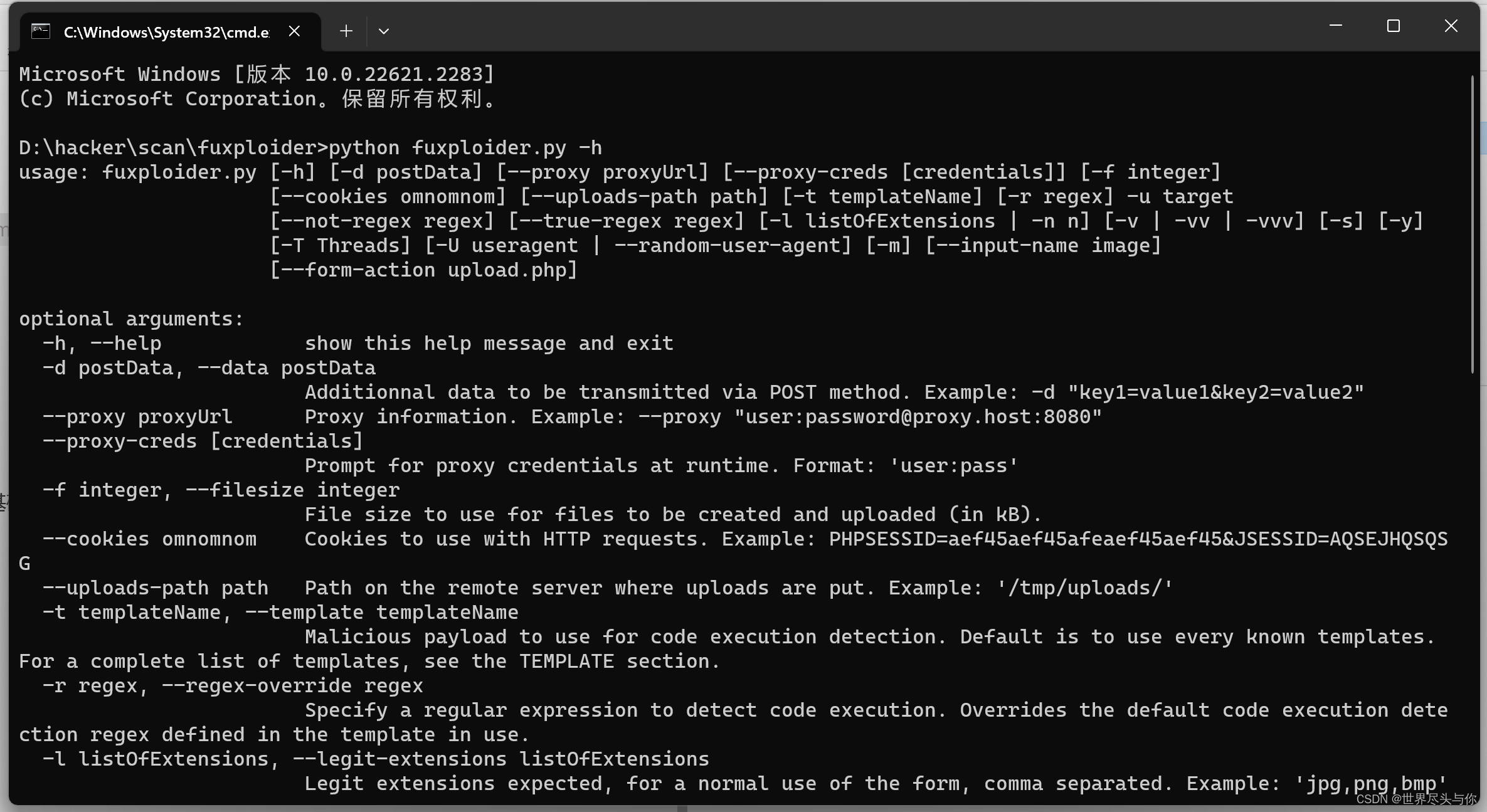
Fuxploider：一款针对文件上传漏洞的安全检测与研究工具

Fuxploider：一款针对文件上传漏洞的安全检测与研究工具 1.概述2. 工具使用1.概述 Fuxploider是一款功能强大的开源渗透测试工具，该工具专门针对文件上传漏洞而设计，可以帮助广大研究人员以自动化的方式检测和利用目标站点文件上传表单中的安全问题 由于该工具基于Python 3…...

编程日记 2023/9/18 2:17:22

Unity 安装及运行MLAgents

1、下载ML-Agents 下载地址 GitHub - Unity-Technologies/ml-agents: The Unity Machine Learning Agents Toolkit (ML-Agents) is an open-source project that enables games and simulations to serve as environments for training intelligent agents using deep reinfo…...

编程日记 2023/9/18 2:11:17

LightDB-A 兼容oracle支持mod操作符

LightDB-A 兼容oracle支持mod操作符 LightDB-A 为了兼容oracle&#xff0c;从23.3版本开始支持mod操作符&#xff0c;其语义同 ‘%’ 操作符&#xff0c;使用案例如下&#xff1a; select 5 mod 2;?column? ----------1 (1 row)select 0 % 0; ERROR: division by zerosel…...

编程日记 2023/9/18 2:09:15

Java 语言特性(面试系列2)

一、SQL 基础 1. 复杂查询 &#xff08;1&#xff09;连接查询&#xff08;JOIN&#xff09; 内连接&#xff08;INNER JOIN&#xff09;&#xff1a;返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

编程新知 2025/10/24 14:20:29

1688商品列表API与其他数据源的对接思路

将1688商品列表API与其他数据源对接时&#xff0c;需结合业务场景设计数据流转链路&#xff0c;重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点&#xff1a; 一、核心对接场景与目标 商品数据同步 场景&#xff1a;将1688商品信息…...

编程新知 2025/11/30 16:55:32

Linux简单的操作

ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

编程新知 2026/1/20 14:36:39

MVC 数据库

MVC 数据库 引言 在软件开发领域，Model-View-Controller（MVC）是一种流行的软件架构模式，它将应用程序分为三个核心组件：模型（Model）、视图（View）和控制器（Controller）。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系，以…...

编程新知 2025/10/30 4:58:11

HBuilderX安装（uni-app和小程序开发）

下载HBuilderX 访问官方网站&#xff1a;https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本&#xff1a; Windows版&#xff08;推荐下载标准版&#xff09; Windows系统安装步骤 运行安装程序&#xff1a; 双击下载的.exe安装文件 如果出现安全提示&…...

编程新知 2026/1/31 12:52:04

DBAPI如何优雅的获取单条数据

API如何优雅的获取单条数据 案例一 对于查询类API&#xff0c;查询的是单条数据&#xff0c;比如根据主键ID查询用户信息&#xff0c;sql如下&#xff1a; select id, name, age from user where id #{id}API默认返回的数据格式是多条的&#xff0c;如下&#xff1a; {&qu…...

编程新知 2026/2/2 22:06:13

Web 架构之 CDN 加速原理与落地实践

文章目录 一、思维导图二、正文内容&#xff08;一&#xff09;CDN 基础概念1. 定义2. 组成部分 &#xff08;二&#xff09;CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 &#xff08;三&#xff09;CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 &#xf…...

编程新知 2025/9/13 16:17:01

iOS性能调优实战：借助克魔(KeyMob)与常用工具深度洞察App瓶颈

在日常iOS开发过程中&#xff0c;性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期&#xff0c;开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发&#xff0c;但背后往往隐藏着系统资源调度不当…...

编程新知 2025/9/24 12:50:07

使用Spring AI和MCP协议构建图片搜索服务

目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式&#xff08;本地调用&#xff09; SSE模式&#xff08;远程调用&#xff09; 4. 注册工具提…...

编程新知 2026/1/25 14:31:47

08. C#入门系列【类的基本概念】：开启编程世界的奇妙冒险

C#入门系列【类的基本概念】&#xff1a;开启编程世界的奇妙冒险 嘿&#xff0c;各位编程小白探险家&#xff01;欢迎来到 C# 的奇幻大陆&#xff01;今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类&#xff01;别害怕&#xff0c;跟着我&#xff0c;保准让你轻松搞…...

编程新知 2025/10/31 20:37:10