大数据算法
1. TOP K 算法
有10个⽂件,每个⽂件1G,每个⽂件的每⼀⾏存放的都是⽤户的 query,每个⽂件的 query 都可能重复。要求你按照 query 的频度排序。
方法1:
顺序读取10个⽂件,按照 hash(query)%10 的结果将 query 写⼊到另外 10 个⽂件(记为)中。这样新⽣成的⽂件每个的⼤⼩⼤约也 1G(假设 hash 函数是随机的)。找⼀台内存在 2G 左右的机器,依次对⽤hash_map(query, query_count)来统计每个 query 出现的次数。利⽤快速/堆/归并排序按照出现次数进⾏排序。将排序好的 query 和对应的 query_cout 输出到⽂件中。这样得到了 10 个排好序的⽂件(记为)。对这 10 个⽂件进⾏归并排序(内排序与外排序相结合)。
方法2:
与⽅案 1 类似,但在做完 hash,分成多个⽂件后,可以交给多个⽂件来处理,采⽤分布式的架构来处理(⽐如 MapReduce),最后再进⾏合并。
2. 不重复的数据
在 2.5 亿个整数中找出不重复的整数,注,内存不⾜以容纳这 2.5 亿个整数。
解答:
1)⽅案 1:采⽤ 2-Bitmap(每个数分配 2bit,00 表示不存在,01 表示出现⼀次,10 表示多次,11 ⽆意义)进⾏,共需内存 2^32 * 2bit=1 GB 内存,还可以接受。然后扫描这 2.5 亿个整数,查看 Bitmap 中相对应位,如果是 00 变 01,01 变 10,10 保持不变。所描完事后,查看 bitmap,把对应位是 01 的整数输出即可。
2)⽅案 2:也可采⽤与第 1 题类似的⽅法,进⾏划分⼩⽂件的⽅法。然后在⼩⽂件中找出不重复的整数,并排序。然后再进⾏归并,注意去除重复的元素。
3. 判断数据是否存在
给 40 亿个不重复的 unsigned int 的整数,没排过序的,然后再给⼀个数,如何快速判断这个数是否在那 40 亿个数当中?
1)⽅案 1:oo,申请 512M 的内存,⼀个 bit 位代表⼀个 unsigned int 值。读⼊ 40 亿个数,设置相应的 bit 位,读⼊要查询的数,查看相应 bit 位是否为 1,为 1 表示存在,为 0 表示不存在。
4. 重复最多的数据
有⼀千万条短信,有重复,以⽂本⽂件的形式保存,⼀⾏⼀条,有重复。请⽤5分钟时间,找出重复出现最多的前 10 条。
解答:
1)分析: 常规⽅法是先排序,在遍历⼀次,找出重复最多的前 10 条。但是排序的算法复杂度最低为 nlgn。
2)可以设计⼀个 hash_table, hash_map<string, int>,依次读取⼀千万条短信,加载到 hash_table 表 中,并且统计重复的次数,与此同时维护⼀张最多 10 条的短信表。 这样遍历⼀次就能找出最多的前 10 条,算法复 杂度为 O(n)。
相关文章:

大数据算法
1. TOP K 算法 有10个⽂件,每个⽂件1G,每个⽂件的每⼀⾏存放的都是⽤户的 query,每个⽂件的 query 都可能重复。要求你按照 query 的频度排序。 方法1: 顺序读取10个⽂件,按照 hash(query)%10 的结果将 query 写⼊到…...

非暴力沟通读书笔记
浅读《非暴力沟通》,本书对于沟通的方式总结成了一个方法论,从13个章节去概述非暴力沟通的方法和重点。其中最重要的是非暴力沟通四要素,观察、感受、需要、请求。同时在沟通中注意观察,投入爱,重视倾听的力量…...
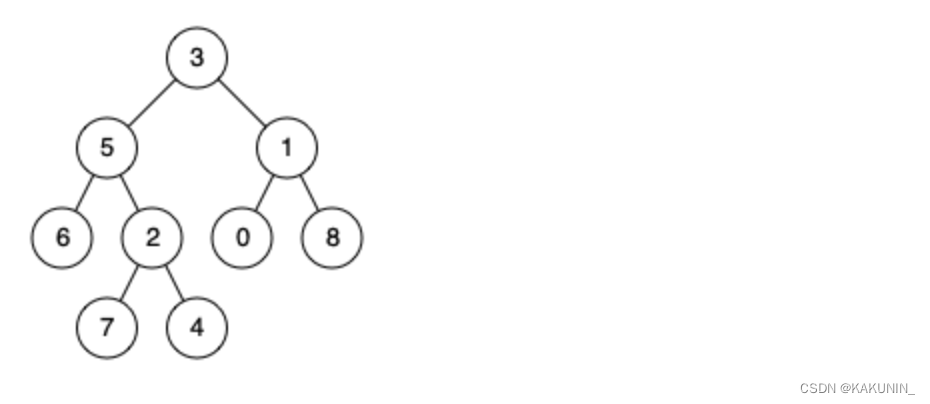
代码随想录【Day21】| 530. 二叉搜索树的最小绝对差、501. 二叉搜索树中的众数、236. 二叉树的最近公共祖先
530. 二叉搜索树的最小绝对差 题目链接 题目描述: 给你一棵所有节点为非负值的二叉搜索树,请你计算树中任意两节点的差的绝对值的最小值。 示例: 提示:树中至少有 2 个节点。 难点: 解答错误!仅考虑了…...
注意啦,面试通过后,别忘了教师资格证认定
所有要「教师资格证认定」教程的宝子们看过来面试合格的小伙伴都可以进行认定工作 . 认定时间 查询各省份认定公告,确定认定时间范围。以下是公告汇总网址(https://www.jszg.edu.cn/portal/qualification_cert/dynamics?id21691) 认定次数 每…...
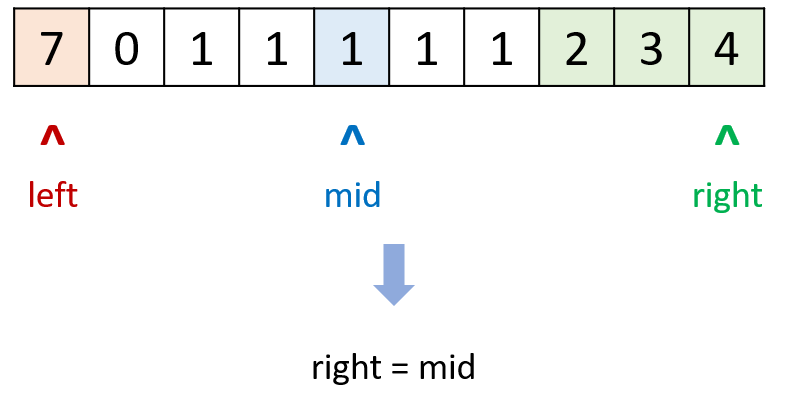
【LeetCode】No.154. 寻找旋转排序数组中的最小值 II -- Java Version
题目链接:https://leetcode.cn/problems/find-minimum-in-rotated-sorted-array-ii/ 1. 题目介绍(154. 寻找旋转排序数组中的最小值 II) 已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后࿰…...

RestTemplate远程调用
我们现在项目中使用的RPC远程调用技术是Dubbo实际上除了Dubbo技术之外,还有很多远程调用的方法它们有些调用的思想都和Dubbo完全不同Dubbo是SpringCloudAlibaba提供的功能强大的RPC框架但是Dubbo功能也有限制,如果我们想调用的方法不是我们当前项目的组件或功能,甚至想调用的方…...

registerForActivityResult使用
目录 针对 activity 结果注册回调 启动 activity 以获取其结果 在单独的类中接收 activity 结果 测试 创建自定义协定 registerForActivityResult()是startActivityForResult()的替代,简化了数据回调的写法 启动另一个 activity&#x…...

工作中,python真的有用吗?
普通上班族学Python有用吗? 那么,我也在这里提出一个问题:Python究竟适不适合办公人士来学习,以及学了之后究竟能不能给我的工作来带质一般的飞跃? 以我的亲身经历为例,我可以很负责的告诉大家,…...
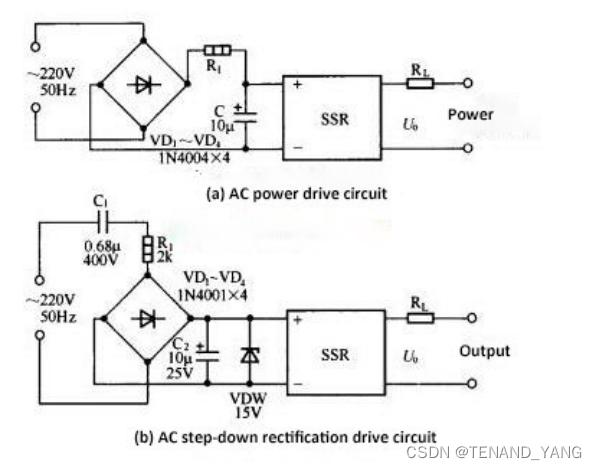
固态继电器控制电路
固态继电器控制电路 固态继电器(SSR)的种类和型号很多,因此其输入控制方法和控制电路也相应众多。固态继电器(SSR)的共同特点在于驱动电流或驱动电压小,即只需输入一个小信号即可控制SSR的开关。 如果需要…...
数仓、数据湖、湖仓一体、数据网格的探索与研究
第一代:数据仓库 定义 为解决数据库面对数据分析的不足,孕育出新一类产品数据仓库。数据仓库(Data Warehouse)是一个面向主题的、集成的、相对稳定的、反映历史变化的数据集合,用于支持管理决策和信息的全局共享。 数…...

设计模式系列 - 备忘录模式
介绍&定义 备忘录模式,也叫快照(Snapshot)模式,英文翻译是 Memento Design Pattern。在 GoF 的《设计模式》一书中,备忘录模式是这么定义的: Captures and externalizes an object’s internal state…...

详细介绍React生命周期和diffing算法
事件处理 1.通过onXxx属性指定事件处理函数(注意大小写) React使用的是自定义(合成)事件, 而不是使用的原生DOM事件 —— 为了更好的兼容性;React中的事件是通过事件委托方式处理的(委托给组件最外层的元素) ——为了的高效。 2.通过event.target得到发生事件的DOM…...

面向对象的特点
1、什么是对象对象的含义是指具体的某一个事物,即在现实生活中能够看得见摸得着的事物。在面向对象程序设计中,对象所指的是计算机系统中的某一个成分。在面向对象程序设计中,对象包含两个含义,其中一个是数据,另外一个…...
智慧校园平台源码 智慧教务 智慧电子班牌系统
系统介绍 智慧校园系统是通过信息化手段,实现对校园内各类资源的有效集成 整合和优化,实现资源的有效配置和充分利用,将校务管理过程的优化协调。为校园提供数字化教学、数字化学习、数字化科研和数字化管理。 致力于为家长和教师提供一个全方位、多层…...
])
Vue篇.03-组合式API [setup()]
单文件组件(1)<script setup><script setup> 是在单文件组件 (SFC) 中使用组合式 API 的编译时语法糖。当同时使用 SFC 与组合式 API 时该语法是默认推荐启用该语法,需要在 <script> 代码块上添加 setup attribute, 里面的代码会被编译成组件 s…...
QHashIterator-官翻
QHashIterator Class template <typename Key, typename T> class QHashIterator QHashIterator 类为 QHash 和 QMultiHash 提供 Java 风格的常量迭代器。更多内容… 头文件:#include qmake:QT core 所有成员列表,包括继承的成员废弃的成员 公共成员函数…...

[qiankun]-部署后线上问题
[qiankun]-部署后线上问题微服务加载问题-现象1现象描述问题分析解决方案微服务加载问题-现象2现象描述问题分析微服务加载问题-现象3现象描述分析解决方案属于项目打包后,部署到服务器上,所遇到的部分问题 微服务加载问题-现象1 现象描述 项目部署实…...

位图数组 布隆过滤器
文章目录位图数组获取索引获取索引状态设置索引状态布隆过滤器特点大致原理位图数组 一个int类型的整数用4字节,也就是32个bit位来表示,将整数类型的数组转换成位图数组,那么存储长度将变为原来的32倍 arr[0] 表示0-31 arr[1] 表示32-63 //...获取索引…...
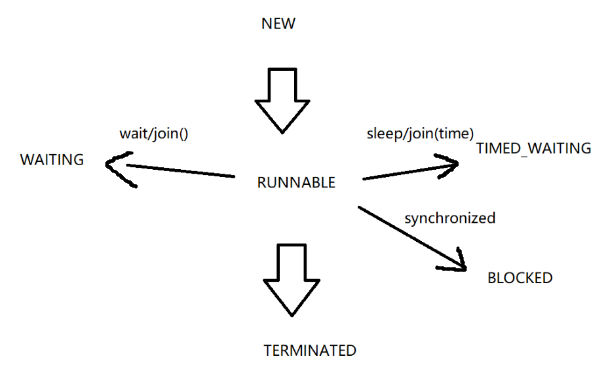
多线程Thread常用方法和状态
Thread类 及常见方法 1、常见构造方法 方法说明Thread()创建线程对象Thread(Runnable target)使用 Runnable 对象创建线程对象Thread(String name)创建线程对象,并命名Thread(Runnable target, String name)使用 Runnable 对象创建线程对象,并命名Thre…...
Codeforces Round #836 (Div. 2)
A SSeeeeiinngg DDoouubbllee 题意:告诉你一个字符串。若该串上每一位上的字母都可以出现两次,求回文串 思路:正向再反向输出s即可 #include <bits/stdc.h> #define lowbit(x) x&(-x) #define ios cin.sync_with_stdio(false)…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...

rm视觉学习1-自瞄部分
首先先感谢中南大学的开源,提供了很全面的思路,减少了很多基础性的开发研究 我看的阅读的是中南大学FYT战队开源视觉代码 链接:https://github.com/CSU-FYT-Vision/FYT2024_vision.git 1.框架: 代码框架结构:readme有…...
