二叉树的概念、存储及遍历
一、二叉树的概念
1、二叉树的定义
二叉树( binary tree)是 n 个结点的有限集合,该集合或为空集(空二叉树),或由一个根结点与两棵互不相交的,称为根结点的左子树、右子树的二叉树构成。
二叉树的特点是:
(1)每个结点最多有两棵子树,故二叉树中不存在度大于 2 的结点。
(2)二叉树是有序的,其次序不能任意颠倒,即使树中的某个结点只有一棵子树,也要区分它是左子树还是右子树。
二叉树具有以下 5 种基本形态:
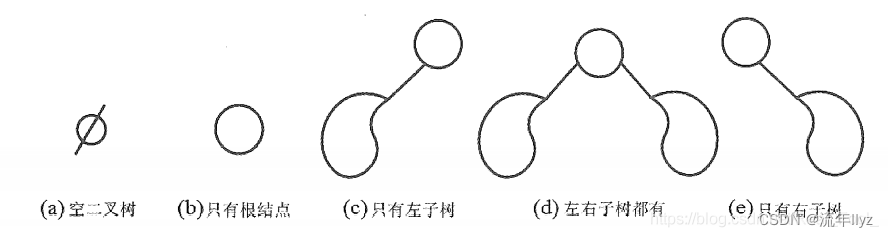 1、
1、
2、特殊的二叉树
在实际应用中,常会用到以下几种特殊的二叉树。
1.斜树
所有的结点都只有左子树的二叉树称为左斜树,所有的结点都只有右子树的二叉树称为右斜树,在斜树中,每层只有一个结点,因此斜树的结点个数与其深度相同.
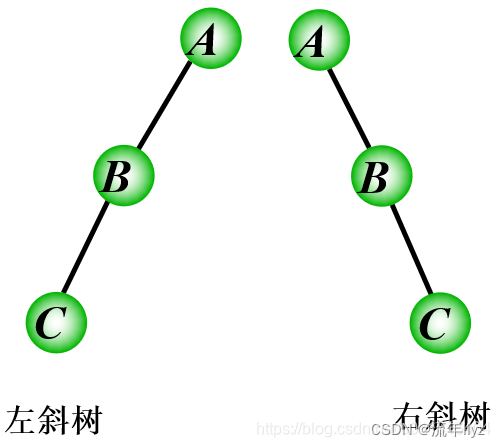
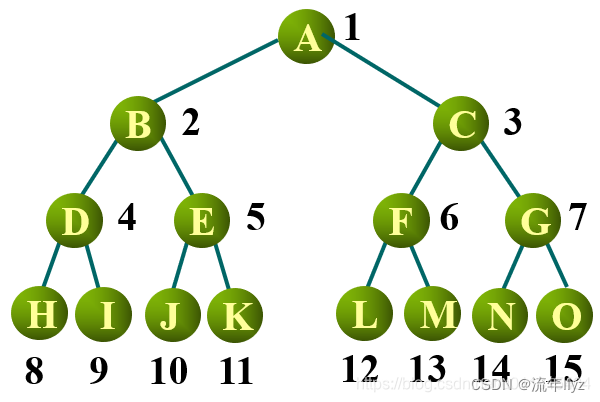
2.满二叉树
在一棵二叉树中,若所有的分支结点都存在左子树和右子树,且所有的叶子都在同一层上,则称为满二叉树。
其特点是:
- 叶子只能出现在最下一层
- 只有度为 0、度为 2 的结点
由于满二叉树的特性可知:满二叉树在同样深度的二叉树中结点个数、叶结点个数最多。
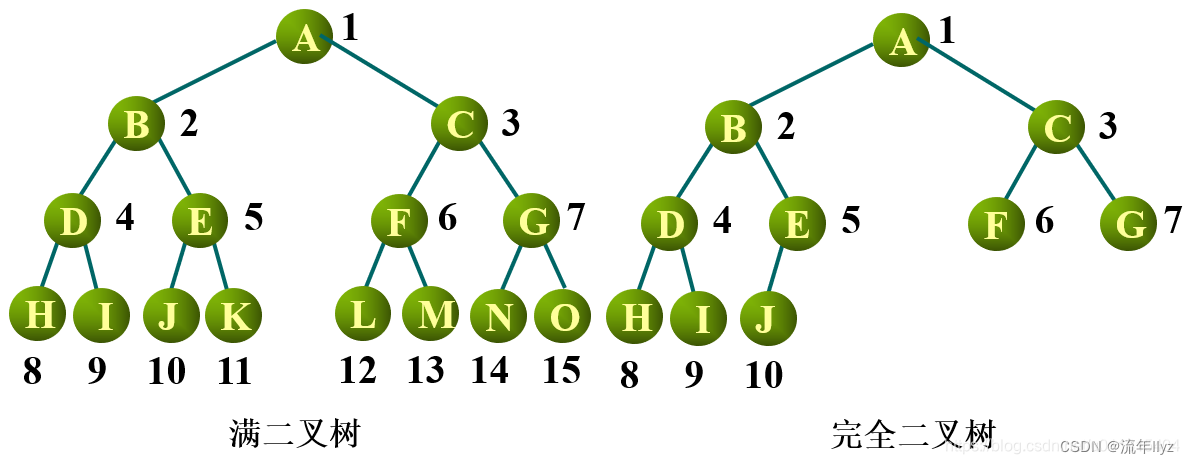
3.完全二叉树
对一棵具 n 个结点的二叉树按层序编号,若编号为 i 的结点与同样深度的满二叉树中编号 i 的结点在二叉树中的位置完全相同,则称为完全二叉树,那么显然有:满二叉树是完全二叉树
其特点是:
(1)若i ≤ n / 2, 则结点i为分支结点,否则为叶子结点。
(2)叶子结点只可能在层次最大的两层上出现。对于最大层次中的叶子结点,都依次排列在该层最左边的位置上。
(3)若有度为1的结点,则只可能有一个,且该结点只有左孩子而无右孩子(重要特征)。
(4)按层序编号后,一旦出现某结点(编号为i)为叶子结点或只有左孩子,则编号大于i 的结点均为叶子结点。
(5)若n为奇数,则每个分支结点都有左孩子和右孩子;若n为偶数,则编号最大的分支结点(编号为n / 2 )只有左孩子,没有右孩子,其余分支结点左、右孩子都有。
简单来说,在满二叉树中,从最后一个结点开始,连续去掉任意个的结点,即是一棵完全二叉树
3、二叉树的性质
1.非空二叉树的第 i 层上行最多有 个结点
2.在一棵深度为 k 的二叉树中,最多有 个结点,最少有 k 个结点
推论:深度为 k 且具 个结点的二叉树一定是满二叉树,但深度为 k 具有 k 个结点的二叉树不一定是斜树
3.任意一棵树,若结点数量为n ,则边的数量为n − 1 。
4.在一棵二叉树中,若叶结点个数为 ,度为 2 结点个数为
,那么有:
5.具有 n 个结点的完全二叉树的深度为 ,
6.对完全二叉树按从上到下、从左到右的顺序依次编号1 , 2,...,n,则有以下关系:
(1)若 i=1,则:结点 i 为根节点;若 i>1,则:结点 i 的父结点编号为 i / 2,即当i 为偶数时, 它是双亲的左孩子;当i为奇数时,它是双亲的右孩子。
(2)若2 i ≤ n 时,结点i 的左孩子编号为2 i , 否则无左孩子。
(3)若2 i + 1 ≤ n 时,结点i 的右孩子编号为2 i + 1 ,否则无右孩子。
(4)结点i 所在层次(深度)为
4、二叉树的存储结构
1、顺序存储结构
二叉树的顺序存储结构是用一维数组存储二叉树中的结点,并用结点的存储位置表示结点间的逻辑关系(父子关系)
由于二叉树本身不具有顺序关系,因此二叉树的顺序存储结构要解决的关键问题是如何利用数组下标来反映结点间的逻辑关系。
由于完全二叉树中结点的层序编号可以唯一反映结点间的逻辑关系,因此对于一般的二叉树,可以添加一些不存在的空结点,使其成为一棵完全二叉树,再利用一维数组存储。
具体步骤为:
1、根节点编号为 1
2、若某结点 i 有左孩子,则其左孩子编号为 2i
3、若某结点 i 有右孩子,则其右孩子编号为 2i+1

缺陷:顺序存储会造成存储空间的浪费,最坏的情况是右斜树,一棵深度为 k 的右斜树,却要分配 个存储空间。
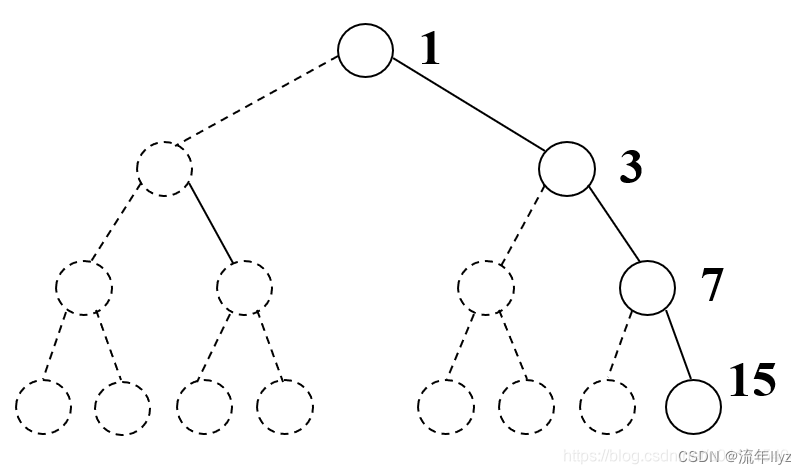
因此,二叉树的顺序存储结构一般仅用于存储完全二叉树。
2、链式存储结构
既然顺序存储适用性不强,我们就要考虑链式存储结构。二叉树每个结点最多有两个孩子,所以为它设计一个数据域和两个指针域是比较自然的想法,我们称这样的链表叫做二叉链表。
| lchild | data | rchild |
其中data是数据域,lchild 和rchild都是指针域,分别存放指向左孩子和右孩子的指针。
以下是我们的二叉链表的结点结构定义代码。
/*二叉树的二叉链表结点构造定义*/
/*结点结构*/
struct BiTNode{TElemType data; //结点数据BiTNode *lchild, *rchild; //左右孩子指针
} BiTNode, *BiTree; //根结点
容易验证,在含有n 个结点的二叉链表中,含有n + 1 个空链域。
二、遍历二叉树
二叉树的遍历是指从根结点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次且仅被访问一次。
1、先序遍历
先序遍历(PreOrder) 的操作过程如下:若二叉树为空,则什么也不做,否则,
1)访问根结点;
2)先序遍历左子树;
3)先序遍历右子树。
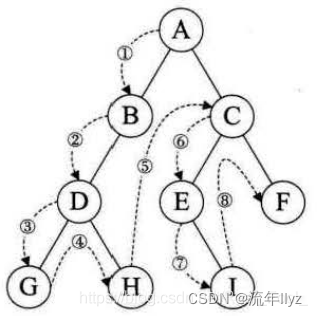
2、中序遍历
中序遍历( InOrder)的操作过程如下:若二叉树为空,则什么也不做,否则,
1)中序遍历左子树;
2)访问根结点;
3)中序遍历右子树。
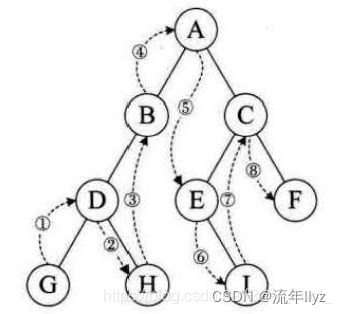
3、后序遍历
后序遍历( InOrder)的操作过程如下:若二叉树为空,则什么也不做,否则,
1)中序遍历左子树;
2)中序遍历右子树。
3)访问根结点;
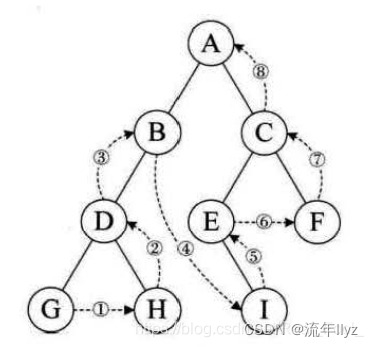
三种遍历算法中,递归遍历左、右子树的顺序都是固定的,只是访问根结点的顺序不同。不管采用哪种遍历算法,每个结点都访问一次且仅访问一次,故时间复杂度都是O(n)。在递归遍历中,递归工作栈的栈深恰好为树的深度,所以在最坏情况下,二叉树是有n个结点且深度为n的单支树,遍历算法的空间复杂度为O(n)。
相关文章:

二叉树的概念、存储及遍历
一、二叉树的概念 1、二叉树的定义 二叉树( binary tree)是 n 个结点的有限集合,该集合或为空集(空二叉树),或由一个根结点与两棵互不相交的,称为根结点的左子树、右子树的二叉树构成。 二叉树的…...
【面试题】智力题
文章目录 腾讯1000瓶毒药里面只有1瓶是有毒的,问需要多少只老鼠才能在24小时后试出那瓶有毒。有两根不规则的绳子,两根绳子从头烧到尾均需要一个小时,现在有一个45分钟的比赛,裁判员忘记带计时器,你能否通过烧绳子的方…...
【SpringBoot集成Redis + Session持久化存储到Redis】
目录 SpringBoot集成Redis 1.添加 redis 依赖 2.配置 redis 3.手动操作 redis Session持久化存储到Redis 1.添加依赖 2.修改redis配置 3.存储和读取String类型的代码 4.存储和读取对象类型的代码 5.序列化细节 SpringBoot集成Redis 1.添加 redis 依赖 …...

day49:QT day2,信号与槽、对话框
一、完善登录框 点击登录按钮后,判断账号(admin)和密码(123456)是否一致,如果匹配失败,则弹出错误对话框,文本内容“账号密码不匹配,是否重新登录”,给定两个…...

Meta分析核心技术
Meta分析是针对某一科研问题,根据明确的搜索策略、选择筛选文献标准、采用严格的评价方法,对来源不同的研究成果进行收集、合并及定量统计分析的方法,最早出现于“循证医学”,现已广泛应用于农林生态,资源环境等方面。…...

Gof23设计模式之责任链模式
1.概述 责任链模式又名职责链模式,为了避免请求发送者与多个请求处理者耦合在一起,将所有请求的处理者通过前一对象记住其下一个对象的引用而连成一条链;当有请求发生时,可将请求沿着这条链传递,直到有对象处理它为止…...

数字孪生和元宇宙:打造未来的数字边界
数字孪生和元宇宙是近两年来被热议的两个概念,但由于技术的交叉两者也极易被混淆。本文希望带大家深入探讨一下这两者之间的关系,以及它们如何一起构建了数字时代的新格局。 1. 数字孪生的本质 数字孪生是一种虚拟模型,它通过数字手段对现实…...

【新版】系统架构设计师 - 软件架构设计<新版>
个人总结,仅供参考,欢迎加好友一起讨论 文章目录 架构 - 软件架构设计<新版>考点摘要概念架构的 4 1 视图架构描述语言ADL基于架构的软件开发方法ABSDABSD的开发模型ABSDMABSD(ABSDM模型)的开发过程 软件架…...

Linux面试题
当准备 Linux 面试时,以下是一些可能会遇到的常见 Linux 面试题: 1. 什么是Linux?解释一下Linux操作系统的特点。 2. 什么是Linux内核?Linux内核的作用是什么? 3. 如何在Linux系统上查看当前的IP地址和子网掩码&#…...

NODEJS版本管理工具
一、使用NVM 下载 Linux下载 curl -o- https://raw.githubusercontent.com/nvm-sh/nvm/v0.39.0/install.sh widows下载地址 https://github.com/coreybutler/nvm-windows/releases 安装Node.js版本: nvm install 14.16.0 切换Node.js版本: nvm use …...

【个人笔记本】本地化部署 类chatgpt模型 详细流程
不推荐小白,环境配置比较复杂 全部流程 下载原始模型:Chinese-LLaMA-Alpaca-2linux部署llamacpp环境使用llamacpp将Chinese-LLaMA-Alpaca-2模型转换为gguf模型windows部署Text generation web UI 环境使用Text generation web UI 加载模型并进行对话 准…...

RFID与人工智能怎么融合,RFID与人工智能融合的应用
随着物联网技术的不断发展,现实世界与数字世界的桥梁已经被打通。物联网通过各种传感器,将现实世界中的光、电、热等信号转化为有价值的数据。这些数据可以通过RFID技术进行自动收集和传输,然后经由人工智能算法进行分析、建模和预测…...
性能测试 —— Jmeter 常用三种定时器
1、同步定时器 位置:HTTP请求->定时器->Synchronizing Timer 当需要进行大量用户的并发测试时,为了让用户能真正的同时执行,添加同步定时器,用户阻塞线程,知道线程数达到预先配置的数值,才开始执行…...

每个高级前端工程师都应该知道的前端布局
首发于公众号 大迁世界,欢迎关注。📝 每周一篇实用的前端文章 🛠️ 分享值得关注的开发工具 😜 分享个人创业过程中的趣事 快来免费体验ChatGpt plus版本的,我们出的钱 体验地址:https://chat.waixingyun.cn 可以加入网站底部技术群,一起找bug,另外新版作图神器已上线…...

100道基于Android毕业设计的选题题目,持续更新
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝30W,Csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 大家好,我是程序员徐师兄、今天给大家谈谈基于android的app开发毕设题目,以及基于an…...
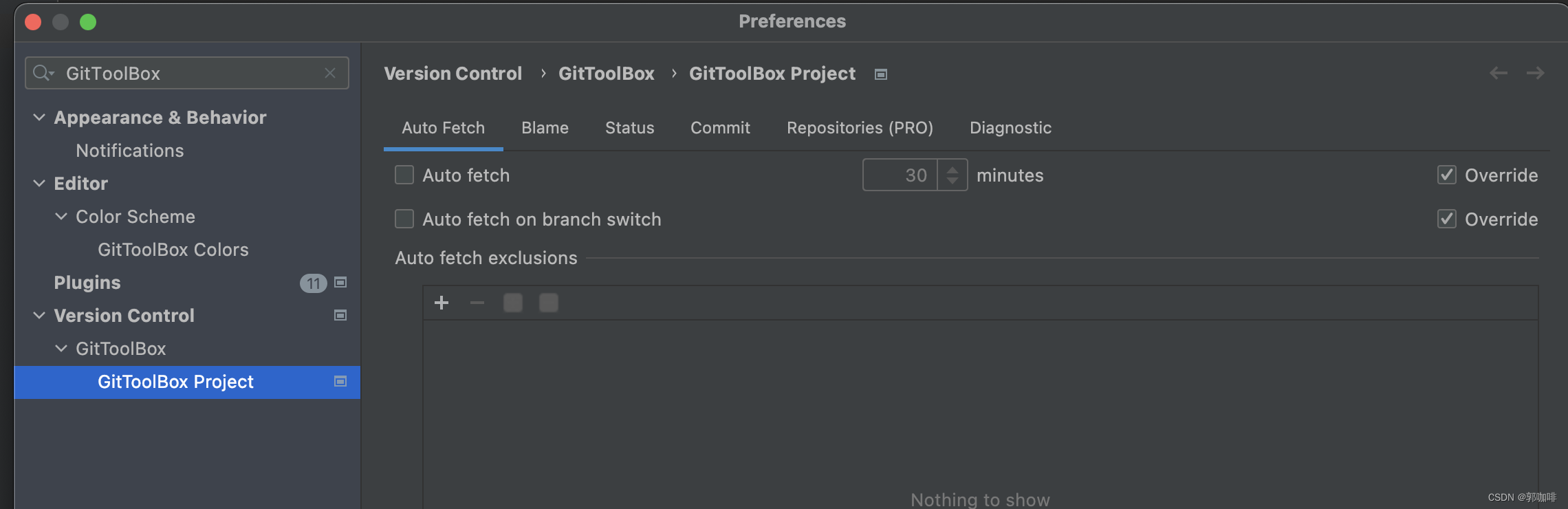
idea显示git分支信息(GitToolBox插件)
效果图 说明 本身idea在右下角会有git分支信息,但是显示的当前打开文件的分支信息,并且不够显眼 解决 1、安装插件(GitToolBox插件) 2、修改idea.properties project.tree.structure.show.urlfalse ide.tree.horizontal.default.autoscrollingfalse将…...

Hadoop知识点之Hadoop发展历程
一、Hadoop名字的起源 Hadoop这个名字不是一个缩写,它是一个虚构的名字。 该项目的创建者,Doug Cutting如此解释Hadoop: 这个名字是我孩子给一头吃饱了的棕黄色大象命名的。我的命名标准就是简短,容易发音和拼写,没有…...

阿里云无影电脑:免费体验无影云电脑3个月
阿里云无影云电脑免费领取流程,免费无影云电脑配置为4核8G,可以免费使用3个月,阿里云百科分享阿里云无影云电脑(云桌面)免费申请入口、申请流程及免费使用限制条件说明: 目录 阿里云无影云电脑免费申请入…...
:面向对象)
菜鸟教程《Python 3 教程》笔记(20):面向对象
菜鸟教程《Python 3 教程》笔记(20) 20 面向对象20.1 面向对象技术简介20.2 创建类20.2.1 类定义20.2.2 实例化20.2.3 初始化20.2.4 类变量、实例变量20.2.5 类方法、实例方法、静态方法 20.3 访问可见性20.3.1 property装饰器 20.4 动态性20.4.1 __slot…...
vue2编辑markdown
效果 npm i mavon-editor --save 只能全局注册 使用...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

DAY 45 超大力王爱学Python
来自超大力王的友情提示:在用tensordoard的时候一定一定要用绝对位置,例如:tensorboard --logdir"D:\代码\archive (1)\runs\cifar10_mlp_experiment_2" 不然读取不了数据 知识点回顾: tensorboard的发展历史和原理tens…...
