高斯公式证明
高斯公式:
若空间闭区域 Ω \Omega Ω 由光滑的闭曲面 Σ \Sigma Σ 围成,则
∫ ∫ ∫ Ω ( ∂ P ∂ x + ∂ Q ∂ y + ∂ R ∂ z ) d v = ∮ ∮ Σ P d y d z + Q d z d x + R d x d y \int \int \int _{\Omega}(\frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z})dv = \oint \oint _{\Sigma} P dy dz + Q dzdx + R dxdy ∫∫∫Ω(∂x∂P+∂y∂Q+∂z∂R)dv=∮∮ΣPdydz+Qdzdx+Rdxdy
证明:
空间光滑的闭区域一定可以被分割,设 x 1 ( y , z ) 和 x 2 ( y , z ) 是 Ω x_1(y,z)和x_2(y,z)是\Omega x1(y,z)和x2(y,z)是Ω的左右边界,根据三重积分可得:
∫ ∫ ∫ Ω ∂ P ∂ x d v = ∫ ∫ D y z ∫ x 1 ( y , z ) x 2 ( y , z ) ∂ P ( x , y , z ) ∂ x d x d y d z = ∫ ∫ D y z P ( x 2 ( y , z ) , y , z ) d y d z − ∫ ∫ D y z P ( x 1 ( y , z ) , y , z ) d y d z \int \int \int _{\Omega} \frac{\partial P}{\partial x} dv = \int \int _{D_{yz}} \int _{x_1(y,z)}^{x_2(y,z)}\frac{\partial P(x,y,z)}{\partial x}dx dy dz = \\ \int \int _{D_{yz}} P(x_{2}(y,z),y,z)dydz - \int \int _{D_{yz}} P(x_{1}(y,z),y,z)dydz ∫∫∫Ω∂x∂Pdv=∫∫Dyz∫x1(y,z)x2(y,z)∂x∂P(x,y,z)dxdydz=∫∫DyzP(x2(y,z),y,z)dydz−∫∫DyzP(x1(y,z),y,z)dydz
同理,根据闭区域曲面积分,闭区域可以被分为左右两部分(设左边部分为 Σ 1 \Sigma_1 Σ1右边部分为 Σ 2 \Sigma_2 Σ2)分别计算曲面积分:
∮ Σ ∮ P d y d z = ∮ Σ 2 ∮ P d y d z − ∮ Σ 1 ∮ P d y d z = ∫ ∫ D y z P ( x 2 ( y , z ) , y , z ) d y d z − ∫ ∫ D y z P ( x 1 ( y , z ) , y , z ) d y d z \color{red} \oint _{\Sigma}\oint P dy dz = \oint _{\Sigma_{2} }\oint P dy dz - \oint _{\Sigma_{1} }\oint P dy dz = \\ \int \int _{D_{yz}} P(x_{2}(y,z),y,z)dydz - \int \int _{D_{yz}} P(x_{1}(y,z),y,z)dydz ∮Σ∮Pdydz=∮Σ2∮Pdydz−∮Σ1∮Pdydz=∫∫DyzP(x2(y,z),y,z)dydz−∫∫DyzP(x1(y,z),y,z)dydz
高斯公式得证。
相关文章:

高斯公式证明
高斯公式: 若空间闭区域 Ω \Omega Ω 由光滑的闭曲面 Σ \Sigma Σ 围成,则 ∫ ∫ ∫ Ω ( ∂ P ∂ x ∂ Q ∂ y ∂ R ∂ z ) d v ∮ ∮ Σ P d y d z Q d z d x R d x d y \int \int \int _{\Omega}(\frac{\partial P}{\partial x} \frac{\p…...

速卖通获得aliexpress商品详情 API 返回值说明
item_get-获得aliexpress商品详情 aliexpress.item_get 进入测试 公共参数 名称类型必须描述keyString是调用key(必须以GET方式拼接在URL中)secretString是调用密钥api_nameString是API接口名称(包括在请求地址中)[item_search…...

c++语法-模板
模板 模板是C中一种强大的特性,允许你编写通用的代码,以便在不同数据类型上重复使用。模板分为函数模板和类模板,它们都是在编译时生成具体代码的蓝图。 函数模板 函数模板是一种定义通用函数的方式,可以在不同数据类型上使用相…...
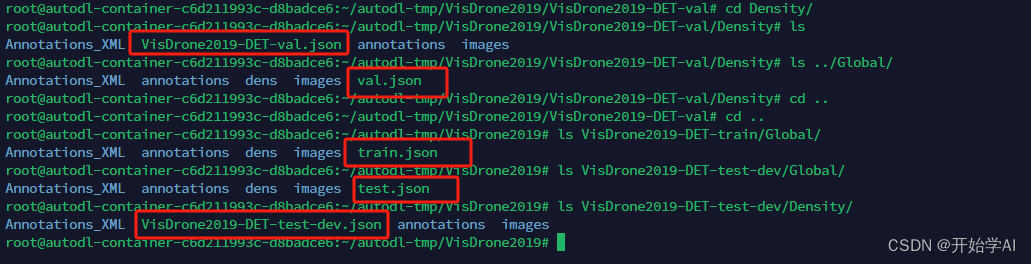
DMNet复现(一)之数据准备篇:Density map guided object detection in aerial image
一、生成密度图 密度图标签生成 采用以下代码,生成训练集密度图gt: import cv2 import glob import h5py import scipy import pickle import numpy as np from PIL import Image from itertools import islice from tqdm import tqdm from matplotli…...

k8s相关命令-命名空间
k8s相关命令目录 文章目录 前言一、创建命名空间二、删除命名空间三、查看命名空间列表四、查看命名空间列表五、查看特定命名空间下所有资源六、删除特定命名空间下所有资源 前言 记录k8s命名空间的相关操作命令 一、创建命名空间 kubectl create namespace <namespace&g…...

CG Magic分享同一场景里下,VR渲染器和CR渲染器哪个好?
渲染操作时,VR渲染器和CR渲染器的对比成为常见问题了。这个问题很多人都会问。 今天CG Magic小编通过一个真实的项目,就是同一场景下来比较一下VR渲染器和CR渲染器的区别。 以下图为例是用来测试的场景当年的最终图。采用了当年的一个伊丽莎白大街152号的…...
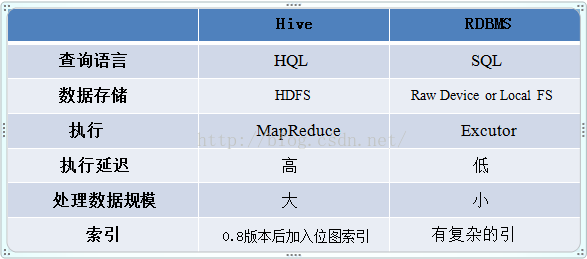
Hive工作原理
Hive 工作原理详解-阿里云开发者社区 Hive的服务端组件 1. Driver组件:该组件包括:Compiler、Optimizer、Executor,它可以将Hive的编译、解析、优化转化为MapReduce任务提交给Hadoop1中的JobTracker或者是Hadoop2中的SourceManager来进行实际的执行相应…...

vue 使用this.$set设置对象属性值时,不更新试图
vue 使用this.$set设置对象属性值时,不更新试图。 后来发现是因为若对象中存在该属性时,只更新值,不添加响应监测。 //vue/src/core/observer/index.js 源码片段/*** Set a property on an object. Adds the new property and* triggers ch…...
uniapp视频播放功能
UniApp提供了多种视频播放组件,包括视频播放器(video)、多媒体组件(media)、WebView(内置Video标签)等。其中,video和media组件是最常用的。 video组件 video组件是基于HTML5 vide…...

Java面向对象七大原则以及设计模式单例模式和工厂模式简单工厂模式
面向对象的七大原则(OOP) 1,开闭原则: 对扩展开发,对修改关闭 2.里氏替换原则: 继承必须确保超类所拥有的子类的性质在子类中仍然成立 3.依赖倒置原则: 面向接口编程,不要面向实现编程&am…...

Linux 遍历目录(cd 命令)
Linux 遍历目录(cd 命令) 文章目录 Linux 遍历目录(cd 命令)一、cd 命令二、绝对文件路径三、相对文件路径 一、cd 命令 在 Linux 文件系统上,可以使用 cd 命令将 shell 会话切换到另一个目录。cd 命令的格式也很简单…...
整合Nginx实现反向代理
针对后端启动多个服务,接口需要统一请求路径时,可以使用nginx进行请求地址反向代理。 1.下载: nginx 2.下载完成后解压,找到配置文件nginx.conf(在解压文件的conf目录中),在http中增加以下示例代码&#x…...

Linux:IP转INT详解
一、IP地址介绍 IP地址(Internet Protocol Address)是指互联网协议地址,是所有连接到网络设备的唯一标识符。IP地址由32位二进制数表示,通常以四段十进制数(每个数值范围为0-255)表示,例如192.1…...
43.MQ—RabbitMQ
目录 一、MQ—RabbitMQ。 (1)同步调用与异步调用。 (1.1)同步调用。 (1.2)异步调用。 (2)MQ之间的区别。 (3)RabbitMQ学习。 (3.1…...
)
Leetcode154. 寻找旋转排序数组中的最小值(存在重复元素)
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums [0,1,4,4,5,6,7] 在变化后可能得到:…...

docker查看镜像的latest对应的具体版本
查询容器镜像时,TAG只显示latest,而不是显示具体的版本号 docker images # 显示内容 REPOSITORY TAG IMAGE ID CREATED SIZE nginx latest 605c77e624dd 20 months ago 141MB redis latest 7614ae945…...
RabbitMQ深入 —— 死信队列
前言 前面荔枝梳理了RabbitMQ中的普通队列、交换机以及相关的知识,在这篇文章中荔枝将会梳理RabbitMQ的一个重要的队列 —— 死信队列,主要了解消息流转到死信队列的三种的方式以及相应的实现demo。希望能帮助到有需要的小伙伴~~~ 文章目录 前言 死信队…...

【React + Umi】自定义离开页面拦截弹框事件
在 react umi 中对离开页面的行为进行自定义弹窗拦截控制。以下为可选的方案分析。 wrapper 首先,因为项目框架是 umi,最先想到了 umi 路由的 wrapper 装饰器,但仔细一想又不太对, wrapper 争对于跳转到某个特定页面的前置行为…...
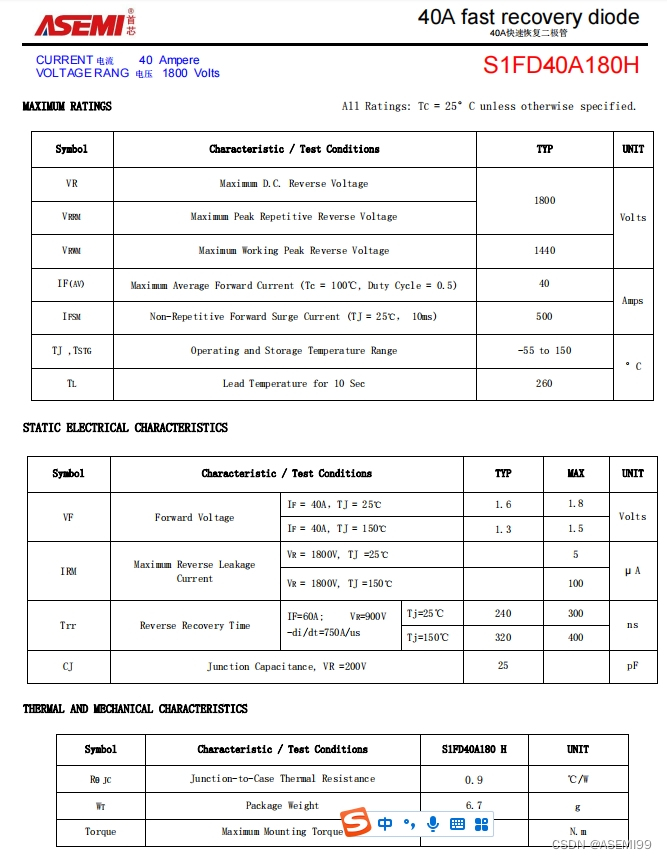
S1FD40A180H-ASEMI快恢复二极管S1FD40A180H
编辑:ll S1FD40A180H-ASEMI快恢复二极管S1FD40A180H 型号:S1FD40A180H 品牌:ASEMI 封装:TO-247 特性:大功率、快恢复二极管 正向电流:40A 反向耐压:1800V 恢复时间:<300n…...
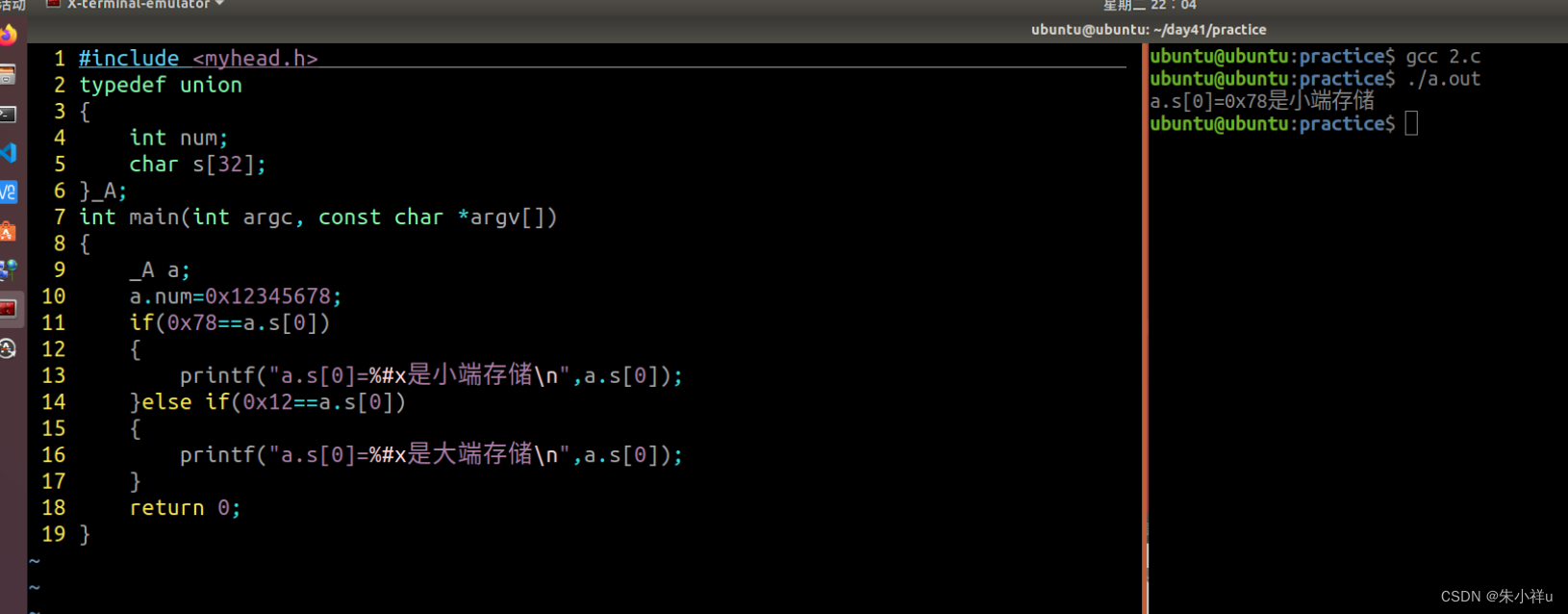
网络编程 day1
1->x.mind网络编程基础 2->简述字节序的概念,并用共用体(联合体)的方式计算本机的字节序 1.字节序是指不同类型的CPU主机,内存存储多字节整数序列的方式 2.小端字节序:低序字节存储在低地址上 3.大端字节序&a…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...
