【操作系统笔记】内存分配
内存对齐
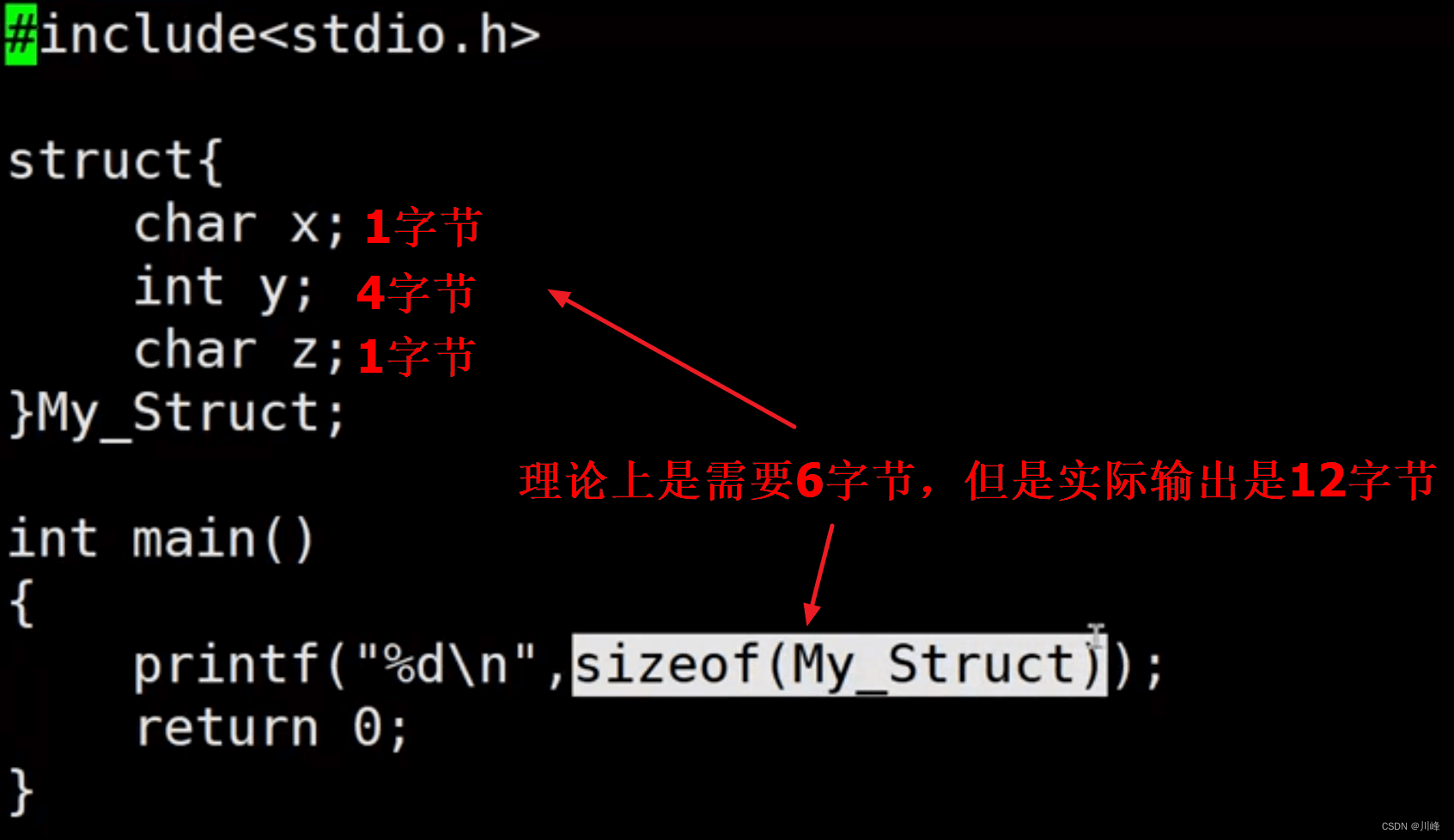
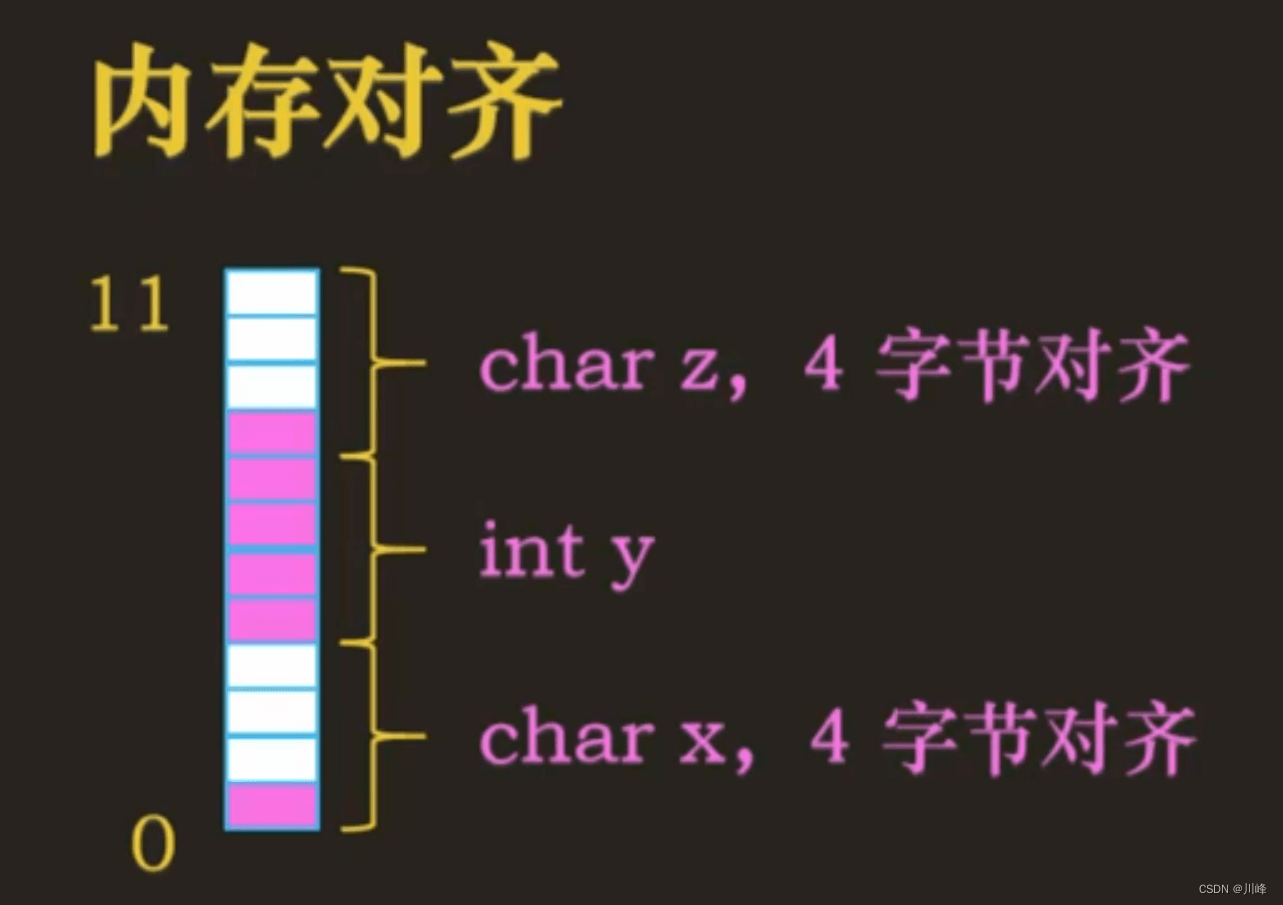
问题:为什么需要内存对齐呢?
-
主要原因是为了兼容,为了让程序可以运行在不同的处理器中,有很多处理器在访问内存的时候,只能从特定的内存地址读取数据。换个说法就是处理器每次只能从内存取出特定个数字节的数据。
-
如果不做内存对齐的话,CPU 访问一个变量的值有可能需要跨两个内存块(假设每4字节为一块)就需要访问 2 次,损耗 CPU 性能,内存对齐后,CPU 只需要一次访问就可以读取 4 字节数据。
比如说一次只能读取 4 个字节的数据,那么处理器只能访问的地址必须是 4 的倍数,比如 0x0、0x4、0x8、0x12等等。
如果内存不对齐的话,会有什么影响?
- 那一个变量的值可能跨两个内存块,那么 CPU 就需要访问两次,损耗 CPU 性能。

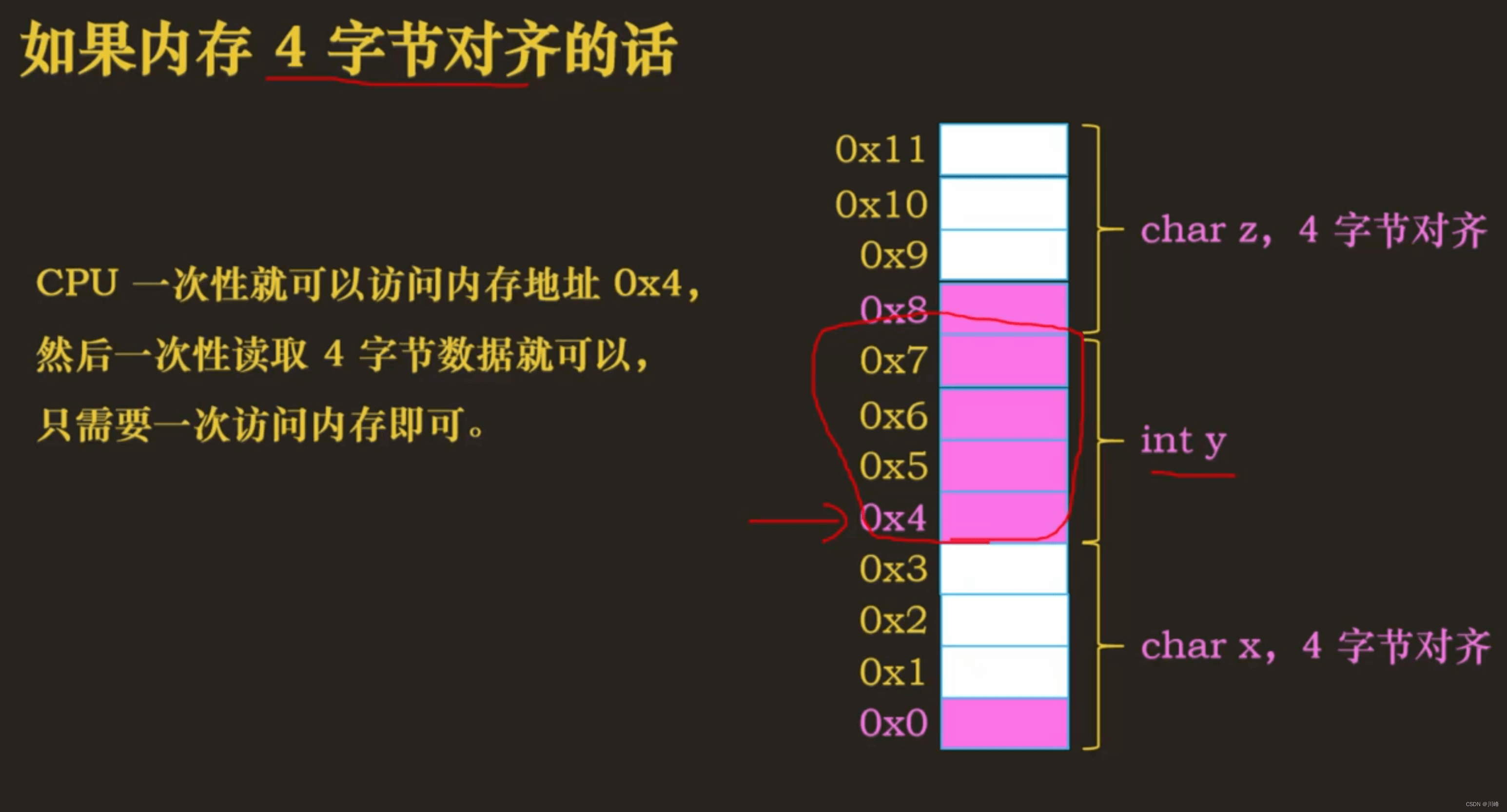
关于内存对齐需要知道的事情:
-
如果程序只是运行在 AMD64 和 x86 处理器上,是不需要考虑内存对齐的
因为 AMD64 处理器可以读取任何小于等于 8 字节的变量,x86 可以读取任何小于等于 4 字节的变量。
-
但是,为了使的程序可以兼容其他的处理器,一般都会考虑内存对齐
-
采用了内存对齐技术,即保证无论 CPU 一次取几个字节(1、2、4、8、16…)只要所取的变量大小小于一次可读取的字节数,就不会访问两次内存。
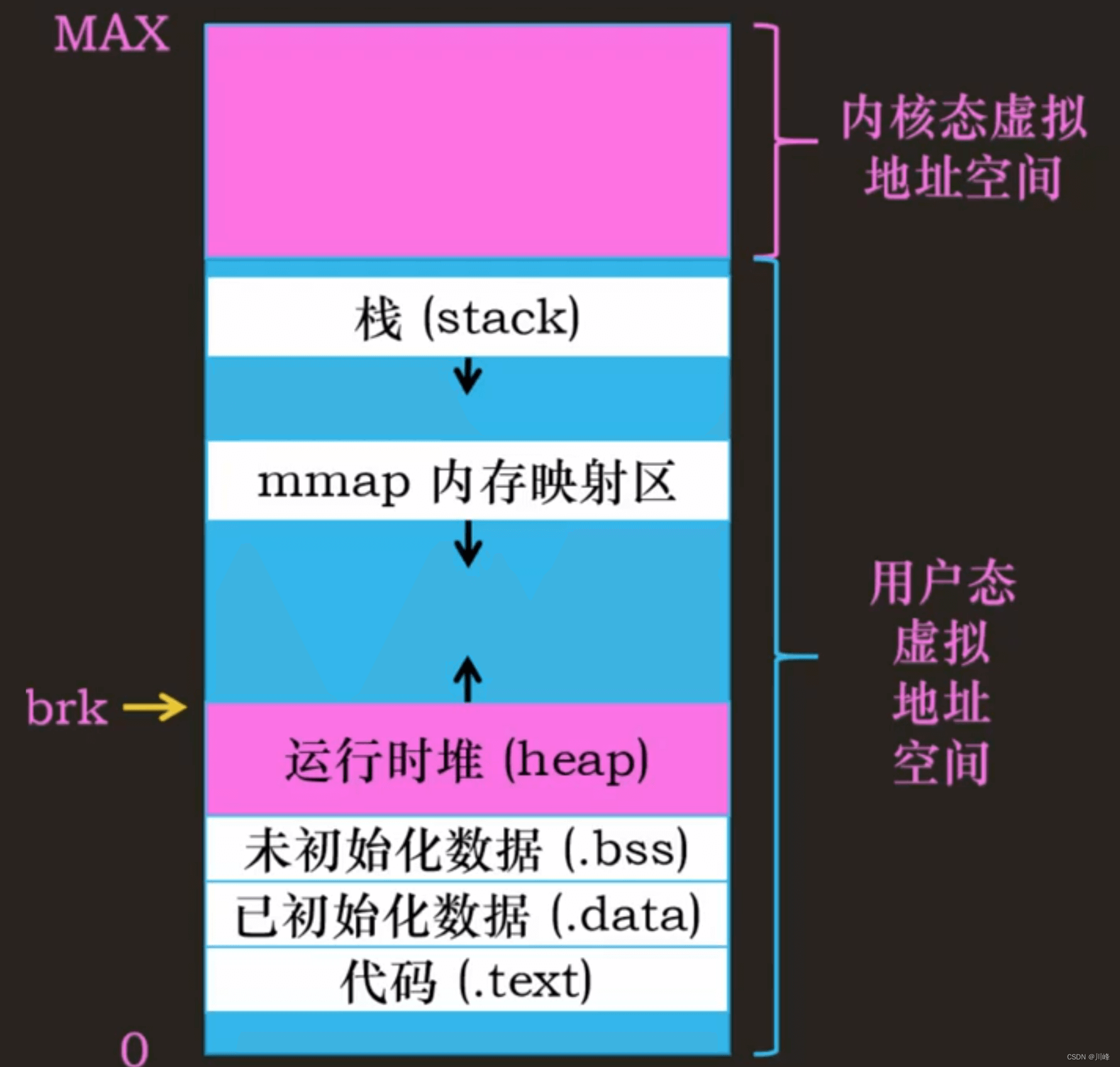
用户态虚拟内存分配和释放
malloc 和 free
malloc 和 free 用于程序在用户态下、申请和释放堆内存,所谓的堆内存,其实就是运行时堆区域的一段虚拟地址空间。虚拟地址数量也是有限的,不合理分配的话会很快的就用完了,也就发生 OOM 了。
提高虚拟内存的利用率,也就是用过的虚拟地址,释放后,可以重复分配使用。分配和释放的时间复杂度,吞吐率要高。
申请堆内存的方法有两个:
- ① mmap:通过增加内存映射来申请堆内存
- ② sbrk: 通过改变 brk 来申请堆内存
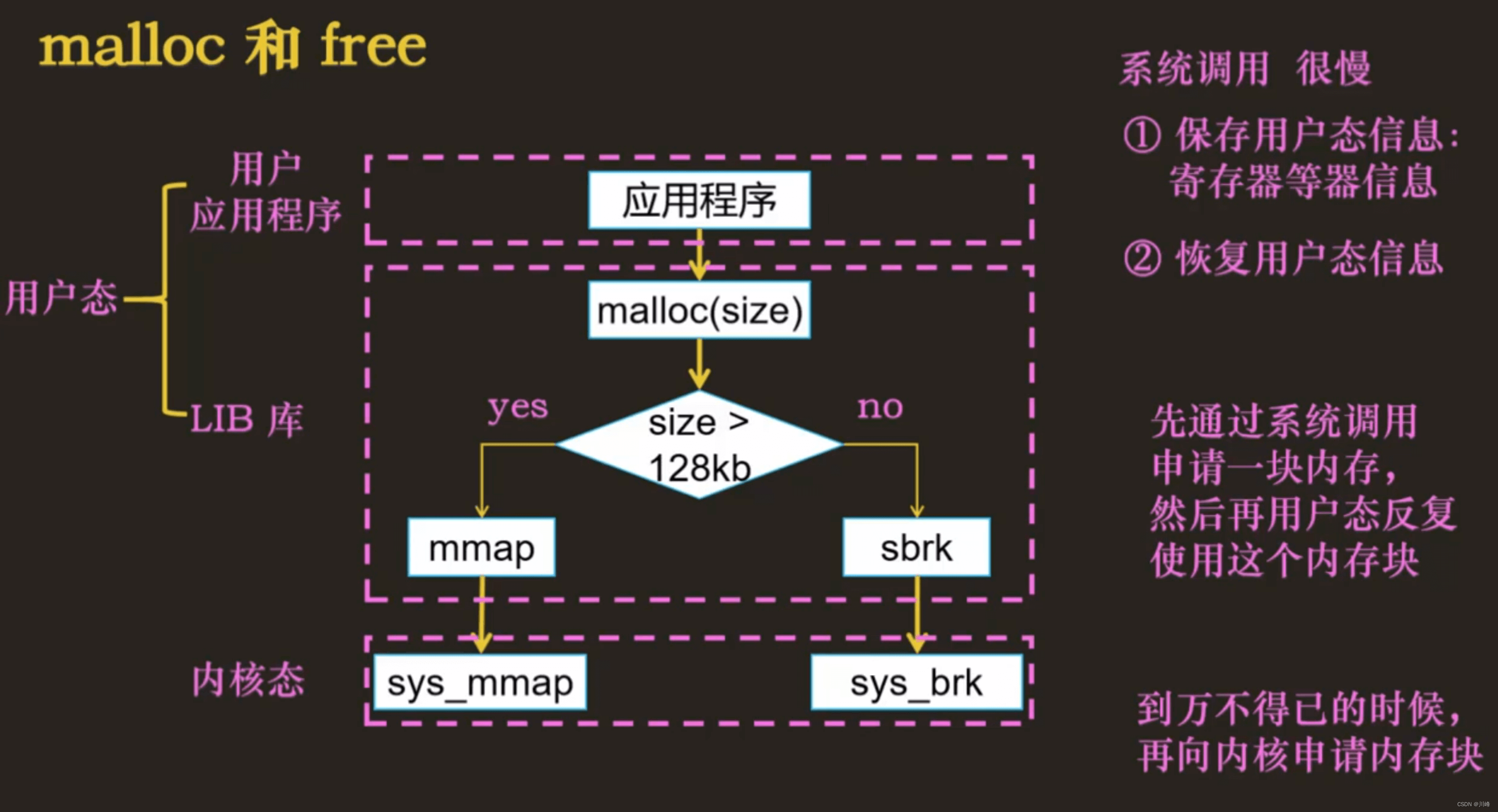


malloc 和 free 的全流程解析:https://www.processon.com/view/link/62384ce70e3e74074cf4ebae
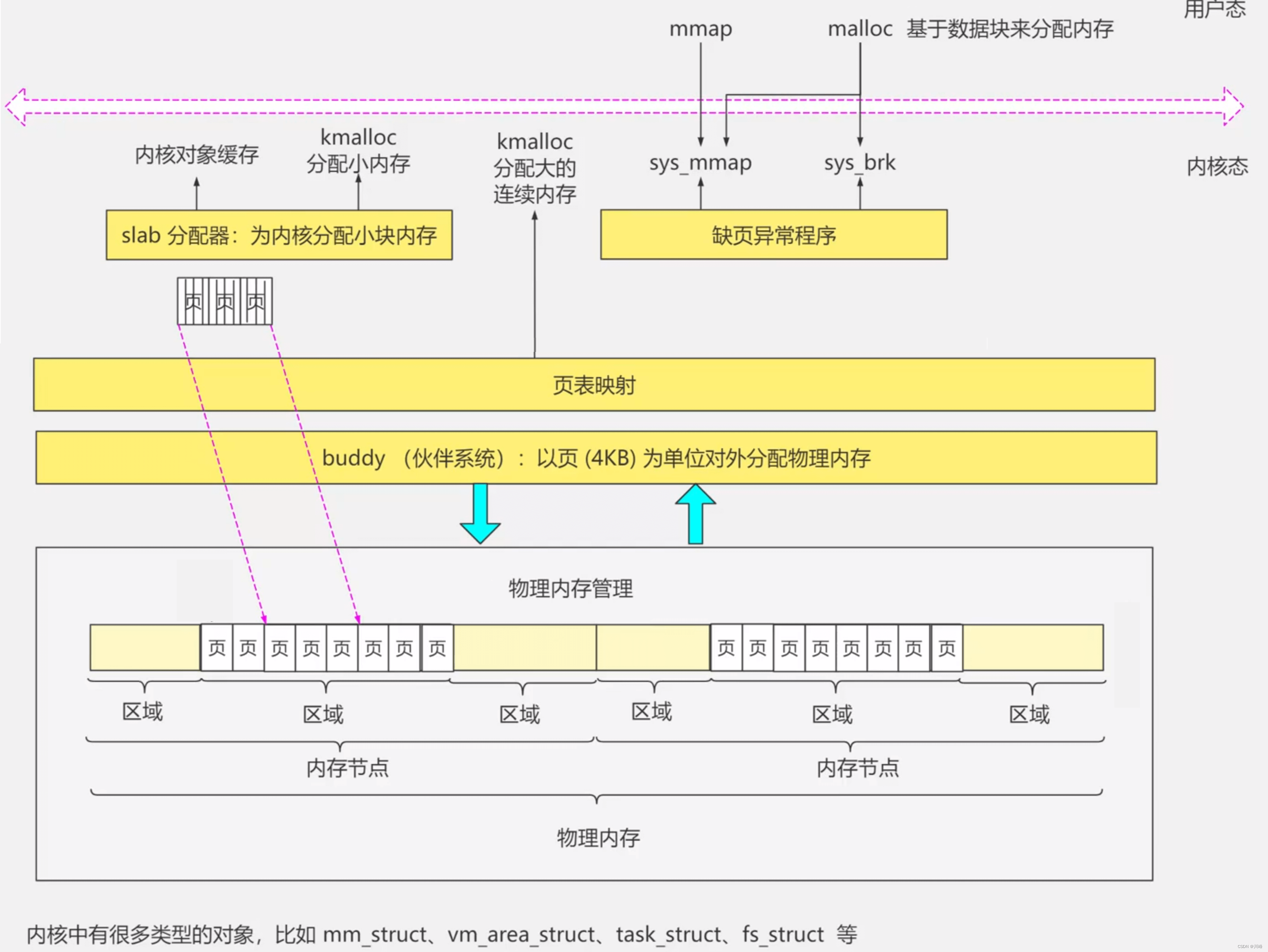
用户态和内核态内存分配
用户态通过mmap和malloc申请分配得到的内存都是虚拟内存地址,只有当 CPU 访问该地址时,发现对应的物理页号不存在,发生缺页异常,此时才会真正的分配物理内存,这是由缺页异常处理程序分配物理页号到虚拟页表来完成的。
相关文章:

【操作系统笔记】内存分配
内存对齐 问题:为什么需要内存对齐呢? 主要原因是为了兼容,为了让程序可以运行在不同的处理器中,有很多处理器在访问内存的时候,只能从特定的内存地址读取数据。换个说法就是处理器每次只能从内存取出特定个数字节的数…...

Web 整合
HTML span 行内元素 p 块级元素 br/ 强制换行 i em倾斜 b strong 加粗 u 下划线 mark 高亮 超链接 a :a href"链接地址" target"_blank" alt"可替文本" title"文字提示" tartget:_self 自己界面打开 _…...

hasOwnProperty 方法解析
一、含义: hasOwnProperty 是 JavaScript 中的一个内置方法,用于检查对象是否具有指定名称的属性。 具体来说,hasOwnProperty 方法用于判断一个对象是否拥有某个指定的属性,而不是继承自原型链的属性。它是一个布尔值方法&#…...

使用 nohup 运行 Python 脚本
简介:在数据科学、Web 开发或者其他需要长时间运行的任务中,我们经常需要让 Python 脚本在后台运行。尤其是在远程服务器上,可能因为网络不稳定或需要执行多个任务,我们不希望 Python 脚本因为终端关闭而被终止。这时,…...
Django:五、登录界面实现动态图片验证码
一、下载包 pip install pillow 二、代码 这是一个函数,无输入,返回两个值。一个值是图片,一个值是图片中的数字及字母。 需要注意:font_fileMonaco.ttf 是一个验证码字体文件,如有需要,可三连私信。 …...
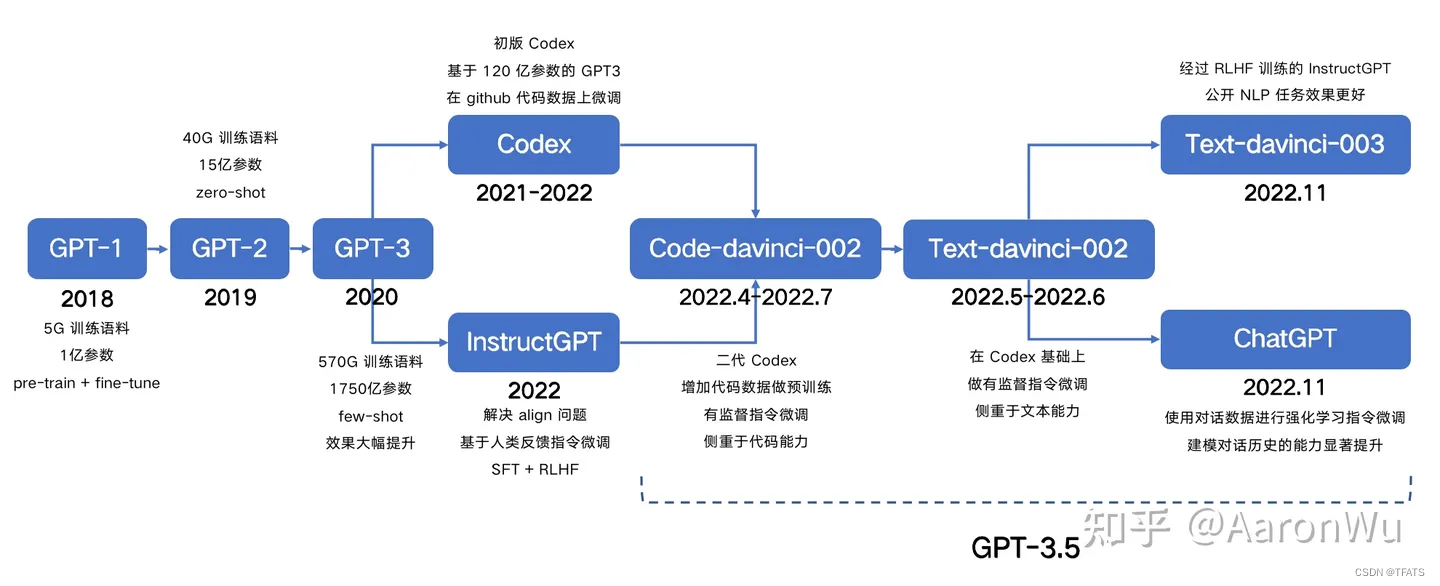
GPT,GPT-2,GPT-3,InstructGPT的进化之路
ChatGPT 火遍圈内外,突然之间,好多人开始想要了解 NLP 这个领域,想知道 ChatGPT 到底是个什么?作为在这个行业奋斗5年的从业者,真的很开心让人们知道有一群人在干着这么样的一件事情。这也是我结合各位大佬的文章&…...
)
firefox_dev_linux下载安装配置(部分系统自带包请看结尾)
download 从 Firefox 的官方网站下载 Firefox Developer Edition 的 tar 文件 firefox_dev_linux_download # 终端快速下载 wget https://download.mozilla.org/?productfirefox-devedition-latest-ssl&oslinux64&langen-US彻底删除自带原版 # apt系 sudo apt --pu…...
vim缓存-交换文件
Catf1agCTF靶场 web swp 题目链接:http://catf1ag.cn/ 个人博客:https://sword-blogs.com/ 题目考点: vim在编辑文档的过程中如果异常退出,会产生缓存文件 vim 交换文件名 参考文章:vim手册 https://yianwillis.…...
Hive 优化建议与策略
目录 编辑 一、Hive优化总体思想 二、具体优化措施、策略 2.1 分析问题得手段 2.2 Hive的抓取策略 2.2.1 策略设置 2.2.2 策略对比效果 2.3 Hive本地模式 2.3.1 设置开启Hive本地模式 2.3.2 对比效果 2.3.2.1 开启前 2.3.2.2 开启后 2.4 Hive并行模式 2.5 Hive…...
CentOS 7.5 centos failed to load selinux policy 错误解决方法
这是个 selinux 使能导致的, 关闭即可 在进入到内核选中界面,选中要启动的内核, 按键盘 e 就会进入启动参数界面 进入启动参数界面如图,按上下键找到 UTF8 UTF8如图, 添加 selinux0 添加完成如图, 按 ctr…...
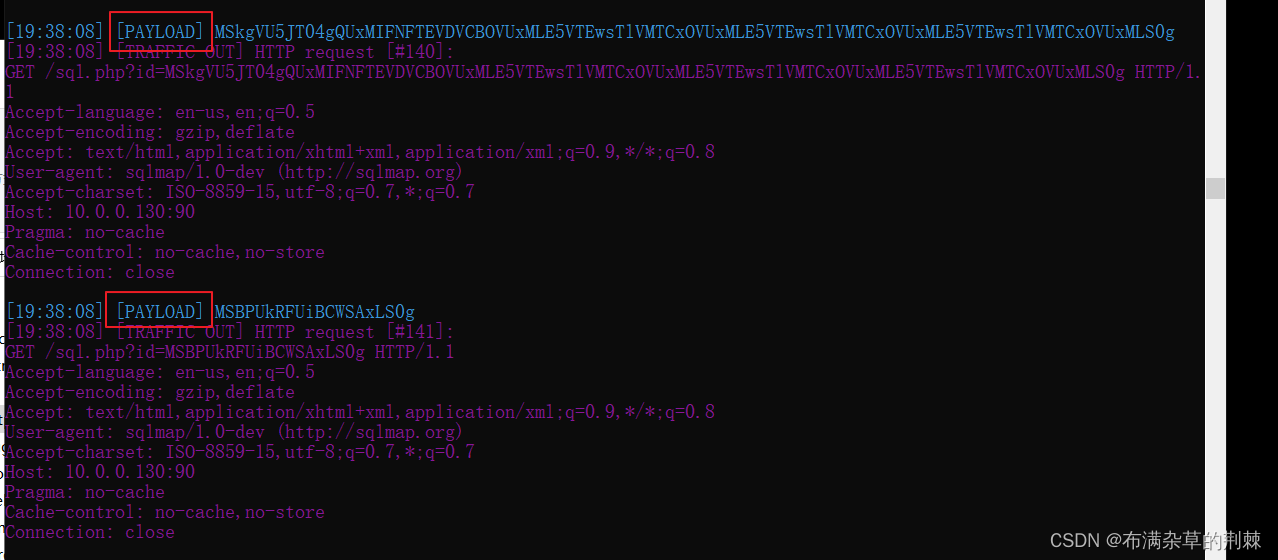
注入之SQLMAP(工具注入)
i sqlmap是一个自动化的SQL注入工具,其主要功能是扫描,发现并利用给定的URL和SQL注入漏洞,其广泛的功能和选项包括数据库指纹,枚举,数据库提权,访问目标文件系统,并在获取操作权限时执行任…...

Linux学习资源Index
由于Linux是支撑“云计算”的最核心、最底层、最重要的技术,持续提升自已的Linux水平是必须的,这里将不断更新的Linux学习索引。 书籍 书籍首页 - Documentation (rockylinux.org) WWW链接 提定发行版 RockyLinux Rocky Linux Download Rocky | R…...

什么是SVG(可缩放矢量图形)?它与普通图像格式有何不同?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 什么是SVG?⭐ 与普通图像格式的不同⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 欢迎来到前端入门之旅!感兴趣的可以订阅本专栏哦!这个专栏是为那些对Web开发感兴趣、刚刚…...

求生之路2服务器搭建插件安装及详细的游戏参数配置教程windows
求生之路2服务器搭建插件安装及详细的游戏参数配置教程windows 大家好我是艾西,最近研究了下 l4d2(求生之路2)这款游戏的搭建以及架设过程。今天就给喜欢l4d2这款游戏的小伙伴们分享下怎么搭建架设一个自己的服务器。毕竟自己当服主是热爱游…...

React TypeScript 定义组件的各种方式
目录 举例说明1. 使用 class 定义2. 使用函数定义2.1 使用普通函数2.2 使用函数组件 举例说明 比如我们要定义一个计数器 Counter,它包含一个 label 和一个 button,计数器的初始值由外部传入,点击 button 计数加 1: 这虽然是个简单组件&…...
)
互联网摸鱼日报(2023-09-20)
互联网摸鱼日报(2023-09-20) 36氪新闻 国货美妆这五年:押注头部主播,追求极致流量中遭反噬 处于水深火热之中的奈飞该如何自救? 一头“灰犀牛”将冲击美国 年轻人花钱的样子变了 金V之后再推橙V,微博正试图重建创作者生态 …...

AWS入列CNCF基金会
7月27日,IT之家曾经报道,微软加入Linux旗下CNCF基金会,在这之后不到一个月的今天,亚马逊AWS也宣布,以铂金身份加入此基金会。 CNCF,全称Cloud Native Computing Fundation,该基金会旨在使得容器…...

岭回归与LASSO回归:解析两大经典线性回归方法
文章目录 🍋引言🍋岭回归(Ridge Regression)🍋实战---岭回归🍋LASSO回归(LASSO Regression)🍋实战---LASSO回归🍋岭回归和LASSO哪个更容易是直线🍋…...
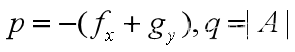
数学建模——微分方程介绍
一、基础知识 1、一阶微分方程 称为一阶微分方程。y(x0)y0为定解条件。 其常规求解方法: (1)变量分离 再两边积分就可以求出通解。 (2)一阶线性求解公式 通解公式: 有些一阶微分方程需要通过整体代换…...

Minio入门系列【7】Spring Boot集成Minio
1 前言 之前介绍了如何使用Minio提供的JAVA SDK进行上传和下载文件,在此基础上,我们可以使用spring boot集成Minio JAVA SDK,添加自动配置、装配、客户端管理等功能,简化开发 2 Spring Boot集成Minio 2.1 环境搭建 首先我们搭…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...
