【算法基础】数学知识
质数
质数的判定
866. 试除法判定质数 - AcWing题库
时间复杂度是logN
#include<bits/stdc++.h>
using namespace std;
int n;
bool isprime(int x)
{if(x<2) return false;for(int i=2;i<=x/i;i++){if(x%i==0) return false;}return true;
}
signed main()
{cin>>n; for(int i=1;i<=n;i++){int x;cin>>x;if(isprime(x)) puts("Yes");else puts("No");}return 0;
} 分解质因数
867. 分解质因数 - AcWing题库
#include<bits/stdc++.h>
using namespace std;
int n;
void divide(int x)
{for(int i=2;i<=x/i;i++){if(x%i==0) {int s=0;while(x%i==0) x/=i,s++;cout<<i<<" "<<s<<endl;}}if(x>1) cout<<x<<" "<<1<<endl;cout<<endl;
}
signed main()
{cin>>n; for(int i=1;i<=n;i++){int x;cin>>x;divide(x);}return 0;
} 筛质数(用线性筛,O(N)
868. 筛质数 - AcWing题库
朴素版,埃氏筛法
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
bool st[N];
int prime[N],cnt;
int n;
void getprimes(int x)
{for(int i=2;i<=x;i++){if(st[i]) continue;prime[cnt++]=i;for(int j=i+i;j<=x;j+=i) st[j]=true;}}
signed main()
{cin>>n; getprimes(n);cout<<cnt;return 0;
} 线性筛
868. 筛质数 - AcWing题库
线性筛把时间复杂度优化到O(n),就需要保证筛去一个数只用一次,保证最小质因数就可以确保这一点。
如。筛去24,24=2*12,24=3*8,显然这里2是最小质因数,如何确保不筛去3*8?
这里3*8=3*2*4,即i包含上一个prime,直接break。
只要i包含了prime就不能保证最小质因数!!
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
bool st[N];
int prime[N],cnt;
int n;
void getprimes(int x)
{for(int i=2;i<=x;i++){if(!st[i]) prime[cnt++]=i;for(int j=0;prime[j]<=x/i;j++){st[prime[j]*i]=true;if(i%prime[j]==0) break;}}}
signed main()
{cin>>n; getprimes(n);cout<<cnt;return 0;
} 约数
试除法求一个数的所有约束
869. 试除法求约数 - AcWing题库
#include<bits/stdc++.h>
using namespace std;void solve(int x)
{stack<int> s;for(int i=1;i<=x/i;i++){if(x%i==0) {cout<<i<<' ';if(i!=x/i) s.push(x/i);}}while(s.size()){cout<<s.top()<<" ";s.pop();}puts("");
}
signed main()
{int n;cin>>n;while(n--){int x;cin>>x;solve(x);}return 0;
} 约数个数//约数之和
870. 约数个数 - AcWing题库

#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
typedef long long LL;
signed main()
{int n;cin>>n;unordered_map<int,int> mp;while(n--){int x;cin>>x;for(int i=2;i<=x/i;i++){while(x%i==0){mp[i]++;x/=i;}}if(x>1) mp[x]++;}LL res=1;for(auto p:mp) res=res*(p.second+1)%mod;cout<<res<<endl; return 0;
} 871. 约数之和 - AcWing题库
#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
typedef long long LL;
signed main()
{int n;cin>>n;unordered_map<int,int> mp;while(n--){int x;cin>>x;for(int i=2;i<=x/i;i++){while(x%i==0){mp[i]++;x/=i;}}if(x>1) mp[x]++;}LL res=1;for(auto p:mp){LL a=p.first,b=p.second;LL t=1;while(b--) t=(t*a+1)%mod;//秦九韶res=res*t%mod; }cout<<res<<endl; return 0;
} 最大公约数
872. 最大公约数 - AcWing题库
#include<bits/stdc++.h>
using namespace std;
int gcb(int a,int b)
{return b?gcd(b,a%b):a;
}
signed main()
{int n;cin>>n;while(n--){int a,b;cin>>a>>b;cout<<gcd(a,b)<<endl; }return 0;
}
欧拉函数
求任意一数的欧拉函数 O(n*sqrt(a))
873. 欧拉函数 - AcWing题库

#include<bits/stdc++.h>
using namespace std;signed main()
{int n;cin>>n;while(n--){int x;cin>>x;int res=x;for(int i=2;i<=x/i;i++){if(x%i==0){res=res/i*(i-1);while(x%i==0) x/=i;} }if(x>1) res=res/x*(x-1);cout<<res<<endl;}return 0;
} 求1-n中每个数的欧拉函数 O(n)
874. 筛法求欧拉函数 - AcWing题库
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int prime[N],cnt;
bool st[N];
int phi[N];//欧拉函数typedef long long LL;
signed main()
{int n;cin>>n;phi[1]=1;for(int i=2;i<=n;i++){if(!st[i]) {prime[cnt++]=i;phi[i]=i-1;//质数的欧拉函数 }for(int j=0;prime[j]<=n/i;j++){st[prime[j]*i]=true;if(i%prime[j]==0) {phi[prime[j]*i]=prime[j]*phi[i]; //括号里质因子是一样的,只是n要多乘上一个 break;}phi[prime[j]*i]=phi[i]*(prime[j]-1); //prime是质数且i不能整除prime,则说明两数没有公因数//那么prime[j]*i比i只是多了一个质因子prime[j] }}LL res=0;for(int i=1;i<=n;i++) res+=phi[i];cout<<res;return 0;
}快速幂
快速幂
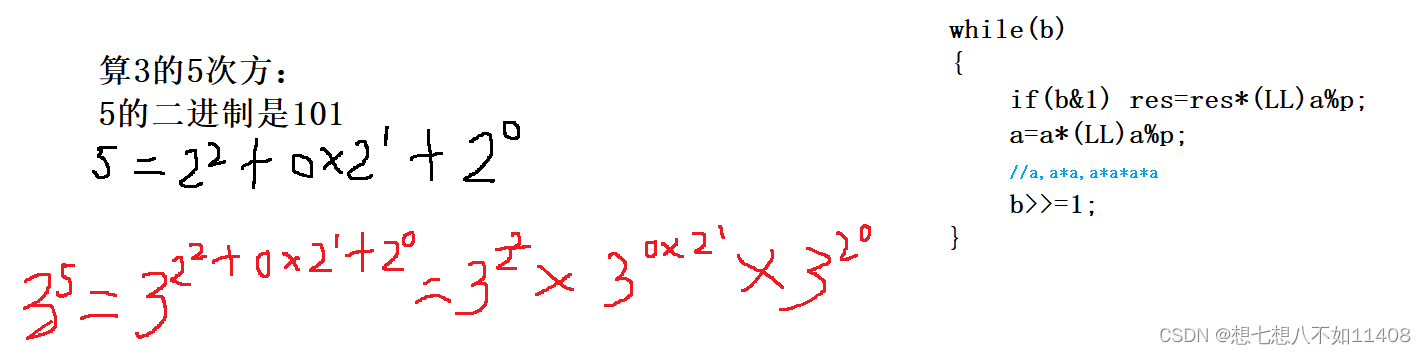
875. 快速幂 - AcWing题库
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;LL qmi(int a,int b,int p)
{LL res=1%p;while(b){if(b&1) res=res*(LL)a%p;a=a*(LL)a%p;b>>=1;}return res;
}
signed main()
{int n; cin>>n;while(n--){int a,b,p;cin>>a>>b>>p;cout<<qmi(a,b,p)<<endl; }return 0;
} 快速幂求逆元
876. 快速幂求逆元 - AcWing题库
(1)当a与p互质时,用快速幂求逆元(费马小定理):quick_power(a, b, p);
(2)当a与p不互质时,用扩展欧几里得算法求逆元:exgcd(a, p, x, y)。
概念:
 证明:费马小定理(通俗易懂) - 知乎 (zhihu.com)
证明:费马小定理(通俗易懂) - 知乎 (zhihu.com)
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;LL qmi(int a,int b,int p)
{LL res=1%p;while(b){if(b&1) res=res*(LL)a%p;a=a*(LL)a%p;b>>=1;}return res;
}
signed main()
{//当a和p不互质时无解,由于p是质数,也就只有a是p的倍数时无解 int n; cin>>n;while(n--){int a,b,p;cin>>a>>p;if(a%p==0) puts("impossible"); else cout<<qmi(a,p-2,p)<<endl; }return 0;
} 扩展欧几里得算法
扩展欧几里得算法
877. 扩展欧几里得算法 - AcWing题库
主要是递归。先正着求出gcd的值,求完之后倒着求x,y。
AcWing 877. 扩展欧几里得算法 - AcWing
#include<bits/stdc++.h>
using namespace std;int exgcd(int a,int b,int &x,int &y)
{if(b==0){x=1,y=0;return a; } int x1,y1,gcd;gcd=exgcd(b,a%b,x1,y1);x=y1,y=x1-a/b*y1;return gcd;
}signed main()
{int n;cin>>n;while(n--){int a,b,x,y;cin>>a>>b;exgcd(a,b,x,y);cout<<x<<" "<<y<<endl;}return 0;
}线性同余方程
878. 线性同余方程 - AcWing题库
想不明白主要应该是不太清楚裴属定理,看这个:裴蜀定理 - OI Wiki (oi-wiki.org)
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
int exgcd(int a,int b,int &x,int &y)
{if(b==0){x=1,y=0;return a; } int x1,y1,gcd;gcd=exgcd(b,a%b,x1,y1);x=y1,y=x1-a/b*y1;return gcd;
}signed main()
{int n;cin>>n;while(n--){int a,b,m;cin>>a>>b>>m;int x,y;int d=exgcd(a,m,x,y);if(b%d) puts("impossible");else cout<<(LL)b/d*x%m<<endl;}return 0;
}中国剩余定理
204. 表达整数的奇怪方式 - AcWing题库
基础中国剩余定理:算法学习笔记(10): 中国剩余定理 - 知乎 (zhihu.com)
好难,明天再看
高斯消元法
883. 高斯消元解线性方程组 - AcWing题库
#include<bits/stdc++.h>
using namespace std;
const int N=110;
const double eps = 1e-8;
int n;
double a[N][N];int gauss() // 高斯消元,答案存于a[i][n]中,0 <= i < n
{int c,r;//列,行for(c=0,r=0;c<n;c++)//遍历所有列 {int t=r;//最上面一个,还没确定for(int i = r ; i < n ; i ++){if( fabs(a[i][c]) > fabs(a[t][c]) ) t=i;//把最大的换上去 } if(fabs(a[t][c])<eps) continue;//如果这个最小的是0,跳过 for(int i=c;i<=n;i++) swap(a[t][i],a[r][i]);//交换 for(int i=n;i>=c;i--) a[r][i]/=a[r][c]; //首位变成1 for(int i=r+1;i<n;i++){if(fabs(a[i][c])>eps){for(int j=n;j>=c;j--){a[i][j]-=a[r][j]*a[i][c]; } }} r ++ ;}if(r<n){for(int i=r;i<n;i++)//从没走到的一行开始{if(fabs(a[i][n])>eps) return 2;//无解 }return 1; //无穷解 }//只有一解for(int i=n-1;i>=0;i--){for(int j=i+1;j<n;j++){a[i][n]-=a[i][j]*a[j][n];}} return 0;
}signed main()
{cin>>n;for(int i=0;i<n;i++){for(int j=0;j<n+1;j++){cin>>a[i][j]; }} int t=gauss();if (t == 2) puts("No solution");else if (t == 1) puts("Infinite group solutions");else{for (int i = 0; i < n; i ++ )printf("%.2lf\n", a[i][n]);}return 0;
} 从1开始存的版本。
#include<bits/stdc++.h>
using namespace std;
const int N=110;
const double eps=1e-8;
int n;
double a[N][N];int gauss()
{int r=1,c=1;//行列,r<=n,c<=n+1for(r=1,c=1;c<=n;c++) //遍历每一列 {int t=r;//记录行 for(int i=t;i<=n;i++){if(fabs(a[i][c]>fabs(a[t][c]))) t=i; }if(fabs(a[t][c])<eps) continue;//走了几列同时代表确定了几行 for(int i=c;i<=n+1;i++) swap(a[t][i],a[r][i]);for(int i=n+1;i>=c;i--) a[r][i]/=a[r][c];for(int i=r+1;i<=n;i++)//对每一行 {if(fabs(a[i][c])<eps) continue;//如果这个是0,不操作for(int j=n+1;j>=c;j--){a[i][j]-=a[r][j]*a[i][c]; } } r++;}if(r<n+1){for(int i=r;i<=n;i++){if(fabs(a[i][n+1])>eps) return 0;//无解 }return 2;//无穷解 }for(int i=n-1;i>=1;i--){for(int j=i+1;j<=n+1;j++){a[i][n+1]-=a[j][n+1]*a[i][j]; } } return 1;
}
signed main()
{cin>>n; for(int i=1;i<=n;i++){for(int j=1;j<=n+1;j++){cin>>a[i][j];}}int t=gauss();if(t==0) puts("No solution");else if(t==2) puts("Infinite group solutions");else{for(int i=1;i<=n;i++) printf("%.2lf\n",a[i][n+1]);}return 0;
}884. 高斯消元解异或线性方程组 - AcWing题库
#include<bits/stdc++.h>
using namespace std;
const int N=110;int n;
int a[N][N];void guass()
{int r,c;for(r=1,c=1;c<=n;c++)//枚举列 {int t=r;for(int i=r;i<=n;i++){if(a[i][c]){t=i;break;} }if(a[t][c]==0) continue;//说明第c列都是0 for(int i=c;i<=n+1;i++) swap(a[r][i],a[t][i]);for(int i=r+1;i<=n;i++){if(a[i][c]==0) continue;for(int j=c;j<=n+1;j++){a[i][j]^=a[r][j]; } } r++;}if(r<n+1)//说明等式左边都是0,判断等式右边即可 {for(int i=r;i<=n;i++){if(a[i][n+1]!=0)//无解 {puts("No solution");return; }} puts("Multiple sets of solutions");return;}//输出结果for(int i=n-1;i>=1;i--){for(int j=i+1;j<=n+1;j++){a[i][n+1]^=a[i][j]*a[j][n+1]; } } for(int i=1;i<=n;i++){cout<<a[i][n+1]<<endl;}
}
signed main()
{cin>>n; for(int i=1;i<=n;i++){for(int j=1;j<=n+1;j++){cin>>a[i][j];}}guass(); return 0;
}求组合数
885. 求组合数 I - AcWing题库
1<=b<=a<=2000
#include<bits/stdc++.h>
using namespace std;
const int N=2010,mod=1e9+7;
int a[N][N];void init()
{for(int i=0;i<N;i++){for(int j=0;j<=i;j++){if(j==0) a[i][j]=1;else a[i][j]=(a[i-1][j]+a[i-1][j-1])%mod;}}
}
signed main()
{init();int n;cin>>n;while(n--){int c,b;cin>>c>>b;cout<<a[c][b]<<endl;}return 0;
}886. 求组合数 II - AcWing题库
1<=b<=a<=1e5
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e5+10,mod=1e9+7;int fact[N],infact[N];
int qmi(int a,int k,int p)
{int res=1;while(k){if(k&1) res=(LL)res*a%p;a=(LL)a*a%p;k>>=1;}return res;
}
signed main()
{fact[0]=infact[0]=1;for(int i=1;i<N;i++){fact[i]=(LL)fact[i-1]*i%mod;infact[i]=(LL)infact[i-1]*qmi(i,mod-2,mod)%mod; }int n; cin>>n;while(n--){int a,b;cin>>a>>b;cout<<(LL)fact[a]*infact[b]%mod*infact[a-b]%mod<<endl;}return 0;
}相关文章:

【算法基础】数学知识
质数 质数的判定 866. 试除法判定质数 - AcWing题库 时间复杂度是logN #include<bits/stdc.h> using namespace std; int n; bool isprime(int x) {if(x<2) return false;for(int i2;i<x/i;i){if(x%i0) return false;}return true; } signed main() {cin>&g…...
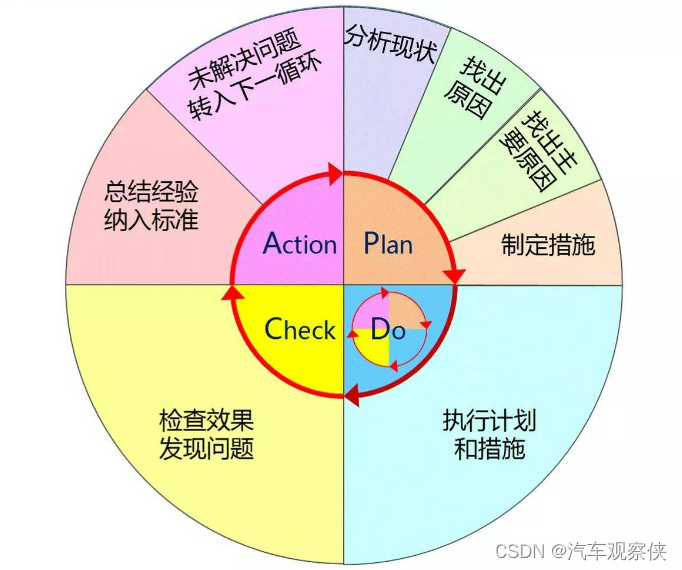
PDCA循环
目录 1.认识PDCA: 2.PDCA循环的经典案例 3.PDCA的四个阶段和八个步骤 4.PDCA循环的优缺点: 5.案例 6.其他作用 1.认识PDCA: PDCA循环最早由美国质量统计控制之父Shewhat(休哈特)提出的PDS(Plan Do Se…...
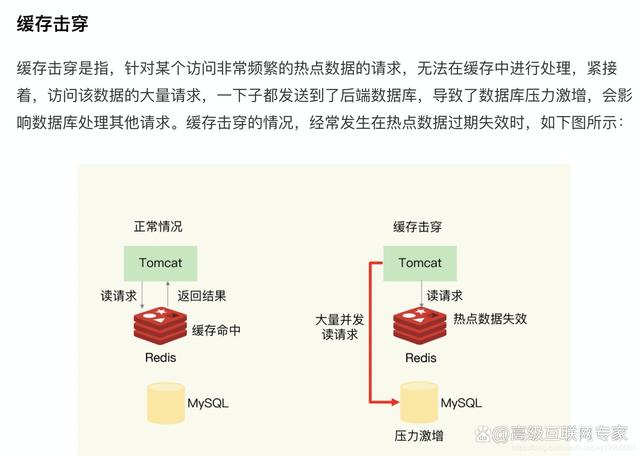
Redis 缓存雪崩、缓存穿透、缓存击穿
Redis 是一种常用的内存缓存工具,但在某些情况下,它可能会遭受缓存雪崩、缓存穿透和缓存击穿等问题。下面是一些预防这些问题的建议: 1、缓存雪崩 缓存雪崩指的是在某个时间点上,大量的缓存数据同时失效或过期,导致大…...
Android Media3 ExoPlayer 开启缓存功能
ExoPlayer 开启播放缓存功能,在下次加载已经播放过的网络资源的时候,可以直接从本地缓存加载,实现为用户节省流量和提升加载效率的作用。 方法一:采用 ExoPlayer 缓存策略 第 1 步:实现 Exoplayer 参考 Exoplayer 官…...

MyBatis注解开发
MyBatis常用注解 注解对应XML说明Insert< insert>新增SQLUpdate< update>更新SQLDelete< delete>删除SQLSelect< select>查询SQLParam–参数映射Results< resultMap>结果映射Result< id>< result>字段映射 开发流程: 1…...
C# Onnx Yolov8 Cls 分类
效果 项目 代码 using Microsoft.ML.OnnxRuntime; using Microsoft.ML.OnnxRuntime.Tensors; using OpenCvSharp; using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System…...

Fiddler常用的快键键
Fiddler有很多常用的快捷键,这些快捷键可以帮助你更快速地完成任务。以下是一些常用的快捷键: F12:启动/停止抓包。 CtrlR:打开FiddlerScript窗口。 CtrlH:切换到 Inspector 页签的 Header 视图。 CtrlT:切…...

【Linux】生产消费模型 + 线程池
文章目录 📖 前言1. 生产消费模型2. 阻塞队列2.1 成员变量:2.2 入队(push)和出队(pop):2.3 封装与测试运行:2.3 - 1 对代码进一步封装2.3 - 2 分配运算任务2.3 - 3 测试与运行 3. 循环阻塞队列3.1 POSIX信号量:3.1 - 1…...
基于springboot+vue的爱心助农网站(前后端分离)
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…...
)
“华为杯”研究生数学建模竞赛2019年-【华为杯】D题:汽车行驶工况构建(附获奖论文和MATLAB代码实现)
目录 摘 要: 1. 问题重述 2. 模型假设 2.1 题目对模型给出的假设...

v-cloak的作用和原理
1、作用 v-cloak 指令常用在插值表达式的标签中,用于解决当网络加载很慢或者频繁渲染页面时,页面显示出源代码的情况。 所以为了提高用户的体验性,使用指令 v-cloak,搭配着 CSS 一起使用,在加载时隐藏挂载内容&#x…...

pip pip3安装库时都指向python2的库
当在python3的环境下使用pip3安装库时,发现居然都指向了python2的库 pip -V pip3 -V安装命令更改为: python3 -m pip install <package>...

和逸云 RK3229 如何进入maskrom强刷模式
图中红圈两个点短接以后插usb,就可以进入maskrom模式强刷...

防静电离子风扇的应用及优点
防静电静电离子风扇是一种用于消除静电的设备,它可以通过离子化原理将静电荷离子化,从而达到静电的效果。防静电静电离子风扇通常采用离子风扇的形式,通过离子化原理将静电荷离子化,从而消除静电。 防静电静电离子风扇的工作原理…...
git中无法使用方向键的问题
windows下使用git命令行执行react脚本安装,发现无法使用上下键来去选中选项。最后只能换成cmd命令执行,发现可以上下移动以选中需要的选项。 bash命令行:移动光标无法移动选项 cmd命令行...

负载均衡中间件---Nginx
一.nginx的好处 学习 Nginx 对于一个全栈开发者来说是非常有价值的,下面是一些学习 Nginx 的原因和好处: 反向代理和负载均衡:Nginx 是一个高性能的反向代理服务器,可以用于将客户端请求转发给多个后端服务器,实现负…...

Linux硬链接、软链接
硬链接是一个目录条目(在基于目录的文件系统中),它将一个名称与一个文件关联起来。因此,每个文件必须至少有一个硬链接。为文件创建额外的硬链接可以使该文件的内容可以通过额外的路径访问(即通过不同的名称或在不同的目录中)这会导致别名效应(alias eff…...
)
React面试题总结(一)
1、redux本来是同步的,为什么它能执行异步代码?实现原理是什么?中间件的实现原理是什么? 1、Redux-thunk这个中间件支持异步操作 2、执行异步的操作首先需要下载一个thunk,通过thunk来进行异步的一个操作,支…...
一句话设计模式12:适配器模式
适配器模式: 继承原对象,持有目标对象; 文章目录 适配器模式: 继承原对象,持有目标对象;前言一、适配器模式的作用二、如何适配器模式直接上代码 总结 前言 适配器模式一般使用场景是: 将一个类(接口)转换成客户希望的另外一个类(接口)。其中适配器充当一个假的原类的作用; 一…...
iOS加固保护技术:保护你的iOS应用免受恶意篡改
目录 转载:开始使用ipaguard 前言 下载ipa代码混淆保护工具 获取ipaguard登录码 代码混淆 文件混淆 IPA重签名与安装测试 转载:开始使用ipaguard 前言 iOS加固保护是直接针对ios ipa二进制文件的保护技术,可以对iOS APP中的可执行文件…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...
