二叉搜索树(BST,Binary Search Tree)
文章目录
- 1. 二叉搜索树
- 1.1 二叉搜索树概念
- 1.2 二叉搜索树的查找
- 1.3 二叉搜索树的插入
- 1.4 二叉搜索树的删除
- 2 二叉搜索树的实现
- 3 二叉搜索树的应用
- 3.1二叉搜索树的性能分析
1. 二叉搜索树
1.1 二叉搜索树概念
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值。
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值。
- 它的左右子树也分别为二叉搜索树。
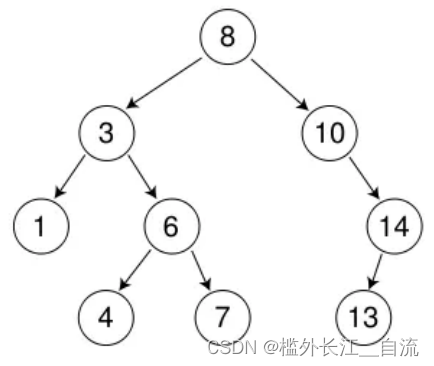
1.2 二叉搜索树的查找
a、从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找。
b、最多查找高度次(最高位O(N)),走到到空,还没找到,这个值不存在。
1.3 二叉搜索树的插入
插入的具体过程如下:
a. 树为空,则直接新增节点,赋值给root指针
b. 树不空,按二叉搜索树性质查找插入位置,插入新节点
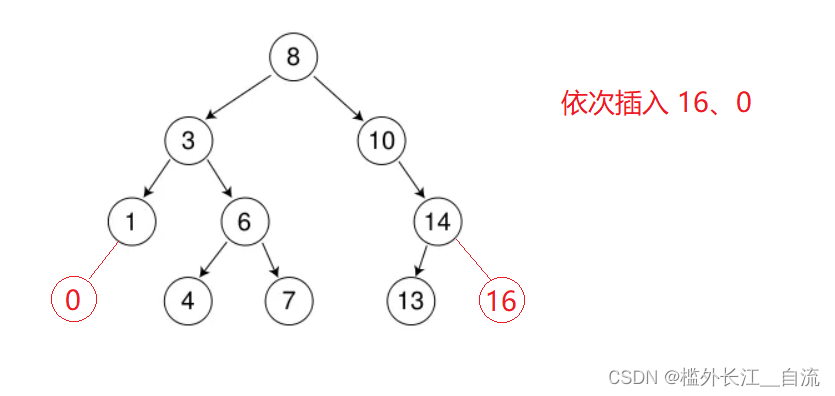
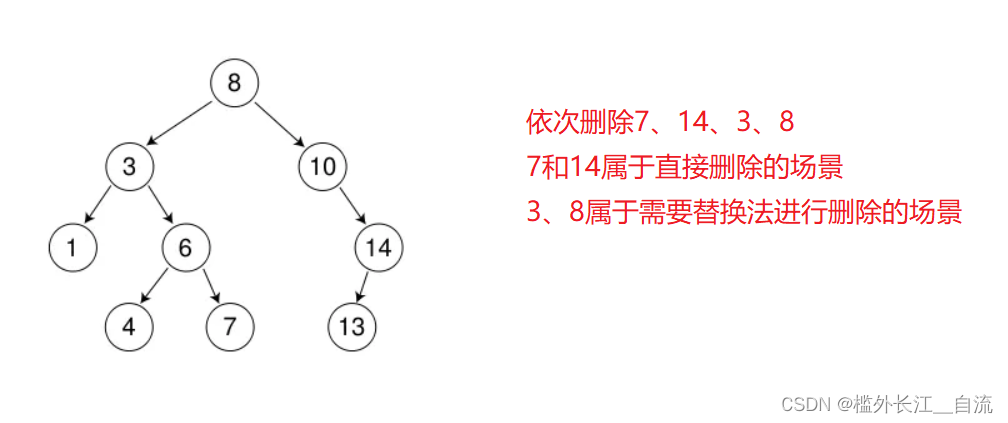
1.4 二叉搜索树的删除
首先查找元素是否在二叉搜索树中,如果不存在,则返回, 否则要删除的结点可能分下面四种情
况:
a. 要删除的结点无孩子结点
b. 要删除的结点只有左孩子结点
c. 要删除的结点只有右孩子结点
d. 要删除的结点有左、右孩子结点
看起来有待删除节点有4中情况,实际情况a可以与情况b或者c合并起来,因此真正的删除过程
如下:
情况b:删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点–直接删除
情况c:删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点–直接删除
情况d:在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删除节点
中,再来处理该结点的删除问题–替换法删除。
2 二叉搜索树的实现
template<class K>
struct BSTreeNode
{BSTreeNode* _left;BSTreeNode* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}
};
template<class K>
struct BSTree
{typedef BSTreeNode<K> Node;
public:BSTree():_root(nullptr){}bool insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}elsereturn false;}cur = new Node(key);if (parent->_key < key){parent->_right = cur;}elseparent->_left = cur;return true;}bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key > key)cur = cur->_left;else if (cur->_key < key)cur = cur->_right;elsereturn true;}return false;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else//找到了{if (cur->_left == nullptr)//左为空{if (cur == _root){_root = _root->_right;}else{if (parent->_right == cur){parent->_right = cur->_right;}else{parent->_left = cur->_right;}}}else if (cur->_right == nullptr)//右为空{if (cur == _root){_root = _root->_left;}else{if (parent->_right = cur){parent->_right = cur->_left;}else{parent->_left = cur->_left;}}}else//左右都不为空{Node* parent = cur;Node* LeftMax = cur->_left;while (LeftMax->_right){parent = LeftMax;LeftMax = LeftMax->_right;}swap(cur->_key, LeftMax->_key);if (parent->_left == LeftMax){parent->_left = LeftMax->_left;}else{parent->_right = LeftMax->_left;}cur = LeftMax;}delete cur;return true;}}return false;}void InOrder(){_InOrder(_root);cout << endl;}void _InOrder(Node* root){if (root == NULL){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}
private:Node* _root;
};void TestBSTree1()
{int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };BSTree<int> t;for (auto e : a){t.insert(e);}t.InOrder();t.Erase(4);t.InOrder();t.Erase(6);t.InOrder();t.Erase(7);t.InOrder();t.Erase(3);t.InOrder();for (auto e : a){t.Erase(e);}t.InOrder();
}
3 二叉搜索树的应用
- K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到
的值。
比如:给一个单词word,判断该单词是否拼写正确,具体方式如下:
以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树
在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。 - KV模型:每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。该种方
式在现实生活中非常常见:
比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英
文单词与其对应的中文<word, chinese>就构成一种键值对;
再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出
现次数就是<word, count>就构成一种键值对。
以下是完整的代码,包括改造二叉搜索树为KV结构、测试二叉搜索树的函数和主函数:cpp
#include <iostream>
#include <string> using namespace std; template<class K, class V>
struct BSTNode
{ BSTNode(const K& key = K(), const V& value = V()) : _pLeft(nullptr) , _pRight(nullptr), _key(key), _value(value) {} BSTNode<K, V>* _pLeft; BSTNode<K, V>* _pRight; K _key; V _value;
}; template<class K, class V>
class BSTree
{
public: typedef BSTNode<K, V> Node; typedef Node* PNode;
public: BSTree(): _pRoot(nullptr){} PNode Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return true;}}return false;}bool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else // 找到了{// 左为空if (cur->_left == nullptr){if (cur == _root){_root = cur->_right;}else{if (parent->_right == cur){parent->_right = cur->_right;}else{parent->_left = cur->_right;}}}// 右为空else if (cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else{if (parent->_right == cur){parent->_right = cur->_left;}else{parent->_left = cur->_left;}}} // 左右都不为空 else{// 找替代节点Node* parent = cur;Node* leftMax = cur->_left;while (leftMax->_right){parent = leftMax;leftMax = leftMax->_right;}swap(cur->_key, leftMax->_key);if (parent->_left == leftMax){parent->_left = leftMax->_left;}else{parent->_right = leftMax->_left;}cur = leftMax;}delete cur;return true;}}return false;}
private: PNode _pRoot;
}; 3.1二叉搜索树的性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二
叉搜索树的深度的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
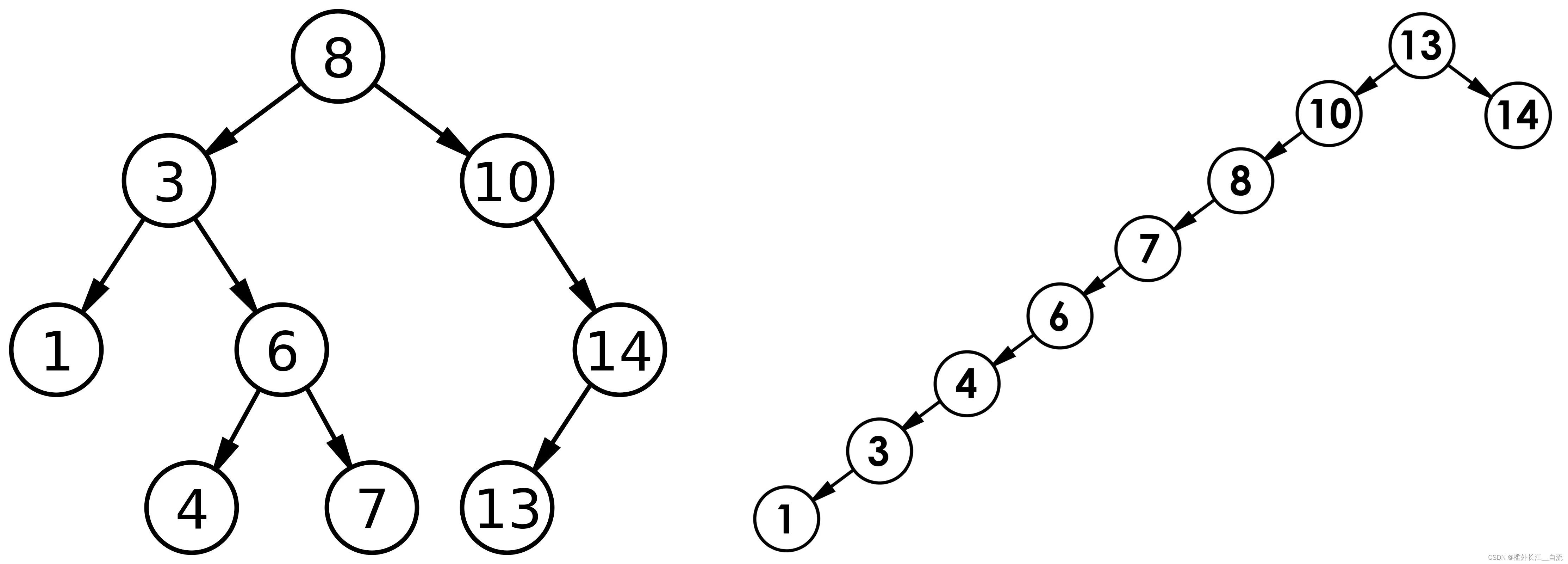
最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为: l o g 2 N log_2 N log2N
最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为: N 2 \frac{N}{2} 2N
问题:如果退化成单支树,二叉搜索树的性能就失去了。那能否进行改进,不论按照什么次序插
入关键码,二叉搜索树的性能都能达到最优?AVL树和红黑树就可以上场了。
相关文章:

二叉搜索树(BST,Binary Search Tree)
文章目录 1. 二叉搜索树1.1 二叉搜索树概念1.2 二叉搜索树的查找1.3 二叉搜索树的插入1.4 二叉搜索树的删除 2 二叉搜索树的实现3 二叉搜索树的应用3.1二叉搜索树的性能分析 1. 二叉搜索树 1.1 二叉搜索树概念 二叉搜索树又称二叉排序树,它或者是一棵空树…...
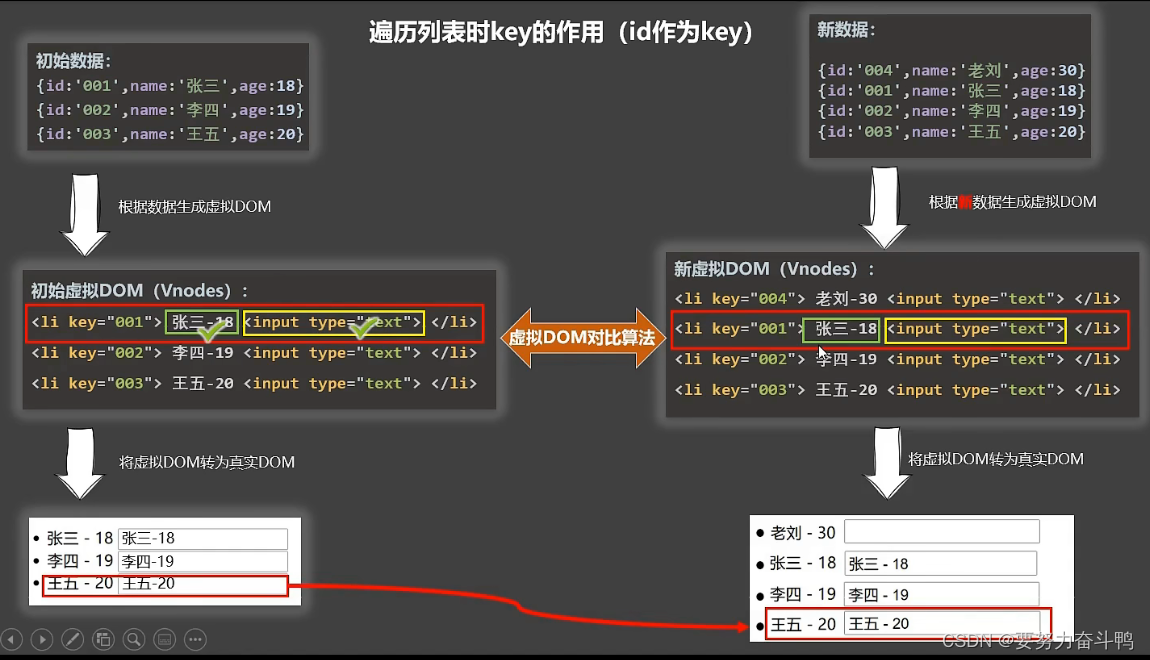
分析key原理
总结: key是虚拟dom对象的标识,当数据发生变化时,vue会根据新数据生成新的虚拟dom,随后vue进行新虚拟dom与旧虚拟dom的差异比较 比较规则: ①旧虚拟dom中找到了与新虚拟dom相同的key 若虚拟dom中的内容没变,…...
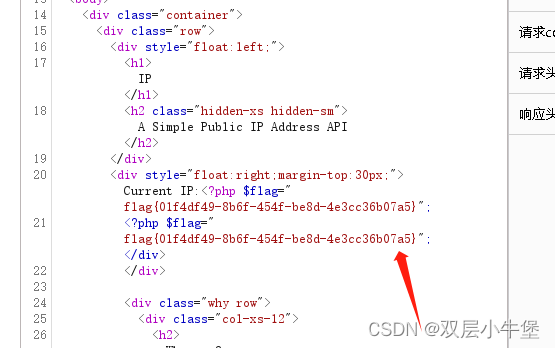
[CISCN2019 华东南赛区]Web11 SSTI
这道SSTI 差点给我渗透的感觉了 全是API 我还想去访问API看看 发现这里读取了我们的ip 我们抓包看看是如何做到的 没有东西 我们看看还有什么提示 欸 那我们可不可以直接修改参数呢 我们传递看看 发现成功了 是受控的 这里我就开始没有思路了 于是看了wp 说是ssti 那我们看…...

百度春招C++后端面经总结
这次的面经,主要都是问操作系统、网络编程、C++ 这三大方向。 能明显感觉到,C++面试和Java或者Go面试重点,Java/Go主要是问MySQL、Redis。 一、介绍一下webserver项目 服务器开始运行,创建(初始化)线程池(IO密集型,线程数n+1); 创建 epoll 对连接进行监听 监听到连…...

小程序开发一个多少钱啊
在今天的数字化时代,小程序已经成为一种非常流行的应用程序形式。由于它们的便捷性、易用性和多功能性,小程序吸引了越来越多的用户和企业。但是,很多人在考虑开发一个小程序时,都会遇到同一个问题:开发一个小程序需要…...
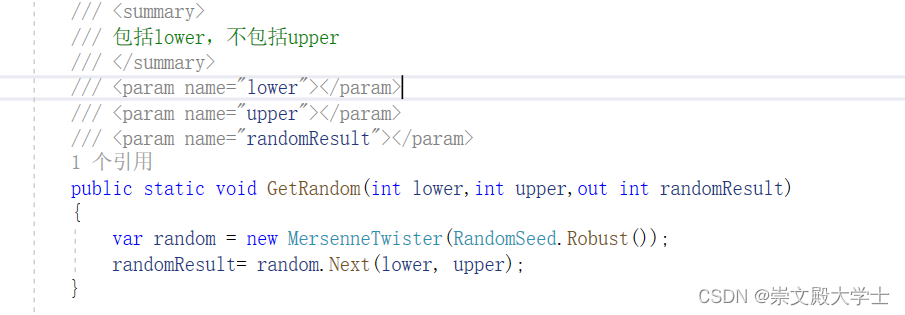
C# 随机数生成 Mersenne Twister 马特赛特旋转演算法 梅森旋转算法
NuGet安装MathNet.Numerics 引用: using MathNet.Numerics.Random; /// <summary>/// 包括lower,不包括upper/// </summary>/// <param name"lower"></param>/// <param name"upper"></param>/// <para…...
)
C++进阶(二)
目录 1、Vector2D 默认构造、重载 2、char 深度理解 3、深度理解简单的类操作 1、Vector2D 默认构造、重载 #include <iostream> #include <cmath>class Vector2D { private:double x; // X坐标double y; // Y坐标public:// 默认构造函数,将向量初…...

zoneinfo
在Linux系统中,zoneinfo是一个包含了世界各地时区信息的目录,通常位于/usr/share/zoneinfo。这个目录下的子目录和文件名对应了各个时区的名称。例如,/usr/share/zoneinfo/America/Los_Angeles文件就包含了美国洛杉矶的时区信息。 你可以通过…...
基于微信小程序的实验室预约管理系统设计与实现
前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java、小程序技术领域和毕业项目实战✌💗 👇🏻…...
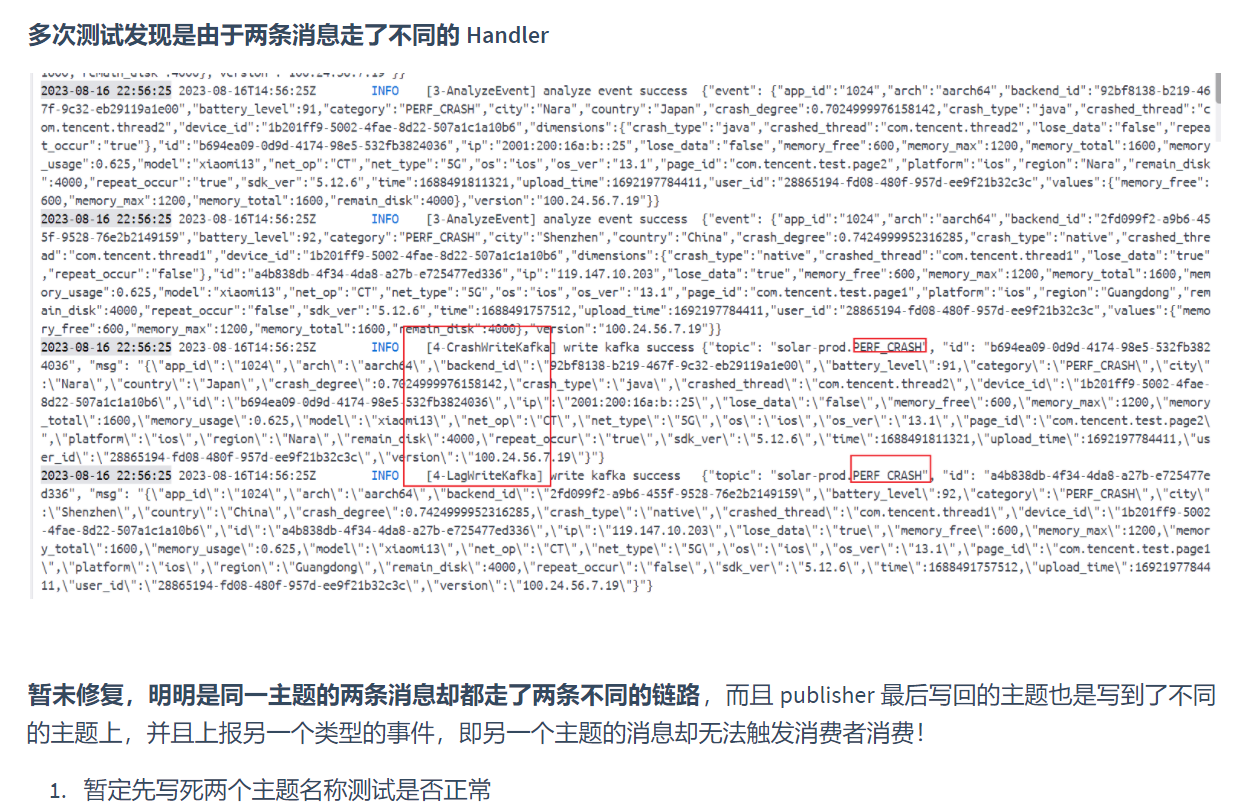
腾讯mini项目-【指标监控服务重构】2023-08-17
今日已办 定位昨日发现的问题 来回测试发现依然出现该问题 将 pub/sub 的库替换为原来官方基于 sarama 的实现,发现问题解决了,所以问题的根本是 kafkago 这个库本身存在问题 依据官方的实现,尝试自定义实现 pub/sub sarama 与 kafka-go …...
前端需要知道的计算机网络知识----网络安全,自学网络安全,学习路线图必不可少,【282G】初级网络安全学习资源分享!
网络安全(英语:network security)包含网络设备安全、网络信息安全、网络软件安全。 黑客通过基于网络的入侵来达到窃取敏感信息的目的,也有人以基于网络的攻击见长,被人收买通过网络来攻击商业竞争对手企业࿰…...
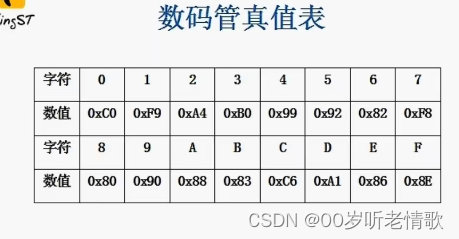
#循循渐进学51单片机#定时器与数码管#not.4
1、熟练掌握单片机定时器的原理和应用方法。 1)时钟周期:单片机时序中的最小单位,具体计算的方法就是时钟源分之一。 2)机器周期:我们的单片机完成一个操作的最短时间。 3)定时器:打开定时器“储存寄存器…...

基于Android+OpenCV+CNN+Keras的智能手语数字实时翻译——深度学习算法应用(含Python、ipynb工程源码)+数据集(五)
目录 前言总体设计系统整体结构图系统流程图 运行环境模块实现1. 数据预处理2. 数据增强3. 模型构建4. 模型训练及保存5. 模型评估6. 模型测试 系统测试1. 训练准确率2. 测试效果3. 模型应用1)程序下载运行2)应用使用说明3)测试结果 相关其它…...
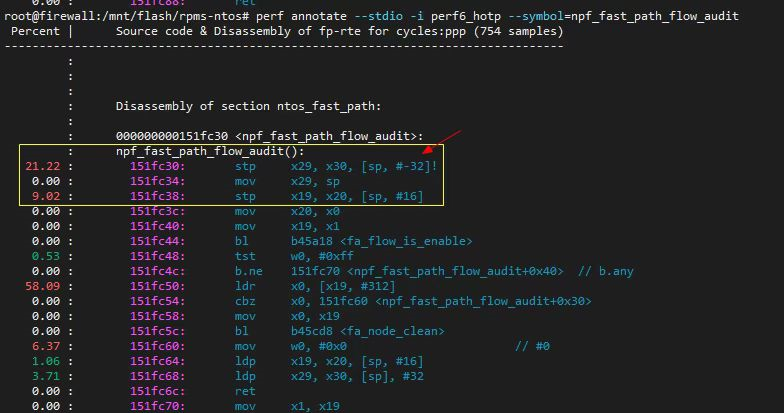
Linux: Cache 简介
文章目录 1. 前言2. 背景3. Cache 硬件基础3.1 什么是 Cache ?3.2 Cache 工作原理3.3 Cache 层级架构3.4 内存架构中各级访问速度概览3.5 Cache 分类3.6 Cache 的 查找 和 组织方式3.6.1 Cache 组织相关术语3.6.2 Cache 查找3.6.2.1 Cache 查找过程概述3.6.2.2 Cach…...

常见位运算公式使用场景
判断奇偶性:数值 x 为偶数当且仅当 (x & 1) 0。数值 x 为奇数当且仅当 (x & 1) 1。 交换两个数:使用异或操作符 ^ 进行交换。假设有变量 a 和 b,则可以使用以下公式交换它们的值: a a ^ b; b a ^ b; a a ^ b;取绝…...
virtualbox配置ubuntu1804虚拟机相关流程
virtualbox配置ubuntu1804虚拟机相关流程 相关版本能解决的问题安装流程1:新建虚拟机安装流程2:配置虚拟机安装流程3:安装虚拟机系统安装流程4:设置ubuntu 相关版本 virtualbox使用VirtualBox官网下载的6.1.34 r150636 版。ubunt…...
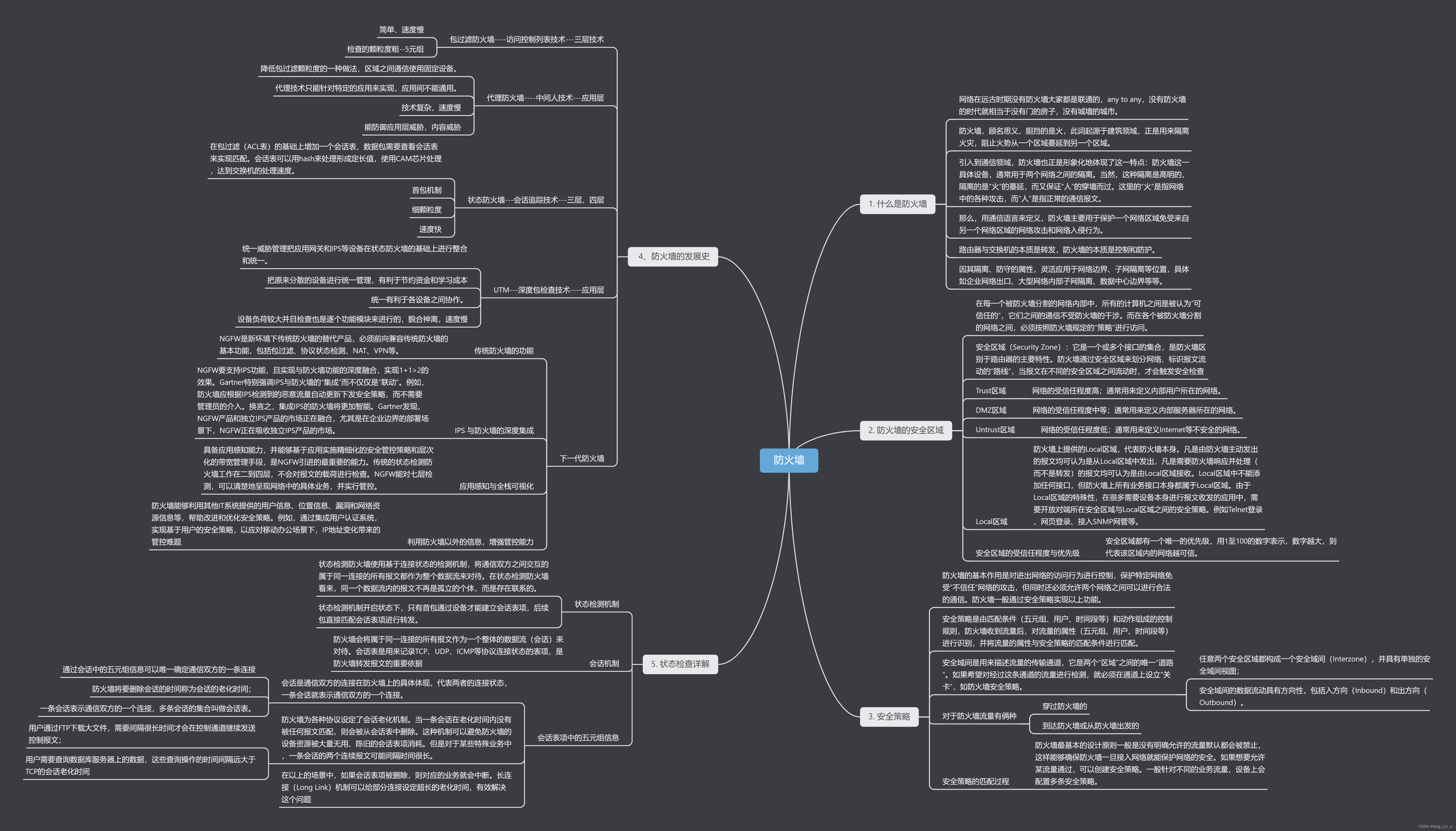
防火墙基本概念
思维导图 1. 什么是防火墙? 网络在远古时期没有防火墙大家都是联通的,any to any,没有防火墙的时代就相当于没有门的房子, 没有城墙的城市。 路由器与交换机的本质是转发,防火墙的本质是控制和防护。 防火墙ÿ…...

易点易动固定资产管理平台:打通BMP,实现高效流程管理与全生命周期管理
在现代企业管理中,固定资产的流程管理和全生命周期管理是提高效率和降低成本的关键。易点易动固定资产管理平台通过打通BMP(Business Process Management)系统,实现了固定资产流程管理和全生命周期高效化管理的目标。本文将详细介…...

uniapp webview实现双向通信
需求:uniapp webview嵌套一个h5 实现双向通信 uniapp 代码 <template><view><web-view src"http://192.168.3.150:9003/" message"onMessage"></web-view></view> </template><script>export defau…...
Linux动态库
定义:动态函数库,是在程序执行时动态(临时)由目标程序去调用 优点: 调用时不复制,程序运行时动态加载到内存,供程序调用,系统只加载一次,多个程序可以共用,…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...
