当前位置： 首页 > news >正文

Linux——vi编辑器

news 2026/2/1 20:49:34

目录

一、基本简介

二、命令模式下的常用按键

1、光标跳转按键

2、复制、粘贴、删除

三、编辑模式

四、末行模式

1、查找关键字并替换

2、保存退出

3、其他操作

五、模式切换

一、基本简介

1、最早可追随到1991年，全称为“Vi IMproved”

2、模式

        ——命令模式

        ——末行模式

        ——编辑模式

3、使用vi/vim命令编辑文件

        ——在每次运行vim编辑器时，默认进入命令模式

        格式：vim 文件

二、命令模式下的常用按键

1、光标跳转按键

功能按键
光标按单个字符移动↑、↓、←、→
光标按照单词向后跳转w
光标按照单词向前跳转b
光标跳转至行首^
光标跳转至行尾$
文档首行第一个字符gg
文档最后一行第一个字符G
跳转至指定行行号gg 或者 行号G

2、复制、粘贴、删除

功能按键
删除光标所在行dd
删除从光标处开始的n行ndd
删除光标前至行首字符d^
删除光标及之后的所有字符d$
复制光标所在行yy
复制从光标处开始的n行nyy
将缓冲区的内容粘贴到光标所在行的下一行p
将缓冲区的内容粘贴到光标所在行的上一行P
撤销操作u

三、编辑模式

功能按键
在光标前插入i
在光标所在行行首第一个非空字符前插入I
在光标后插入a
在光标所在行末尾插入A
在光标所在行上一行插入O
在光标所在行下一行插入o
删除光标所在字符并进入插入模式s
删除当前行并进入插入模式S

四、末行模式

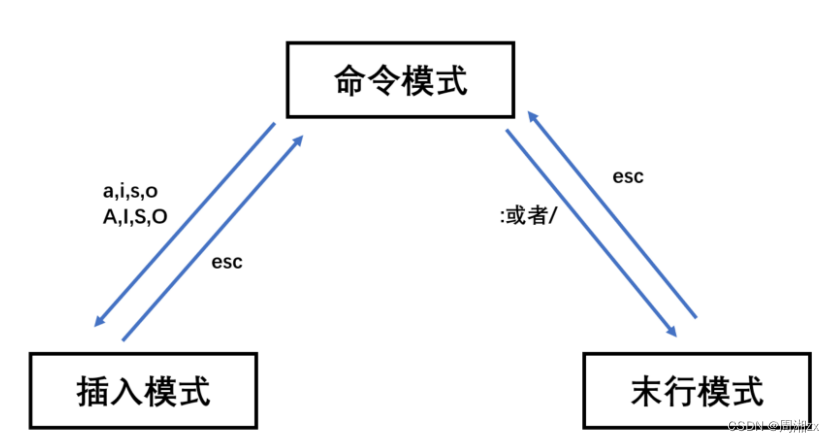
——按：或者 / 可从命令模式切换到末行模式

——按esc键可从末行模式切换到命令模式

1、查找关键字并替换

功能按键
从上而下在文件中查找字符串“word”（可按n键定位到下一个匹配的被查找 字符串）/word
将当前行中查找到的第一个字符“old”替换为“new”:s /old/new
将当前行中查找到的所有字符“old”替换为“new”:s /old/new/g
在行号“n1,n2”范围内替换所有的字符串“old”为“new”:n1,n2 s/old/new/g
将整个文件内的字符串“old”替换为“new”:% s/old/new/g

2、保存退出

功能按键
退出vi/vim编辑器，未对文件做任何编译操作才可退出:q
不保存文档内容，强制退出vi/vim编辑器:q!
保存文件:w
将文件另存为/dir/file:w /dir/file
保存文件内容并退出vi/vim编辑器:wq 或者 zz
强制保存并退出:wq!

3、其他操作

功能按键
在当前文件中读入其他文件内容:r /dir/file
查找含有“word”的行并删除:g/word/d
显示行号:set nu
关闭行号显示:set nonu
删除n1-n2行内容:n1,n2 d
复制n1-n2行到第n行后面:n1,n2 co n

五、模式切换

相关文章：

Linux——vi编辑器

目录 一、基本简介 二、命令模式下的常用按键 1、光标跳转按键 2、复制、粘贴、删除 三、编辑模式 四、末行模式 1、查找关键字并替换 2、保存退出 3、其他操作 五、模式切换 一、基本简介 1、最早可追随到1991年，全称为“Vi IMproved” 2、模式 ——命…...

编程日记 2023/9/21 19:18:03

【Linux学习笔记】权限

1. 普通用户和root用户权限之间的切换2. 权限的三个w2.1. 什么是权限（what）2.1.1. 用户角色2.1.2. 文件属性 2.2. 怎么操作权限呢？（how）2.2.1. ugo-rwx方案2.2.2. 八进制方案2.2.3. 文件权限的初始模样2.2.4. 进入一个…...

编程日记 2023/9/21 19:16:02

Aspose转pdf乱码问题

一、问题描述 ​ 在centos服务器使用aspose.word转换word文件为pdf的时候显示中文乱码(如图)，但是在win服务器上使用可以正常转换 二、问题原因 由于linux服务器缺少对应的字库导致文件转换出现乱码的 三、解决方式 1.将window中字体(c:\windows\fonts)放到linux…...

编程日记 2023/9/21 19:15:01

table中的td内部的元素不能与td等高的问题

解决该问题的办法: td标签内部的元素使用table布局&#xff0c;但是需要注意的是td必须设置高度&#xff0c;高度为任意值都可以&#xff0c;虽然设置了高度&#xff0c;但是td依然会被内部内容的高度撑开 <template><table><tr><td><div class&q…...

编程日记 2023/9/21 19:11:58

Layui + Flask | 实现数据表格修改（案例篇）（09）

此案例内容比较多，建议滑到最后点击阅读原文，阅读体验更佳。后续也会录制案例视频，将在本周内上传到同名的 b 站账号。 接下来演示用 flask + layui 搭建一个学员信息管理的案例 这个案例将会利用 flask 做后端，layui table 组件做前端，基于 restful api 完成一个学员信息…...

编程日记 2023/9/21 19:10:57

BCC源码编译和安装

接前一篇文章&#xff1a;BCC源码下载 1. 进入源码根目录 进入到BCC源码根目录。命令及结果如下&#xff1a; $ cd bcc ~/eBPF/BCC/bcc$ ls cmake CONTRIBUTING-SCRIPTS.md docs images libbpf-tools man scripts src CMakeLists.txt …...

编程日记 2023/9/21 19:09:57

linux上gitlab备份与还原

三 Gitlab备份 1.gitlab安装 1.1 添加镜像地址 添加镜像地址的目的是为了提高国内用户软件下载的速度&#xff0c;编辑(新建)文件gitlab-ce.repo&#xff0c;指令&#xff1a; vi /etc/yum.repos.d/gitlab-ce.repo复制 输入&#xff1a; [gitlab-ce] namegitlab-ce # 清华…...

编程日记 2023/9/21 19:07:55

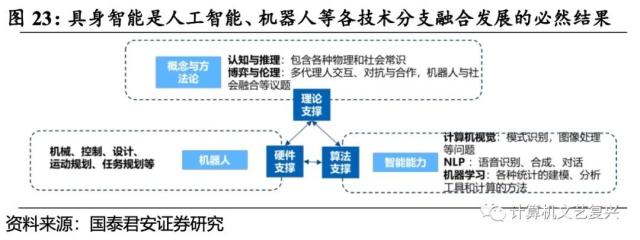
【精华】具身智能：人工智能的下一个浪潮

从符号主义到联结主义&#xff0c;智能体与真实世界的交互得到日益重视。上世纪五十年代的达特茅斯会议之后的一段时期内&#xff0c;对人工智能的研究主要限于符号处理范式&#xff08;符号主义&#xff09;。符号主义的局限性很快在实际应用中暴露出来&#xff0c;并催动了联…...

编程日记 2023/9/21 19:04:52

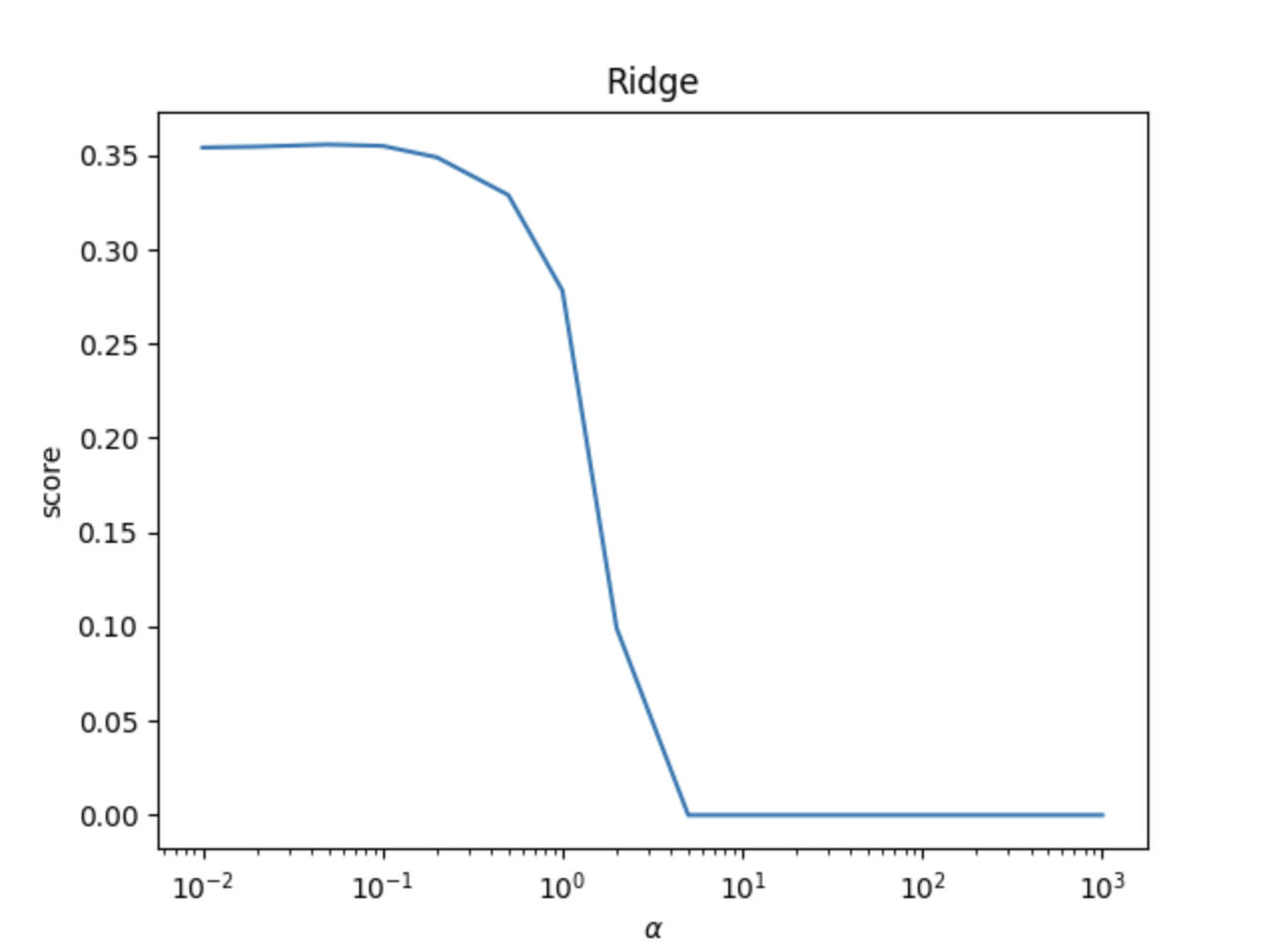
【线性回归、岭回归、Lasso回归分别预测患者糖尿病病情】数据挖掘实验一

Ⅰ、项目任务要求 任务描述&#xff1a;将“diabetes”糖尿病患者数据集划分为训练集和测试集&#xff0c;利用训练集分别结合线性回归、岭回归、Lasso回归建立预测模型&#xff0c;再利用测试集来预测糖尿病患者病情并验证预测模型的拟合能力。具体任务要求如下&#xff1a; …...

编程日记 2023/9/21 19:02:50

037：vue项目监听页面变化，动态设置iframe元素高度

第037个 查看专栏目录: VUE ------ element UI 专栏目标 在vue和element UI联合技术栈的操控下&#xff0c;本专栏提供行之有效的源代码示例和信息点介绍&#xff0c;做到灵活运用。 &#xff08;1&#xff09;提供vue2的一些基本操作&#xff1a;安装、引用&#xff0c;模板使…...

编程日记 2023/9/21 19:01:49

探索前端生成二维码技术：简单实用的实现方式

引言 随着智能手机的普及&#xff0c;二维码已经成为了现代生活中不可或缺的一部分。在许多场景下&#xff0c;我们都需要将某些信息或链接以二维码的形式展示出来。本文将介绍一种简单实用的前端生成二维码的技术&#xff0c;并给出具体的代码示例。 二维码生成原理 首先&a…...

编程日记 2023/9/21 19:00:48

python装13的一些写法

一些当你离职后&#xff0c;让老板觉拍大腿的代码 1. any(** in ** for ** in **) 判断某个集合元素&#xff0c;是否包含某个/某些元素 代码&#xff1a; if __name__ __main__:# 判断 list1 中是否包含某个/某些元素list1 [1,2,3,4]a any(x in [5,4] for x in list1) 输…...

编程日记 2023/9/21 18:59:47

黑马JVM总结（十八）

&#xff08;1&#xff09;G1_FullGC的概念辨析 SerialGC&#xff1a;串行的&#xff0c;ParallelGC&#xff1a;并行的 &#xff0c;CMS和G1都是并发的 这几种垃圾回收器的新生代回收机制时相同的&#xff0c;SerialGC和ParalledGC&#xff1a;老年代内存不足触发的叫FullGC…...

编程日记 2023/9/21 18:58:46

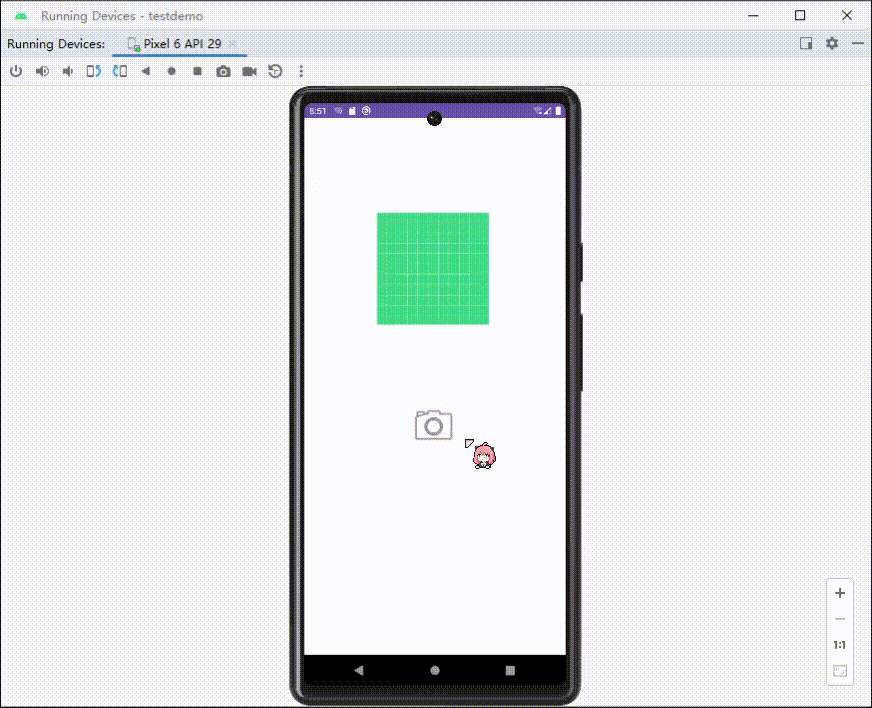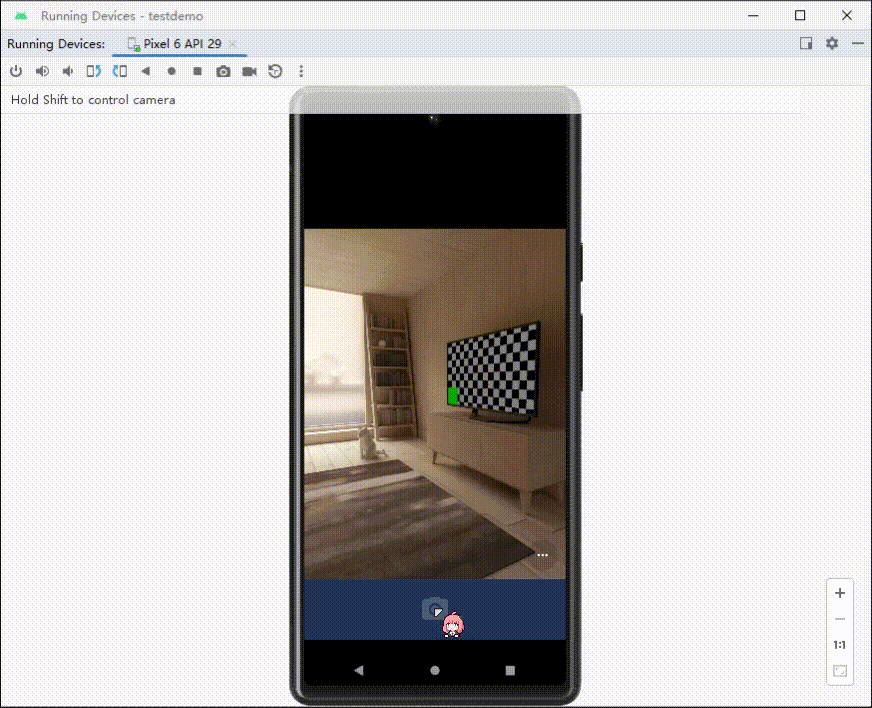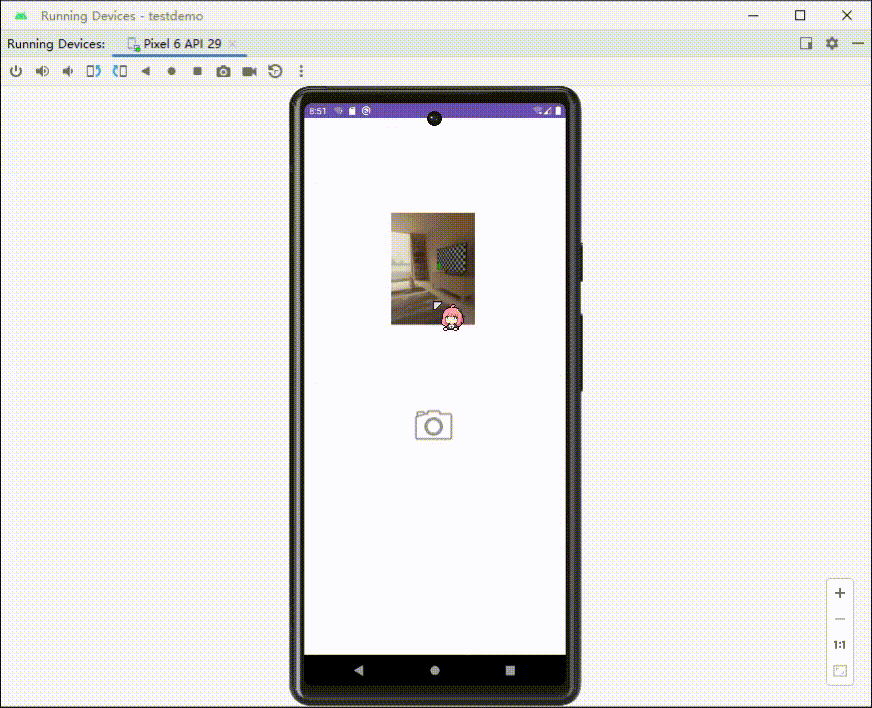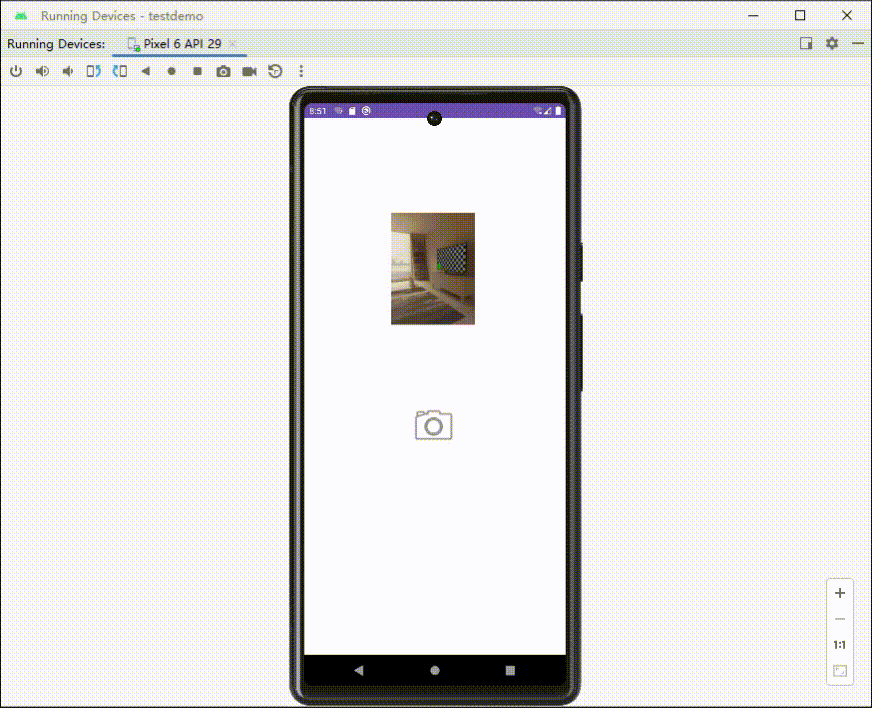
Android调用相机拍照，展示拍摄的图片

调用相机&#xff08;隐式调用&#xff09; //自定义一个请求码 这里我设为10010int TAKE_PHOTO_REQUEST 10010;int RESULT_CANCELED 0;//定义取消码//触发监听&#xff0c;调用相机image_camera.setOnClickListener(new View.OnClickListener() {Overridepublic void onCli…...

编程日记 2023/9/21 18:57:45

企业如何找媒体发稿能收录且不被拒稿，媒介盒子无偿分享

媒平台像头条、百家号、微信、微博、搜狐等平台&#xff0c;都支持全自助发稿&#xff0c;拥有庞大的用户群体。也正是因为这些平台的发展&#xff0c;衍生出了一大批自媒体KOL&#xff0c;影响力与传统媒体不相上下甚至更胜。 媒体宣发是企业营销的必要途径之一。软文是成本低…...

编程日记 2023/9/21 18:56:43

利用cms主题构造木马(CVE-2022-26965)

简介 CVE-2022-26965是Pluck CMS 4.7.16版本存在一个远程shell上传执行漏洞。 攻击者可利用此漏洞通过构造恶意的主题包进行上传并执行&#xff0c;未经授权访问服务器&#xff0c;造成潜在的安全隐患。 过程 1.打开环境&#xff0c;查看源码&#xff0c;发现login.php 2.进…...

编程日记 2023/9/21 18:55:43

【MTK】【WFD】手机投屏到投影仪不显示画面

问题分析： 在投屏过程中，有时候会出现WFD sink端回复的video 格式表不正确，sink表示是支持VESA（3fffffff），但是当手机根据协商结果得到最优分辨率并发送给sink端时，sink端看上去没有正常播放，其实实际上应该是不支持的。 比如我们这个问题就是CES表中的0001ffff，最大…...

编程日记 2023/9/21 18:54:42

多输入多输出 | MATLAB实现PSO-LSSVM粒子群优化最小二乘支持向量机多输入多输出

多输入多输出 | MATLAB实现PSO-LSSVM粒子群优化最小二乘支持向量机多输入多输出 目录 多输入多输出 | MATLAB实现PSO-LSSVM粒子群优化最小二乘支持向量机多输入多输出预测效果基本介绍程序设计往期精彩参考资料 预测效果 基本介绍 MATLAB实现PSO-LSSVM粒子群优化最小二乘支持向…...

编程日记 2023/9/21 18:51:39

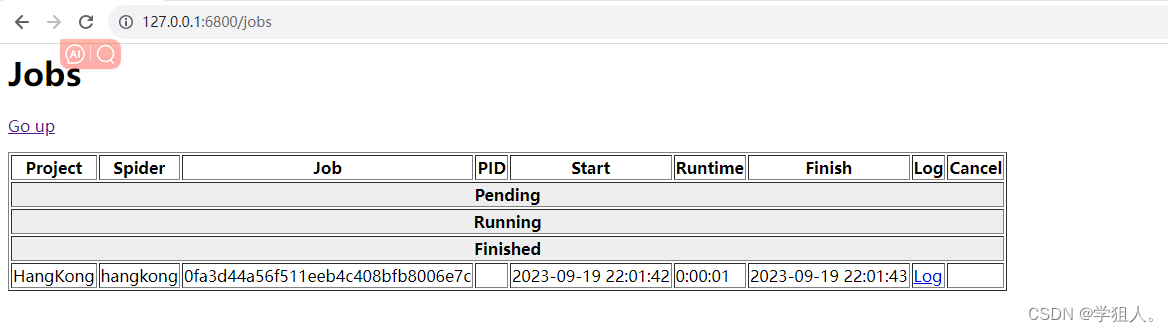
scrapyd-完整细节

安装scrapyd服务 pip install scrapyd 安装scrapyd客户端 pip install scrapyd-client 安装好以后重新开启cmd输入命令 scrapyd 出现以下结果代表安装成功 打开浏览器输入网址&#xff0c;即可打开界面客户端 http://127.0.0.1:6800/ 回车后显示一下ok内容代表部署成功 回到服…...

编程日记 2023/9/21 18:50:38

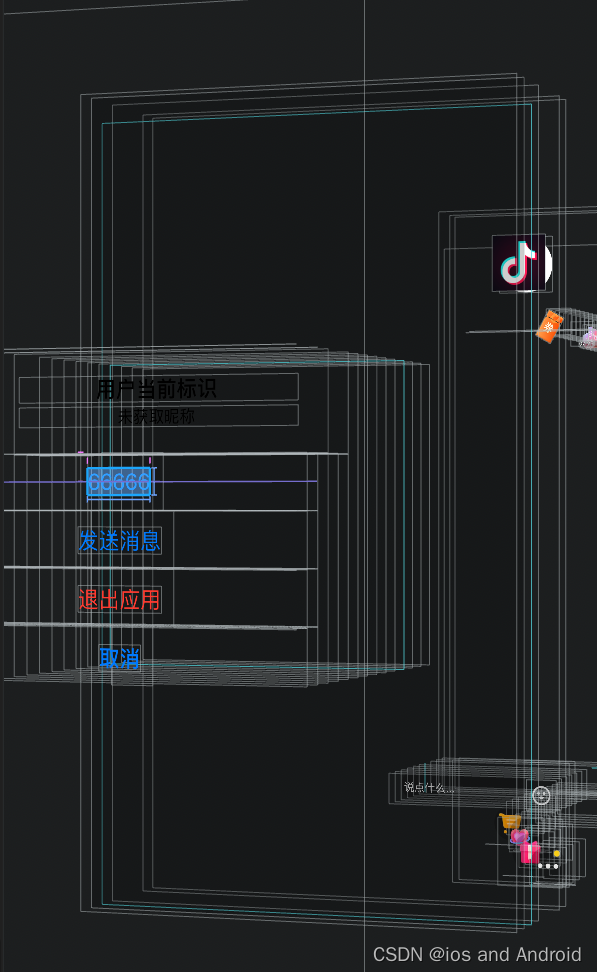
【iOS逆向与安全】插件开发之某音App直播间自动发666

1.目标 由于看直播的时候主播叫我发 666&#xff0c;支持他&#xff0c;我肯定支持他呀&#xff0c;就一直发&#xff0c;可是后来发现太浪费时间了&#xff0c;能不能做一个直播间自动发 666 呢&#xff1f;于是就花了几分钟做了一个。 2.操作环境 越狱iPhone一台 frida ma…...

编程日记 2023/9/21 18:48:36

CTF show Web 红包题第六弹

提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框&#xff0c;很难让人不联想到SQL注入&#xff0c;但提示都说了不是SQL注入&#xff0c;所以就不往这方面想了 ​ 先查看一下网页源码&#xff0c;发现一段JavaScript代码&#xff0c;有一个关键类ctfs…...

编程新知 2026/1/30 16:12:20

ubuntu搭建nfs服务centos挂载访问

在Ubuntu上设置NFS服务器 在Ubuntu上&#xff0c;你可以使用apt包管理器来安装NFS服务器。打开终端并运行&#xff1a; sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享&#xff0c;例如/shared&#xff1a; sudo mkdir /shared sud…...

编程新知 2026/1/12 14:38:19

Go 语言接口详解

Go 语言接口详解 核心概念 接口定义 在 Go 语言中&#xff0c;接口是一种抽象类型&#xff0c;它定义了一组方法的集合&#xff1a; // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的&#xff1a; // 矩形结构体…...

编程新知 2026/1/4 5:19:25

cf2117E

原题链接&#xff1a;https://codeforces.com/contest/2117/problem/E 题目背景&#xff1a; 给定两个数组a,b&#xff0c;可以执行多次以下操作&#xff1a;选择 i (1 < i < n - 1)&#xff0c;并设置 或&#xff0c;也可以在执行上述操作前执行一次删除任意 和 。求…...

编程新知 2026/1/31 9:25:30

Matlab | matlab常用命令总结

常用命令 一、 基础操作与环境二、 矩阵与数组操作（核心）三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结，涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

编程新知 2025/8/11 1:05:59

NFT模式：数字资产确权与链游经济系统构建

NFT模式&#xff1a;数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新&#xff1a;构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议&#xff1a;基于LayerZero协议实现以太坊、Solana等公链资产互通&#xff0c;通过零知…...

编程新知 2026/1/31 23:23:23

【JavaSE】绘图与事件入门学习笔记

-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角&#xff0c;以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向&#xff0c;距离坐标原点x个像素;第二个是y坐标&#xff0c;表示当前位置为垂直方向&#xff0c;距离坐标原点y个像素。 坐标体系-像素 …...

编程新知 2025/12/19 20:46:15

3-11单元格区域边界定位(End属性)学习笔记

返回一个Range 对象&#xff0c;只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意&#xff1a;它移动的位置必须是相连的有内容的单元格…...

编程新知 2026/1/20 19:15:45

智能分布式爬虫的数据处理流水线优化：基于深度强化学习的数据质量控制

在数字化浪潮席卷全球的今天&#xff0c;数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具&#xff0c;在大规模数据获取中发挥着关键作用。然而&#xff0c;传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时&#xff0c;常出现数据质…...

编程新知 2026/1/20 22:51:34

docker 部署发现spring.profiles.active 问题

报错&#xff1a; org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

编程新知 2025/9/20 12:14:18