想要精通算法和SQL的成长之路 - 预测赢家
想要精通算法和SQL的成长之路 - 预测赢家
- 前言
- 一. 预测赢家
- 二. 石子游戏(预测赢家的进阶版)
- 2.1 博弈论
前言
想要精通算法和SQL的成长之路 - 系列导航
一. 预测赢家
原题链接

主要思路:
- 我们定义
dp[i][j]:在区间[i, j]之间先手情况下能拿到的相对分数。 - 因为玩家1是先手,那么我们站在玩家1的角度来思考,在区间
[i, j]之间,如果玩家1选择最左侧,值为num[i]。那么玩家2只能在[i-1,j]区间内选择,并且是先手。那么他能拿到的最大相对分数就是:dp[i+1][j]。那么此时玩家1选择左手时的相对分数就是:num[i] - dp[i+1][j]。 - 同理如果玩家1先手选择最右侧,那么此时玩家1选择左手时的相对分数就是:
num[j] - dp[i][j-1]。 - 那么本次玩家1应该选择利益最大化的,即:
Max(num[i] - dp[i+1][j], num[j] - dp[i][j-1])。 - 只要这个值 >=0 (相对分数,差值)玩家1就是胜利者。
代码如下:
public boolean predictTheWinner(int[] nums) {return dfs(0, nums.length - 1, nums) >= 0;
}public int dfs(int left, int right, int[] nums) {// 遍历完了,返回0if (left > right) {return 0;}// 选择最左侧时的最大相对差值int chooseLeft = nums[left] - dfs(left + 1, right, nums);// 选择最右侧时的最大相对差值int chooseRight = nums[right] - dfs(left, right - 1, nums);// 返回最大相对差值return Math.max(chooseLeft, chooseRight);
}
当然,这类递归性质的代码,往往都存在一些重复计算的动作,我们用一个全局的数组,来记录递归过程中计算出来的值,即:记忆化搜索。
private int[][] memo;public boolean predictTheWinner(int[] nums) {int len = nums.length;memo = new int[len][len];// 初始化一个比较特殊的值,用于判断是否计算过for (int i = 0; i < len; i++) {Arrays.fill(memo[i], Integer.MAX_VALUE);}return dfs(0, nums.length - 1, nums) >= 0;
}public int dfs(int left, int right, int[] nums) {if (left > right) {return 0;}// 记忆化搜索,如果搜索过,直接返回if(memo[left][right] != Integer.MAX_VALUE) {return memo[left][right];}// 如果当前先手,选择左边的数,那么后手就是:dfs(left + 1, right, nums),计算后手的最大值,我们求此时先后手的相对值int chooseLeft = nums[left] - dfs(left + 1, right, nums);int chooseRight = nums[right] - dfs(left, right - 1, nums);return memo[left][right] = Math.max(chooseLeft, chooseRight);
}
二. 石子游戏(预测赢家的进阶版)
原题链接
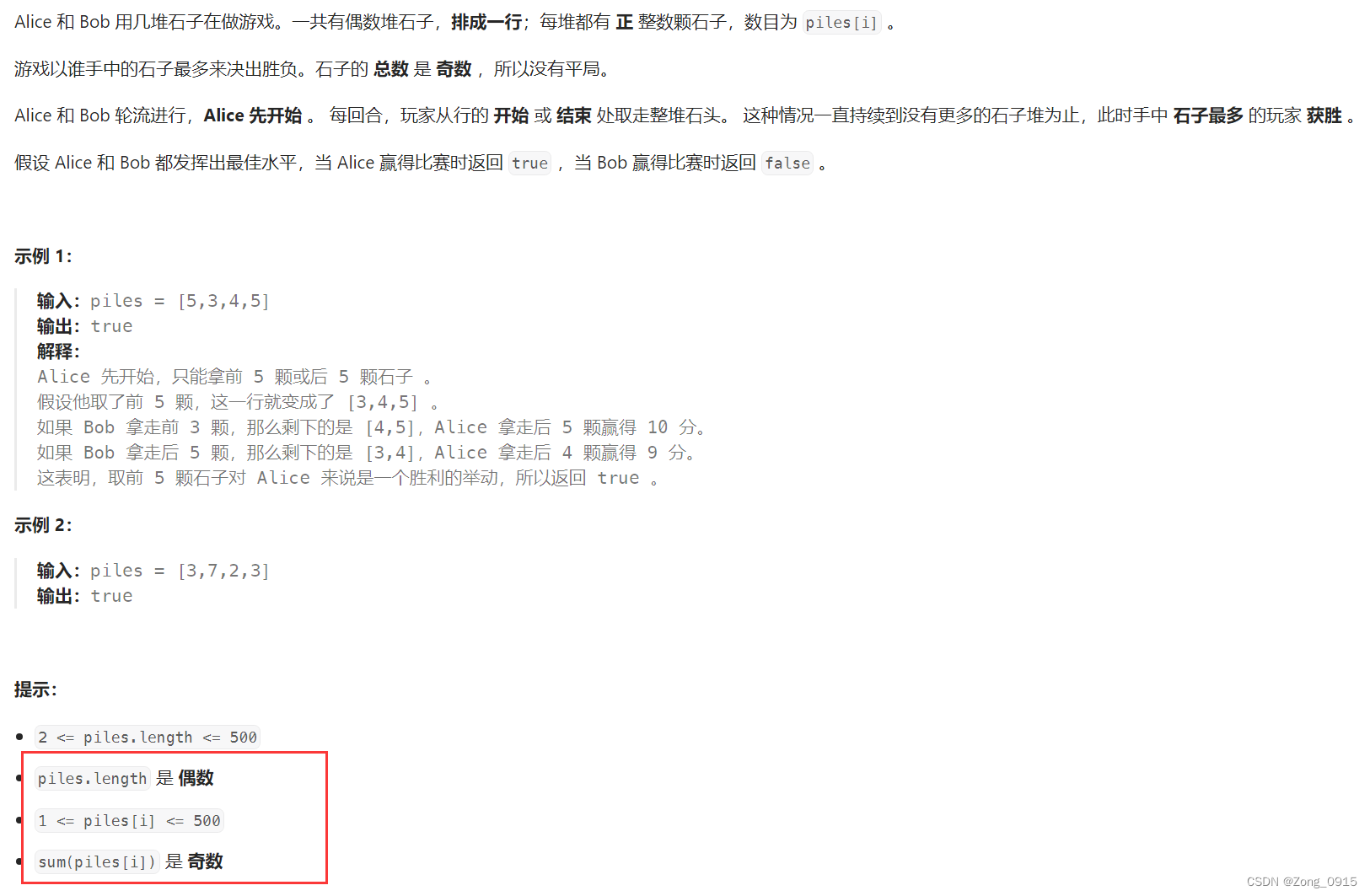
这个题目相当于在第一题的基础上多了两个条件:
- 石头总数为奇数。
- 堆数为偶数。
也就是说不可能存在平局的情况。
2.1 博弈论
在满足上述两个条件的基础上:先手必胜。
我们假设一个数组如下:[奇, 偶, 奇, 偶, 奇, 偶, 奇, 偶, 奇, 偶, 奇, 偶]。
- 那么对于先手而言:他能选择的序列为:奇偶序列(头和尾)[
奇, 偶, 奇, 偶, 奇, 偶, 奇, 偶, 奇, 偶, 奇,偶]。 - 那么对于后手而言:如果先手选择的是奇数,那么后手选择的序列只能是偶偶序列。[“先手选的”,
偶, 奇, 偶, 奇, 偶, 奇, 偶, 奇, 偶, 奇,偶]。反之同理,只能选择奇奇序列。
总之就是:先手必定是奇偶性不同的局面。后手必定是奇偶性相同的局面。
那么问题简单了,我们只需要知道,奇序列的总和 和 偶序列总和 谁大,然后先手每次决策的时候,限制对方只能选择奇偶序列的对立面即可。
因此题目中既然说明了Alice先手的情况,我们直接返回true就完事了。
public boolean stoneGame(int[] piles) {return true;
}
相关文章:

想要精通算法和SQL的成长之路 - 预测赢家
想要精通算法和SQL的成长之路 - 预测赢家 前言一. 预测赢家二. 石子游戏(预测赢家的进阶版)2.1 博弈论 前言 想要精通算法和SQL的成长之路 - 系列导航 一. 预测赢家 原题链接 主要思路: 我们定义dp[i][j]:在区间 [i, j] 之间先…...
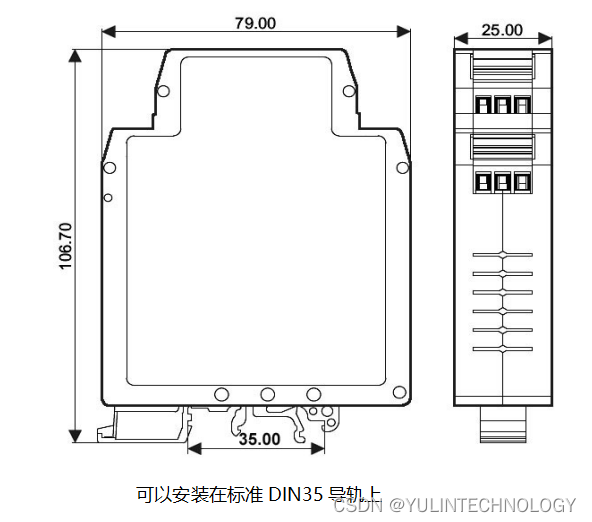
高精度PWM脉宽调制信号转模拟信号隔离变送器1Hz~10KHz转0-5V/0-10V/1-5V/0-10mA/0-20mA/4-20mA
主要特性: >>精度等级:0.1级。产品出厂前已检验校正,用户可以直接使用 >>辅助电源:8-32V 宽范围供电 >>PWM脉宽调制信号输入: 1Hz~10KHz >>输出标准信号:0-5V/0-10V/1-5V,0-10mA/0-20mA/4-20mA等&…...
Vue路由和Node.js环境搭建
文章目录 一、vue路由1.1 简介1.2 SPA1.3 实例 二、Node.js环境搭建2.1 Node.js简介2.2 npm2.3 环境搭建2.3.1 下载解压2.3.2 配置环境变量2.3.3 配置npm全局模块路径和cache默认安装位置2.3.4 修改npm镜像提高下载速度 2.4 运行项目 一、vue路由 1.1 简介 Vue 路由是 Vue.js…...

【Vue】使用vue-cli搭建SPA项目的路由,嵌套路由
一、SPA项目的构建 1、前期准备 我们的前期的准备是搭建好Node.js,测试: node -v npm -v2、利用Vue-cli来构建spa项目 2.1、什么是Vue-cli Vue CLI 是一个基于 Vue.js 的官方脚手架工具,用于自动生成vue.jswebpack的项目模板,它可以帮助开发者…...
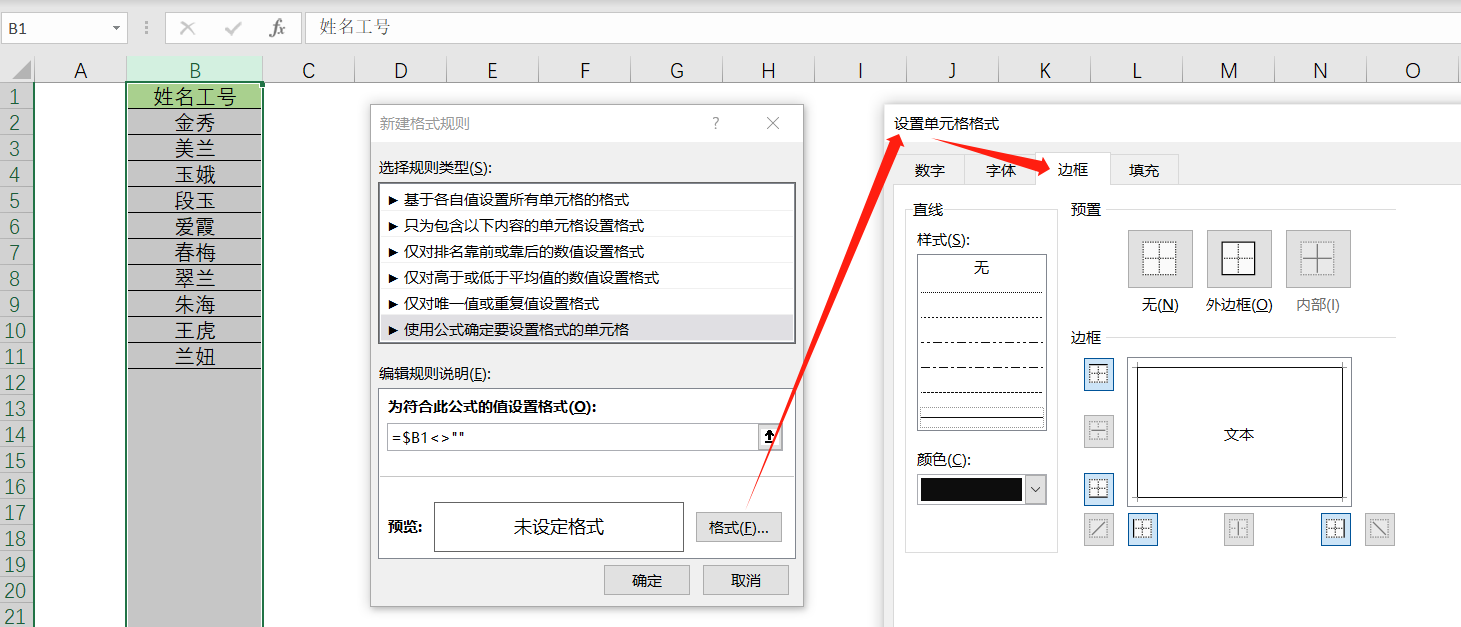
Excel 通过条件格式自动添加边框
每录入一次数据就需要手动添加一次边框,非常麻烦,这不是我们想要的。 那么有没有办法,在我们录入数据后,自动帮我们加上边框呢? 选中要自动添加边框的列,然后按箭头流程操作 ↓ ↓ ↓ ↓...

mysql 备份和还原 mysqldump
因window系统为例 在mysql安装目录中的bin目录下 cmd 备份 备份一个数据库 mysqldump -uroot -h hostname -p 数据库名 > 备份的文件名.sql 备份部分表 mysqldump -uroot -h hostname -p 数据库名 [表 [表2…]] > 备份的文件名.sql ## 多个表 空格隔开,中间…...

ELK日志分析系统+ELFK(Filebeat)
本章结构: 1、ELK日志分析系统简介 2、Elasticsearch介绍(简称ES) 3、Logstash介绍 4、Kibana介绍 5、实验,ELK部署 一、ELK日志分析系统简介 ELK平台是一套完整的日志集中处理解决方案,将 ElasticSearch、Logst…...

ULID 在 Java 中的应用: 使用 `getMonotonicUlid` 生成唯一标识符
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...
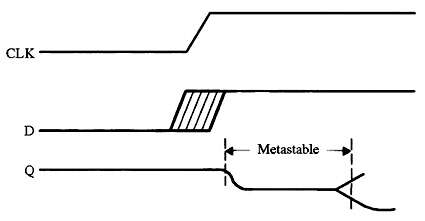
实用的嵌入式编码技巧:第三部分
每个触发器都有两个我们在风险方面违反的关键规格。“建立时间”是时钟到来之前输入数据必须稳定的最小纳秒数。“保持时间”告诉我们在时钟转换后保持数据存在多长时间。 这些规格因逻辑设备而异。有些可能需要数十纳秒的设置和/或保持时间;其他人则需要少一个数量…...

8个很棒的Vue开发技巧
1.路由参数解耦 通常在组件中使用路由参数,大多数人会做以下事情。 export default { methods: {getParamsId() {return this.$route.params.id} } } 在组件中使用 $route 会导致与其相应路由的高度耦合,通过将其限制为某些 URL 来限制组件的灵活性。…...

Python - 小玩意 - 文字转语音
import pyttsx3 from tkinter import *def recognize_and_save():try:say pyttsx3.init()rate say.getProperty(rate) # 获取当前语速属性的值say.setProperty(rate, rate - 20) # 设置语速属性为当前语速减20text text_var.get()# 语音识别say.say(text)say.runAndWait()…...
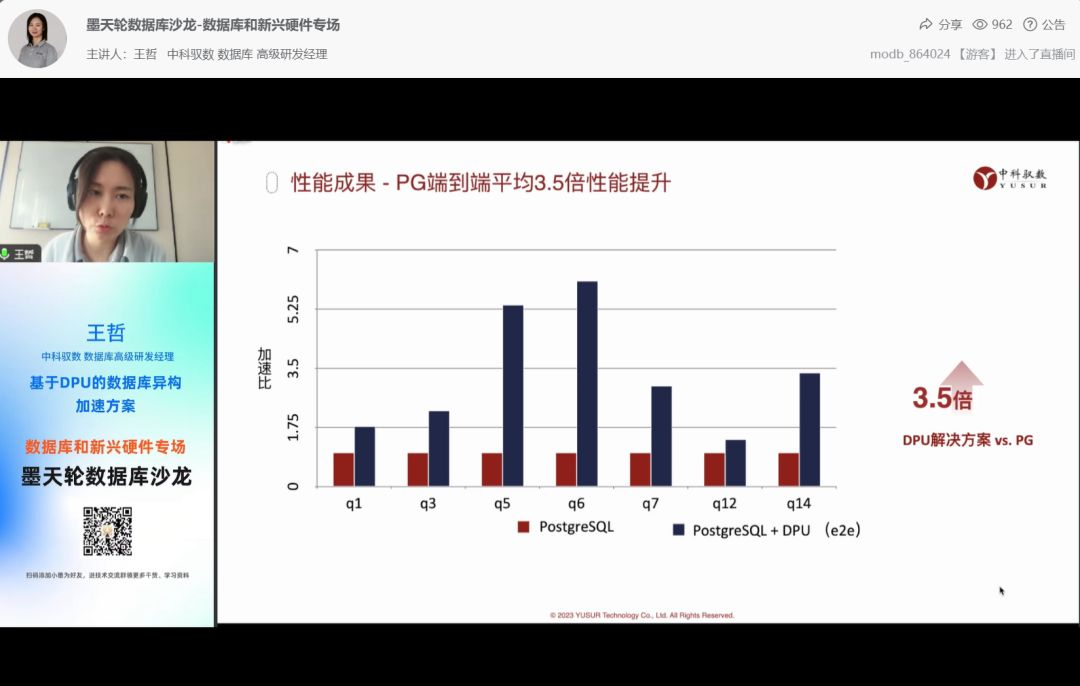
聚焦数据库和新兴硬件的技术合力 中科驭数受邀分享基于DPU的数据库异构加速方案
随着新型硬件成本逐渐降低,充分利用新兴硬件资源提升数据库性能是未来数据库发展的重要方向之一,SIGMOD、VLDB、CICE数据库顶会上出现越来越多新兴硬件的论文和专题。在需求侧,随着数据量暴增和实时性的要求越来越高,数据库围绕处…...

哨兵模式(sentinel)
为什么需要哨兵模式 redis的主从复制模式能够缓解“读压力”,但是存在两个明显问题。 主节点发生故障,进行主节点切换的过程比较复杂,需要人工参与,导致故障恢复时间无法保障主节点通过主从复制模式将读压力分散出去,…...

b站老王 自动驾驶决策规划学习记录(十二)
自动驾驶之速度规划详解:SL与ST迭代 上一讲:b站老王 自动驾驶决策规划学习记录(十一) 接着上一讲学习记录b站老王对自动驾驶规划系列的讲解 参考视频: 自动驾驶决策规划算法第二章第七节(上) 速度规划详解:SL与ST迭代…...

服务器租用机房机房的类型应该如何选择
服务器租用机房机房的类型应该如何选择 1.单电信机房 单电信服务器机房业务模式比较固定,访问量也不是很大,适合新闻类网站或政务类网站。如果网站的PV流量持续增加,建议后期采用租赁CDN的方式解决非电信用户访问网站速度过慢的问题。 2.双线…...

大数据运维一些常见批量操作命令
大数据运维中,批量操作是一项常见的任务。在使用flume进行数据采集的过程中,有时会出现故障导致采集停止,此时积累了大量的文件。如果想要将这些文件迁移到新的目录,直接使用"mv"命令可能会因为文件数目过多而报错。为了…...

测试人职场生存必须避开的5个陷阱
在互联网职场的工作发展道路上,软件测试人员其实在公司中也面临着各种各样的职场陷阱,有些可能是因为项目业务不熟练造成的,有些可能是自身技术能力不足导致的...等等。软件测试入门相对来说比较容易些,但是想要在测试行业长久发展…...

力扣538 补9.18
538.把二叉搜索树转换为累加树 可以做,主要还是分类讨论并找规律。 当前结点如果是左节点的话,root.valroot.valpre.valdfs(root.right); 如果是右结点的话, root.valpre.val-preval-dfs(root.left); 都和前一个结点有关系,如…...

[Linux入门]---Linux编译器gcc/g++使用
文章目录 1.背景知识2.gcc如何完成编译运行工作预处理(进行宏替换)编译(生成汇编)汇编(生成机器可识别代码)链接(生成可执行文件) 3.函数库动态库静态库动静态库的区别 4.gcc选项 1.…...
[Git入门]---gitee注册及代码提交
文章目录 1.Gitee是什么2.gitee注册3.git工具及图形化界面工具安装4.gitee仓库创建5.进行本地仓库与远端gitee仓库的链接6.git三板斧addcommitpush 7.gitee提交代码常见问题 1.Gitee是什么 gitee是基于git代码托管和研发协作的国内平台,在上面可以托管个人或公司代…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...
