算法通关村第十五关——从40亿个数中产生一个不存在的数的处理方法
1.从40个亿中产生一个不存在的整数
题目要求:给定一个输入文件,包含40亿个非负整数,请设计一个算法,产生一个不存在该文件中的整数,假设你有1GB的内存来完成这项任务。****
解题中心思想:存储的不是这40亿个数据本身,而是其对应的位置。
本题不用写代码,能把方法过程说清楚就可以。
1.1 位图存储大数据的原理
方法:8 bit 为 1B,一个32位整数需要4B的存储空间,40亿个数就是 40亿 * 4B,约为16GB,用位图来做的话会更节省空间,因为位图的每个位置只能用0或1进行状态表示,这样就只需要40亿 / 8 = 5亿字节,也就是大约500M的存储空间。
过程:具体来做就是先遍历这40亿个数,并把遍历的每个数在位图上的相对位置设置为1。这40亿个数遍历结束后,开始遍历位图,看看哪个位置上的状态为0,就说明这个位置对应的数没有在40亿个数中出现,位图遍历结束后就能得到所有未在40亿个数中出现过的数。
1.2 使用10MB来存储呢?
如果使用10MB来存储,位图也搞不定了,这个时候就得使用分块思想,用时间换空间,通过两次遍历来处理。
40亿个数需要约500MB的空间,如果只有10MB的空间,至少需要50个块才可以。一般划分块都使用2的幂次方的整数倍,此处划分为64个块是合理的。
首先将 0 − 2 32 0-2^{32} 0−232 这个范围的数平均分成64个区间,每个区间是67 108 864个数,因为一共只有40亿个数,所以在统计每一个区间上的数有多少时,肯定会有至少一个区间上的计数小于67 108 864。利用这一点可以找出其中一个没出现过的数。具体过程如下:
第一次遍历:先申请长度位64的整型数组countArr[0, ..., 63],countArr[i]用来统计区间i上的数有多少。遍历40亿个数,跟去当前数是多少来决定哪一个区间上的计数增加。比如,如果当前数为2 567 278 189,2 567 278 189 / 67 108 864 = 38 ,所以第38个区间上计数增加countArr[51]++。遍历完40亿个数之后,遍历countArr,必然会有某一个位置上的值(countArr[i])小于67 108 864,表示第i区间上至少有一个数没出现过。
此时使用的内存是非常小的,是countArr的大小(64 * 4B)
假设找到第37区间上的计数小于67 108 864,那么对这40亿个数据进行第二次遍历:
- 申请长度为
67 108 864的位图(bit map),占用大约8MB的空间,记为bitArr[0, ... , 67108863]。 - 遍历这40亿个数,此时的遍历只关注落在第37区间上的数,记为
num(num满足num / 67108864 = == 37),其他区间的数全部忽略。 - 如果步骤2的
num在第37区间上,将bitArr[num - 67108864 * 37]的值设置为1,也就是只做第37区间上的数的bitArr映射。 - 遍历完40亿个数之后,在
bitArr上必然存在没被设置成1的位置,假设第i个位置上的值没被设置成1,那么67108864 * 37 + i这个数就是一个没出现过的数
步骤小结:
- 根据 10MB 的内存限制,确定统计区间的大小,就是第二次遍历时的 bitArr 大小。
- 利用区间计数的方式,找到那个计数不足的区间,这个区间上肯定有没出现的数。
- 对这个区间上的数做 bit map 映射,再遍历bit map,找到一个没出现的数即可。
1.3 如何确定分块的区间
上面的例子中,采用两次遍历,第一次将数据分成64块刚好解决问题,为什么不是128块,32块,16块或者其他块数呢?
这是主要为了保障第二次遍历时每个块都能放进这10MB的空间中。 2 23 < 10 M B < 2 24 2^{23} < 10MB < 2^{24} 223<10MB<224,而 2 23 = 8388608 2^{23} = 8388608 223=8388608 大约是8MB,也就是说我们一次的分块大小只能为8MB左右。我们在第二次遍历时分成64块刚好满足要求,这是最少得分成64块,当然如果分成128块、256块也是可以的。
相关文章:

算法通关村第十五关——从40亿个数中产生一个不存在的数的处理方法
1.从40个亿中产生一个不存在的整数 题目要求:给定一个输入文件,包含40亿个非负整数,请设计一个算法,产生一个不存在该文件中的整数,假设你有1GB的内存来完成这项任务。**** 解题中心思想:存储的不是这40亿…...

软件项目开发的流程及关键点
软件项目开发的流程及关键点 graph LR A[需求分析] --> B[系统设计] B --> C[编码开发] C --> D[测试验证] D --> E[部署上线] E --> F[运维支持]在项目开发的流程中,首先是进行需求分析,明确项目的目标和功能要求。接下来是系统设计&am…...
)
全球变暖问题(floodfill 处理联通块问题)
全球变暖问题 文章目录 全球变暖问题前言题目描述题目分析边界问题的考虑岛屿是否被淹没判断:如何寻找联通块: 代码预告 前言 之前我们介绍了 bfs算法在二维,三维地图中的应用,现在我们接续进行拓展,解锁floodfill 算…...

由于找不到vcruntime140_1.dll怎么修复,详细修复步骤分享
在使用电脑过程中,可能会遇到一些错误提示,其中之一是找不到vcruntime140_1.dll的问题。这使得许多用户感到困扰,不知道该如何解决这个问题。小编将详细介绍vcruntime140_1.dll的作用以及解决找不到该文件的方法,帮助你摆脱困境。…...
)
算法 三数之和-(双指针)
牛客网: BM54 题目: 数组中所有不重复的满足三数之和等于0的数,非递减形式。 思路: 数组不小于3。不重复非递减,需先排序。使用idx从0开始遍历到n-2, 如果出现num[idx]num[idx-1]的情况,忽略继续下一个idx;令left idx1, right …...
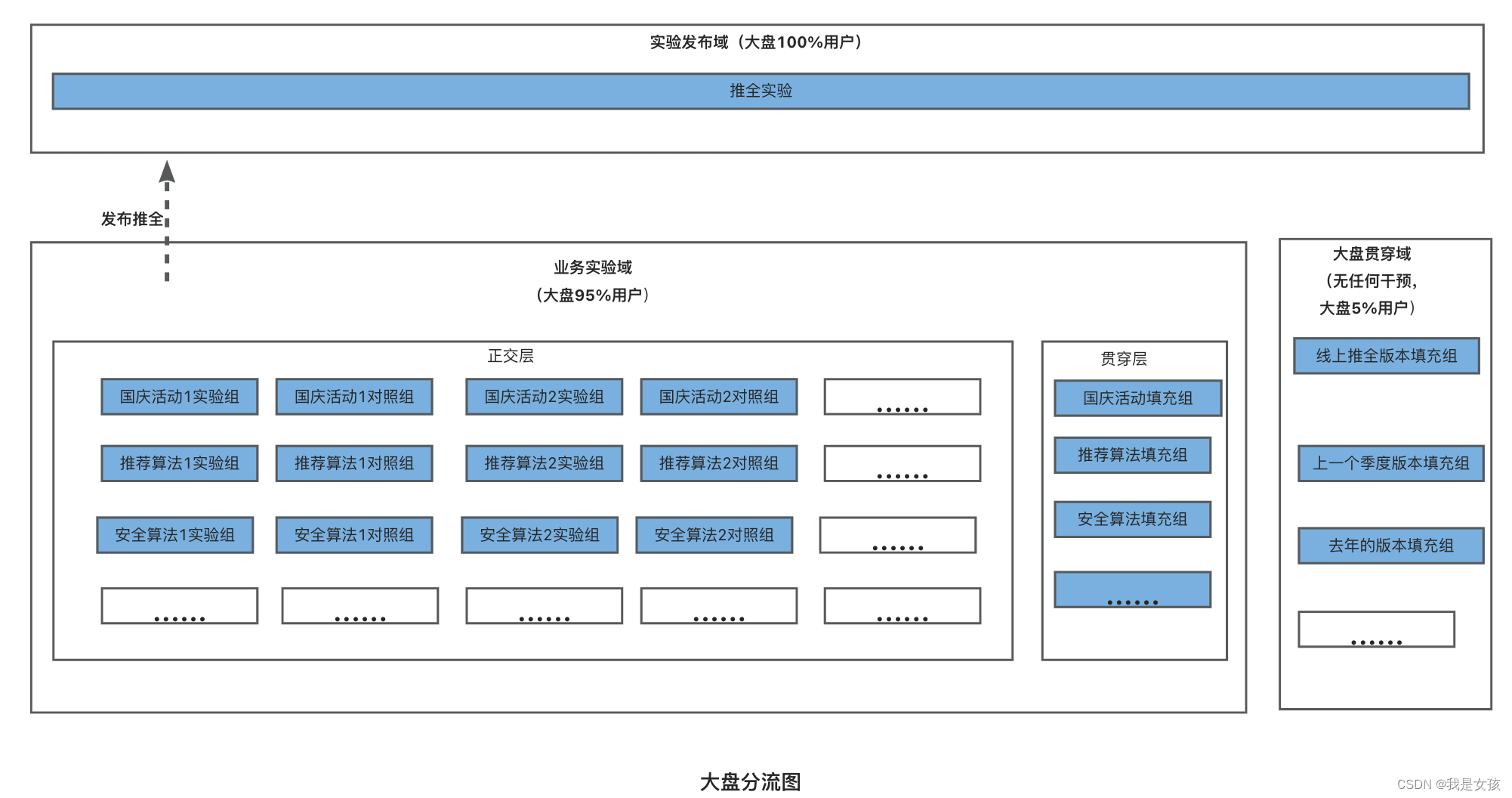
AB实验总结
互联网有线上系统,可做严格的AB实验。传统行业很多是不能做AB实验的。 匹配侧是采用严格的AB实验来进行模型迭代,而精细化定价是不能通过AB实验来评估模型好坏,经历过合成控制法、双重差分法,目前采用双重差分法来进行效果评估。…...

sklearn包中对于分类问题,如何计算accuracy和roc_auc_score?
1. 基础条件 import numpy as np from sklearn import metricsy_true np.array([1, 7, 4, 6, 3]) y_prediction np.array([3, 7, 4, 6, 3])2. accuracy_score计算 acc metrics.accuracy_score(y_true, y_prediction)这个没问题 3. roc_auc_score计算 The binary and mul…...

python温度转换程序
1.使用pycharm运行温度转换程序,尝试将温度单位设在前面 2.参照温度转换程序,自己写一个关于货币转换、长度转换、重量转换或者面积转换的程序 循环函数 def convertemperature():temperature ""while (temperature ! "q"):temperature in…...

Vue2中10种组件通信方式和实践技巧
目录 1,props / $emit1.1,一个需求方法1方法2 1.2,v-model 和 .syncv-model.sync 2,$children / $parent3,ref4,$attrs / $listeners$attrs$listenersinheritAttrs1.1 的问题的第3种解决方法 5,…...
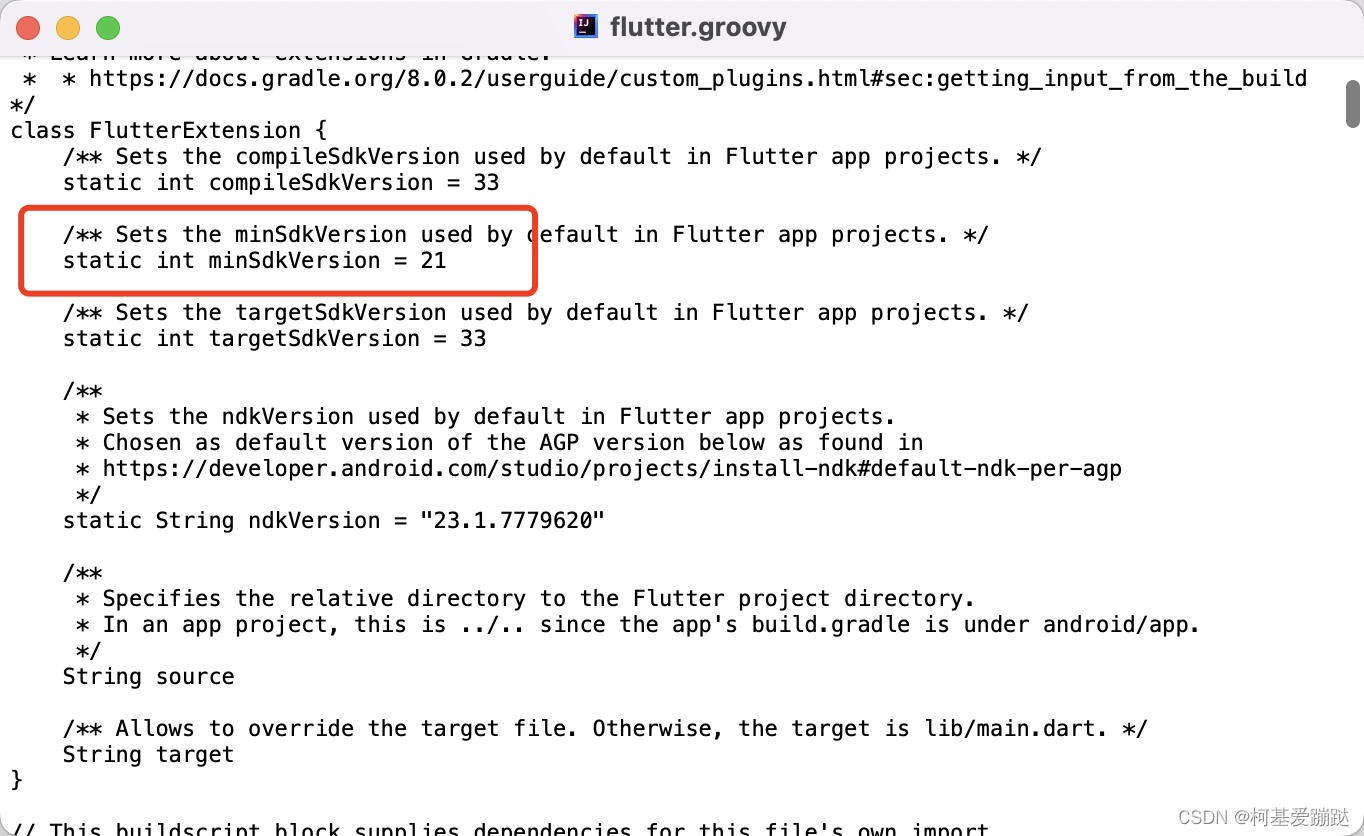
Flutter flutter.minSdkVersion的实际文件位置
Flutter 项目的Android相关版本号配置: flutter.minSdkVersion 的版本号配置文件实际路径: …/flutter_sdk/packages/flutter_tools/gradle/src/main/groovy/flutter.groovy Flutter版本号如下: bzbMacBook-Pro ccsmec % flutter --version …...
python生成PDF报告
前言 最近接到了一个需求-将项目下的样本信息汇总并以PDF的形式展示出来,第一次接到这种PDF的操作的功能,还是有点慌的,还好找到了reportlab这个包,可以定制化向PDF写内容! 让我们由简入深进行讲解 一、reportlab是…...
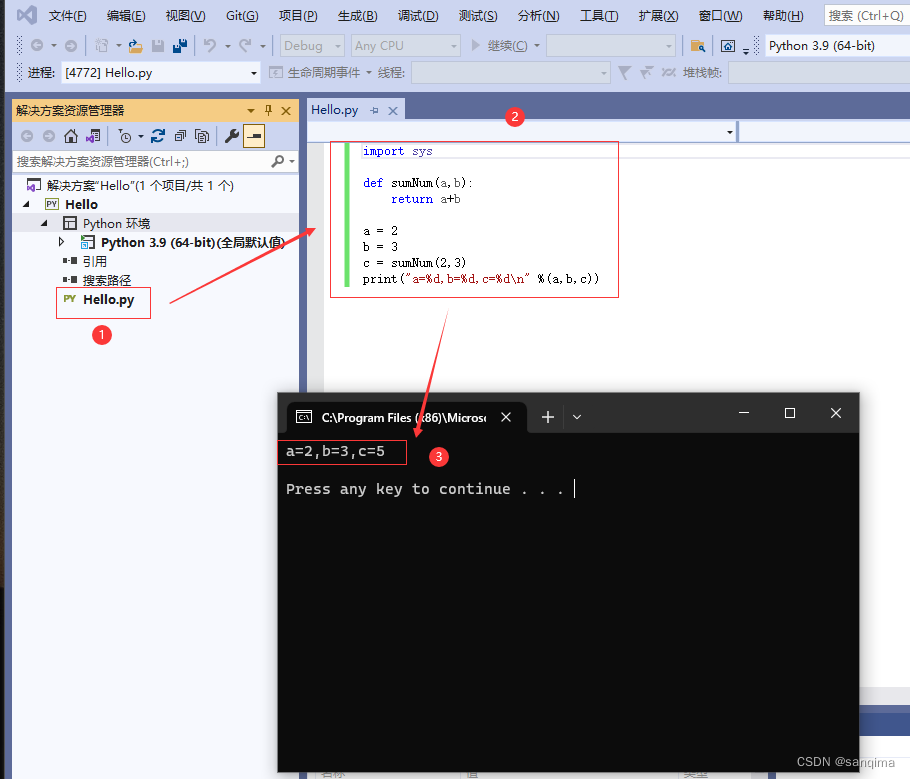
在visual studio里安装Python并创建python工程
在2009年,云计算开始发力,Python、R、Go这些天然处理批量计算的语言也迅猛发展。微软在2010年,把Python当成一个语言包插件,集成到了visual studio 2010里。在"云优先,移动优先"的战略下,于2015年…...
试用 6 -- 从简单到复杂)
AIGC(生成式AI)试用 6 -- 从简单到复杂
从简单到复杂,这样的一个用例该如何设计? 之前浅尝试用,每次尝试也都是由浅至深、由简单到复杂。 一点点的“喂”给生成式AI主题,以测试和验证生成式AI的反馈。 AIGC(生成式AI)试用 1 -- 基本文本_Role…...
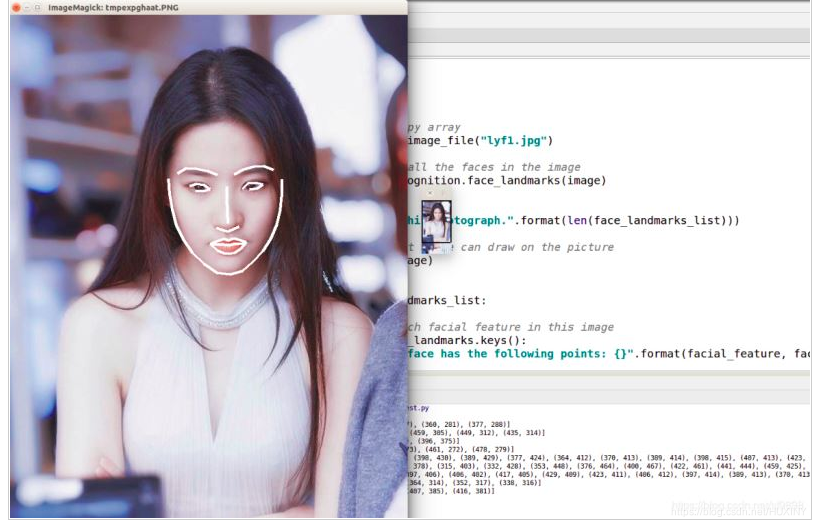
竞赛 基于深度学习的人脸识别系统
前言 🔥 优质竞赛项目系列,今天要分享的是 基于深度学习的人脸识别系统 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐! 🧿 更多资料, 项目分享: https://gitee.com/dancheng-senior/…...

uniapp:APP开发,后台保活
前言: 在ios中,软件切换至后台、手机息屏,过了十来秒软件就会被系统挂起,APP内的任务就不能继续执行;在android中,默认情况下,软件在后台运行的时候,触发某些特定条件的情况下&…...
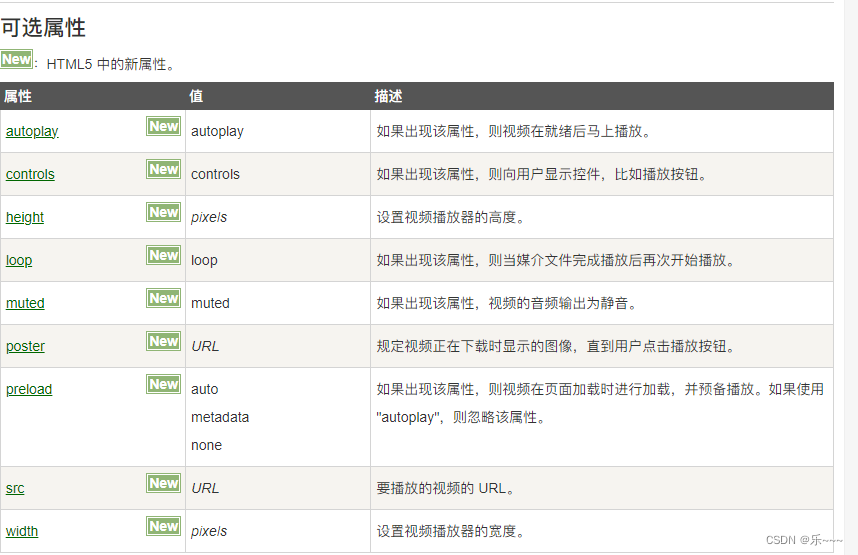
vue2 项目中嵌入视频
案例: 代码: <template><div class"schematicDiagramIndex"><el-container><el-aside width"20rem"> <!-- <h4 style"font-size: 18px">视频演示</h4>--><div styl…...

第二章 进程与线程 十二、进程同步与进程互斥
目录 一、进程同步 1、定义 二、进程互斥 1、定义 2、四个部分 3、原则 一、进程同步 1、定义 进程同步是指在多个进程之间协调执行顺序的一种机制,使得进程按照一定的顺序执行,以避免出现不一致的情况。常见的实现方式有信号量、管程、屏障等。…...
移植到任意平台)
Linux内核链表(list)移植到任意平台
一、前言 linux内核链表在include/linux/list.h文件中,内核中实现的链表比较简洁,实用性很强,因此想把它单独移植出来使用。 内核中的代码只能使用gnuc编译器编译,stdc编译器编译是会报错的,主要是因为typeof这个宏是…...

【操作系统】聊聊什么是CPU上下文切换
对于linux来说,本身就是一个多任务运行的操作系统,运行远大于CPU核心数的程序,从用户视角来看是并发执行,而在CPU视角看其实是将不同的CPU时间片进行分割,每个程序执行一下,就切换到别的程序执行。那么这个…...

CMake教程-第 2 步 添加一个库
CMake教程-第 2 步 添加一个库 1 CMake教程介绍2 学习步骤Step 1: A Basic Starting PointStep 2: Adding a LibraryStep 3: Adding Usage Requirements for a LibraryStep 4: Adding Generator ExpressionsStep 5: Installing and TestingStep 6: Adding Support for a Testin…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...
