求二维子数组的和(剖析)
文章目录
- 🐒个人主页
- 🏅JavaSE系列专栏
- 📖前言:本篇剖析一下二维子数组求和
- 规则:
🐒个人主页
🏅JavaSE系列专栏
📖前言:本篇剖析一下二维子数组求和
规则:
这是一个4 X 4的二维数组a[][]
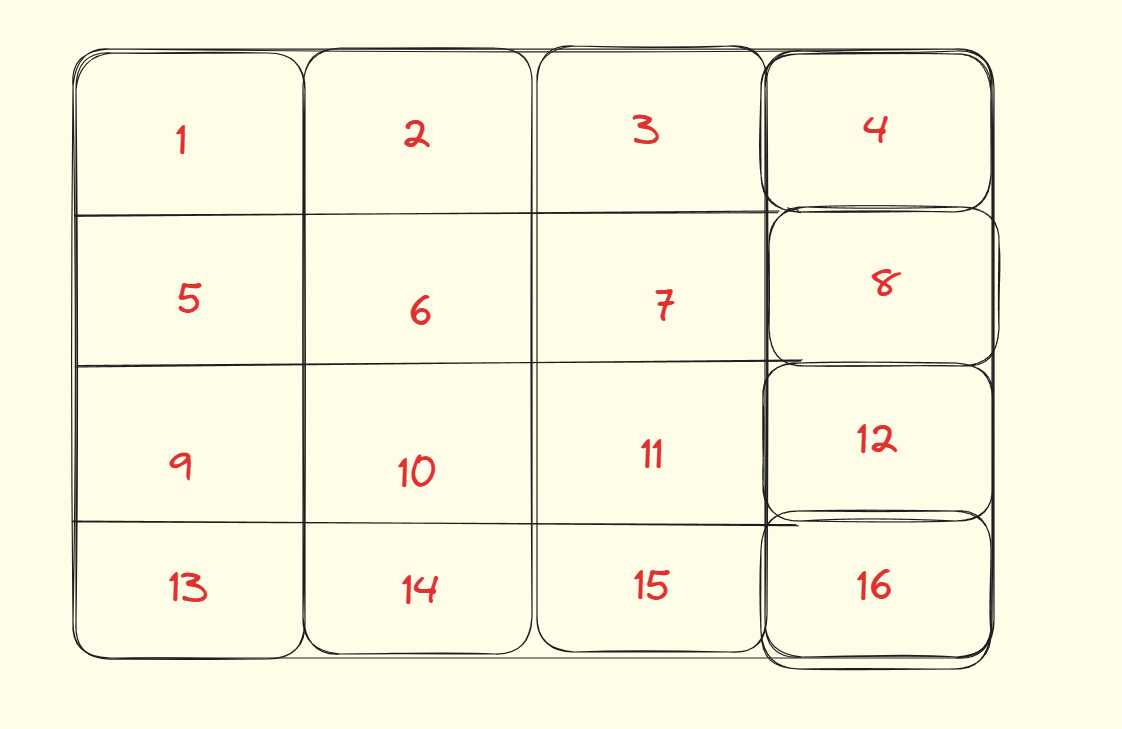
假设再来一个4 X 4的空数组,
第一个位置是a[0][0],(前一个元素的和)
第二个位置是a[0][0]+a[0][1]+a[0][2],(前两个元素的和)
第三个位置是a[0][0]+a[0][1]+a[0][2],(前三个元素的和)
第四个位置是a[0][0]+a[0][1]+a[0][2]+a[0][3],
第五个位置是a[0][0]+a[1][0],
…
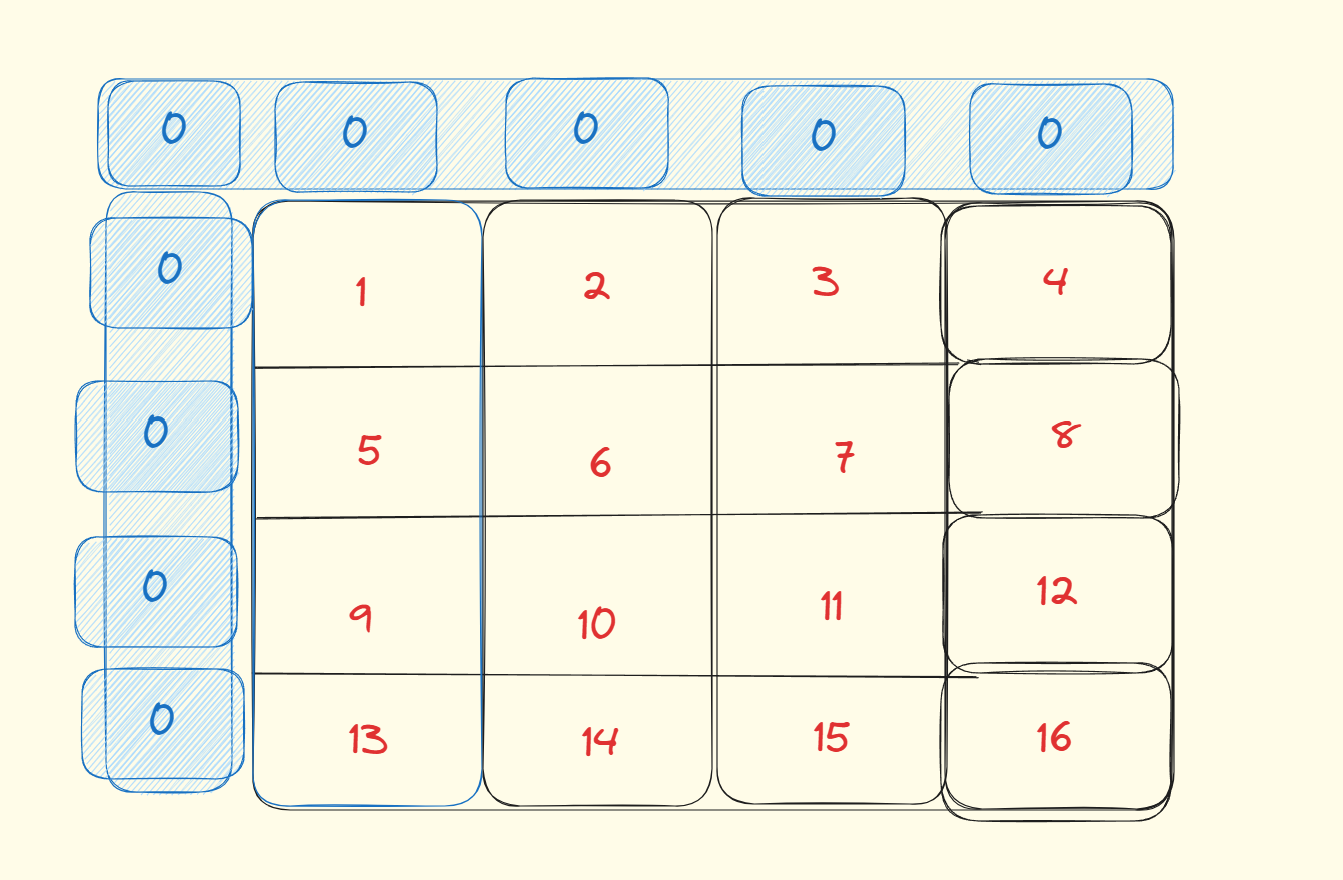
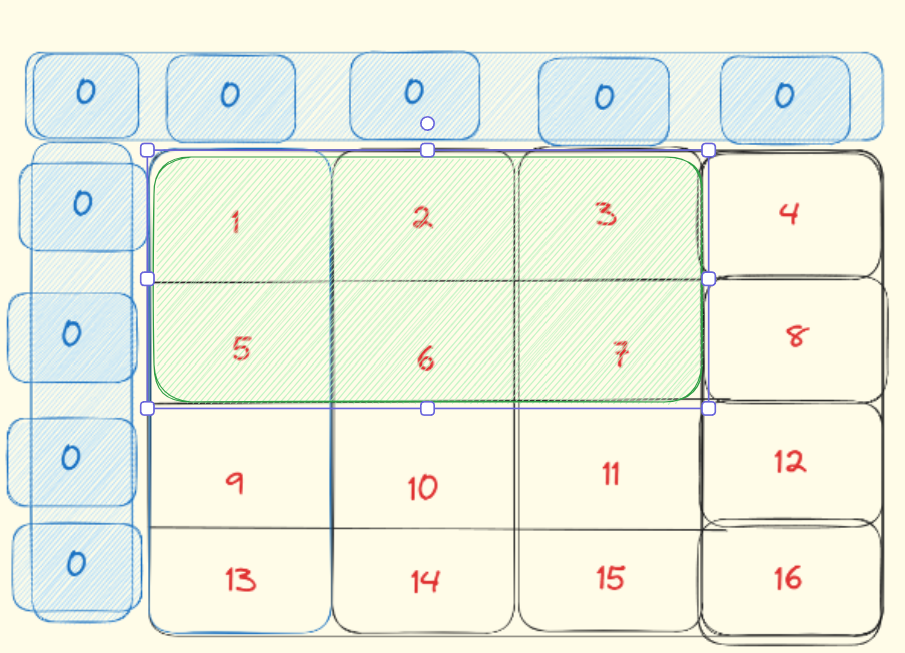
那么用java程序应该如何实现呢:
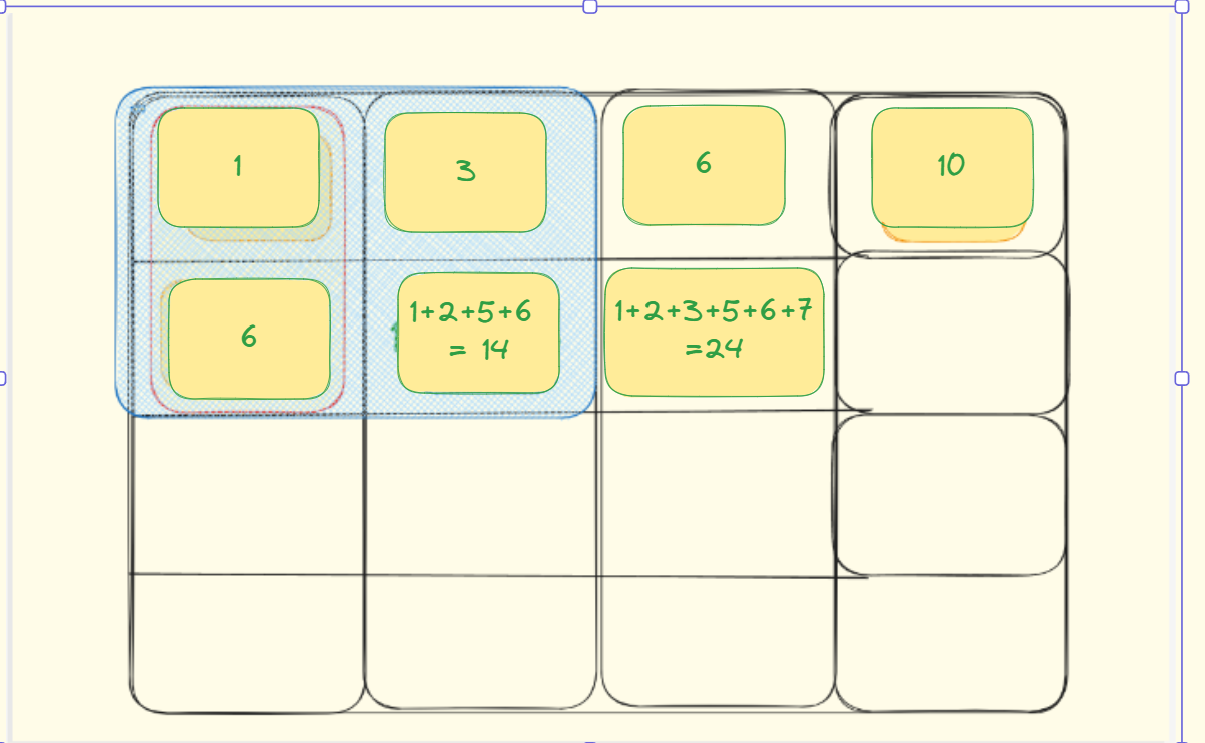
比如说:求值为7这个位置的和:1+2+3+5+6+7
可以分解为:三个红色的-一个重复的绿色
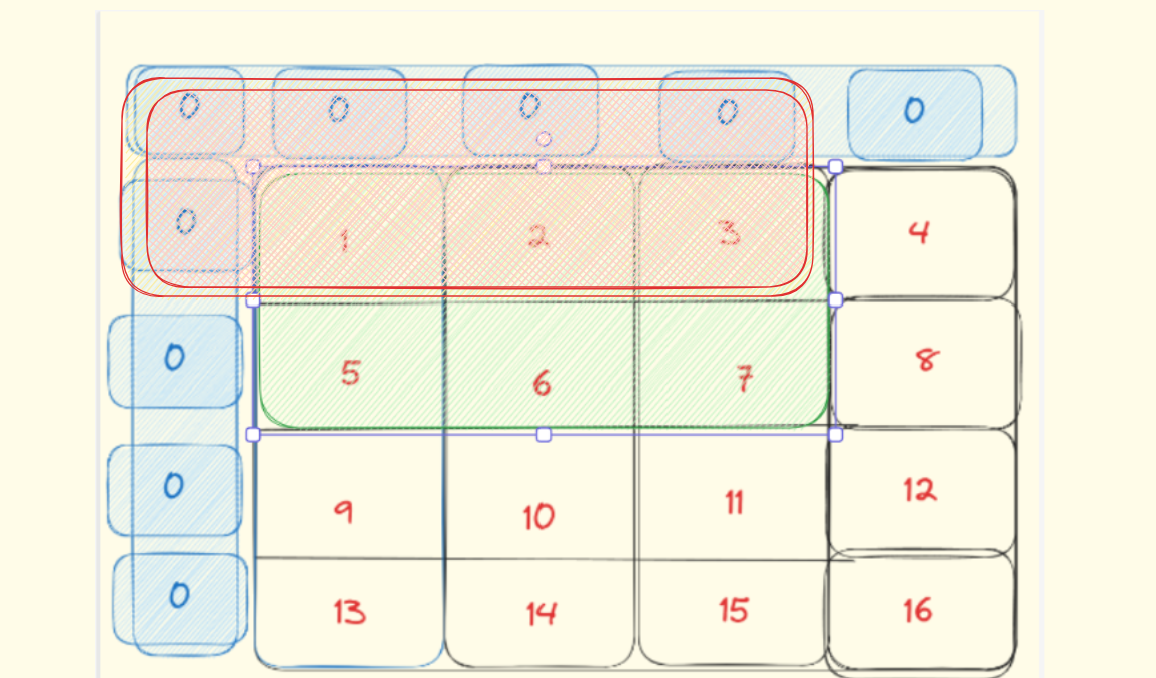
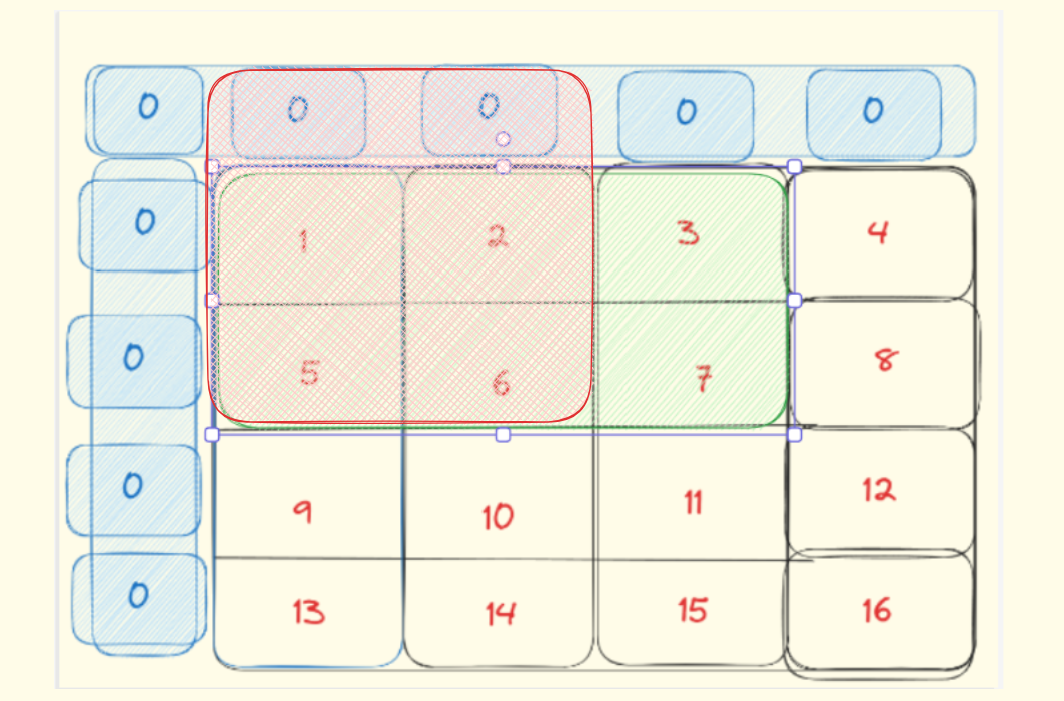
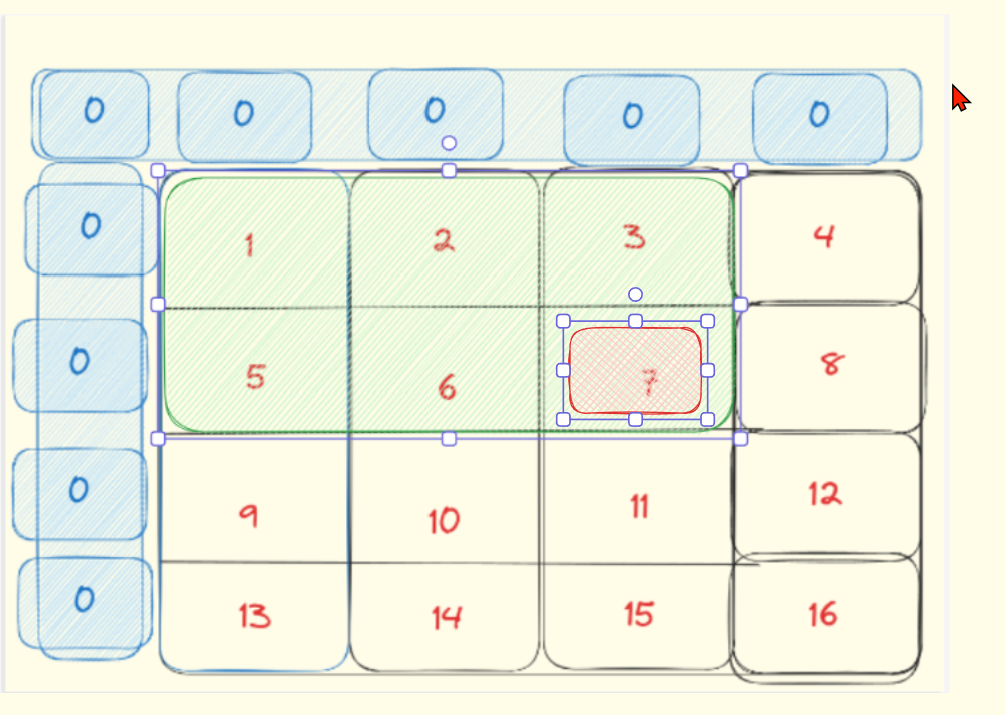
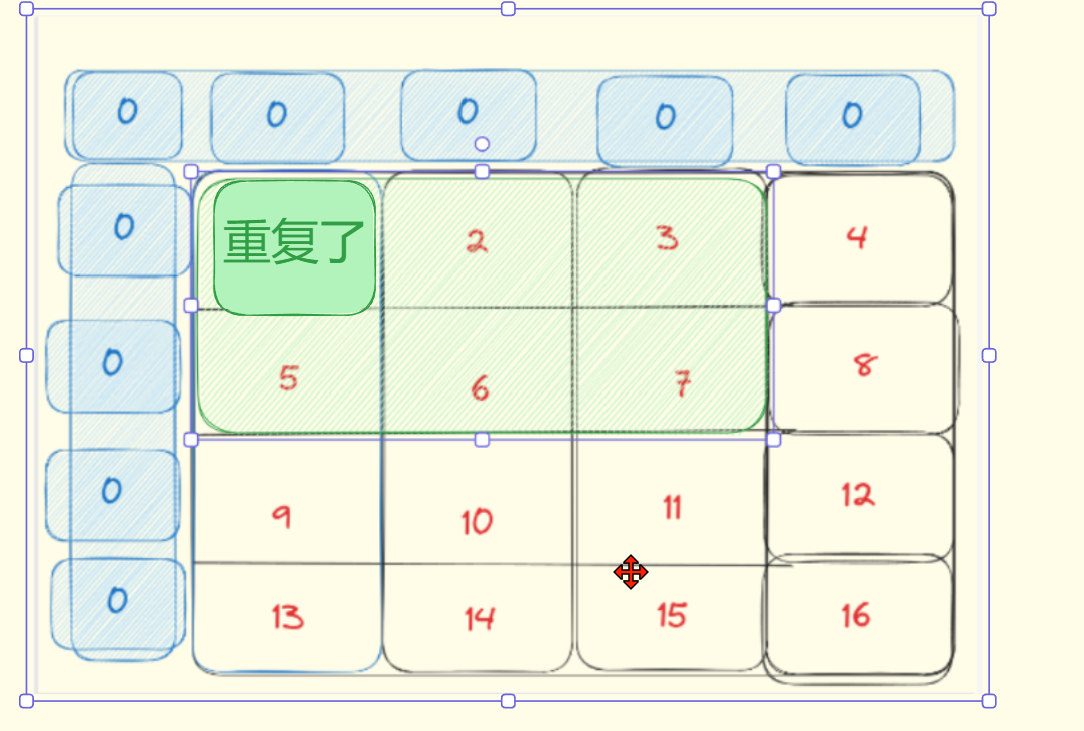
即: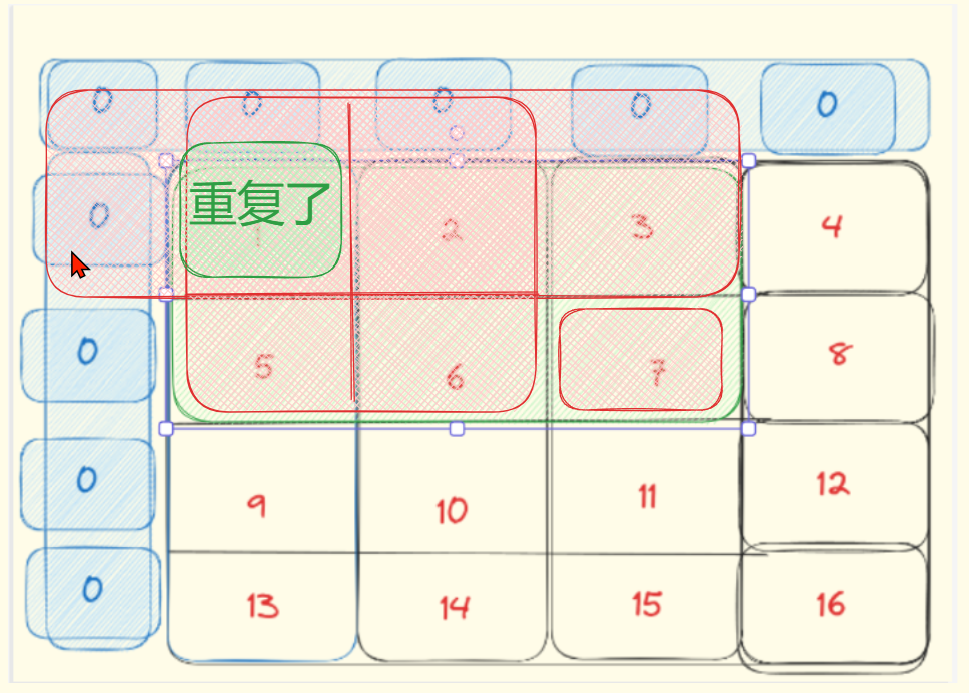
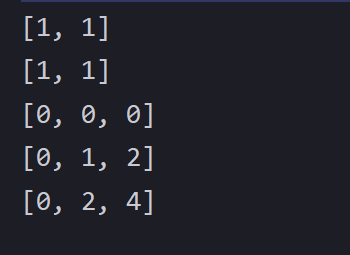
//初始化数组int [][] a=new int[2][2];for (int i = 0; i <a.length ; i++) {for (int j = 0; j <a[i].length ; j++) {a[i][j]=1;}System.out.println(Arrays.toString(a[i]));}//存储求和的数组int[][] sum=new int[a.length+1][a[0].length+1];//这里需要额外加一行+加一列for (int i = 1; i <sum.length ; i++) {for (int j = 1; j <sum.length ; j++) {//核心语句:sum[i][j]=sum[i][j-1]+sum[i-1][j]-sum[i-1][j-1]+a[i-1][j-1];//行成立的+列成立的-重合的+新增的}}//打印出结果for (int i = 0; i <sum.length ; i++) {System.out.println(Arrays.toString(sum[i]));}
相关文章:

求二维子数组的和(剖析)
文章目录 🐒个人主页🏅JavaSE系列专栏📖前言:本篇剖析一下二维子数组求和规则: 🐒个人主页 🏅JavaSE系列专栏 📖前言:本篇剖析一下二维子数组求和 规则: 这…...
代码开发思路介绍)
无(低)代码开发思路介绍
无代码或者低代码开发的思路,是通过非编程代码,而是基于页面拖拉拽的方式来实现创建web应用的功能。 作为程序员我们知道私有云公有云已经实现了基础设施的web方式管理。DEVOPS把代码发布,管理也实现了web方式管理。那么我们很容易能够想到,只要把拖拉拽出来的项目自动化部…...

代码随想录刷题 Day14
144.二叉树的前序遍历(opens new window) 要注意下创建函数参数传递不是很理解 class Solution { public:void tranversal(TreeNode* s, vector<int> &b) {if (s NULL) {return;}b.push_back(s->val);tranversal(s->left, b);tranversal(s->right, b);}v…...

二分类问题的解决利器:逻辑回归算法详解(一)
文章目录 🍋引言🍋逻辑回归的原理🍋逻辑回归的应用场景🍋逻辑回归的实现 🍋引言 逻辑回归是机器学习领域中一种重要的分类算法,它常用于解决二分类问题。无论是垃圾邮件过滤、疾病诊断还是客户流失预测&…...

docker alpine镜像中遇到 not found
1.问题: docker alpine镜像中遇到 sh: xxx: not found 例如 # monerod //注:此可执行文件已放到/usr/local/bin/ sh: monerod: not found2.原因 由于alpine镜像使用的是musl libc而不是gnu libc,/lib64/ 是不存在的。但他们是兼容的&…...

python的多线程多进程与多协程
python的多线程是假多线程,本质是交叉串行,并不是严格意义上的并行,或者可以这样说,不管怎么来python的多线程在同一时间有且只有一个线程在执行(举个例子,n个人抢一个座位,但是座位就这一个,不…...

一文介绍使用 JIT 认证后实时同步用户更加优雅
首先本次说的 JIT 指的是 Just In Time ,可以理解为及时录入,一般用在什么样的场景呢? 还记的上次我们说过关于第三方组织结构同步的功能实现,主要目的是将第三方源数据同步到内部平台中来,方便做管控和处理 此处的管…...

搞定“项目八怪”,你就是管理高手!
大家好,我是老原。 玛丽.弗列特说:“权力已经逐渐被视为一个群体的组合能力。我们通过有效联系获取力量。” 有效联系也就是指的沟通,这个部分占据我们项目经理工作内容的80%,可见沟通在项目管理中的重要性。 项目经理的沟通包…...
机器视觉-标定篇
3D结构光标定 结构光视觉的优点: 非接触、信息量大、测精度高、抗干扰能力强。 结构光视觉传感器参数的标定包括:摄像机参数标定、结构光平面参数标定。 结构光视觉测量原理图 我们不考虑镜头的畸变,将相机的成像模型简化为小孔成像模型…...

linux离线安装make
一、下载rpm包 https://pkgs.org/search/?qmake 二、拷贝至服务器 三、安装make rpm -ivh make-3.82-24.el7.x86_64.rpm四、查看是否安装成功 make -v...

【深度学习】卷积神经网络(LeNet)【文章重新修改中】
卷积神经网络 LeNet 前言LeNet 模型代码实现MINST代码分块解析1 构建 LeNet 网络结构2 加载数据集3 初始化模型和优化器4 训练模型5 训练完成 完整代码 Fashion-MINST代码分块解析1 构建 LeNet 网络结构2 初始化模型参数3 加载数据集4 定义损失函数和优化器5 训练模型 完整代码…...
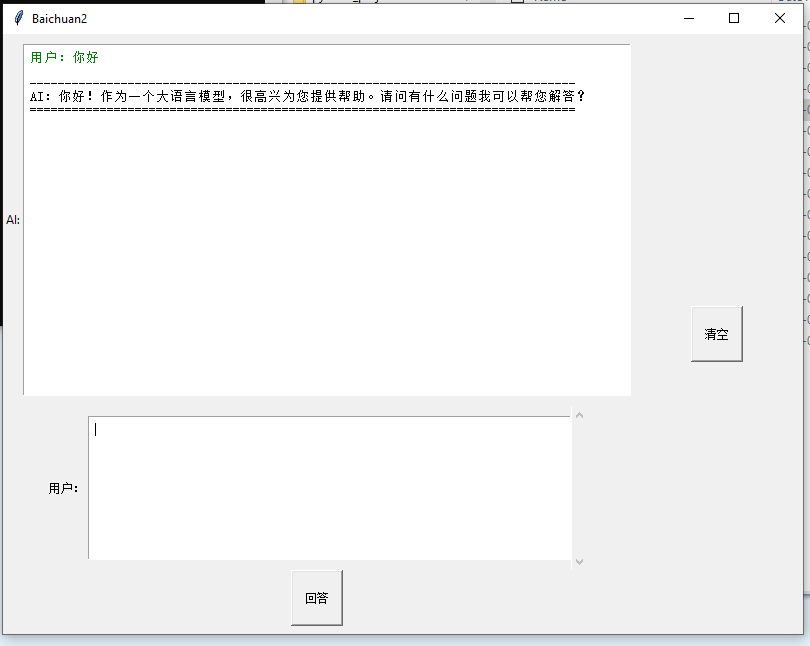
win10 Baichuan2-7B-Chat-4bits 上部署 百川2-7B-对话模型-4bits量化版
搞了两天才搞清楚跑通 好难呢,个人电脑 win10 ,6GB显存 个人感觉 生成速度很慢,数学能力不怎么行 没有ChatGLM2-6B 强,逻辑还行, 要求: 我的部署流程 1.下载模型 ,下载所有文件 然后 放到新建的model目录 https://huggingface.co/baichuan-inc/Baichuan2-7B-Chat-4bits/tr…...
2023/9/20总结
maven maven本质是 一个项目管理工具 将项目开发 和 管理过程 抽象成 一个项目对象模型(POM) POM (Project Object Model) 项目对象模型 作用 项目构建 提供标准的自动化 项目构建 方式依赖管理 方便快捷的管理项目依赖的资源…...

【Git】git 分支或指定文件回退到指定版本
目录 一、分支回滚 1. 使用 git reset 命令 2.使用 git revert 命令 3.使用 git checkout 命令 二、某个文件回滚 1.查看哪些文件发生修改 2.然后查看提交记录(最近几次提交) 3.执行提交命令 一、分支回滚 1. 使用 git reset 命令 命令可以将当前分支的 HEAD 指针指向指…...
Java 消息策略的实现 - Kafak 是怎么设计的
这个也是开放讨论题,主要讨论下 Kafka 在消息中是如何进行实现的。 1_cCyPNzf95ygMFUgsrleHtw976506 21.4 KB 总结 这个题目的开发性太强了。 Kafka 可以用的地方非常多,我经历过的项目有 Kafka 用在消息处理策略上的。这个主要是 IoT 项目,…...
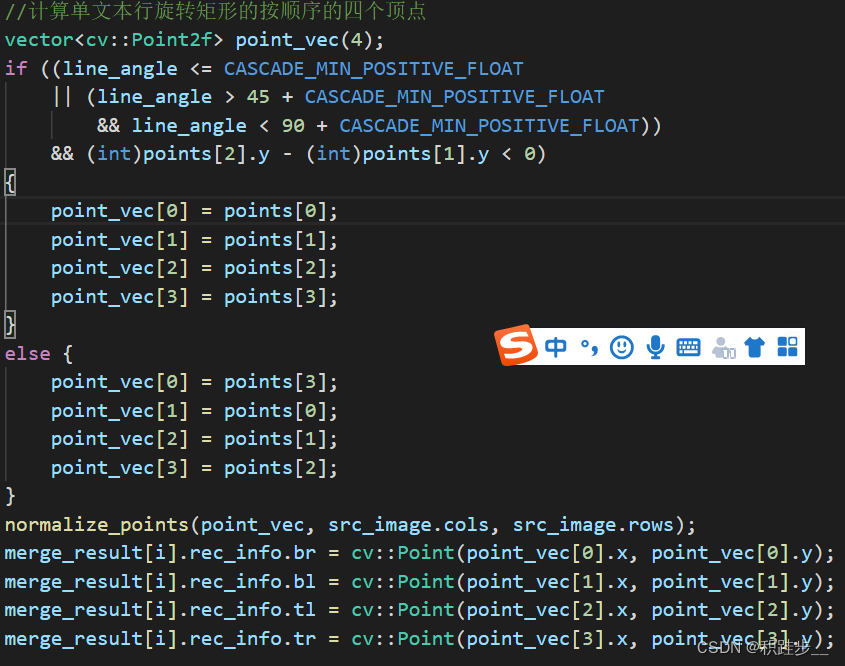
c++opencv RotatedRect 旋转矩形角度转换和顶点顺序转换
这里写自定义目录标题 以下代码记录主要是完成轮廓点求解最小外接矩形之后计算该文本行的角度和旋转矩形的左下(bl),左上(tl),右上(tr),右下(br)的坐标点。 RotatedRect rtminAreaRect(contours…...
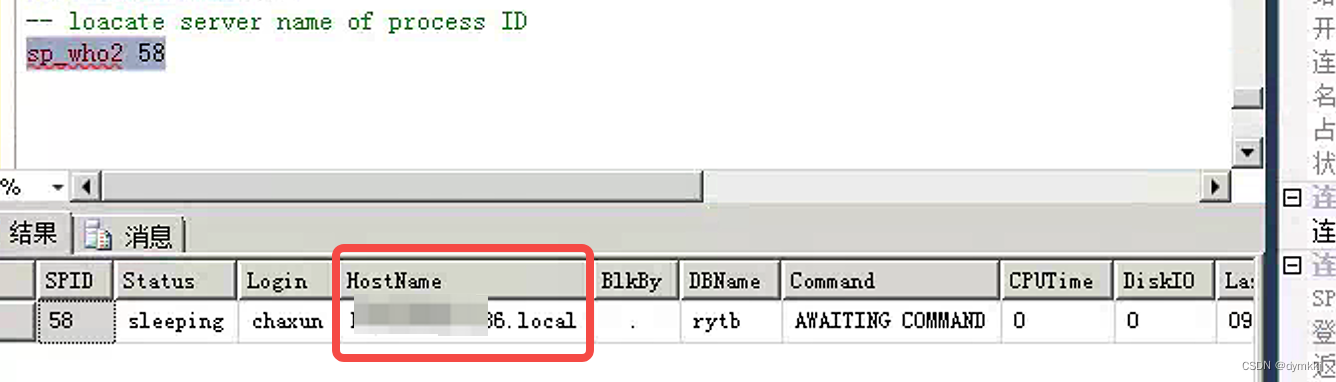
Flink-CDC 抽取SQLServer问题总结
Flink-CDC 抽取SQLServer问题总结 背景 flink-cdc 抽取数据到kafka 中,使用flink-sql进行开发,相关问题总结flink-cdc 配置SQLServer cdc参数 1.创建CDC 使用的角色, 并授权给其查询待采集数据数据库 -- a.创建角色 create role flink_role;-- b.授权…...
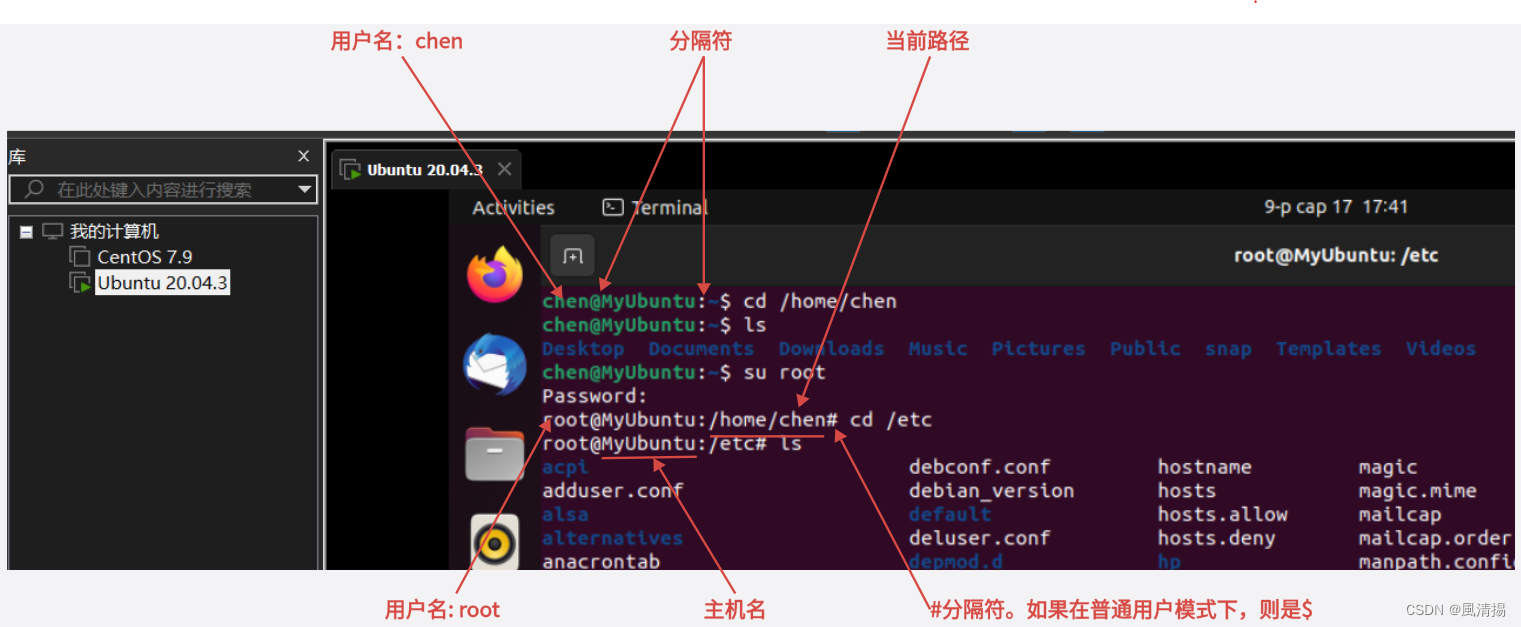
Linux 系统目录结构 终端
系统目录结构 Linux 或 Unix 操作系统中,所有文件和目录呈一个以根节点为始的倒置的树状结构。文件系统的最顶层是根目录,用 / 来表示根目录。在根目录之下的既可以是目录,也可以是文件,而每一个目录中又可以包含子目录文件。如此…...

Layui + Flask | 实现注册、登录功能(案例篇)(08)
此案例内容比较多,建议滑到最后点击阅读原文,阅读体验更佳。后续也会录制案例视频,将在本周内上传到同名的 b 站账号。 已经看了 layui 表单相关的知识,接下来就可以实现注册功能,功能逻辑如下: 项目创建 新建 flask 项目下载 layui 文件,解压之后复制到指定文件编写前…...

GitLab数据迁移后出现500错误
一、背景 去年做GitLab数据迁移时,写过一篇文章《GitLab的备份与还原》。后来发现新创建的项目没问题,但对于迁移过来的项目,修改名称等信息,或者删除该项目时,会出现500错误,以为是系统问题&#…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...
