切换分支报错：Untracked Files Prevent Checkout
切换分支报错：Untracked Files Prevent Checkout
- git分支切换 Untracked Files Prevent Checkout
- 本人解决办法：
git分支切换 Untracked Files Prevent Checkout
新起的项目在切换master分支到工作分支时，出现下图的问题：
Untracked Files Prevent Checkout
Move or commit them before checkout
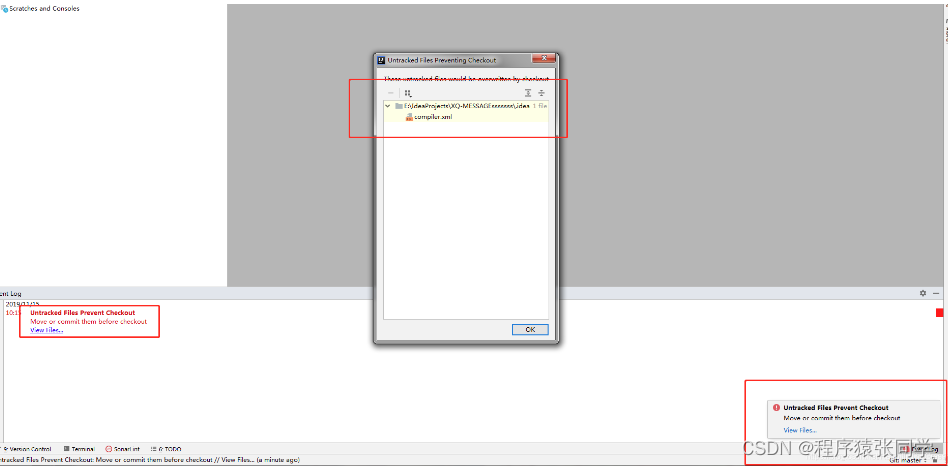
网上的解决办法：
大多都是执行git clean -f ，将所有untracked file 一次性删除。
本人发现执行该命令后会把项目的文件删掉，难以达到预期效果。
本人解决办法：
- 进入工程所在目录
- 右键打开Git Bash Here
- 执行git checkout -f master（master是我想切换的分支）
这样再回到IDEA会发现分支已经切换过去了。
相关文章：
切换分支报错：Untracked Files Prevent Checkout
切换分支报错：Untracked Files Prevent Checkoutgit分支切换 Untracked Files Prevent Checkout本人解决办法：git分支切换 Untracked Files Prevent Checkout 新起的项目在切换master分支到工作分支时，出现下图的问题： Untracked…...
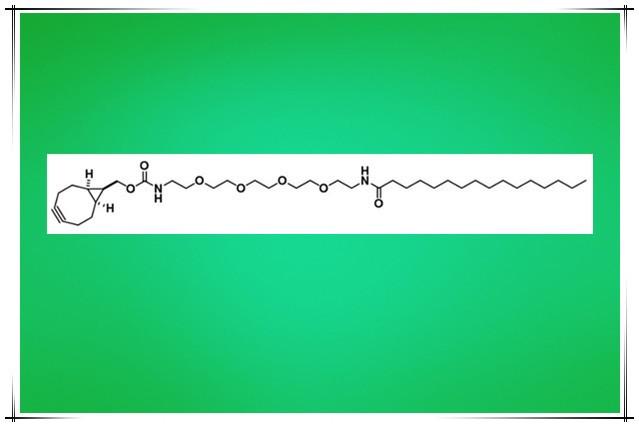
endo-BCN-PEG4-Palmitic，环丙烷环辛炔四聚乙二醇-Palmitic包装灵活
endo-BCN-PEG4-Palmitic，endo环丙烷环辛炔四聚乙二醇-Palmitic反应特点：endo-BCN-PEG4-Palmitic 酯在其末端含有一个 Palmitic基和一个 BCN 基。对点击试剂来说同样会通过不同的小分子PEG进行连接，BCN-PEG-acid、BCN-PEG-NHS ester、BCN-PEG-…...
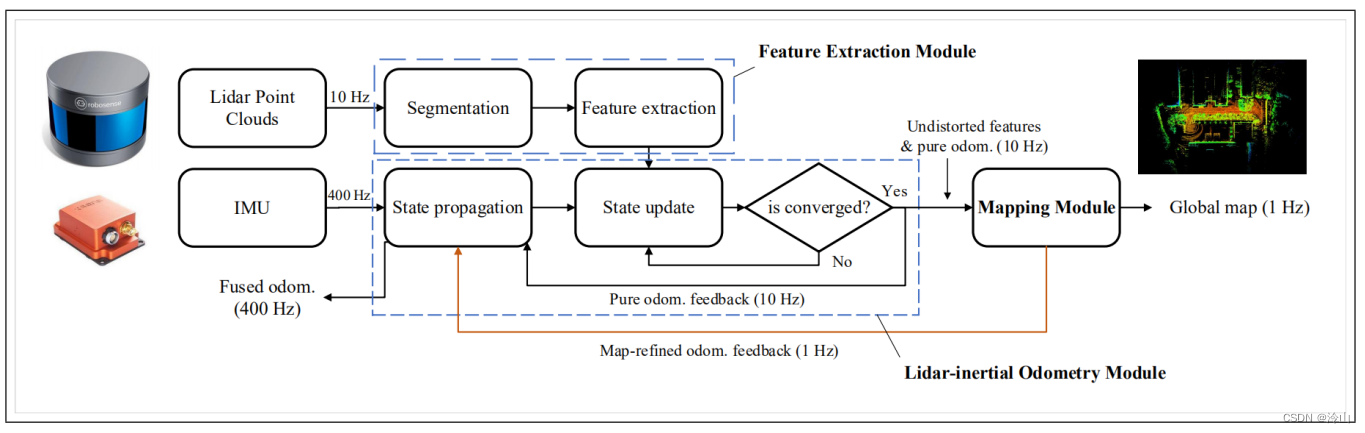
多传感器融合定位十一-基于滤波的融合方法Ⅱ
多传感器融合定位十一-基于滤波的融合方法Ⅱ1. 编码器运动模型及标定1.1 编码器基础知识1.2 编码器运动模型1.2.1 旋转半径求解1.2.2 角速度求解1.2.3 线速度求解1.2.4 位姿求解1.3 编码器的标定1.3.1 轮子半径标定1.3.2 轮子与底盘中心距离标定2. 融合编码器的滤波方法2.1 核心…...
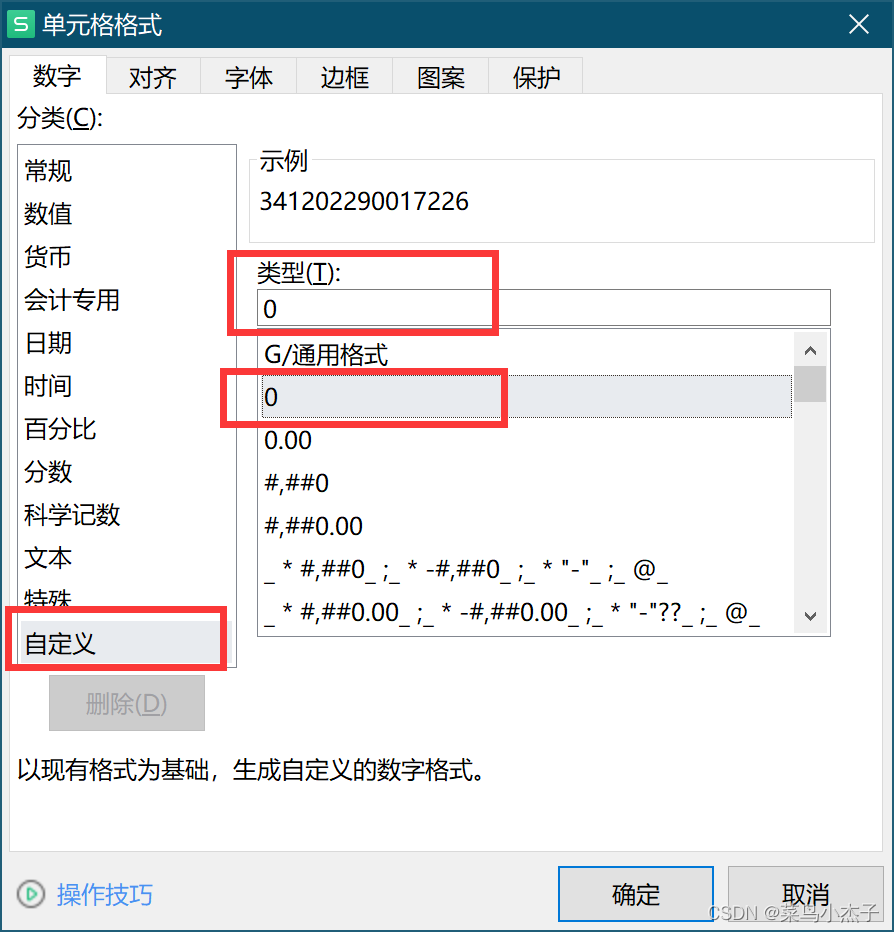
JAVA使用poi解析execl解决数值被转为科学计数法（如：手机号、身份证号、电话、等）解决方法
1、原由 大家都知道数字在EXCEL表格中存储时有两种表现形式。1.数字作为数值存储。当数字作为数值存储时，单元格中的数字可以参与数学运算。2.数字作为文本存储。当数字作为文本存储时,单元格中的数值不能够参与数学运算。 数字作为文本存储时，如果没有更…...
的使用)
hive中substring_index()的使用
substring_index(str,delim,count)str:要处理的字符串delim:分隔符count:计数例子：strwww.wikibt.comsubstring_index(str,.,1)结果是：wwwsubstring_index(str,.,2)结果是：www.wikibt如果count是正数，那么就是从左往右数ÿ…...
LocalDateTime设置时间的年、月、日、时、分、秒、纳秒
如何把String/Date转成LocalDateTime参考String、Date与LocalDate、LocalTime、LocalDateTime之间互转 String、Date、LocalDateTime、Calendar与时间戳之间互相转化参考String、Date、LocalDateTime、Calendar与时间戳之间互相转化 方法介绍 withYear(int year) 指定日期的…...
C语言rand和srand用法详解
在实际编程中，我们经常需要生成随机数，例如，贪吃蛇游戏中在随机的位置出现食物，扑克牌游戏中随机发牌。在C语言中，我们一般使用 <stdlib.h> 头文件中的 rand() 函数来生成随机数，它的用法为ÿ…...
安装作业
1、安装方法 mysql安装常见的方法有四种 序号安装方式说明1yum\rpm简单、快速，不能定制参数2二进制解压，简单配置就可使用 免安装 mysql-a.b.c-linux2.x-x86_64.tar.gz3源码编译可以定制参数，安装时间长 mysql-a.b.c.tar.gz4源码制成rpm包把…...
电压放大器在非共线混频方法检测混凝土中的应用
实验名称：电压放大器在非共线混频方法检测混凝土中的应用研究方向：无损检测测试目的：无损检测是在不损伤或不干扰待测物体的结构材料的情况下，对其内部损伤进行探测的方法。传统无损检测法在仪器携带，操作程序…...
二十四、Gtk4-GtkExpression
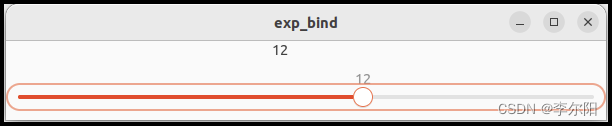
GtkExpression是一种基本类型。它不是GObject的后代。GtkExpression提供了一种描述对值的引用的方法。GtkExpression需要求值才能获得值。 它类似于算术计算。 1 2 3 12是一个表达式。给出了计算的方法。3是来自表达式的值。求值是计算表达式并得到值。 GtkExpression是一种…...
Oracle Dataguard（主库为 Oracle rac 集群）配置教程（02）—— Oracle RAC 主库的相关操作
Oracle Dataguard（主库为 Oracle rac 集群）配置教程（02）—— Oracle RAC 主库的相关操作 / 本专栏详细讲解 Oracle Dataguard（Oracle 版本为11g，主库为双节点 Oracle rac 集群）的配置过程。主要…...
midjournery AI绘画使用指南
midjournery AI绘画使用指南 基于Discord的Midjournery配置： https://www.bilibili.com/video/BV16d4y1A7Zq/?spm_id_from333.337.search-card.all.click&vd_source9c3ca9555620bed64bdee27ae49d37cf 使用原则 使用midjournery绘画的原则是给出对脑海中某个…...
iptables防火墙SNAT和DNAT
iptables防火墙SNAT和DNAT一、SNAT原理和应用1、SNAT原理2、SNAT应用环境3、SNAT转换前提条件二、SNAT案列1、实验需求2、实验环境3、实验目的三、DNAT原理和应用1、DNAT原理2、DNAT 应用环境3、DNAT转换的前提条件四、DNAT案列总结一、SNAT原理和应用 1、SNAT原理 SNAT原理:…...
python | 第二章考试题和练习题
一、考试题 1、turtle八边形绘制 问题描述： 使用turtle库，绘制一个八边形。 参考代码： import turtle as t t.pensize(2) for i in range(8):t.fd(100)t.left(45) 2、turtle八角图形绘制 问题描述： 使用turtle库，…...
Mysql 存储引擎设计：xa协议相关接口功能及实现
需要对接的接口以及每个接口的实现 recovery 阶段 此阶段由 xa.cc 文件中的 xarecover_handlerton() 函数完成，它通过三个接口实现与存储引擎的沟通：recover()，commit_by_xid() ，rollback_by_xid()。其流程如下： 此…...
字符串常量池
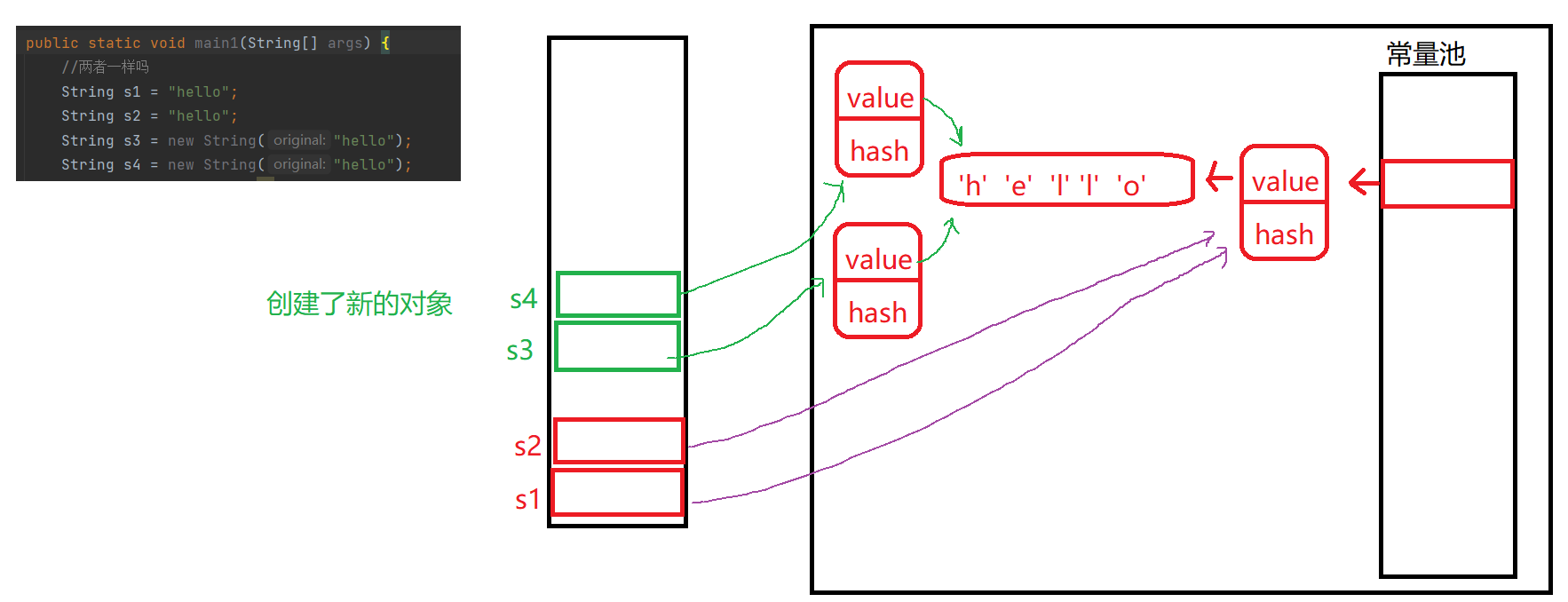
1.创建对象的思考下面两种创建字符串的方式一样吗？public static void main(String[] args) {//两者一样吗String s1 "hello";String s2 "hello";String s3 new String("hello");String s4 new String("hello");System…...
让技术更有温度，腾讯Light 点亮公益之光
蓝天白云，远处是广东最长跨海大桥——南澳大桥，一艘小船在海面驶过，近处一头中华白海豚露出水面。在第三届腾讯Light技术公益创造营上，海南智渔可持续发展研究中心科学总监郑锐强为我们展现这样一幅人与自然和平相处的美好画面。随…...
电子采购一体化解决方案
企事业数字化转型专家，提供各类应用解决方案。您身边的赋能小助手！ 文章目录前言一、当下采购的痛点二、解决方案-供应商管理1.供应商管理三、解决方案-企业询价、供应商报价管理四、解决方案-采购订单五、送货、到货、订单管理总结前言 随着各类产业链…...
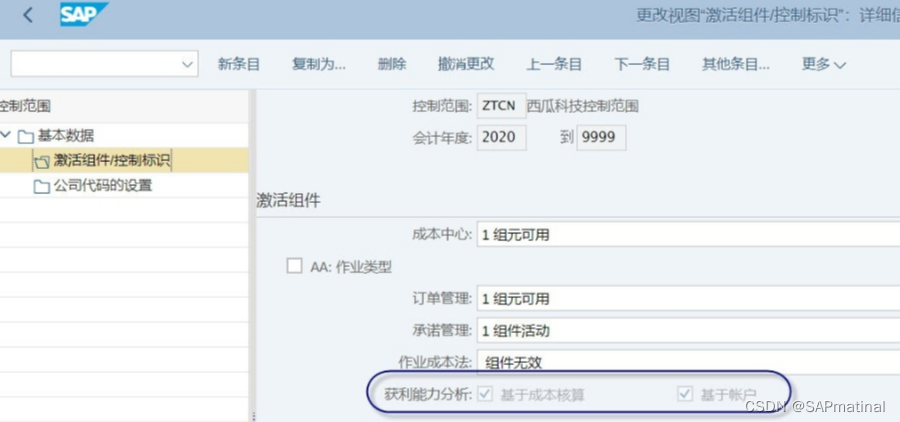
SAP COPA 获利能力分析深度解析
一、获利分析配置及相关值概述 二、配置：组织结构 2.1 定义经营范围-KEP8 2.2 维护经营关注点-KEA0 2.3 获利能力分析类型解析 2.4 控制范围分配给经营范围-KEKK 三、配置：数据结构-KEA0 3.1 特征字段 3.1.1 特征字段类别 3.1.2 维护特征字段-K…...
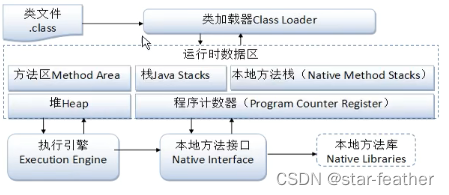
Java学习记录day6
书接上回 类与对象 static关键字 static的作用： 修饰一个属性：声明为static的变量实质上就是一个全局变量,其生命周期为从类被加载开始一直到程序结束；修饰方法：无须本类的对象也可以调用该方法；修饰一个类&#x…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学（Elliptic Curve Cryptography）是基于椭圆曲线数学理论的公钥密码系统，由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA，ECC在相同安全强度下密钥更短（256位ECC ≈ 3072位RSA…...
Appium+python自动化（十六）- ADB命令
简介 Android 调试桥(adb)是多种用途的工具，该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具，其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利，如安装和调试…...
FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下，无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作，还是游戏直播的画面实时传输，低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架，凭借其灵活的编解码、数据…...
【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍，多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解（初学者版） 1. static（默认值） 2. relative（相对定位） 3. absolute（绝对定位） 4. fixed（固定定位） 5. sticky（粘性定位） 三、定位元素的层级关系（z-i…...
Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作（核心）三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结，涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...
【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索（基于物理空间 广播范围）2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展，人们对手机的需求越来越大，各种手机软件也都在被广泛应用，但是对于手机进行数据信息管理，对于手机的各种软件也是备受用户的喜爱，社区养老保险系统小程序被用户普遍使用，为方…...
JVM 内存结构 详解
内存结构 运行时数据区： Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器： 线程私有，程序控制流的指示器，分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...
排序算法总结（C++）
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指：同样大小的样本 **（同样大小的数据）**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...
掌握 HTTP 请求：理解 cURL GET 语法
cURL 是一个强大的命令行工具，用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中，cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...