蓝桥杯算法训练合集十三 1.P06022.P07033.逗志芃的危机4.唯一的小可爱5.JOE的矩阵
目录
1.P0602
2.P0703
3.逗志芃的危机
4.唯一的傻子
5.JOE的矩阵
1.P0602
问题描述
编写一个程序,输入一个4位的自然数,将组成该数的各位数字重新排列,形成一个最大数和一个最小数,之后用最大数减去最小数,得到一个新的自然数,把这个数打印出来。然后对于这个新的自然数,重复上述步骤,直到该自然数的值不再发生变化。例如,假设用户输入的自然数为1001,那么由它所形成的最大数为1100,最小数为11,因此新的自然数为1089。对于1089,由它形成的最大数为9810,最小数为189,因此新的自然数为9621。9621的最大数为9621,最小数为1269,结果为8352,。8352的最大数为8532,最小数为2358,结果为6174。6174的最大数为7641,最小数为1467,结果仍为6174,因此程序结束。
样例输入
1001
样例输出
6174
示例代码
#include<iostream>
#include<algorithm>
using namespace std;int main() {int n, a[4];cin >> n;int max, min;while (1) {int temp = 1000,n1=n;for (int i = 0; i < 4; i++) {//找到每个位上的数a[i] = n / temp;n -= a[i] * temp;temp /= 10;}sort(a, a + 4);//从小到大排序min = a[0] * 1000 + a[1] * 100 + a[2] * 10 + a[3] * 1;max = a[0] * 1 + a[1] * 10 + a[2] * 100 + a[3] * 1000;if (max - min == n1) {//如果符合题目要求cout << n1;return 0;}n = max - min;//否则继续循环}return 0;
}2.P0703
问题描述
一个整数的反置数指的是把该整数的每一位数字的顺序颠倒过来所得到的另一个整数。如果一个整数的末尾是以0结尾,那么在它的反置数当中,这些0就被省略掉了。比如说,1245的反置数5421,而1200的反置数是21。请编写一个程序,输入两个整数,然后计算这两个整数的反置数之和sum,然后再把sum的反置数打印出来。例如,如果用户输入:435和754,则输出结果为199。要求:由于在本题中需要多次去计算一个整数的反置数,因此必须把这部分代码抽象为一个函数的形式。
样例输入
435 754
样例输出
199
示例代码
#include<iostream>
#include<algorithm>
using namespace std;
int find_count(int n) {//求出n是几位数int cnt=0;int temp = 1;for (int i = 0;; i++) {//从10的0次方开始if (n / temp == 0) {cnt = i;break;}temp *= 10;}return cnt;
}
int fanzhi(int n) {int temp = 1,temp1,cnt=0,index[12] = { 0 };cnt = find_count(n);for (int i = 1; i < cnt; i++) {//最高位的10次方值temp *= 10;}temp1 = temp;for (int i = 0; i < cnt; i++) {//分解每个位置上的数index[i] = n/ temp;n = n - index[i] * temp;temp /= 10;}n = 0;for (int i = cnt - 1; i >= 0; i--) {//倒序n += index[i] * temp1;temp1 /= 10;}//cout <<cnt<<" "<< n << endl;return n;
}
int main() {int a, b,sum;cin >> a >> b;sum = fanzhi(a) + fanzhi(b);sum = fanzhi(sum);cout << sum;return 0;
}3.逗志芃的危机
问题描述
逗志芃又一次面临了危机。逗志芃的妹子是个聪明绝顶的人,相比之下逗志芃就很菜了。现在她妹子要和他玩一个游戏,这个游戏是这样的:一共有n个数(n是偶数)写成一行,然后两个人轮流取数,每次只能从最前面或者最后面取走一个数,全部取完则游戏结束,之后每个人取走的数的和就是每个人的得分。由于逗志芃妹子很厉害,但他又不想输,所以只能找到你了,你要告诉他最多可以得到多少分。(注意,妹子智商是maxlongint所以是不会犯错的,每次的策略必然最优,而且逗志芃是先手)
输入格式
第一行一个数n,表示有n个数。
第二行就是进行游戏的n个数。
输出格式
一个数,最高得分
样例输入
2
10 20
样例输出
20
数据规模和约定
例:0<n,m<=1000,每个数不超过10000 。
示例代码
#include<iostream>
using namespace std;int max(int a, int b) {if (a > b) {return a;}else {return b;}
}
int min(int a, int b) {if (a > b) {return b;}else {return a;}
}
int a[1000], res[1000][1000];//res[l][r]表示l到r区间里逗哥所能取的最大和int main() {int n,sum=0;cin >> n;for (int i = 0; i < n; i++) {cin >> a[i];}for (int r = 0; r < n; r++) {for (int l = r; l >= 0; l--) {if (l == r) {//妹妹选,而且是最后一个数,她没得选res[l][r] = 0;}else if ((r - l) % 2 == 1) {//我们选择,尽可能大res[l][r] = max(res[l + 1][r] + a[l], res[l][r - 1] + a[r]);}else {//妹妹选,她更大,也就是尽量让我们小res[l][r] = min(res[l + 1][r], res[l][r - 1]);}}}cout <<res[0][n-1];return 0;
}4.唯一的傻子
问题描述
腿铮找2255有点事,但2255太丑了,所以腿铮不知道他的长相。正愁不知道到如何找他的时候,他突然看见计33班围成了一个圈在领微积分试卷。计33班有n个人,其中班长编号为0,其余同学依次按顺时针方向编号。
只听见计33小导说“x号同学顺时针方向往后数的第k个的神犇出列(不包括x号同学),领取满分试卷!”。剩下的人继续围成一个小圈。这样一个过程持续了n-1次,那么显然,最后只剩下了一个人。众所周知,2255是个大傻子,门门挂科,不符合满分试卷这一前提条件。通过这样一个过程,腿铮终于找到了2255并血虐了他。
求2255的编号是多少。
输入格式
第一行一个n,表示计33班的人数。
接下来n-1行,表示小导说话中的x和k。
输出格式
一个数字,表示2255的编号。
样例输入
3
1 1
0 1
样例输出
0
数据规模和约定
前90%数据保证n<=10^4.
前100%数据保证n<=10^6,1<=k<min(当时圈中人数,1000)
示例代码
1.链表,最后一个超时了
#include<iostream>
#include<malloc.h>
using namespace std;typedef struct stu {int number;//学生编号struct stu *next;
}STU;void link_creat_head(STU** p_head, STU* p_new)
{STU* p_mov = *p_head;if (*p_head == NULL) //当第一次加入链表为空时,head执行p_new{*p_head = p_new;p_new->next = NULL;}else //第二次及以后加入链表{while (p_mov->next != NULL){p_mov = p_mov->next; //找到原有链表的最后一个节点}p_mov->next = p_new; //将新申请的节点加入链表p_new->next = NULL;}
}int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);STU* head = NULL, * p_new = NULL;int n;scanf("%d", &n);for (int i = 0; i < n; i++) {p_new = (STU*)malloc(sizeof(STU));//申请一个新节点p_new->number = i;link_creat_head(&head, p_new); //将新节点加入链表}int start, k;for (int i = 0; i < n - 1; i++) {scanf("%d %d", &start, &k);p_new = head;while (p_new->number != start) {//找到编号为start的学生p_new = p_new->next;}for (int j = 0; j < k-1; j++) {//找到这个学生,这个学生的下一个学生会被删除if (p_new->next == NULL) {//如果这个学生是链表尾部,那么该学生下一个为队首p_new = head;continue;}p_new = p_new->next;}if (p_new->next == NULL) {//如果要删除的学生为空,说明是删除的是队首,则要更新队首head = head->next;}else {p_new->next = p_new->next->next;}}printf("%d",head->number);return 0;
}2.逻辑分析(简单法)
当输入第n-1个时,还剩两个学生,要删除的肯定不是输入的那个学生,则最后一个输入的学生就是仅存下来的学生
#include<iostream>
using namespace std;int main(){int n;cin>>n;int x,k;for(int i=0;i<n-1;i++){scanf("%d%d", &x,&k);}cout<<x<<endl;return 0;
}5.JOE的矩阵
问题描述
最近JOE又在线性代数的模拟考中拿满分了,这直接导致了JOE对于计算矩阵的热情急剧下降,所以JOE希望能有这样一个程序能帮助他计算矩阵的秩。
输入格式
第一行,两个数n,m,表示矩阵是n*m的。
下面共n行,每行m个数(可能为负),表示这个矩阵。
输出格式
这个矩阵的秩。
样例输入
2 3
1 2 1
2 4 3
样例输出
2
数据规模和约定
40% n, m <= 5
70% n, m <= 10
100% n, m <= 20
分析
用寻找非零子式的方法确定矩阵的秩有其局限性,当矩阵阶数较高时,计算量会显著增加,因此在线性代数中使用初等变换化行阶梯型,是常用的方法。
示例代码
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>using namespace std;const int N = 110;
const double eps = 1e-8;double a[N][N];
int n, m;int gauss() {int r, c;for (r = 0, c = 0; c < n; c++) {//对第c列进行处理,则要将第c行包括之后的行进行处理// 找到最大值的行int t = r;for (int i = r; i < n; i++) {if (fabs(a[i][c]) > fabs(a[t][c]))t = i;}if (fabs(a[t][c]) < eps) continue;//如果最大的都是0,则该列以及对应的行不需要处理了// 2. 交换到对应的列的首行for (int i = c; i < m; i++) swap(a[r][i], a[t][i]);// 3. 本行首列置为1for (int i = m - 1; i >= c; i--) a[r][i] /= a[r][c];// 4. 下面的行首列置为0for (int i = r + 1; i < n; i++) {if (fabs(a[i][c]) < eps) continue;for (int j = m - 1; j >= c; j--) {a[i][j] -= a[i][c] * a[r][j]; // - 首航本列 * i, r首列商}}r++;}return r;
}int main() {cin >> n >> m;for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {scanf("%lf", &a[i][j]);// printf("%.2lf\n", a[i][j]);}}int t = gauss();printf("%d\n", t);return 0;
}
蓝桥杯算法训练-JOE的矩阵_天下一般的博客-CSDN博客
相关文章:

蓝桥杯算法训练合集十三 1.P06022.P07033.逗志芃的危机4.唯一的小可爱5.JOE的矩阵
目录 1.P0602 2.P0703 3.逗志芃的危机 4.唯一的傻子 5.JOE的矩阵 1.P0602 问题描述 编写一个程序,输入一个4位的自然数,将组成该数的各位数字重新排列,形成一个最大数和一个最小数,之后用最大数减去最小数,得到一…...
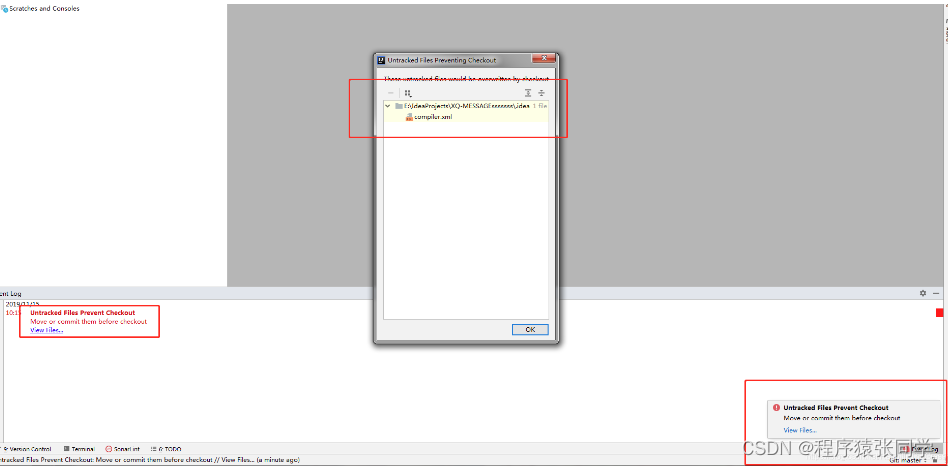
切换分支报错:Untracked Files Prevent Checkout
切换分支报错:Untracked Files Prevent Checkoutgit分支切换 Untracked Files Prevent Checkout本人解决办法:git分支切换 Untracked Files Prevent Checkout 新起的项目在切换master分支到工作分支时,出现下图的问题: Untracked…...
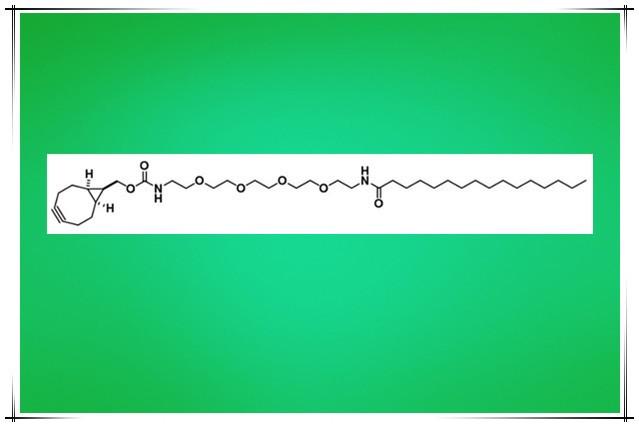
endo-BCN-PEG4-Palmitic,环丙烷环辛炔四聚乙二醇-Palmitic包装灵活
endo-BCN-PEG4-Palmitic,endo环丙烷环辛炔四聚乙二醇-Palmitic反应特点:endo-BCN-PEG4-Palmitic 酯在其末端含有一个 Palmitic基和一个 BCN 基。对点击试剂来说同样会通过不同的小分子PEG进行连接,BCN-PEG-acid、BCN-PEG-NHS ester、BCN-PEG-…...
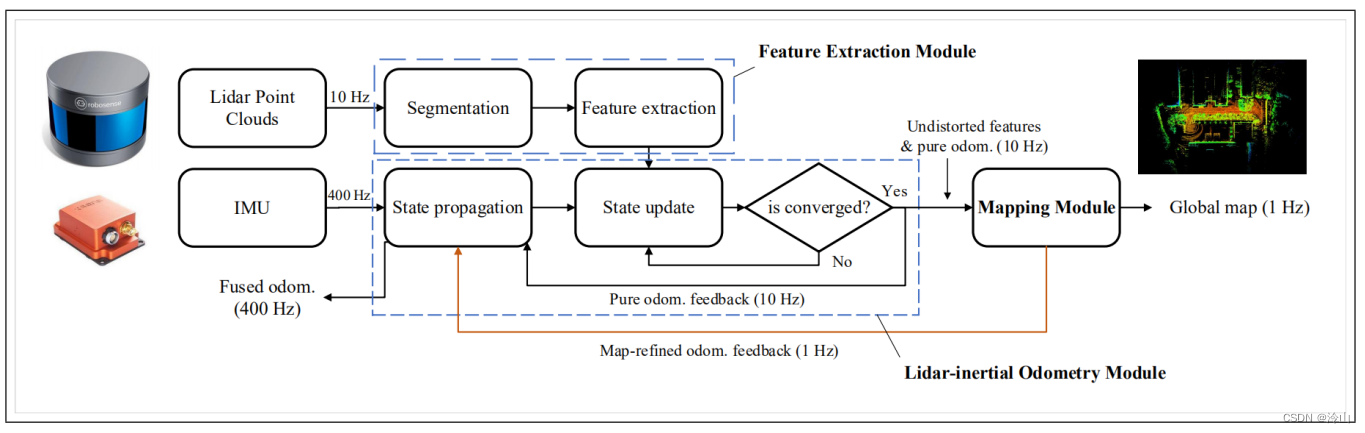
多传感器融合定位十一-基于滤波的融合方法Ⅱ
多传感器融合定位十一-基于滤波的融合方法Ⅱ1. 编码器运动模型及标定1.1 编码器基础知识1.2 编码器运动模型1.2.1 旋转半径求解1.2.2 角速度求解1.2.3 线速度求解1.2.4 位姿求解1.3 编码器的标定1.3.1 轮子半径标定1.3.2 轮子与底盘中心距离标定2. 融合编码器的滤波方法2.1 核心…...
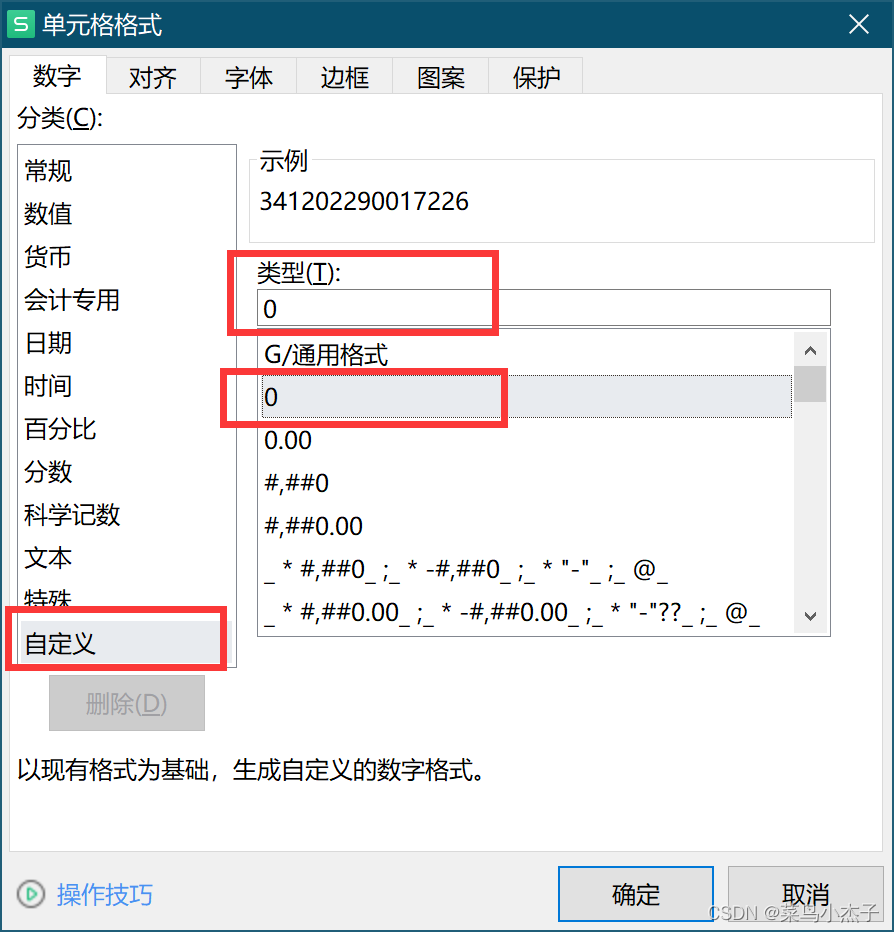
JAVA使用poi解析execl解决数值被转为科学计数法(如:手机号、身份证号、电话、等)解决方法
1、原由 大家都知道数字在EXCEL表格中存储时有两种表现形式。1.数字作为数值存储。当数字作为数值存储时,单元格中的数字可以参与数学运算。2.数字作为文本存储。当数字作为文本存储时,单元格中的数值不能够参与数学运算。 数字作为文本存储时,如果没有更…...
的使用)
hive中substring_index()的使用
substring_index(str,delim,count)str:要处理的字符串delim:分隔符count:计数例子:strwww.wikibt.comsubstring_index(str,.,1)结果是:wwwsubstring_index(str,.,2)结果是:www.wikibt如果count是正数,那么就是从左往右数ÿ…...

LocalDateTime设置时间的年、月、日、时、分、秒、纳秒
如何把String/Date转成LocalDateTime参考String、Date与LocalDate、LocalTime、LocalDateTime之间互转 String、Date、LocalDateTime、Calendar与时间戳之间互相转化参考String、Date、LocalDateTime、Calendar与时间戳之间互相转化 方法介绍 withYear(int year) 指定日期的…...
C语言rand和srand用法详解
在实际编程中,我们经常需要生成随机数,例如,贪吃蛇游戏中在随机的位置出现食物,扑克牌游戏中随机发牌。在C语言中,我们一般使用 <stdlib.h> 头文件中的 rand() 函数来生成随机数,它的用法为ÿ…...

安装作业
1、安装方法 mysql安装常见的方法有四种 序号安装方式说明1yum\rpm简单、快速,不能定制参数2二进制解压,简单配置就可使用 免安装 mysql-a.b.c-linux2.x-x86_64.tar.gz3源码编译可以定制参数,安装时间长 mysql-a.b.c.tar.gz4源码制成rpm包把…...

电压放大器在非共线混频方法检测混凝土中的应用
实验名称:电压放大器在非共线混频方法检测混凝土中的应用研究方向:无损检测测试目的:无损检测是在不损伤或不干扰待测物体的结构材料的情况下,对其内部损伤进行探测的方法。传统无损检测法在仪器携带,操作程序…...
二十四、Gtk4-GtkExpression
GtkExpression是一种基本类型。它不是GObject的后代。GtkExpression提供了一种描述对值的引用的方法。GtkExpression需要求值才能获得值。 它类似于算术计算。 1 2 3 12是一个表达式。给出了计算的方法。3是来自表达式的值。求值是计算表达式并得到值。 GtkExpression是一种…...

Oracle Dataguard(主库为 Oracle rac 集群)配置教程(02)—— Oracle RAC 主库的相关操作
Oracle Dataguard(主库为 Oracle rac 集群)配置教程(02)—— Oracle RAC 主库的相关操作 / 本专栏详细讲解 Oracle Dataguard(Oracle 版本为11g,主库为双节点 Oracle rac 集群)的配置过程。主要…...

midjournery AI绘画使用指南
midjournery AI绘画使用指南 基于Discord的Midjournery配置: https://www.bilibili.com/video/BV16d4y1A7Zq/?spm_id_from333.337.search-card.all.click&vd_source9c3ca9555620bed64bdee27ae49d37cf 使用原则 使用midjournery绘画的原则是给出对脑海中某个…...

iptables防火墙SNAT和DNAT
iptables防火墙SNAT和DNAT一、SNAT原理和应用1、SNAT原理2、SNAT应用环境3、SNAT转换前提条件二、SNAT案列1、实验需求2、实验环境3、实验目的三、DNAT原理和应用1、DNAT原理2、DNAT 应用环境3、DNAT转换的前提条件四、DNAT案列总结一、SNAT原理和应用 1、SNAT原理 SNAT原理:…...
python | 第二章考试题和练习题
一、考试题 1、turtle八边形绘制 问题描述: 使用turtle库,绘制一个八边形。 参考代码: import turtle as t t.pensize(2) for i in range(8):t.fd(100)t.left(45) 2、turtle八角图形绘制 问题描述: 使用turtle库,…...

Mysql 存储引擎设计:xa协议相关接口功能及实现
需要对接的接口以及每个接口的实现 recovery 阶段 此阶段由 xa.cc 文件中的 xarecover_handlerton() 函数完成,它通过三个接口实现与存储引擎的沟通:recover(),commit_by_xid() ,rollback_by_xid()。其流程如下: 此…...
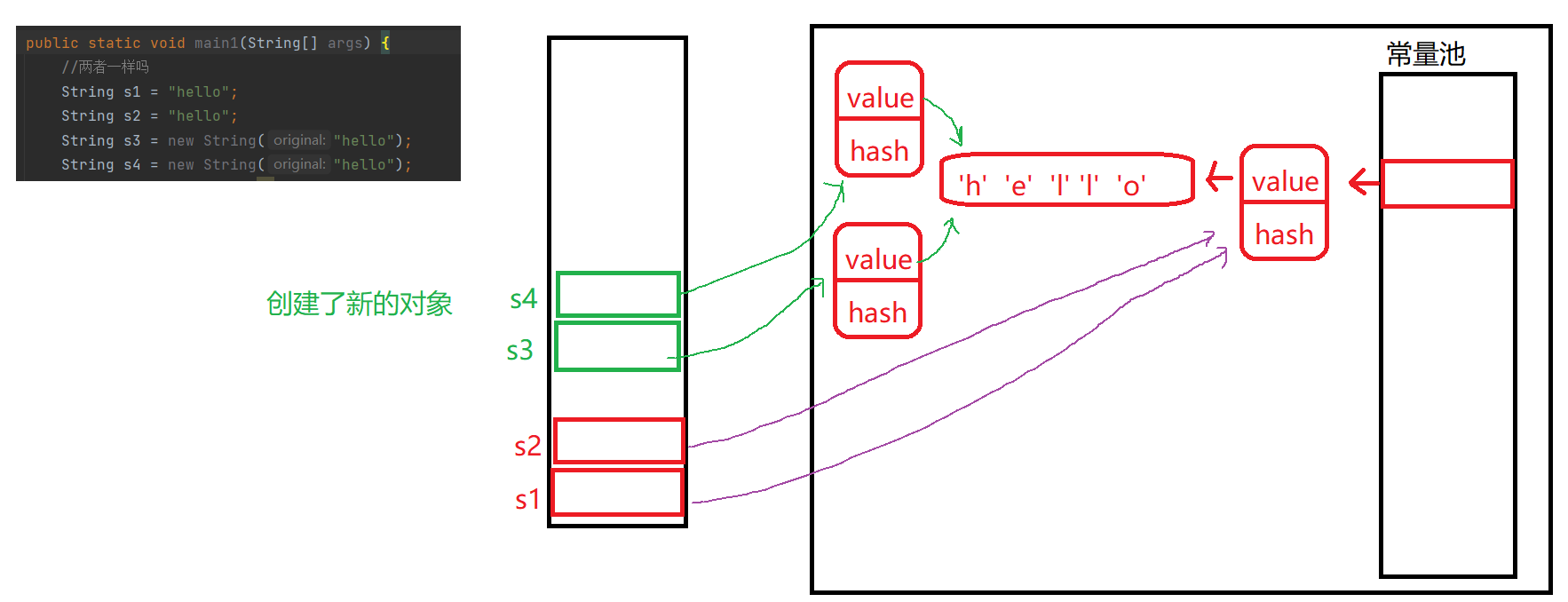
字符串常量池
1.创建对象的思考下面两种创建字符串的方式一样吗?public static void main(String[] args) {//两者一样吗String s1 "hello";String s2 "hello";String s3 new String("hello");String s4 new String("hello");System…...

让技术更有温度,腾讯Light 点亮公益之光
蓝天白云,远处是广东最长跨海大桥——南澳大桥,一艘小船在海面驶过,近处一头中华白海豚露出水面。在第三届腾讯Light技术公益创造营上,海南智渔可持续发展研究中心科学总监郑锐强为我们展现这样一幅人与自然和平相处的美好画面。随…...
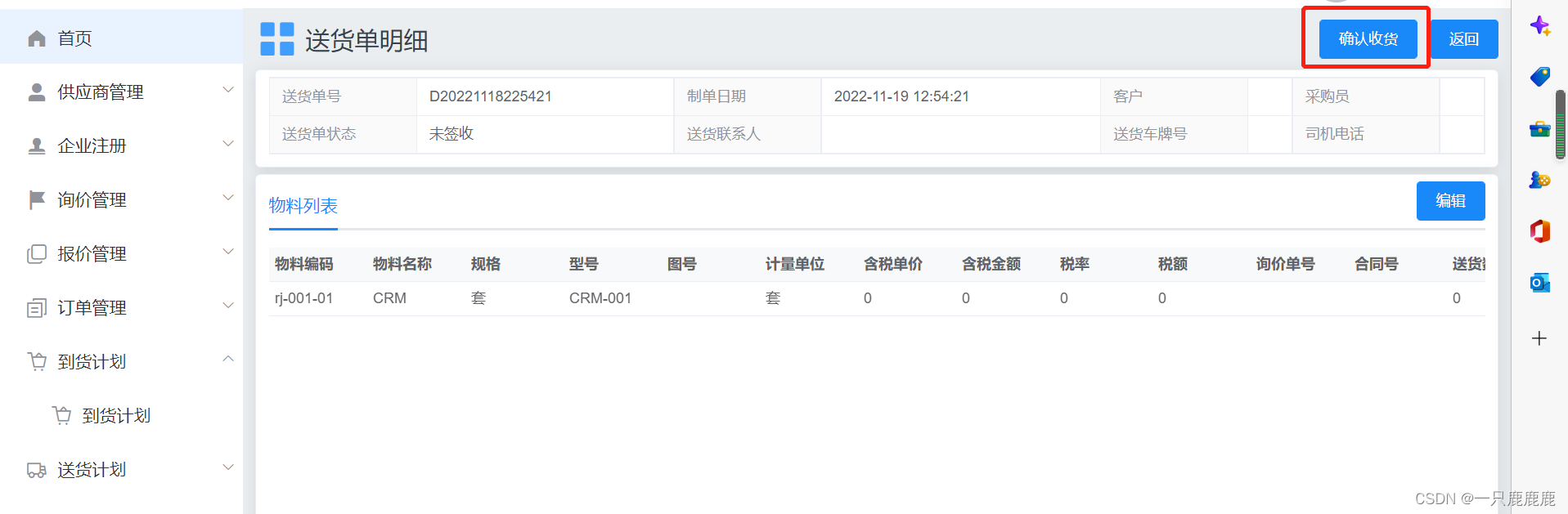
电子采购一体化解决方案
企事业数字化转型专家,提供各类应用解决方案。您身边的赋能小助手! 文章目录前言一、当下采购的痛点二、解决方案-供应商管理1.供应商管理三、解决方案-企业询价、供应商报价管理四、解决方案-采购订单五、送货、到货、订单管理总结前言 随着各类产业链…...
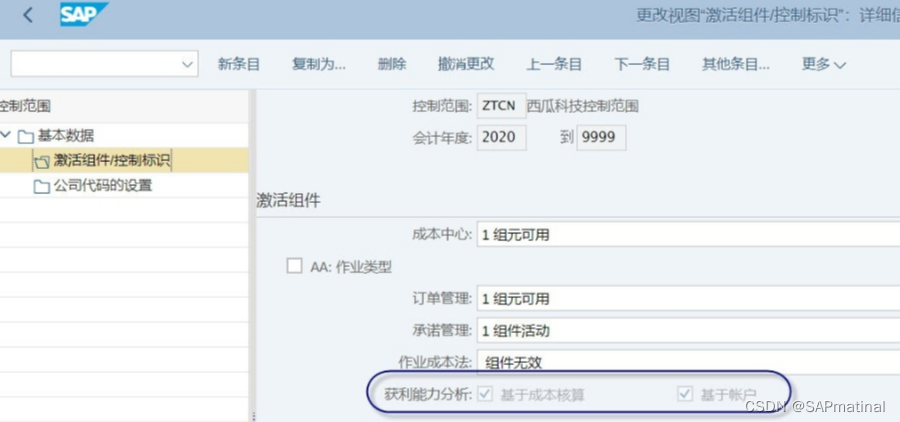
SAP COPA 获利能力分析深度解析
一、获利分析配置及相关值概述 二、配置:组织结构 2.1 定义经营范围-KEP8 2.2 维护经营关注点-KEA0 2.3 获利能力分析类型解析 2.4 控制范围分配给经营范围-KEKK 三、配置:数据结构-KEA0 3.1 特征字段 3.1.1 特征字段类别 3.1.2 维护特征字段-K…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...

【51单片机】4. 模块化编程与LCD1602Debug
1. 什么是模块化编程 传统编程会将所有函数放在main.c中,如果使用的模块多,一个文件内会有很多代码,不利于组织和管理 模块化编程则是将各个模块的代码放在不同的.c文件里,在.h文件里提供外部可调用函数声明,其他.c文…...

Centos 7 服务器部署多网站
一、准备工作 安装 Apache bash sudo yum install httpd -y sudo systemctl start httpd sudo systemctl enable httpd创建网站目录 假设部署 2 个网站,目录结构如下: bash sudo mkdir -p /var/www/site1/html sudo mkdir -p /var/www/site2/html添加测试…...

第21节 Node.js 多进程
Node.js本身是以单线程的模式运行的,但它使用的是事件驱动来处理并发,这样有助于我们在多核 cpu 的系统上创建多个子进程,从而提高性能。 每个子进程总是带有三个流对象:child.stdin, child.stdout和child.stderr。他们可能会共享…...

触发DMA传输错误中断问题排查
在STM32项目中,集成BLE模块后触发DMA传输错误中断(DMA2_Stream1_IRQHandler进入错误流程),但单独运行BLE模块时正常,表明问题可能源于原有线程与BLE模块的交互冲突。以下是逐步排查与解决方案: 一、问题根源…...
可视化图解算法48:有效括号序列
牛客网 面试笔试 TOP101 | LeetCode 20. 有效的括号 1. 题目 描述 给出一个仅包含字符(,),{,},[和],的字符串,判断给出的字符串是否是合法的括号序列 括号必须以正确的顺序关闭,"()"和"()[]{}"都是合法的括号序列&…...

【优选算法】模拟 问题算法
一:替换所有的问号 class Solution { public:string modifyString(string s) {int n s.size();for(int i 0; i < n; i){if(s[i] ?){for(char ch a; ch < z; ch){if((i0 && ch !s[i1]) || (in-1 && ch ! s[i-1]) || ( i>0 &&…...
