uniapp打包安卓后在安卓屏上实现开机自启动
实现开机自启动(使用插件)
打开插件地址安卓开机自启动 Fvv-AutoStart - DCloud 插件市场
使用方法
 选择你要开启自启动的项目
选择你要开启自启动的项目
在项目的manifest.json中app-plus下写入以下代码

注意需要替换 android_package_name 为自己的,不然无法进行安卓apk打包
"nativePlugins" : {"Fvv-AutoStart" : {"__plugin_info__" : {"name" : "安卓开机自启动 Fvv-AutoStart","description" : "uni-app 安卓开机自启动插件,不保证所有机型和系统都有效","platforms" : "Android","url" : "https://ext.dcloud.net.cn/plugin?id=1820","android_package_name" : "写自己的","ios_bundle_id" : "","isCloud" : true,"bought" : 1,"pid" : "1820","parameters" : {}}}
}然后在app权限配置中打开此选项
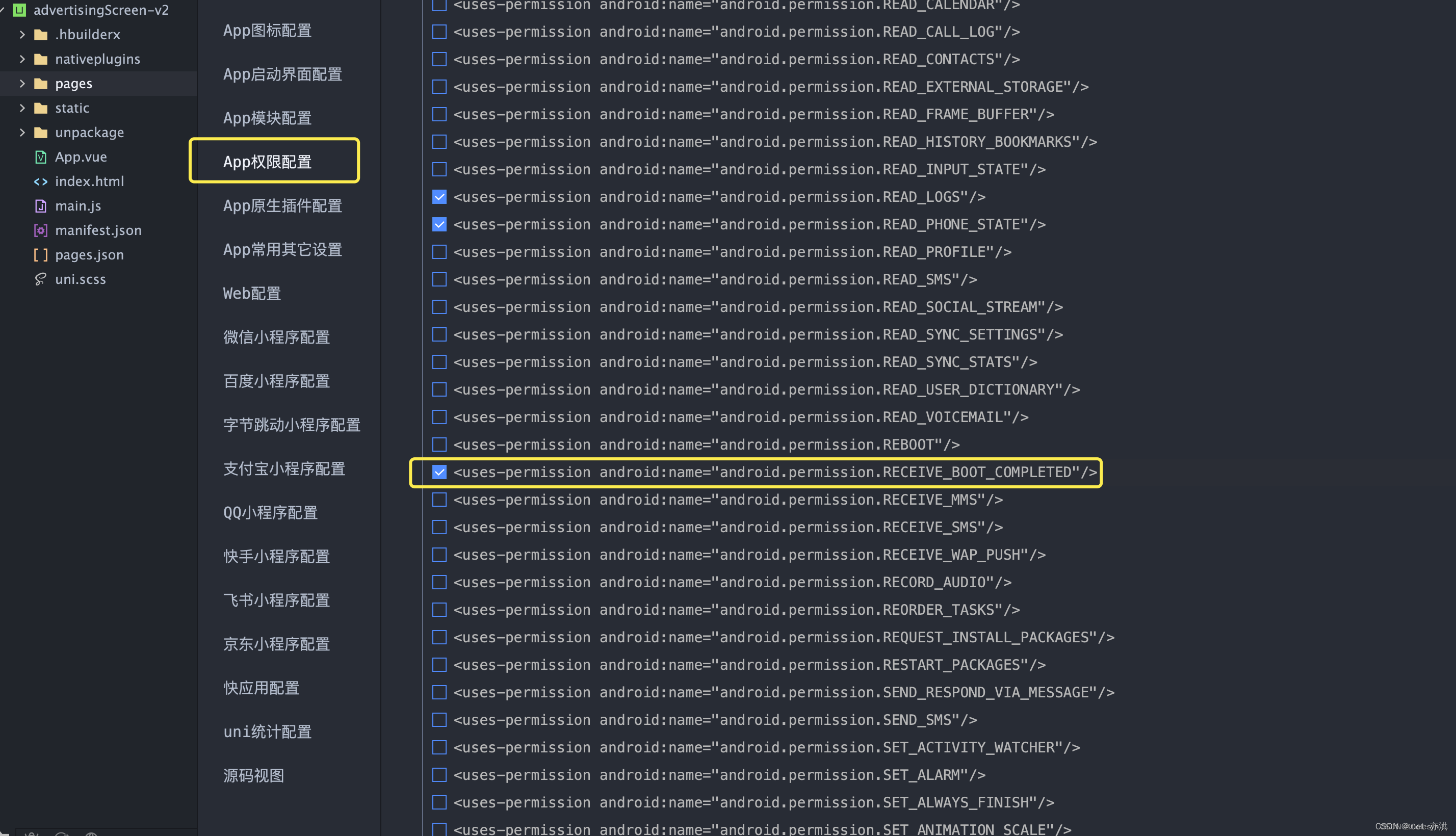
然后打包后安卓在安卓上即可实现开机自启动
实现无网状态下,读取缓存,有网时读实时数据,不影响数据的展示
onLoad() {this.loadData();
},
// methods 下
loadData() {uni.getNetworkType({success: (res) => {console.log(res)if (res.networkType === 'none') {// 无网络连接,从本地缓存中读取数据const data = uni.getStorageSync('listData')if (data) {this.listData = data}} else {// 有网络连接,通过网络请求获取数据uni.request({url: 'https://xxx.com/list',success: (res) => {this.listData = res.data// 将数据保存到本地缓存中uni.setStorageSync('listData', res.data)}})}}})
}
相关文章:

uniapp打包安卓后在安卓屏上实现开机自启动
实现开机自启动(使用插件) 打开插件地址安卓开机自启动 Fvv-AutoStart - DCloud 插件市场 使用方法 选择你要开启自启动的项目 在项目的manifest.json中app-plus下写入以下代码 注意需要替换 android_package_name 为自己的,不然无法进行安卓apk打包 "nativePlugins&q…...

浅谈KNX总线智能照明控制系统在北京南站房中的应用
安科瑞 华楠 摘要:本文简要介绍了i-bus EIB/KNX智能建筑控制系统的基本原理及在北京南站房中的成功应用。阐述了这一系统强大的系统功能、灵活的控制方式节能效果。 关键词:i-bus智能建筑控制;控制系统;节能 1、工程概况 北京新…...

深入了解Java的核心库
掌握Java的核心库是成为一名优秀的Java开发者的关键。Java提供了丰富的核心库和API,包括集合框架、输入输出、多线程、异常处理等等。熟悉并掌握这些库的使用,可以提高编程效率和代码质量。在本文中,我们将深入讨论Java的核心库,并…...
嵌入式:驱动开发 Day9
作业:通过platform总线驱动实现 a.应用程序通过阻塞的io模型来读取number变量的值 b.number是内核驱动中的一个变量 c.number的值随着按键按下而改变(按键中断) 例如number0 按下按键number1 ,再次按下按键number0 d.在按下按键的时候需要同时…...

【ComfyUI】安装 之 window版
文章目录 序言步骤下载comfyUI配置大模型和vae下载依赖组件启动 生成图片解决办法 序言 由于stable diffusion web ui无法做到对流程进行控制,只是点击个生成按钮后,一切都交给AI来处理。但是用于生产生活是需要精细化对各个流程都要进行控制的。 故也…...
iMazing 2 .17.9最新官方中文版免费下载安装激活
iMazing 2 .17.9最新版是一款帮助用户管理IOS手机的应用程序,iMazing2最新版能力远超iTunes提供的终极的iOS设备管理器。IMazing与你的iOS设备(iPhone、 iPad或iPod)相连,使用起来非常的方便。作为苹果指定的iOS设备同步工具。 mazing什么意思 iMazing…...
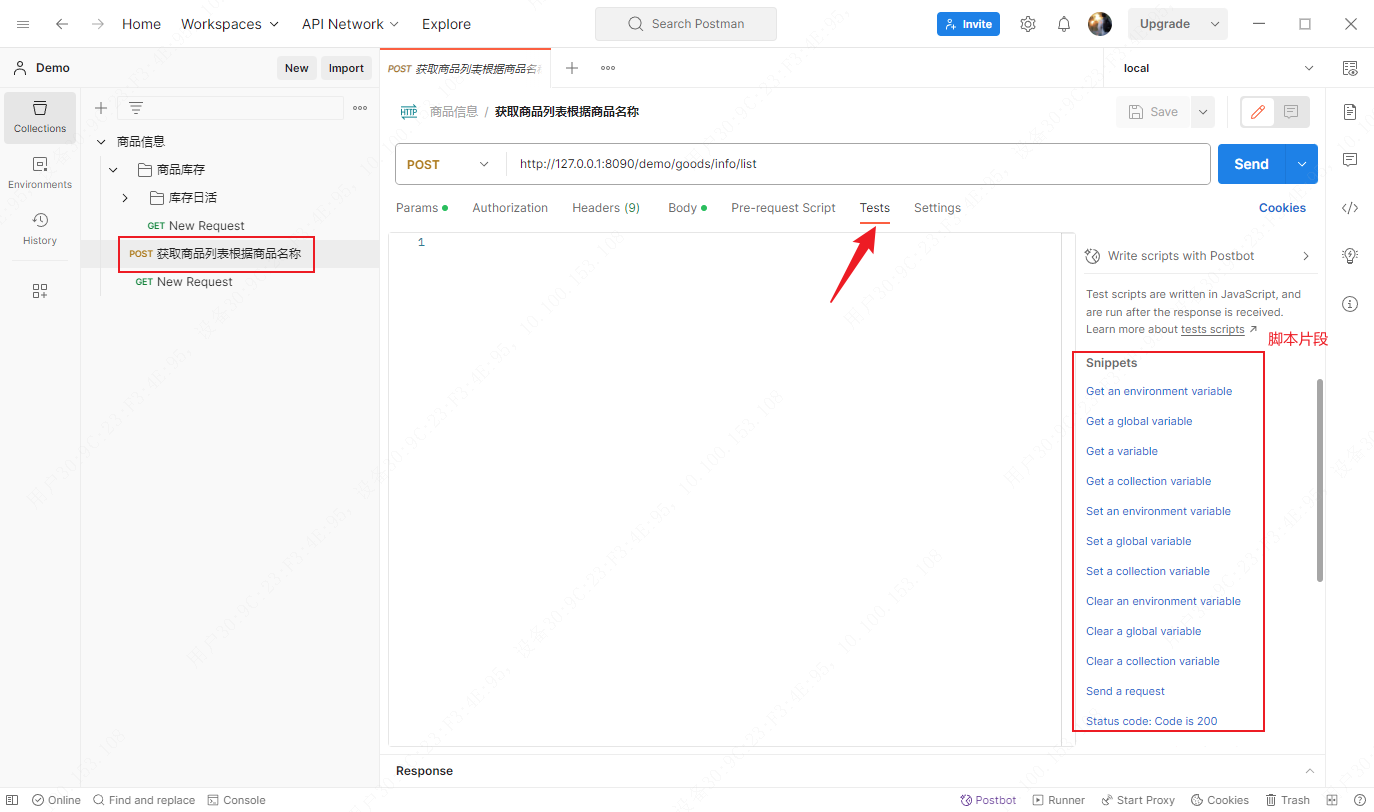
Postman应用——Pre-request Script和Test Script脚本介绍
文章目录 Pre-request Script所在位置CollectionFolderRequest Test Script所在位置CollectionFolderRequest Pre-request Script(前置脚本):可以使用在Collection、Folder和Request中,并在Request请求之前执行,可用于…...
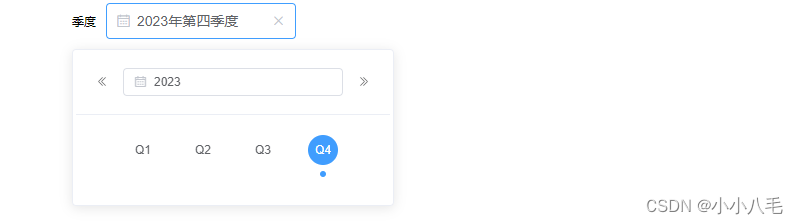
vue2中年份季度选择器(需要安装element)
调用 <!--父组件调用--><QuarterCom v-model"quart" clearable default-current/> 组件代码 <template><div><span style"margin-right: 10px">{{ label }}</span><markstyle"position:fixed;top:0;bottom:0…...
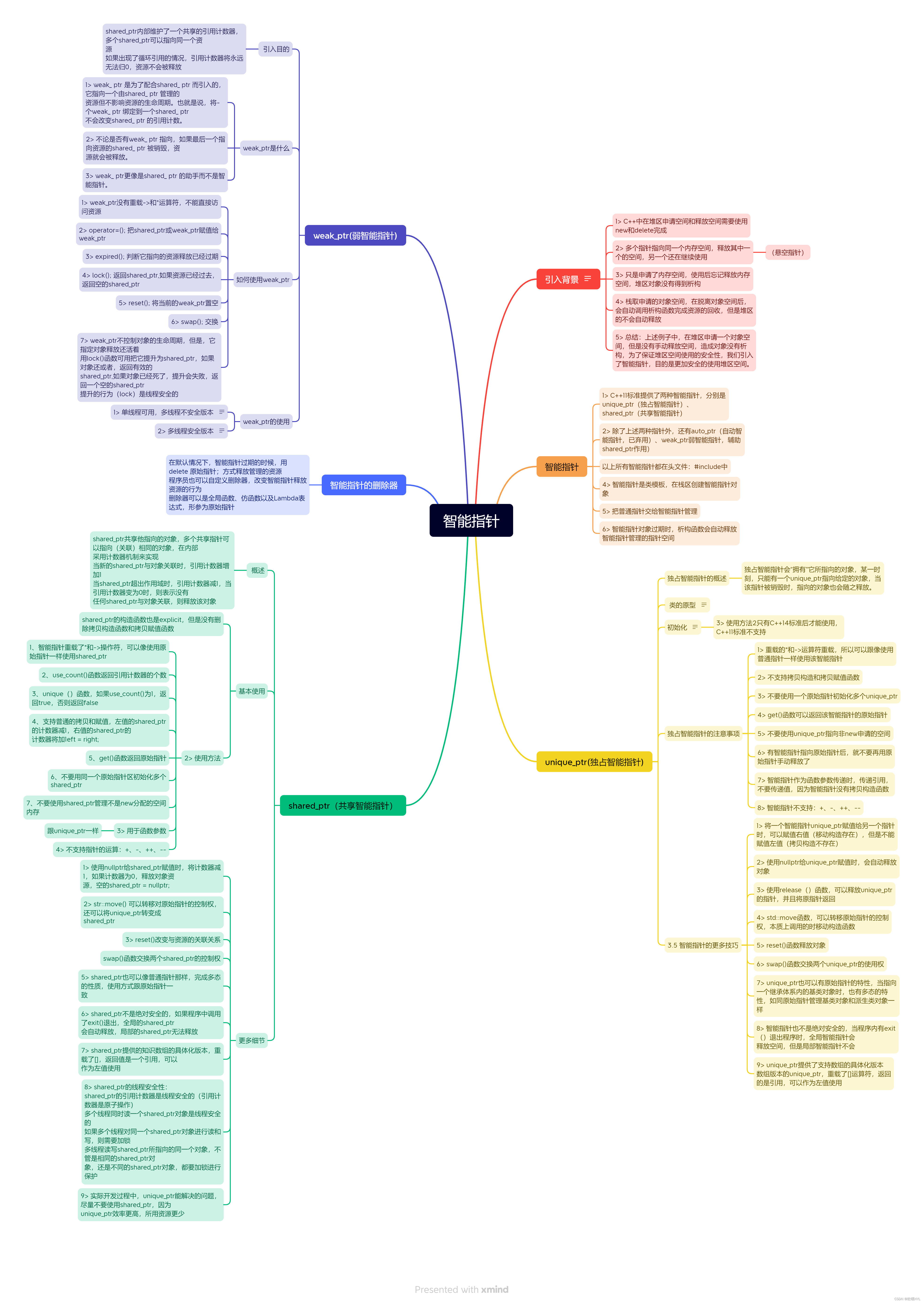
QT day5
数据库完成登入注册 mainwindow.h #ifndef MAINWINDOW_H #define MAINWINDOW_H #include <QMainWindow> #include<QDebug> #include<QPushButton> #include<QLineEdit> #include<QLabel> #include <QMainWindow> #include<QMessageBo…...

设计模式Java实战
文章目录 一、前置1.1 目的1.2 面向对象1.3 接口和抽象类 二、七大设计原则2.1 单一职责2.2 接口隔离原则2.3 依赖倒转原则2.4 里氏替换原则2.5 开闭原则2.6 不要重复原则2.7 迪米特最少知道法则 三、23种设计模式3.1创建型:创建对象3.1.1 单例模式定义最佳实践场景…...

外国固定资产管理系统功能有哪些
很多公司都在寻找提高自己资产管理效益的方法。为了满足这一要求,国外的固定资产管理系统已经发展成多种形式。以下是国外一些常见的固定资产管理系统的特点:自动化和智能化:许多现代固定资产管理系统采用自动化和数字化技术,以简化流程,减少…...
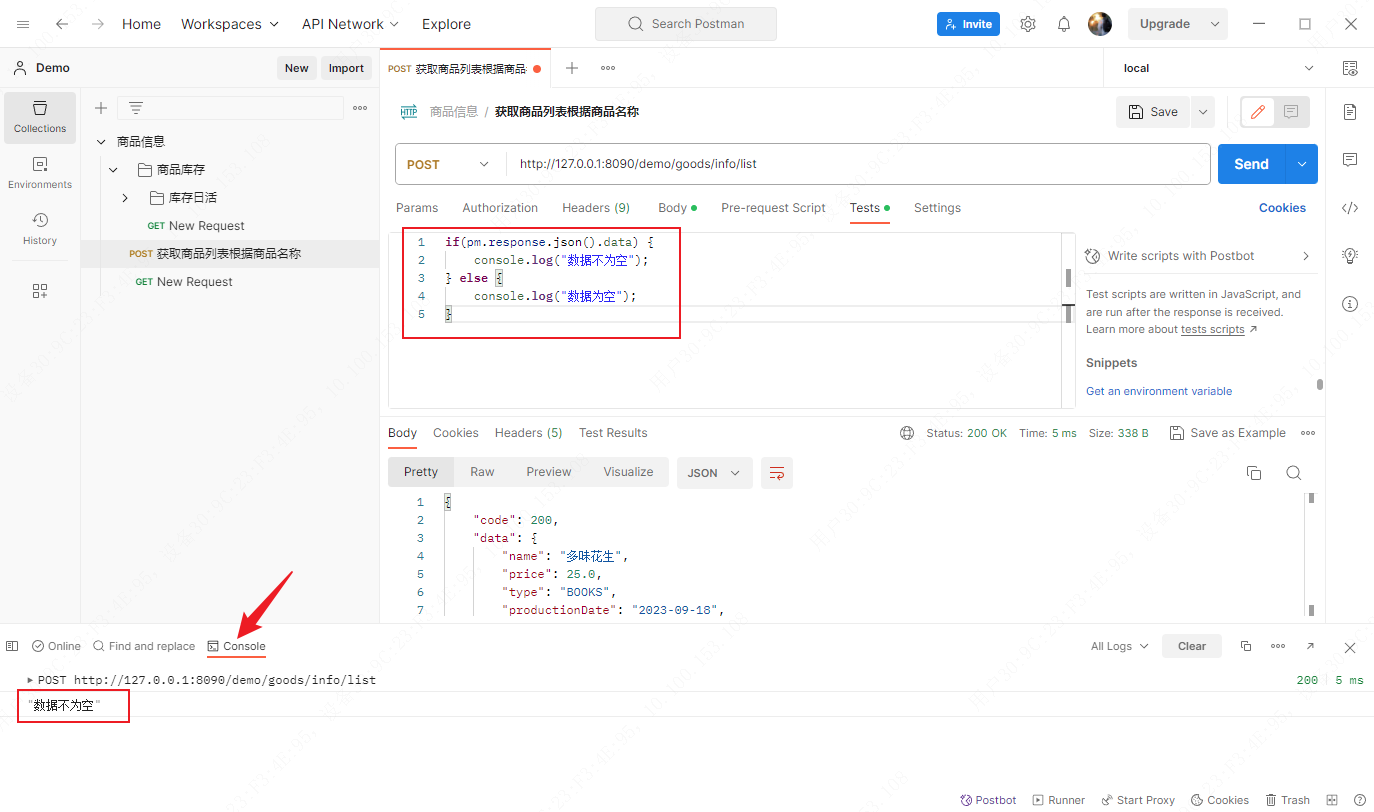
Postman应用——控制台调试
当你在测试脚本中遇到错误或意外行为时,Postman控制台可以帮助你识别,通过将console.log调试语句与你的测试断言相结合,你可以检查http请求和响应的内容,以及变量之类的。 通常可以使用控制台日志来标记代码执行,有时…...

如何制作思维导图?
思维导图是一种非常有用的工具,可以被广泛应用于不同领域的人群。以下是一些常见的使用人群:学生、教育工作人员、各领域的专业人员,法律、商业、医学等等,创作者、艺术家、个人自我成长管理。 由此可见,思维导图可以做…...

【力扣每日一题】2023.9.21 收集树中金币
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 题目给我们一棵树,不过这棵树不是普通的树,而是无向无根树。给我们一个二维数组表示节点之间的连接关系ÿ…...
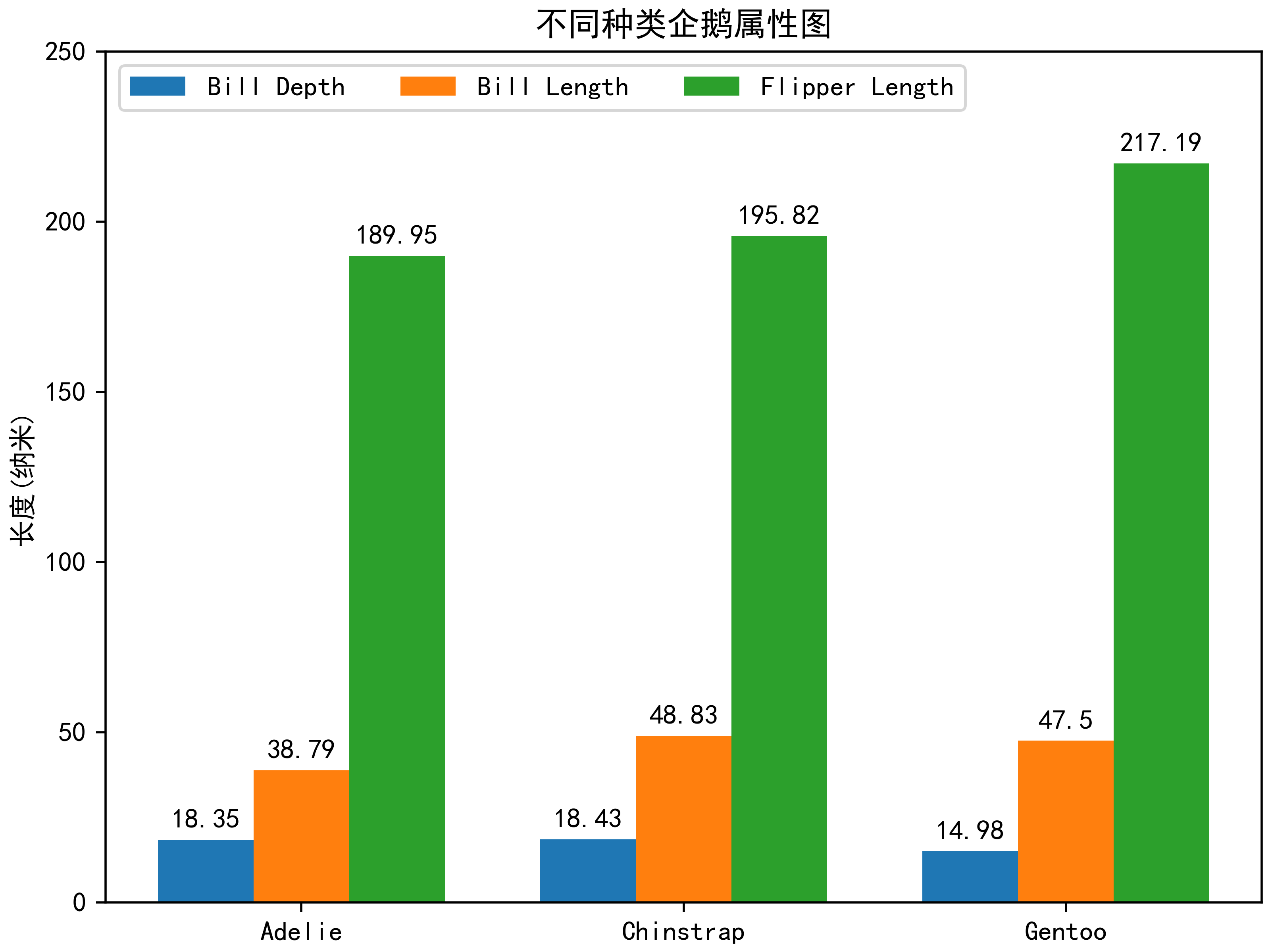
Python与数据分析--每天绘制Matplotlib库实例图片3张-第1天
目录 1.实例1--Bar color demo 2.实例2--Bar Label Demo 3.实例3--Grouped bar chart with labels 1.实例1--Bar color demo import matplotlib.pyplot as plt # 支持中文 plt.rcParams[font.sans-serif] [SimHei] # 用来正常显示中文标签 plt.rcParams[axes.unicode_minus…...
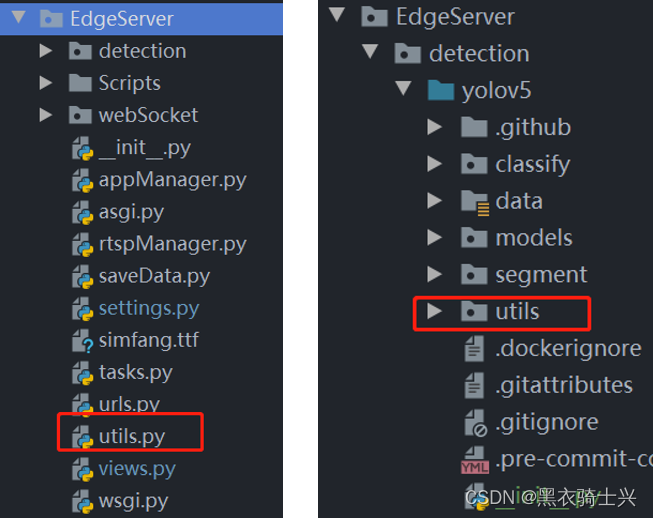
pycharm 中package, directory, sources root, resources root的区别
【遇到的问题】 导入yolov5中有utils文件,自己的代码中也有utils文件,使得yolov5中的这部分引用出错了。 【解决方案】 单独建立detection文件夹,把检测相关的都放在这里,yolov5是github上拉取的源码,发现yolov5中fr…...
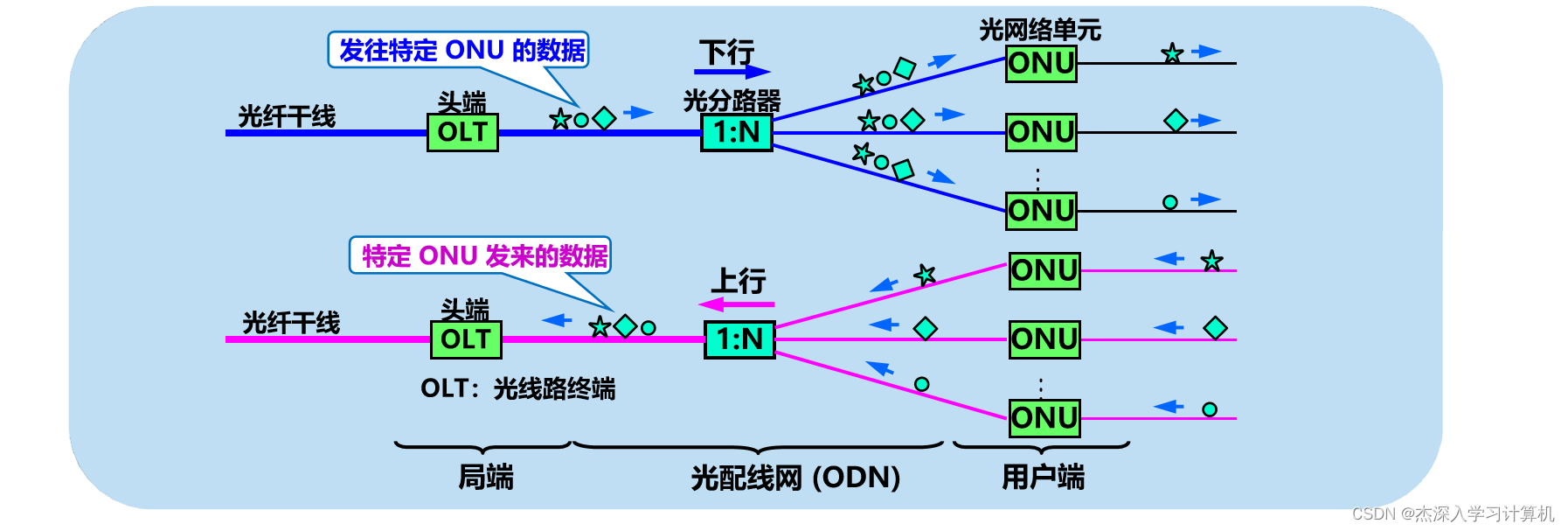
【谢希尔 计算机网络】第2章 物理层
目录 通信基础 基本概念 两个公式lim 奈氏准则 香农定理 奈氏准则 VS 香农定理 编码与调制 编辑 物理层下面的传输媒体 导引型传输媒体 1. 双绞线 2. 同轴电缆 3. 光缆 非导引型传输媒体 无线电微波通信 卫星通信 无线局域网使用的 ISM 频段 信道复用技术 …...

Eclipse工具使用技巧
1、常用快捷键 ctrlshifto 快速导包 CtrlSpace 内容助理 说明:内容助理。提供对方法,变量,参数,javadoc等得提示,应运在多种场合,总之需要提示的时候可先按此快捷键。注:避免输入法的切换设置与此设置冲突 CtrlShiftSpace 变量提示 Ctrl/ 添加/消除//注释 CtrlShift/ 添加…...

python LeetCode 刷题记录 94
题目 给定一个二叉树的根节点 root ,返回 它的 中序 遍历 代码 递归 # Definition for a binary tree node. # class TreeNode: # def __init__(self, val0, leftNone, rightNone): # self.val val # self.left left # self.righ…...

滴滴可观测平台 Metrics 指标实时计算如何实现了又准又省?
在滴滴,可观测平台的 Metrics 数据有一些实时计算的需求,承载这些实时计算需求的是一套又一套的 Flink 任务。之所以会有多套 Flink 任务,是因为每个服务按照其业务观测需要不同的指标计算,也就对应了不同数据处理拓扑。我们尽力抽…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...
