越狱(快速幂C++)
题目
监狱有连续编号为 11 到 n 的 n 个房间,每个房间关押一个犯人。
有 m 种宗教,每个犯人可能信仰其中一种。
不存在没有信仰的犯人。
如果相邻房间的犯人信仰的宗教相同,就可能发生越狱。
求有多少种状态可能发生越狱。
输入格式
共一行,包含两个整数 m和 n。
输出格式
可能越狱的状态数,对 100003100003 取余。
数据范围
1≤m≤108
1≤n≤1012
输入样例:
2 3
输出样例:
6
样例解释
所有可能的 66 种状态为:(000)(001)(011)(100)(110)(111)(000)(001)(011)(100)(110)(111)。
代码
#include<iostream>using namespace std;typedef long long LL;const int mod = 100003;int qmi(int a, LL b)
{LL res = 1;while(b){if(b & 1) res = res * a % mod;b >>= 1;a = (LL) a * a % mod;}return res;
}int main()
{int m;LL n;cin >> m >> n;// +mod防止出现负数情况 cout << (qmi(m, n) - (LL)m * qmi(m - 1, n - 1) % mod + mod) % mod<< endl;// 总分配方案数 - 不会发生越狱的方案数//不会发生越狱时,第一个人随便分配,第二个人信仰为m - 1, 第三个人信仰也为 m - 1 return 0;
}相关文章:
)
越狱(快速幂C++)
题目 监狱有连续编号为 11 到 n 的 n 个房间,每个房间关押一个犯人。 有 m 种宗教,每个犯人可能信仰其中一种。 不存在没有信仰的犯人。 如果相邻房间的犯人信仰的宗教相同,就可能发生越狱。 求有多少种状态可能发生越狱。 输入格式 共…...

电脑入门:怎么进入路由器设置
怎么进入路由器设置 在浏览器地址栏上输入路由器的出厂默认IP地址(192.168.0.1)后按回车。在登录窗口中输入说明书上的密码,点击“Log in”按钮进入宽带路由器管理设置界面。 管理设置界面分为左右栏,左栏是主菜单,右边则是与之对应的设置内容。 请根据自己接…...

Vue3大屏项目实现数字跳动的效果
一、vue-count-to组件: 1、安装: npm install vue3-count-to --save 2、使用: <template><BaseCountTo:startVal"startVal":endVal"endVal":duration"duration":decimals"decimals":pr…...
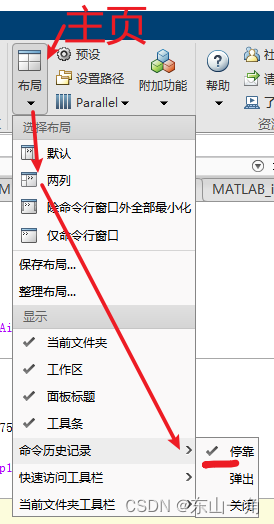
MATLAB打开历史命令窗口并保持
版本:matlab 2021a 方法:菜单栏 主页 - 布局 - 命令历史记录 - 停靠...
等差数列和等比数列 常用公式
等差数列 定义 通项公式 , 公差 , 前n项和公式 中项公式 下标:mnpq,则 等比数列 定义 通项公式 , 公比 , 前n项和公式 , 中项公式 下标:mnpq,则...
基于SpringBoot+Vue的MOBA类游戏攻略分享平台
1 简介 MOBA类游戏攻略分享平台,为用户随时随地查看游戏攻略信息提供了便捷的方法,更重要的是大大的简化了管理员管理MOBA类游戏攻略信息的方式方法,更提供了其他想要了解MOBA类游戏攻略信息及运作情况以及挑选方便快捷的可靠渠道。相比于传…...
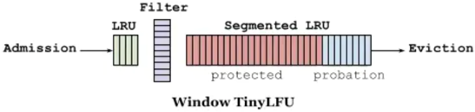
基于异常上线场景的实时拦截与问题分发策略
作者 | 彭阳 导读 性能中台负责MEG端研发数据的接入、传输、管理、应用等各个环节。为了应对移动应用领域中端技术的快速迭代和线上突增问题的挑战,中台提出了实时拦截与问题的分发机制,旨在在端上线的不同阶段及时发现并拦截异常上线,最大程…...

MySQL常见面试题(一)
😀前言 在数据库管理系统中,存储引擎起着核心的角色,它决定了数据管理和存储的方式。MySQL作为一个领先的开源关系型数据库管理系统,提供了多种存储引擎来满足不同的需求和优化不同的应用。除了选择合适的存储引擎,数据…...

webpack:详解entry和output一些重要API的使用
文章目录 contextentry单个入口多个入口entry相关API例一例二例三 outputoutput.assetModuleFilenameoutput.chunkFilenameoutput.clean【5.20.0版本支持】output.filename【重要】output.globalObjectoutput.library【重要】output.library.nameoutput.library.type【重要】ou…...

Spring后处理器-BeanPostProcessor
Spring后处理器-BeanPostProcessor Bean被实例化后,到最终缓存到名为singletonObjects单例池之前,中间会经过bean的初始化过程((该后处理器的执行时机)),例如:属性的填充、初始化方…...

每日一题~修剪二叉树
原题链接:669. 修剪二叉搜索树 - 力扣(LeetCode) 题目描述: 思路分析: 由题可知,我们要将原来的二叉搜索树调整为值在 low~high 之间的新二叉搜索树,接下来我们分析一下针对不同的节点的处理方…...
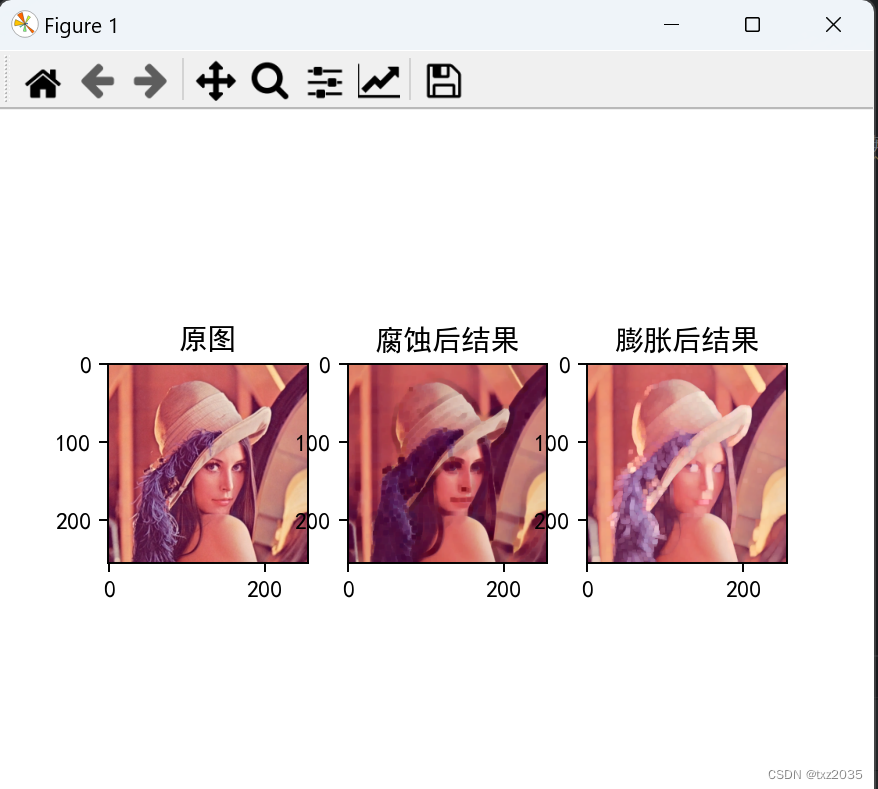
图像形态学操作(连通性、腐蚀、膨胀)
相关概念 形态学操作-腐蚀 参数: img: 要处理的图像kernal :核结构iteration :腐蚀的次数,默认是1 形态学操作-膨胀 参数: img : 要处理的图像kernal : 核结构iteration : 膨胀的次数,默认为1 import cv2 as cv im…...

中国这么多 Java 开发者,应该诞生出生态级应用开发框架
1、必须要有,不然就永远不会有 应用开发框架,虽然没有芯片、操作系统、数据库、编程语言这些重要。但是最终呈现在用户面前的,总是有软件部分。而软件系统开发,一般都需要应用开发框架,它是软件系统的基础性部件之一。…...

仿猫扑盒子引流神器试看神马视频-红包打卡签到领金
特点1:站内发红包,抢红包 特点2:会员可上传视频 特点3:设置每天免费试看次数…..具体看演示站点,为准 支付在后台上传收款二维码即可,支持微信和支付宝。前台提交订单后台管理员审核 环境:宝…...
WhatsApp自动营销软件是真实的吗?对做外贸有帮助吗?
出海营销少不了的就是依靠海外平台,WhatsApp作为许多海外国家和地区最受欢迎的聊天应用程序,活跃用户占到了全球人口的四分之一,有些地区比如欧洲、美洲,用户渗透率超过了80%,对海外营销的企业来说是不可缺少的销售工具…...

抖音短视频矩阵系统搭建
企业在进行短视频矩阵运营时,搭建一个矩阵号是非常必要的。矩阵号可以绑定多个不同平台的账号,批量制作和定时发布短视频,提高企业的曝光量和粉丝互动。但是,如何搭建一个有效的短视频矩阵号呢?以下是几个关键步骤。 一…...

Chinese-LLaMA-AIpaca
文章目录 关于 Chinese-LLaMA-Alpaca一、LLaMA模型 --> HF格式二、合并LoRA权重,生成全量模型权重方式1:单LoRA权重合并方式2:多LoRA权重合并(适用于Chinese-Alpaca-Plus )三、使用 Transformers 进行推理四、使用 webui 搭建界面1、克隆text-generation-webui并安装必…...

IP归属地应用的几个主要特点
作为一款优秀的IP地址定位工具,主题IP归属地的应用无疑是最好的选择之一。该应用可以将您需要查询的IP地址快速定位到所在的具体物理位置,并提供详细的地址和地图信息。接下来,让我们一起来看一看IP归属地应用的几个主要特点: 1. …...
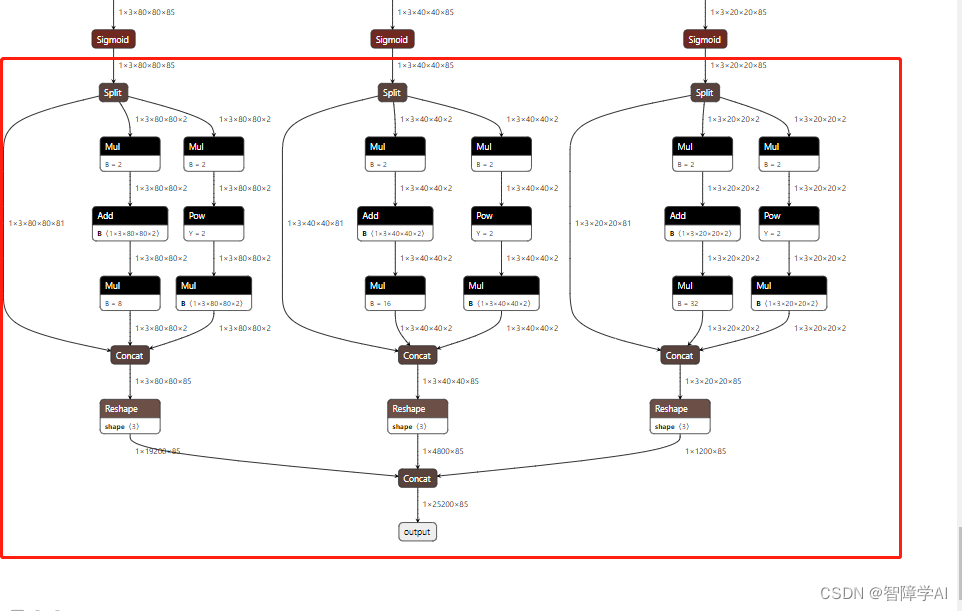
通过解读yolov5_gpu_optimization学习如何使用onnx_surgon
onnx实战一: 解析yolov5 gpu的onnx优化案例: 这是一个英伟达的仓库, 这个仓库的做法就是通过用gs对onnx进行修改减少算子然后最后使用TensorRT插件实现算子, 左边是优化过的, 右边是原版的。 通过这个案例理解原版的onnx的导出流程然后我们看英伟达是怎么拿gs来优化…...

图像复原与重建,解决噪声的几种空间域复原方法(数字图像处理概念 P4)
文章目录 图像复原模型噪声模型只存在噪声的空间域复原 图像复原模型 噪声模型 只存在噪声的空间域复原...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
