数据结构与算法(四):树结构
前面讲到的顺序表、栈和队列都是一对一的线性结构,这节讲一对多的线性结构——树。「一对多」就是指一个元素只能有一个前驱,但可以有多个后继。
一、基本概念
树(tree)是n(n>=0)个结点的有穷集。n=0时称为空树。在任意一个非空树中:(1)每个元素称为结点(node);(2)仅有一个特定的结点被称为根结点或树根(root)。(3)当n>1时,其余结点可分为m(m≥0)个互不相交的集合T1,T2,……Tm,其中每一个集合Ti(1<=i<=m)本身也是一棵树,被称作根的子树(subtree)。
注意:
- n>0时,根节点是唯一的。
- m>0时,子树的个数没有限制,但它们一定是互不相交的。
结点拥有的子树数被称为结点的度(Degree)。度为0的结点称为叶节点(Leaf)或终端结点,度不为0的结点称为分支结点。除根结点外,分支结点也被称为内部结点。结点的子树的根称为该结点的孩子(Child),该结点称为孩子的双亲或父结点。同一个双亲的孩子之间互称为兄弟。树的度是树中各个结点度的最大值。
结点的层次(Level)从根开始定义起,根为第一层,根的孩子为第二层。双亲在同一层的结点互为堂兄弟。树中结点的最大层次称为树的深度(Depth)或高度。如果将树中结点的各个子树看成从左到右是有次序的,不能互换的,则称该树为有序树,否则称为无序树。森林是m(m>=0)棵互不相交的树的集合。
树的定义:
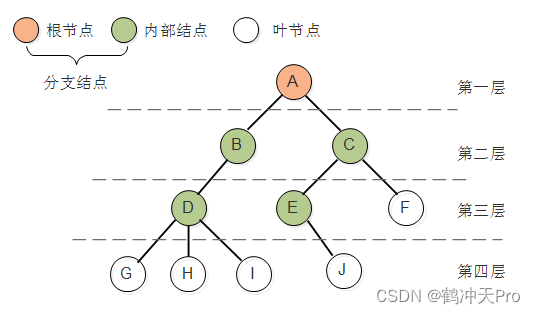
二、树的存储结构
由于树中每个结点的孩子可以有多个,所以简单的顺序存储结构无法满足树的实现要求。下面介绍三种常用的表示树的方法:双亲表示法、孩子表示法和孩子兄弟表示法。
1、双亲表示法
由于树中每个结点都仅有一个双亲结点(根节点没有),我们可以使用指向双亲结点的指针来表示树中结点的关系。这种表示法有点类似于前面介绍的静态链表的表示方法。具体做法是以一组连续空间存储树的结点,同时在每个结点中,设一个「游标」指向其双亲结点在数组中的位置。代码如下:
public class PTree<E> {private static final int DEFAULT_CAPACITY = 100;private int size;private Node[] nodes;private class Node() {E data;int parent;Node(E data, int parent) {this.data = data;this.parent = parent;}}public PTree() {nodes = new PTree.Node[DEFAULT_CAPACITY];}
}
由于根结点没有双亲结点,我们约定根节点的parent域值为-1。树的双亲表示法如下所示:
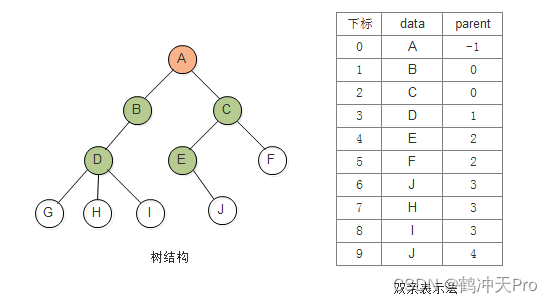
这样的存储结构,我们可以根据结点的parent域在O(1)的时间找到其双亲结点,但是只能通过遍历整棵树才能找到它的孩子结点。一种解决办法是在结点结构中增加其孩子结点的域,但若结点的孩子结点很多,结点结构将会变的很复杂。
2、孩子表示法
由于树中每个结点可能有多个孩子,可以考虑用多重链表,即每个结点有多个指针域,每个指针指向一个孩子结点,我们把这种方法叫多重链表表示法。它有两种设计方案:
方案一:指针域的个数等于树的度。其结点结构可以表示为:
class Node() {E data;Node child1;Node child2;...Node childn;
}
对于上一节中的树,树的度为3,其实现为:
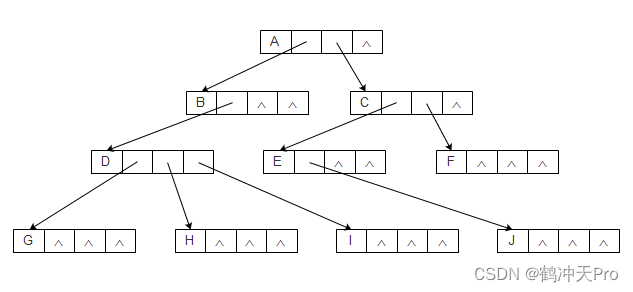
显然,当树中各结点的度相差很大时,这种方法对空间有很大的浪费。
方案二,每个结点指针域的个数等于该结点的度,取一个位置来存储结点指针的个数。其结点结构可以表示为:
class Node() {E data;int degree;Node[] nodes;Node(int degree) {this.degree = degree;nodes = new Node[degree];}
}
对于上一节中的树,这种方法的实现为:
这种方法克服了浪费空间的缺点,但由于各结点结构不同,在运算上会带来时间上的损耗。
为了减少空指针的浪费,同时又使结点相同。我们可以将顺序存储结构和链式存储结构相结合。具体做法是:把每个结点的孩子结点以单链表的形式链接起来,若是叶子结点则此单链表为空。然后将所有链表存放进一个一维数组中。这种表示方法被称为孩子表示法。其结构为:
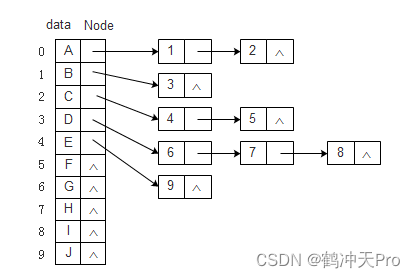
代码表示:
public class CTree<E> {private static final int DEFAULT_CAPACITY = 100;private int size;private Node[] nodes;private class Node() {E data;ChildNode firstChild;}//链表结点private class ChildNode() {int cur; //存放结点在nodes数组中的下标ChildNode next;}public CTree() {nodes = new CTree.Node[DEFAULT_CAPACITY];}
}
这种结构对于查找某个结点的孩子结点比较容易,但若想要查找它的双亲或兄弟,则需要遍历整棵树,比较麻烦。可以将双亲表示法和孩子表示法相结合,这种方法被称为双亲孩子表示法。其结构如下:
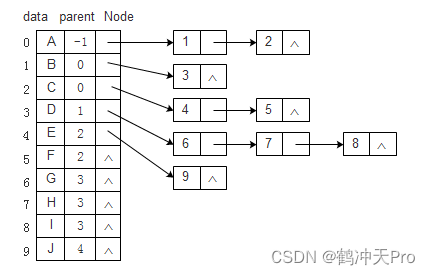
其代码和孩子表示法的基本相同,只需在Node结点中增加parent域即可。
3、孩子兄弟表示法
任意一棵树,它的结点的第一个孩子如果存在则是唯一的,它的右兄弟如果存在也是唯一的。因此,我们可以使用两个分别指向该结点的第一个孩子和右兄弟的指针来表示一颗树。其结点结构为:
class Node() {E data;Node firstChild;Node rightSib;
}
其结构如下:
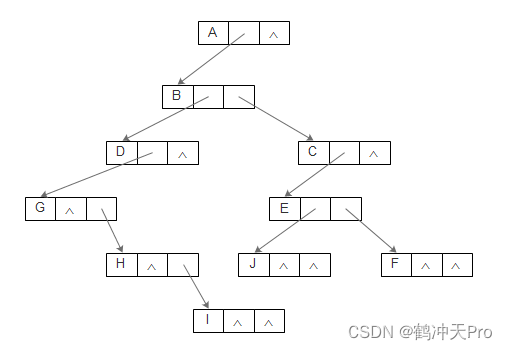
这个方法,可以方便的查找到某个结点的孩子,只需先通过firstChild找到它的第一个孩子,然后通过rightSib找到它的第二个孩子,接着一直下去,直到找到想要的孩子。若要查找某个结点的双亲和左兄弟,使用这个方法则比较麻烦。
这个方法最大的好处是将一颗复杂的树变成了一颗二叉树。这样就可以使用二叉树的一些特性和算法了。
三、二叉树
1、基本概念
二叉树(Binary Tree)是每个节点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。
二叉树的特点:
二叉树不存在度大于2的结点。
二叉树的子树有左右之分,次序不能颠倒。
如下图中,树1和树2是同一棵树,但它们是不同的二叉树。
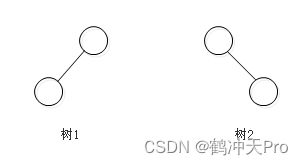
1)、斜树
所有的结点都只有左子树的二叉树叫左斜树。所有的结点都只有右子树的二叉树叫右斜树。这两者统称为斜树。
斜树每一层只有一个结点,结点的个数与二叉树的深度相同。其实斜树就是线性表结构。
2)、满二叉树
在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树。
满二叉树具有如下特点:
- 叶子只能出现在最下一层
- 非叶子结点的度一定是2
- 同样深度的二叉树中,满二叉树的结点个数最多,叶子数最多。
3)、完全二叉树
若设二叉树的高度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第h层有叶子结点,并且叶子结点都是从左到右依次排布,这就是完全二叉树。
完全二叉树的特点:
- 叶子结点只能出现在最下两层
- 最下层叶子在左部并且连续
- 同样结点数的二叉树,完全二叉树的深度最小
4)、平衡二叉树
平衡二叉树又被称为AVL树(区别于AVL算法),它是一棵二叉排序树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树
2、二叉树的性质
在二叉树的第i层上至多有2^i-1个结点(i>=1)。
深度为k的二叉树至多有2^k-1个结点(k>=1)。
对任何一棵二叉树T,如果其终端结点个数为n0,度为2的结点数为n2,则n0 = n2 + 1。
具有n个结点的完全二叉树的深度为「log2n」+ 1(「x」表示不大于x的最大整数)。
如果对一棵有n个结点的完全二叉树的结点按层序编号(从第一层到第「log2n」+ 1层,每层从左到右),对任一结点i(1≤i≤n)有:
若i=1,则结点i是二叉树的根,无双亲;如i>1,则其双亲是结点「i/2」。
如2i>n,则结点i无左孩子(结点i为叶子结点);否则其左孩子是结点2i。
若2i+1>n,则结点i无右孩子;否则其右孩子是结点2i+1。
3、二叉树的实现
二叉树是一种特殊的树,它的存储结构相对于前面谈到的一般树的存储结构要简单一些。
1)、顺序存储
二叉树的顺序存储结构就是用一维数组来存储二叉树中的结点。不使用数组的第一个位置。结点的存储位置反映了它们之间的逻辑关系:位置k的结点的双亲结点的位置为「k/2」,它的两个孩子结点的位置分别为2k和2k+1。

代码实现:
public class ArrayBinaryTree<E> {private static final int DEFAULT_DEPTH = 5;private int size = 0;private E[] datas;ArrayBinaryTree() {this(DEFAULT_DEPTH);}@SuppressWarnings("unchecked")ArrayBinaryTree(int depth) {datas = (E[]) new Object[(int)Math.pow(2, depth)];}public boolean isEmpty() { return size == 0; }public int size(){ return size; }public E getRoot() { return datas[1]; }// 返回指定节点的父节点 public E getParent(int index) { checkIndex(index); if (index == 1) { throw new RuntimeException("根节点不存在父节点!"); } return datas[index/2]; } //获取右子节点 public E getRight(int index){ checkIndex(index*2 + 1); return datas[index * 2 + 1]; } //获取左子节点 public E getLeft(int index){ checkIndex(index*2); return datas[index * 2]; } //返回指定数据的位置 public int indexOf(E data){ if(data==null){ throw new NullPointerException(); } else { for(int i=0;i<datas.length;i++) { if(data.equals(datas[i])) { return i; } } } return -1; }//顺序添加元素public void add(E element) {checkIndex(size + 1);datas[size + 1] = element;size++;}//在指定位置添加元素public void add(E element, int parent, boolean isLeft) {if(datas[parent] == null) { throw new RuntimeException("index["+parent+"] is not Exist!"); } if(element == null) { throw new NullPointerException(); } if(isLeft) {checkIndex(2*parent);if(datas[parent*2] != null) { throw new RuntimeException("index["+parent*2+"] is Exist!"); }datas[2*parent] = element;}else {checkIndex(2*parent + 1);if(datas[(parent+1)*2]!=null) { throw new RuntimeException("index["+ parent*2+1 +"] is Exist!"); } datas[2*parent + 1] = element;}size++;}//检查下标是否越界private void checkIndex(int index) { if(index <= 0 || index >= datas.length) { throw new IndexOutOfBoundsException(); } } public static void main(String[] args) {char[] data = {'A','B','C','D','E','F','G','H','I','J'};ArrayBinaryTree<Character> abt = new ArrayBinaryTree<>();for(int i=0; i<data.length; i++) {abt.add(data[i]);}System.out.print(abt.getParent(abt.indexOf('J')));}
}
一棵深度为k的右斜树,只有k个结点,但却需要分配2k-1个顺序存储空间。所以顺序存储结构一般只用于完全二叉树。
2)、链式存储
二叉树每个结点最多有两个孩子,所以为它设计一个数据域和两个指针域即可。我们称这样的链表为二叉链表。其结构如下图:
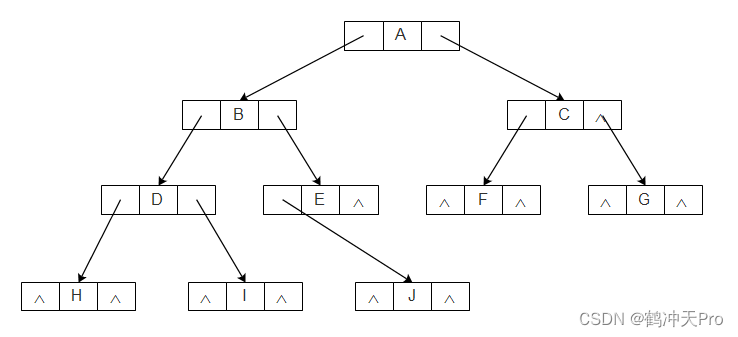
代码如下:
import java.util.*;
public class LinkedBinaryTree<E> { private List<Node> nodeList = null; private class Node { Node leftChild; Node rightChild; E data; Node(E data) { this.data = data; } } public Node getRoot() {return nodeList.get(0);}public void createBinTree(E[] array) { nodeList = new LinkedList<Node>(); for (int i = 0; i < array.length; i++) { nodeList.add(new Node(array[i])); } // 对前lasti-1个父节点按照父节点与孩子节点的数字关系建立二叉树 for (int i = 0; i < array.length / 2 - 1; i++) { nodeList.get(i).leftChild = nodeList.get(i * 2 + 1); nodeList.get(i).rightChild = nodeList.get(i * 2 + 2); } // 最后一个父节点:因为最后一个父节点可能没有右孩子,所以单独拿出来处理 int lastParent = array.length / 2 - 1; nodeList.get(lastParent).leftChild = nodeList .get(lastParent * 2 + 1); // 右孩子,如果数组的长度为奇数才建立右孩子 if (array.length % 2 == 1) { nodeList.get(lastParent).rightChild = nodeList.get(lastParent * 2 + 2); } } public static void main(String[] args) {Character[] data = {'A','B','C','D','E','F','G','H','I','J'};LinkedBinaryTree<Character> ldt = new LinkedBinaryTree<>();ldt.createBinTree(data);}
}
4、二叉树的遍历
二叉树的遍历(traversing binary tree)是指从根结点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次且仅被访问一次。
二叉树的遍历主要有四种:前序遍历、中序遍历、后序遍历和层序遍历。
1)、前序遍历
先访问根结点,然后遍历左子树,最后遍历右子树。
代码:
//顺序存储
public void preOrderTraverse(int index) { if (datas[index] == null) return; System.out.print(datas[index] + " "); preOrderTraverse(index*2); preOrderTraverse(index*2+1);
} //链式存储public void preOrderTraverse(Node node) { if (node == null) return; System.out.print(node.data + " "); preOrderTraverse(node.leftChild); preOrderTraverse(node.rightChild);
}
2)、中序遍历
先遍历左子树,然后遍历根结点,最后遍历右子树。
//链式存储public void inOrderTraverse(Node node) { if (node == null) return; inOrderTraverse(node.leftChild);System.out.print(node.data + " "); inOrderTraverse(node.rightChild);
}
3)、后序遍历
先遍历左子树,然后遍历右子树,最后遍历根结点。
//链式存储public void postOrderTraverse(Node node) { if (node == null) return; postOrderTraverse(node.leftChild);postOrderTraverse(node.rightChild); System.out.print(node.data + " ");
}
4)、层序遍历
从上到下逐层遍历,在同一层中,按从左到右的顺序遍历。如上一节中的二叉树层序遍历的结果为ABCDEFGHIJ。
注意:
- 已知前序遍历和中序遍历,可以唯一确定一棵二叉树。
- 已知后序遍历和中序遍历,可以唯一确定一棵二叉树。
- 已知前序遍历和后序遍历,不能确定一棵二叉树。
如前序遍历是ABC,后序遍历是CBA的二叉树有:
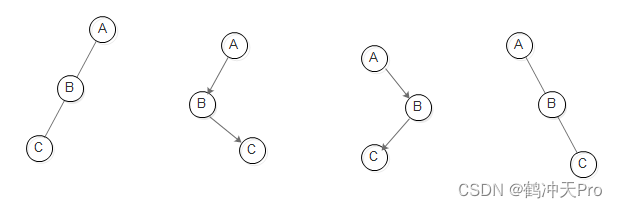
四、线索二叉树
对于n个结点的二叉树,在二叉链存储结构中有n+1个空指针域,利用这些空指针域存放在某种遍历次序下该结点的前驱结点和后继结点的指针,这些指针被称为线索,加上线索的二叉树称为线索二叉树。
结点结构如下:

其中:
lTag为0时,lChild指向该结点的左孩子,为1时指向该结点的前驱
rTag为0时,rChild指向该结点的右孩子,为1时指向该结点的后继。
线索二叉树的结构图为:图中蓝色虚线为前驱,红色虚线为后继
代码如下:
public class ThreadedBinaryTree<E> {private TBTreeNode root;private int size; // 大小 private TBTreeNode pre; // 线索化的时候保存前驱 class TBTreeNode {E element;boolean lTag; //false表示指向孩子结点,true表示指向前驱或后继的线索boolean rTag;TBTreeNode lChild;TBTreeNode rChild;public TBTreeNode(E element) {this.element = element;}}public ThreadedBinaryTree(E[] data) {this.pre = null; this.size = data.length; this.root = createTBTree(data, 1);}//构建二叉树public TBTreeNode createTBTree(E[] data, int index) { if (index > data.length){ return null; } TBTreeNode node = new TBTreeNode(data[index - 1]); TBTreeNode left = createTBTree(data, 2 * index); TBTreeNode right = createTBTree(data, 2 * index + 1); node.lChild = left; node.rChild = right; return node; } /** * 将二叉树线索化 */ public void inThreading(TBTreeNode node) { if (node != null) { inThreading(node.lChild); // 线索化左孩子 if (node.lChild == null) { // 左孩子为空 node.lTag = true; // 将左孩子设置为线索 node.lChild = pre; } if (pre != null && pre.rChild == null) { // 右孩子为空 pre.rTag = true; pre.rChild = node; } pre = node; inThreading(node.rChild); // 线索化右孩子 } } /** * 中序遍历线索二叉树 */ public void inOrderTraverseWithThread(TBTreeNode node) {while(node != null) {while(!node.lTag) { //找到中序遍历的第一个结点node = node.lChild;}System.out.print(node.element + " "); while(node.rTag && node.rChild != null) { //若rTag为true,则打印后继结点node = node.rChild;System.out.print(node.element + " "); }node = node.rChild;}} /** * 中序遍历,线索化后不能使用*/ public void inOrderTraverse(TBTreeNode node) { if(node == null)return;inOrderTraverse(node.lChild); System.out.print(node.element + " "); inOrderTraverse(node.rChild); } public TBTreeNode getRoot() { return root;}public static void main(String[] args) {Character[] data = {'A','B','C','D','E','F','G','H','I','J'};ThreadedBinaryTree<Character> tbt = new ThreadedBinaryTree<>(data);tbt.inOrderTraverse(tbt.getRoot());System.out.println();tbt.inThreading(tbt.getRoot());tbt.inOrderTraverseWithThread(tbt.getRoot());}
}
线索二叉树充分利用了空指针域的空间,提高了遍历二叉树的效率。
五、总结
到此,树的知识基本总结完了,这一节开头讲了树的一些基本概念,重点介绍了树的三种不同的存储方法:双亲表示法、孩子表示法和孩子兄弟表示法。由兄弟表示法引入了一种特殊的树:二叉树,并详细介绍了它的性质、不同结构的实现方法和遍历方法。最后介绍了线索二叉树的实现方法。
相关文章:

数据结构与算法(四):树结构
前面讲到的顺序表、栈和队列都是一对一的线性结构,这节讲一对多的线性结构——树。「一对多」就是指一个元素只能有一个前驱,但可以有多个后继。 一、基本概念 树(tree)是n(n>0)个结点的有穷集。n0时称…...
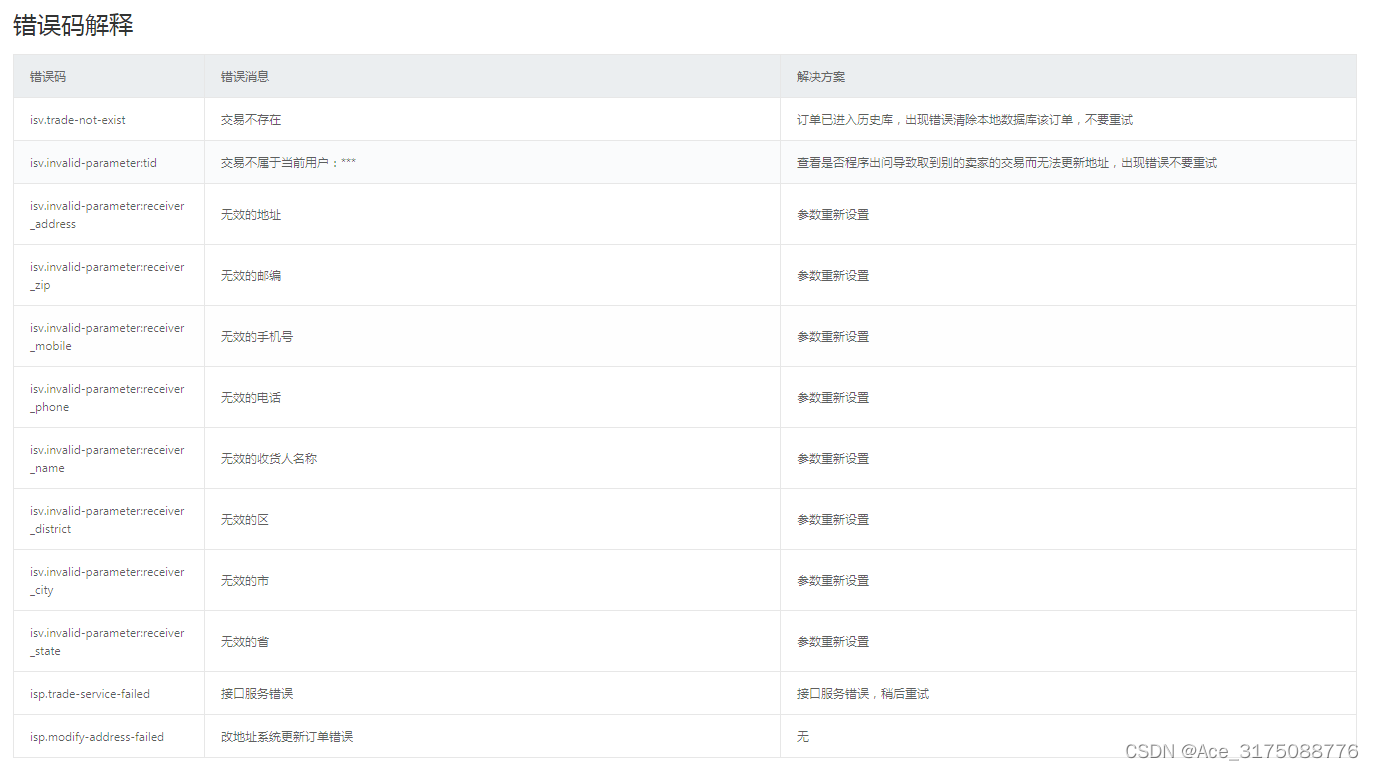
taobao.trade.shippingaddress.update( 更改交易的收货地址 )
¥开放平台免费API必须用户授权 只能更新一笔交易里面的买家收货地址 只能更新发货前(即买家已付款,等待卖家发货状态)的交易的买家收货地址 更新后的发货地址可以通过taobao.trade.fullinfo.get查到 参数中所说的字节为GBK编码的&…...
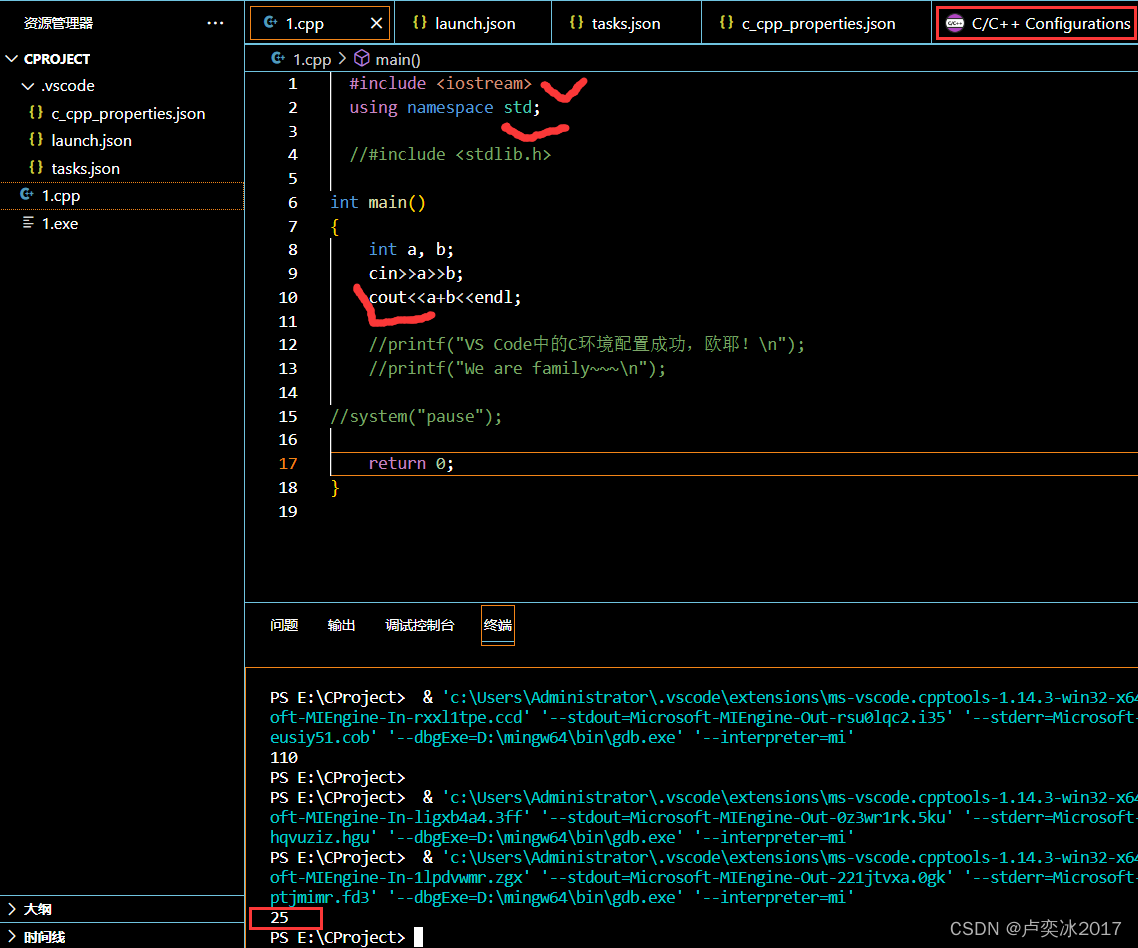
VS Code安装及(C/C++)环境配置(Windows系统)
参考资料2份: 从零开始的vscode安装及环境配置教程(C/C)(Windows系统)_光中影zone的博客-CSDN博客_vscode运行配置https://blog.csdn.net/qq_45807140/article/details/112862592 VSCode配置C/C环境 - 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/87864677 五…...
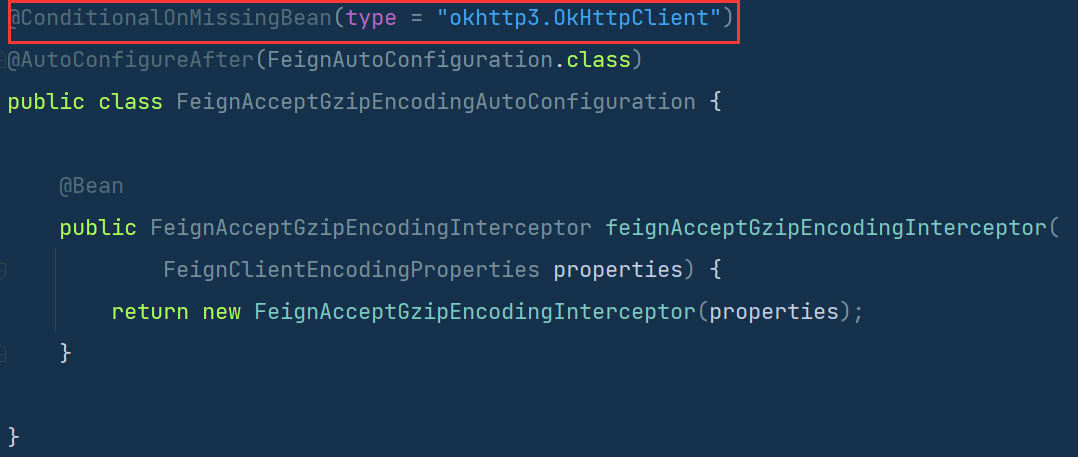
【Spring Cloud Alibaba】006-OpenFeign
【Spring Cloud Alibaba】006-OpenFeign 文章目录【Spring Cloud Alibaba】006-OpenFeign一、概述1、Java 项目实现接口调用的方法HttpclientOkhttpHttpURLConnectionRestTemplate WebClient2、Feign 概述二、Spring Cloud Alibaba 快速整合 OpenFeign1、添加依赖2、启动类加注…...

挚文集团短期内不适合投资,长期内看好
来源:猛兽财经 作者:猛兽财经 挚文集团(MOMO)在新闻稿中称自己是“中国在线社交和娱乐领域的领军企业”。 该公司旗下的陌陌是中国“陌生人社交网络”移动应用类别的领导者,并在2022年9月拥有超过1亿的月活跃用户。探…...

clion开发的常用快捷键以及gitcrlf的问题
前段报错:git config core.autocrlf false 然后删除app目录下的文件,除了.git文件夹然后 git bash ,执行 git reset --hardclion常用快捷键:Double shift 搜索文件F9调试F9运行到断点Ctrl F8 打断点F7单步步入Shift F8 单步跳出F8执行下一行代…...

LeetCode 格雷编码问题
格雷编码格雷编码的定义格雷编码的码表LeetCode 89. 格雷编码实例思路与代码思路一:找规律代码一代码二思路二:与自然数之间的关系(你必须知道,这个规律要去百度才知道)代码一LeetCode 1238. 循环码排列实例思路与代码…...

java生成html文件输出到指定位置
String fileName "filename.html";StringBuilder sb new StringBuilder();// 使用StringBuilder 构建HTML文件sb.append("<html>\n");sb.append("<head>\n");sb.append("<title>HTML File</title>\n");sb.a…...

华为OD机试用Python实现 -【微服务的集成测试】(2023-Q1 新题)
华为OD机试300题大纲 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。 华为 OD 清单查看地址:blog.csdn.net/hihell/category_12199275.html 华为OD详细说明:https://dream.blog.csdn.net/article/details/128980730 微服务的集成测试…...
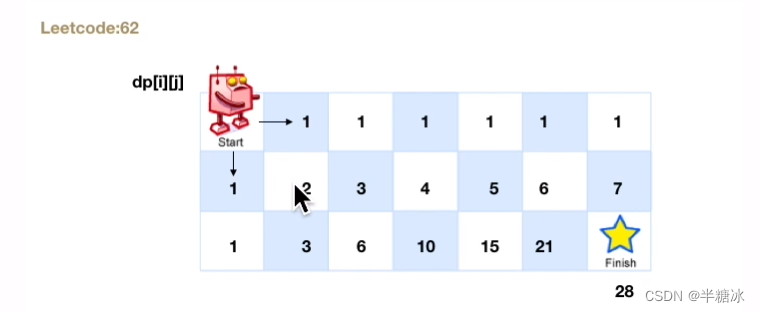
js版 力扣 62. 不同路径
一、题目描述 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。问总共有多少条不同的路径࿱…...

Qt音视频开发16-通用悬浮按钮工具栏的设计
一、前言 通用悬浮按钮工具栏这个功能经过了好几个版本的迭代,一开始设计的时候是写在视频控件widget窗体中,当时功能简单就放一排按钮在顶部悬浮widget中就好,随着用户需求的变化,用户需要自定义悬浮条的要求越发强烈࿰…...

商品比价API使用说明
商品数据分析 国内最早的比价搜索平台,专注于电商大数据的分析,有10年技术和数据沉淀。 公司自主研发的爬虫、搜索引擎、分布式计算等技术, 实现了对海量电商数据的及时监测、清洗和统计。 数据丰富 详细使用api 数据采集维度ÿ…...

基于 TensorFlow 的植物识别教程
首先,需要准备一些训练数据集。这些数据集应该包含两个文件夹:一个用于训练数据,另一个用于测试数据。每个文件夹应该包含子文件夹,每个子文件夹对应一个植物的种类,并包含该植物的图像。接下来,我们需要使…...

渗透测试之主机探测存活性实验
渗透测试之主机探测存活性实验实验目的一、实验原理1.1 TCP/IP协议1. TCP2. IP1.2 Ping的原理二、实验环境2.1 操作机器2.2 实验工具三、实验步骤1. 学会使用ping命令2. 使用Nmap进行多种方式的探测总结实验目的 熟悉TCP/IP协议、Ping命令基本概念学习nmap、SuperScan扫描方式…...
好用的idea插件leetcode editor【详细安装指南】
如果你和我一样存在着如下困扰: 上班想摸鱼刷leetcode,但是直接打开leetcode界面太扎眼了或者为leetcode刷题不可以debug而发愁 那今天分享的一款IDEA插件可以统统解决上述问题,插件名字叫leetcode editor,你可以直接在plugins中…...

二氧化碳地质封存技术应用前景及模型构建实践方法与讨论
2022年七月七日,工业和信息化部、发展改革委、生态环境部关于印发工业领域碳达峰实施方案的通知落地。全国各省份积极响应,纷纷出台地方指导文件,标志着我国碳减排事业的全面铺开。二氧化碳地质封存技术作为实现我国“双碳”目标的重要一环&a…...
STM32开发(12)----CubeMX配置WWDG
CubeMX配置窗口看门狗(WWDG)前言一、窗口看门狗的介绍二、实验过程1.STM32CubeMX配置窗口看门狗2.代码实现3.硬件连接4.实验结果总结前言 本章介绍使用STM32CubeMX对窗口看门狗定时器进行配置的方法。门狗本质上是一个定时器,提供了更高的安…...
JVM18运行时参数
4. JVM 运行时参数 4.1. JVM 参数选项 官网地址:https://docs.oracle.com/javase/8/docs/technotes/tools/windows/java.html 4.1.1. 类型一:标准参数选项 > java -help 用法: java [-options] class [args...](执行类)或 java [-options] -jar …...
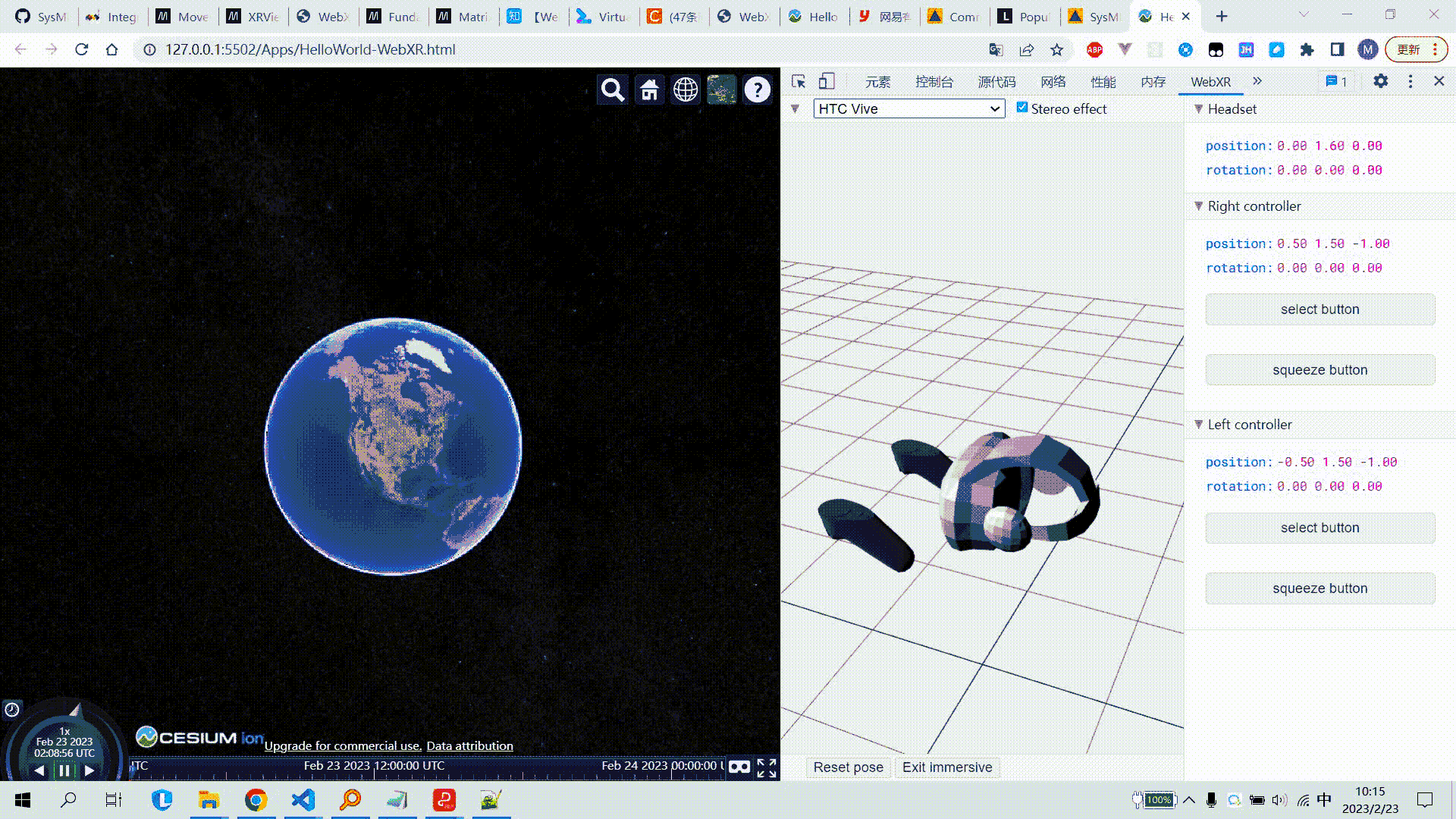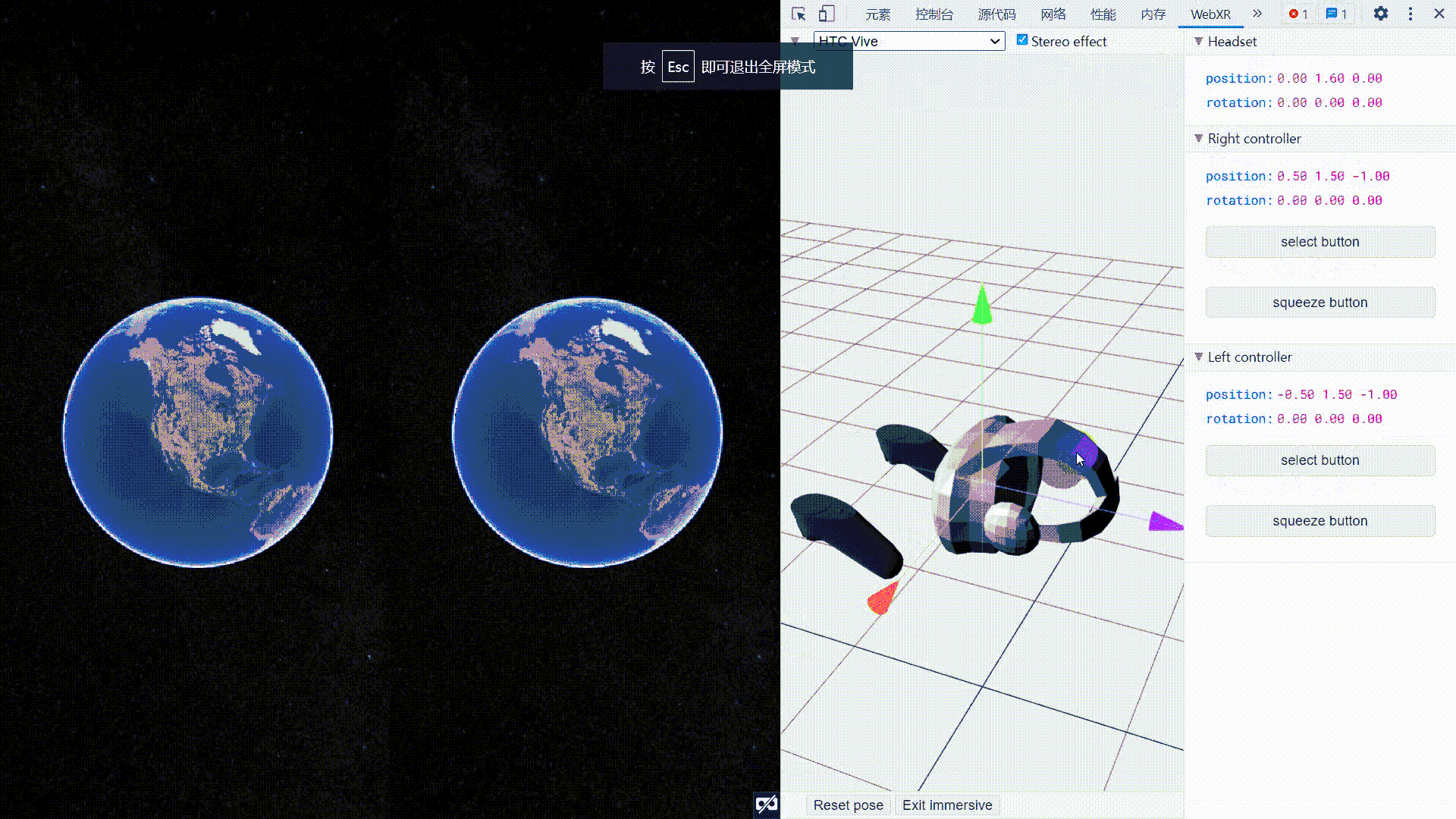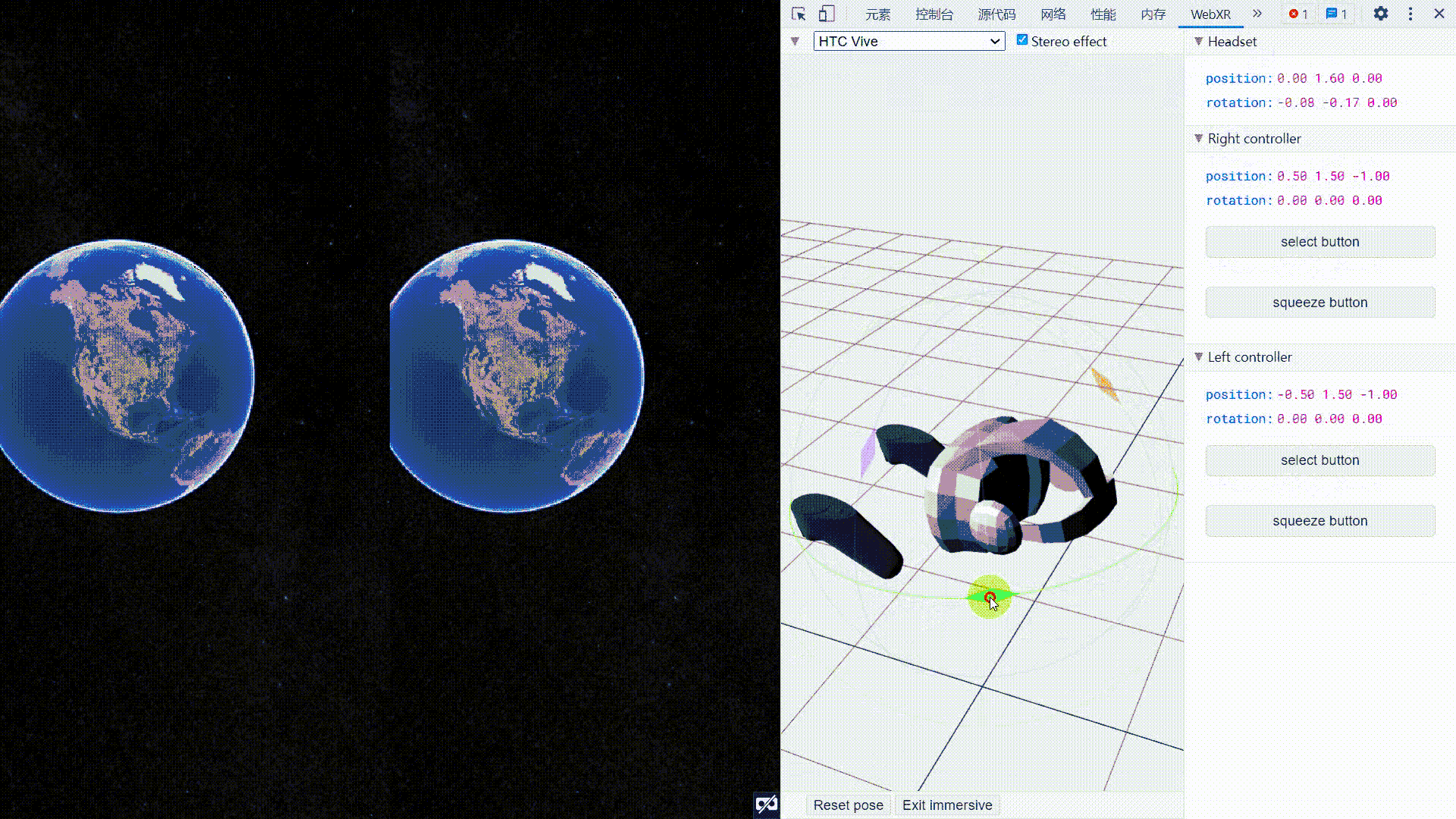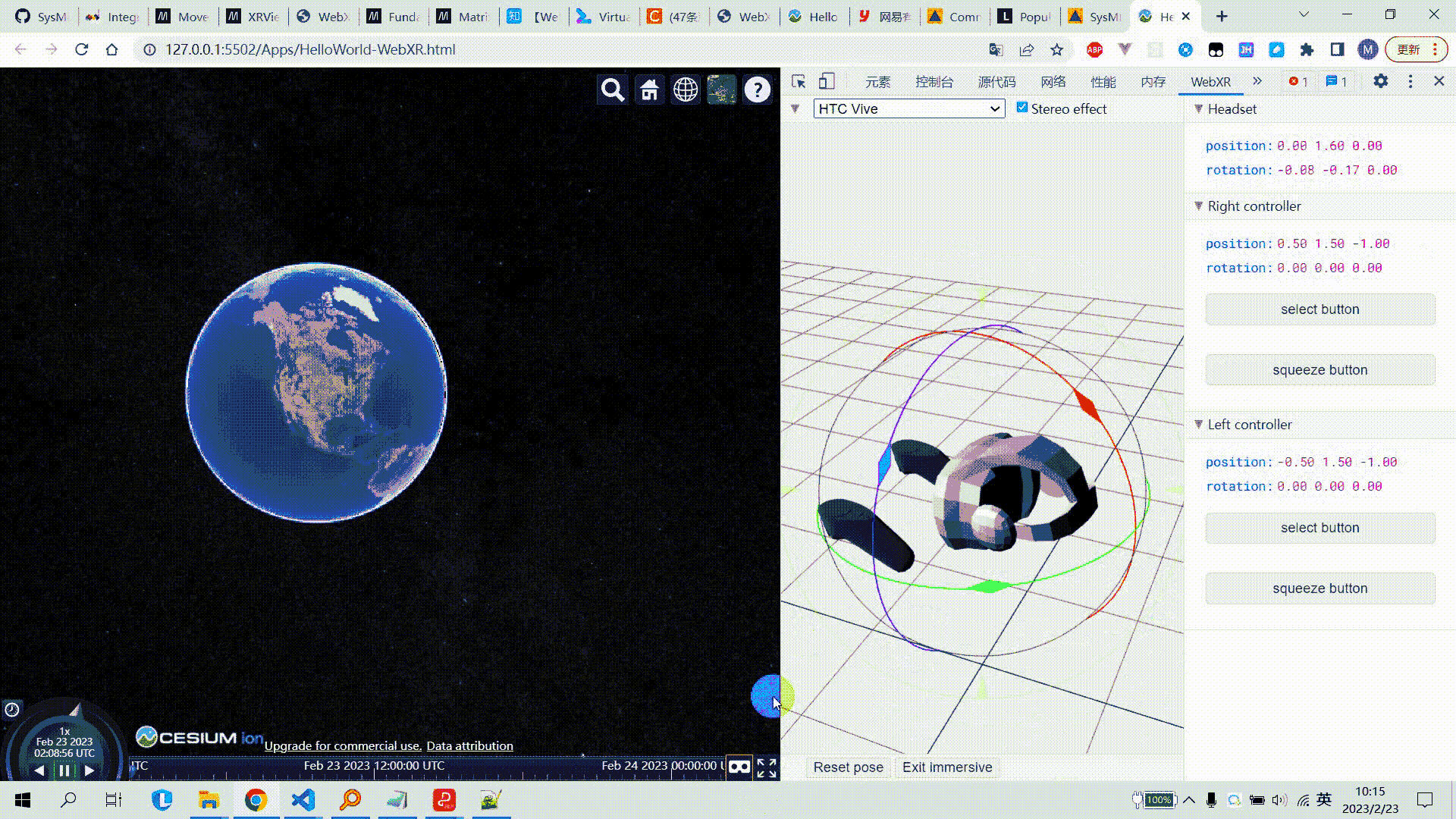
Cesium集成WebXR_连接VR设备
Cesium集成WebXR 文章目录Cesium集成WebXR1. 需求2. 技术基础2.1 WebGL2.2 WebXR2.3 其他3. 示例代码4. 效果图5. 参考链接1. 需求 通过WebXR接口,将浏览器端连接到VR头盔,实现在VR头盔中浏览Cesium场景,并可将头盔旋转的操作同步映射为场景…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

