小白入门pytorch(一)
- 本文为小白入门Pytorch中的学习记录博客
小白入门pytorch 基础知识
导入torch,查看torch版本
import torch
print(torch.__version__)
输出结果:
1.12.1+cu113
张量
在pytorch中,张量(tensor)是最基本的数据结构。
- 零维张量—》标量,维度为0,一个单独的值,只有大小,没有方向
- 一维张量—》向量,维度为1
- 二维张量—》矩阵,维度为2
- 三维张量—》三维数组,维度为3
零维张量
tensor = torch.tensor(10)
print("tensor的形状", tensor.shape)
print("tensor的值", tensor)
输出结果:
tensor的形状 torch.Size([])
tensor的值 tensor(10)
一维张量
tensor = torch.tensor([1, 2, 3, 4, 5])
print("tensor的形状", tensor.shape)
print("tensor的值", tensor)
输出结果:
tensor的形状 torch.Size([5])
tensor的值 tensor([1, 2, 3, 4, 5])
二维张量
tensor = torch.tensor([[1, 2, 3], [4, 5, 6]])
print("tensor的形状", tensor.shape)
print( tensor)
输出结果:
tensor的形状 torch.Size([2, 3])
tensor([[1, 2, 3],[4, 5, 6]])
torch.Size([2, 3])中的[2, 3]是代表2行,3列
三维张量
tensor = torch.tensor([[[1, 2],[3, 4]], [[5, 6],[7, 8]]])
print(tensor.shape)
print(tensor)
输出结果:
torch.Size([2, 2, 2])
tensor([[[1, 2],[3, 4]],[[5, 6],[7, 8]]])
torch.Size([2, 2, 2]):包含两个二维矩阵,每个二维矩阵的形状是2行2列
张量的操作
创建张量
列表创建
tensor = torch.tensor([1, 2])
tensor
输入结果:
tensor([1, 2])
元组创建
tensor = torch.tensor((1, 2))
tensor
输出结果:
tensor([1, 2])
通过Numpy创建
import numpy as np
data = np.array([1, 2])
tensor = torch.tensor(data)
tensor
输出结果:
tensor([1, 2], dtype=torch.int32)
创建一个具有特定数据类型的张量
tensor = torch.tensor([1, 2, 3], dtype=torch.float32)
print(tensor)
print(tensor.dtype)
输出结果:
tensor([1., 2., 3.])
torch.float32
创建全零向量
zeros_tensor = torch.zeros([2, 3]) # 创建一个2行3列的全零张量
print(zeros_tensor.shape)
zeros_tensor
输出结果:
torch.Size([2, 3])
tensor([[0., 0., 0.],[0., 0., 0.]])
torch.zeros()全零张量的函数
全1张量
ones_tensor = torch.ones((2, 3)) # 创建一个2行3列的全1张量
print(ones_tensor.shape)
ones_tensor
输出结果:
torch.Size([2, 3])
tensor([[1., 1., 1.],[1., 1., 1.]])
torch.ones()全1张量的函数
随机张量
rand_tensor = torch.rand((2, 3)) # 创建一个2行3列随机张量, torch.rand()函数将生成一个(0,1)范围内均匀分布的随机张量
print(rand_tensor.shape)
print(rand_tensor)
输出结果:
torch.Size([2, 3])
tensor([[0.4723, 0.6665, 0.7575],[0.8820, 0.1854, 0.1162]])
张量索引和切片
使用索引和切片操作来访问张量中的特定元素或子张量
tensor = torch.tensor([[1, 2, 3],[4, 5, 6],[7, 8, 9]])
print(tensor)
输出结果:
tensor([[1, 2, 3],[4, 5, 6],[7, 8, 9]])
访问第一个元素
# 访问第一个元素
print(tensor[0, 0])
切片操作
# 切片操作
tensor[:, 1] # 逗号两边的数字,左边是控制行,右边是控制列
输出结果:
tensor([2, 5, 8])
# 取第一行和第三行的第一列和第三列的元素
tensor[::2, ::2]
输出结果:
tensor([[1, 3],[7, 9]])
张量GPU加速
# 创建一个形状为(2, 2)的张量
tensor = torch.tensor([[1, 2], [3, 4]])
tensor = tensor.to('cuda') # 将张量转移到gpu上
tensor
输出结果:
tensor([[1, 2],[3, 4]], device='cuda:0')
张量转移到CPU上
tensor = tensor.to('cpu')
print(tensor)
输出结果:
tensor([[1, 2],[3, 4]])
张量运算
- 可以对张量执行各种数学运算和操作,如加法、减法、乘法、除法、矩阵乘法等
# 创建两个张量
tensor1 = torch.tensor([1, 2, 3])
tensor2 = torch.tensor([3, 3, 3])
# 加法
result = tensor1 + tensor2
print("加法的结果", result)
# 减法
result = tensor1 - tensor2
print("减法的结果", result)
# 乘法
result = tensor1 * tensor2
print("乘法的结果", result)
# 除法
result = tensor1 / tensor2
print("除法的结果", result)
加法的结果 tensor([4, 5, 6])
减法的结果 tensor([-2, -1, 0])
乘法的结果 tensor([3, 6, 9])
除法的结果 tensor([0.3333, 0.6667, 1.0000])
- 张量与标量相加,与标量相乘
# 张量与标量相加
tensor1 = torch.tensor([1, 2, 3])
temp_var = 1
result = tensor1 + temp_var
print("张量与标量相加结果", result)# 张量与标量相乘
tensor1 = torch.tensor([1, 2, 3])
temp_var = 2
result = tensor1 * temp_var
print("张量与标量相乘结果", result)
输出结果:
张量与标量相加结果 tensor([2, 3, 4])
张量与标量相乘结果 tensor([2, 4, 6])
张量的形状转换
tensor = torch.tensor([[1, 2, 3], [4, 5, 6]]) # 2行3列
print("原来的张量\n",tensor)
tensor = tensor.reshape(3, 2) # 3行2列
print("变换后的张量\n", tensor)
输出结果:
原来的张量tensor([[1, 2, 3],[4, 5, 6]])
变换后的张量tensor([[1, 2],[3, 4],[5, 6]])
# 改变张量的形状(与reshape功能相同)
tensor = torch.tensor([[1, 2, 3],[4, 5, 6]]) # 2行3列
print("原来的张量\n", tensor)
tensor = tensor.view(3, 2) # 3行2列
print("变换后的向量\n", tensor)
原来的张量tensor([[1, 2, 3],[4, 5, 6]])
变换后的向量tensor([[1, 2],[3, 4],[5, 6]])
获取张量的数值
tensor = torch.randn(1) # 如果张量中仅有一个元素,可用item
print(tensor)
print(tensor.item())
输出结果:
tensor([-0.5515])
-0.5514923930168152
张量转化为数组
tensor = torch.tensor([[1, 2, 3],[4, 5, 6],[7, 8, 9]])
array = tensor.numpy() # 将张量转化为Numpy数组
print(array)
输出结果:
[[1 2 3][4 5 6][7 8 9]]
张量转化为列表
tensor = torch.tensor([[1, 2, 3],[4, 5, 6]])
# 将张量转化为列表
tensor_list = tensor.tolist()
tensor_list
输出结果:
[[1, 2, 3], [4, 5, 6]]
自动求导原理
- 自动求导是一个关键的功能,它允许我们自动计算梯度,从而计算反向传播和优化
计算图
- 计算图是一个有向无环图,它描述了计算过程中的操作和数据之间的依赖关系。在pytorch中,每个计算图由一系列的节点和边组成。节点表示操作(例如加法、乘法)或者数据,边表示数据的流动方向。计算图分为两个阶段:前向传播 和 反向传播
- 前向传播:在前向传播阶段,计算图从输入节点开始,按照节点之间的依赖关系依次进行计算,直到到达输出节点。在这个过程中,每个节点将计算并传递输出给下一个依赖节点
- 反向传播:在反向传播阶段,计算图从输出节点开始,沿着边的反方向传播梯度。在这个过程中,每个节点根据链式法则将梯度传递给输入节点,以便计算它们的梯度
- 通过构建计算图,Pytorch可以记录整个计算过程,并在需要时自动计算梯度。这使得我们可以轻松地进行方向传播,并在优化算法中使用梯度信息。
梯度
- 梯度,它表示了函数在某一点的变化率。在Pytorch中,计算梯度是一项关键操作,它允许我们通过反向传播算法有效地更新模型参数。
- 梯度是一个向量,其方向是指向函数值增长最快的方向,而其大小表示函数值的变化率。在深度学习中,我们通常希望最小化损失函数,因此梯度的反方向更新模型参数,以逐步降低损失值
- Pytorch中的torch.tensor类是Pytorch的核心数据结构,同时也是计算梯度的关键。每个张量都有一个requires_grad,默认为False。如果我们希望计算某个张量的梯度,需要将requires_grad设置为True,那么就会开始追踪在该变量上的所有操作,而完成计算后,可以调用.backward()并自动计算所有的梯度,得到的梯度都保存在属性.grad中。
- 调用.detach()方法分离出计算的历史,可以停止一个tensor变量继续追踪其历史信息,同时也防止未来的计算会被追踪。
- 如果希望防止追踪历史(以及使用内存),可以将代码放在with torch.no_grad():内,这个做法在使用一个模型进行评估的时候非常有用,因为模型包含一些带有requires_grad=True的训练参数,但实际上并不需要它们的梯度信息
- 对于autograd的实现,还有一个类也是非常重要的–Function
- Tensor和Function两个类是有关联并建立了一个非循环的图,可以编码成一个完整的计算记录,每个Tensor变量都带有属性.grad_fn,该属性引用了创建了这个变量的Function
梯度计算过程
- 在pytorch中,计算梯度的过程中主要分为以下几个步骤:
创建张量并设置requires_grad=True,首先,要创建一个张量,并将requires_grad属性设置为True, 以便pytorch跟踪其梯度
x = torch.tensor([2.0, 3.0], requires_grad=True)
定义计算图:接下来,使用创建的张量进行计算,可以使用任何pytorch支持的函数、操作和模型
y = x**2 + 3*x + 1
计算梯度:一旦我们得到了最终的输出张量,我们可以使用backward()方法自动计算梯度
y.sum().backward()
获取梯度值:通过访问张量的grad属性,我们可以获得计算得到的梯度值
print(x.grad)
输出结果:
tensor([7., 9.])
梯度计算示例
线性回归
import torch # 创建训练数据
x_train = torch.tensor([[1.0], [2.0], [3.0]])
y_train = torch.tensor([[2.0], [4.0], [6.0]])#定义模型参数
w = torch.tensor([[0.0]], requires_grad=True)
b = torch.tensor([[0.0]], requires_grad=True)# 定义模型
def linear_regression(x):return torch.matmul(x, w) + b# 定义损失函数
def loss_fn(y_pred, y):return torch.mean((y_pred - y)**2)# 优化器
optimizer = torch.optim.SGD([w, b], lr=0.01)# 训练模型for epoch in range(100):# 前向传播y_pred = linear_regression(x_train)# 计算损失loss = loss_fn(y_pred, y_train)print(loss)# 反向传播loss.backward()# 更新参数optimizer.step()# 清零梯度optimizer.zero_grad()打印loss的结果看一下
tensor(18.6667, grad_fn=<MeanBackward0>)
tensor(14.7710, grad_fn=<MeanBackward0>)
tensor(11.6915, grad_fn=<MeanBackward0>)
tensor(9.2573, grad_fn=<MeanBackward0>)
tensor(7.3332, grad_fn=<MeanBackward0>)
tensor(5.8121, grad_fn=<MeanBackward0>)
tensor(4.6098, grad_fn=<MeanBackward0>)
tensor(3.6593, grad_fn=<MeanBackward0>)
tensor(2.9079, grad_fn=<MeanBackward0>)
tensor(2.3139, grad_fn=<MeanBackward0>)
tensor(1.8443, grad_fn=<MeanBackward0>)
tensor(1.4730, grad_fn=<MeanBackward0>)
tensor(1.1795, grad_fn=<MeanBackward0>)
tensor(0.9474, grad_fn=<MeanBackward0>)
tensor(0.7639, grad_fn=<MeanBackward0>)
tensor(0.6187, grad_fn=<MeanBackward0>)
tensor(0.5039, grad_fn=<MeanBackward0>)
tensor(0.4131, grad_fn=<MeanBackward0>)
tensor(0.3412, grad_fn=<MeanBackward0>)
tensor(0.2844, grad_fn=<MeanBackward0>)
tensor(0.2393, grad_fn=<MeanBackward0>)
tensor(0.2037, grad_fn=<MeanBackward0>)
tensor(0.1754, grad_fn=<MeanBackward0>)
tensor(0.1530, grad_fn=<MeanBackward0>)
tensor(0.1352, grad_fn=<MeanBackward0>)
tensor(0.1211, grad_fn=<MeanBackward0>)
tensor(0.1099, grad_fn=<MeanBackward0>)
tensor(0.1009, grad_fn=<MeanBackward0>)
tensor(0.0938, grad_fn=<MeanBackward0>)
tensor(0.0881, grad_fn=<MeanBackward0>)
tensor(0.0835, grad_fn=<MeanBackward0>)
tensor(0.0798, grad_fn=<MeanBackward0>)
tensor(0.0769, grad_fn=<MeanBackward0>)
tensor(0.0744, grad_fn=<MeanBackward0>)
tensor(0.0724, grad_fn=<MeanBackward0>)
tensor(0.0708, grad_fn=<MeanBackward0>)
tensor(0.0695, grad_fn=<MeanBackward0>)
tensor(0.0683, grad_fn=<MeanBackward0>)
tensor(0.0674, grad_fn=<MeanBackward0>)
tensor(0.0665, grad_fn=<MeanBackward0>)
tensor(0.0658, grad_fn=<MeanBackward0>)
tensor(0.0652, grad_fn=<MeanBackward0>)
tensor(0.0646, grad_fn=<MeanBackward0>)
tensor(0.0641, grad_fn=<MeanBackward0>)
tensor(0.0637, grad_fn=<MeanBackward0>)
tensor(0.0632, grad_fn=<MeanBackward0>)
tensor(0.0628, grad_fn=<MeanBackward0>)
tensor(0.0625, grad_fn=<MeanBackward0>)
tensor(0.0621, grad_fn=<MeanBackward0>)
tensor(0.0618, grad_fn=<MeanBackward0>)
tensor(0.0614, grad_fn=<MeanBackward0>)
tensor(0.0611, grad_fn=<MeanBackward0>)
tensor(0.0608, grad_fn=<MeanBackward0>)
tensor(0.0605, grad_fn=<MeanBackward0>)
tensor(0.0602, grad_fn=<MeanBackward0>)
tensor(0.0599, grad_fn=<MeanBackward0>)
tensor(0.0596, grad_fn=<MeanBackward0>)
tensor(0.0593, grad_fn=<MeanBackward0>)
tensor(0.0590, grad_fn=<MeanBackward0>)
tensor(0.0587, grad_fn=<MeanBackward0>)
tensor(0.0584, grad_fn=<MeanBackward0>)
tensor(0.0581, grad_fn=<MeanBackward0>)
tensor(0.0578, grad_fn=<MeanBackward0>)
tensor(0.0576, grad_fn=<MeanBackward0>)
tensor(0.0573, grad_fn=<MeanBackward0>)
tensor(0.0570, grad_fn=<MeanBackward0>)
tensor(0.0567, grad_fn=<MeanBackward0>)
tensor(0.0565, grad_fn=<MeanBackward0>)
tensor(0.0562, grad_fn=<MeanBackward0>)
tensor(0.0559, grad_fn=<MeanBackward0>)
tensor(0.0557, grad_fn=<MeanBackward0>)
tensor(0.0554, grad_fn=<MeanBackward0>)
tensor(0.0551, grad_fn=<MeanBackward0>)
tensor(0.0549, grad_fn=<MeanBackward0>)
tensor(0.0546, grad_fn=<MeanBackward0>)
tensor(0.0543, grad_fn=<MeanBackward0>)
tensor(0.0541, grad_fn=<MeanBackward0>)
tensor(0.0538, grad_fn=<MeanBackward0>)
tensor(0.0536, grad_fn=<MeanBackward0>)
tensor(0.0533, grad_fn=<MeanBackward0>)
tensor(0.0530, grad_fn=<MeanBackward0>)
tensor(0.0528, grad_fn=<MeanBackward0>)
tensor(0.0525, grad_fn=<MeanBackward0>)
tensor(0.0523, grad_fn=<MeanBackward0>)
tensor(0.0520, grad_fn=<MeanBackward0>)
tensor(0.0518, grad_fn=<MeanBackward0>)
tensor(0.0515, grad_fn=<MeanBackward0>)
tensor(0.0513, grad_fn=<MeanBackward0>)
tensor(0.0510, grad_fn=<MeanBackward0>)
tensor(0.0508, grad_fn=<MeanBackward0>)
tensor(0.0505, grad_fn=<MeanBackward0>)
tensor(0.0503, grad_fn=<MeanBackward0>)
tensor(0.0501, grad_fn=<MeanBackward0>)
tensor(0.0498, grad_fn=<MeanBackward0>)
tensor(0.0496, grad_fn=<MeanBackward0>)
tensor(0.0493, grad_fn=<MeanBackward0>)
tensor(0.0491, grad_fn=<MeanBackward0>)
tensor(0.0489, grad_fn=<MeanBackward0>)
tensor(0.0486, grad_fn=<MeanBackward0>)
tensor(0.0484, grad_fn=<MeanBackward0>)
反向传播
反向传播原理
- 在深度学习中,我们通常使用梯度下降法来最小化损失函数,从而训练神经网络模型。而反向传播是计算损失函数对模型参数梯度的一种有效方法。通过计算参数梯度,我们可以梯度的反方向更新参数,使得模型的预测结果逐渐接近真实标签
- 反向传播的几个步骤:
- 前向传播:将输入样本通过神经网络的前向计算过程,计算出预测结果
- 计算损失:将预测结果与真实标签进行比较,并计算损失函数的值
- 反向传播梯度:根据损失函数的值,计算损失函数对模型参数的梯度
- 参数更新:根据参数的梯度和优化算法的规则,更新模型的参数
反向传播示例
import torch
import torch.nn as nn
import torch.optim as optimclass LinearRegression(nn.Module):def __init__(self):super(LinearRegression, self).__init__()self.linear = nn.Linear(1, 1) # 输入维度为1, 输出维度为1def forward(self, x):return self.linear(x)
# 创建模型的实例、定义损失函数和优化器
model = LinearRegression()
criterion = nn.MSELoss() # 均方误差损失函数
optimizer = optim.SGD(model.parameters(), lr=0.01)
# 生成样本数据,并进行训练
x_train = torch.tensor([[1.0],[2.0],[3.0],[4.0]])
y_train = torch.tensor([[2.0],[4.0],[6.0],[8.0]])# 训练模型
for epoch in range(100):# 梯度清零optimizer.zero_grad() # 前向传播y_pred = model(x_train)# 计算损失loss = criterion(y_pred, y_train)# 反向传播loss.backward()# 参数更新optimizer.step()print(loss)
输出损失值:
tensor(30.6108, grad_fn=<MseLossBackward0>)
tensor(21.2626, grad_fn=<MseLossBackward0>)
tensor(14.7759, grad_fn=<MseLossBackward0>)
tensor(10.2748, grad_fn=<MseLossBackward0>)
tensor(7.1515, grad_fn=<MseLossBackward0>)
tensor(4.9841, grad_fn=<MseLossBackward0>)
tensor(3.4801, grad_fn=<MseLossBackward0>)
tensor(2.4364, grad_fn=<MseLossBackward0>)
tensor(1.7120, grad_fn=<MseLossBackward0>)
tensor(1.2093, grad_fn=<MseLossBackward0>)
tensor(0.8603, grad_fn=<MseLossBackward0>)
tensor(0.6181, grad_fn=<MseLossBackward0>)
tensor(0.4498, grad_fn=<MseLossBackward0>)
tensor(0.3330, grad_fn=<MseLossBackward0>)
tensor(0.2518, grad_fn=<MseLossBackward0>)
tensor(0.1953, grad_fn=<MseLossBackward0>)
tensor(0.1560, grad_fn=<MseLossBackward0>)
tensor(0.1286, grad_fn=<MseLossBackward0>)
tensor(0.1095, grad_fn=<MseLossBackward0>)
tensor(0.0961, grad_fn=<MseLossBackward0>)
tensor(0.0866, grad_fn=<MseLossBackward0>)
tensor(0.0800, grad_fn=<MseLossBackward0>)
tensor(0.0753, grad_fn=<MseLossBackward0>)
tensor(0.0718, grad_fn=<MseLossBackward0>)
tensor(0.0694, grad_fn=<MseLossBackward0>)
tensor(0.0675, grad_fn=<MseLossBackward0>)
tensor(0.0661, grad_fn=<MseLossBackward0>)
tensor(0.0651, grad_fn=<MseLossBackward0>)
tensor(0.0642, grad_fn=<MseLossBackward0>)
tensor(0.0635, grad_fn=<MseLossBackward0>)
tensor(0.0629, grad_fn=<MseLossBackward0>)
tensor(0.0623, grad_fn=<MseLossBackward0>)
tensor(0.0619, grad_fn=<MseLossBackward0>)
tensor(0.0614, grad_fn=<MseLossBackward0>)
tensor(0.0610, grad_fn=<MseLossBackward0>)
tensor(0.0606, grad_fn=<MseLossBackward0>)
tensor(0.0602, grad_fn=<MseLossBackward0>)
tensor(0.0598, grad_fn=<MseLossBackward0>)
tensor(0.0595, grad_fn=<MseLossBackward0>)
tensor(0.0591, grad_fn=<MseLossBackward0>)
tensor(0.0587, grad_fn=<MseLossBackward0>)
tensor(0.0584, grad_fn=<MseLossBackward0>)
tensor(0.0580, grad_fn=<MseLossBackward0>)
tensor(0.0577, grad_fn=<MseLossBackward0>)
tensor(0.0573, grad_fn=<MseLossBackward0>)
tensor(0.0570, grad_fn=<MseLossBackward0>)
tensor(0.0566, grad_fn=<MseLossBackward0>)
tensor(0.0563, grad_fn=<MseLossBackward0>)
tensor(0.0560, grad_fn=<MseLossBackward0>)
tensor(0.0556, grad_fn=<MseLossBackward0>)
tensor(0.0553, grad_fn=<MseLossBackward0>)
tensor(0.0550, grad_fn=<MseLossBackward0>)
tensor(0.0546, grad_fn=<MseLossBackward0>)
tensor(0.0543, grad_fn=<MseLossBackward0>)
tensor(0.0540, grad_fn=<MseLossBackward0>)
tensor(0.0537, grad_fn=<MseLossBackward0>)
tensor(0.0533, grad_fn=<MseLossBackward0>)
tensor(0.0530, grad_fn=<MseLossBackward0>)
tensor(0.0527, grad_fn=<MseLossBackward0>)
tensor(0.0524, grad_fn=<MseLossBackward0>)
tensor(0.0521, grad_fn=<MseLossBackward0>)
tensor(0.0518, grad_fn=<MseLossBackward0>)
tensor(0.0515, grad_fn=<MseLossBackward0>)
tensor(0.0512, grad_fn=<MseLossBackward0>)
tensor(0.0508, grad_fn=<MseLossBackward0>)
tensor(0.0505, grad_fn=<MseLossBackward0>)
tensor(0.0502, grad_fn=<MseLossBackward0>)
tensor(0.0499, grad_fn=<MseLossBackward0>)
tensor(0.0496, grad_fn=<MseLossBackward0>)
tensor(0.0493, grad_fn=<MseLossBackward0>)
tensor(0.0491, grad_fn=<MseLossBackward0>)
tensor(0.0488, grad_fn=<MseLossBackward0>)
tensor(0.0485, grad_fn=<MseLossBackward0>)
tensor(0.0482, grad_fn=<MseLossBackward0>)
tensor(0.0479, grad_fn=<MseLossBackward0>)
tensor(0.0476, grad_fn=<MseLossBackward0>)
tensor(0.0473, grad_fn=<MseLossBackward0>)
tensor(0.0470, grad_fn=<MseLossBackward0>)
tensor(0.0468, grad_fn=<MseLossBackward0>)
tensor(0.0465, grad_fn=<MseLossBackward0>)
tensor(0.0462, grad_fn=<MseLossBackward0>)
tensor(0.0459, grad_fn=<MseLossBackward0>)
tensor(0.0456, grad_fn=<MseLossBackward0>)
tensor(0.0454, grad_fn=<MseLossBackward0>)
tensor(0.0451, grad_fn=<MseLossBackward0>)
tensor(0.0448, grad_fn=<MseLossBackward0>)
tensor(0.0446, grad_fn=<MseLossBackward0>)
tensor(0.0443, grad_fn=<MseLossBackward0>)
tensor(0.0440, grad_fn=<MseLossBackward0>)
tensor(0.0438, grad_fn=<MseLossBackward0>)
tensor(0.0435, grad_fn=<MseLossBackward0>)
tensor(0.0432, grad_fn=<MseLossBackward0>)
tensor(0.0430, grad_fn=<MseLossBackward0>)
tensor(0.0427, grad_fn=<MseLossBackward0>)
tensor(0.0425, grad_fn=<MseLossBackward0>)
tensor(0.0422, grad_fn=<MseLossBackward0>)
tensor(0.0420, grad_fn=<MseLossBackward0>)
tensor(0.0417, grad_fn=<MseLossBackward0>)
tensor(0.0415, grad_fn=<MseLossBackward0>)
tensor(0.0412, grad_fn=<MseLossBackward0>)
- 数据集准备 x_train, y_train
- 训练迭代
- 梯度清零 optimize.zero_grad()
- 前向传播
- 计算损失
- 反向传播
- 更新参数
相关文章:
)
小白入门pytorch(一)
本文为小白入门Pytorch中的学习记录博客 小白入门pytorch 基础知识 导入torch,查看torch版本 import torch print(torch.__version__)输出结果: 1.12.1cu113张量 在pytorch中,张量(tensor)是最基本的数据结构。 …...

【STM32笔记】HAL库I2C通信配置、读写操作及通用函数定义
【STM32笔记】HAL库I2C通信配置、读写操作及通用函数定义 文章目录 I2C协议I2C配置I2C操作判断I2C是否响应I2C读写 附录:Cortex-M架构的SysTick系统定时器精准延时和MCU位带操作SysTick系统定时器精准延时延时函数阻塞延时非阻塞延时 位带操作位带代码位带宏定义总…...
Direct3D模板缓存
模板缓存是一个用于获得某种特效的离屏缓存,模板缓存的分辨率与后台缓存和深度缓存的分辨率完全相同,所以像素也是一一对应的,模板缓存允许我们动态的,有针对性的决定是否将某个像素写入后台缓存中。 例如实现镜面效果时…...

在windows上执行ssh-keygen报错Bad permissions
在windows上执行ssh-keygen报错Bad permissions:如下 C:\Users\xiaoming>ssh-keygen -p -m PEM -f C:\mywork\id_rsa Bad permissions. Try removing permissions for user: BUILTIN\\Users (S-1-6-92-143) on file C:/mywork/id_rsa.WARNING: UNPROTECTED PRIV…...
给Proxmox VE 虚拟机分配巨大分区惹麻烦
由于缺乏良好的规划,有开发人员直接在公有云采购一个容量超过100TB的NAS存储,使用过程中,数据的存储也没有规划,业务数据一股脑的写入到同一个目录,下边的子目录没有规律,用用户的图片、视频、访问日志、甚…...
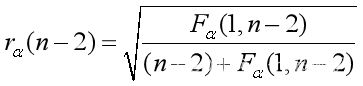
数学建模——统计回归模型
一、基本知识 1、基本统计量 总体:研究对象的某个感兴趣的指标。样本:从总体中随机抽取的独立个体X1,X2,…,Xn,一般称(X1,…,Xn)为一个样本,可以看成一个n维随机向量,它的每一取组值(x1,…,xn)称为样本的观测值。统计…...

C++【个人笔记1】
1.C的初识 1.1 简单入门 #include<iostream> using namespace std; int main() {cout << "hello world" << endl;return 0; } #include<iostream>; 预编译指令,引入头文件iostream.using namespace std; 使用标准命名空间cout …...

博通强迫三星签不平等长约,被韩处罚1亿元 | 百能云芯
近日,博通(Broadcom)这家国际知名的半导体公司因其市场主导地位的滥用,遭到了韩国公平贸易委员会(FTC)的严厉制裁,罚款高达191亿韩元,约合人民币1.04亿元。这一惩罚背后的故事揭示了…...
版本控制 Sourcetree
Sourcetree软件做版本控制,小程序的代码和springboot项目的代码放到同一个文件夹下, 无脑安装就行 命名就用项目名bkd表示springboot项目名 项目命名xcx表示小程序 每次上传代码,一定要先拉下代码不然代码冲突处理起来比较麻烦...

题目 1059: 二级C语言-等差数列
题目描述 sum2581114…,输入正整数n,求sum的前n项和。样例输入 2样例输出 7 根据题目我们得知,求一个等差数列的和。 等差数列的下一项前一项d。d是等差。 根据这个直接求每一项,再加进sum的和,最后输出即可。 在本题中…...

HarmonyOS 如何使用异步并发能力进行开发
一、并发概述 并发是指在同一时间段内,能够处理多个任务的能力。为了提升应用的响应速度与帧率,以及防止耗时任务对主线程的干扰,HarmonyOS 系统提供了异步并发和多线程并发两种处理策略。 ● 异步并发是指异步代码在执行到一定程度后会被暂…...

时间格式化时候HH和hh的区别
SimpleDateFormat simpleDateFormatnew SimpleDateFormat("yyyy-MM-dd HH:mm:ss"); simpleDateFormat.format(new Date()) HH(大写):表示使用24小时制(也称为军用时间制)来表示小时。它的范围是从00到23。例…...

aliyunoss上传图片
依赖 <dependency><groupId>com.aliyun.oss</groupId><artifactId>aliyun-sdk-oss</artifactId><version>3.8.1</version></dependency>配置文件 config:alioss:endpoint: oss-cn-shanghai.aliyuncs.com(节点名 我…...

动手吧,vue数字动画
数字动画,有数字的地方都能用上,拿去吧! 效果: 1、template部分 <template><div class"v-count-up">{{ dispVlaue }}</div> </template> 2、js部分 export default {data() {return {timer…...

Android12之仿Codec2.0实现传递编解码器组件本质(四十六)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生从来没有捷径,只有行动才是治疗恐惧和懒惰的唯一良药. 更多原创,欢迎关注:Android…...

MongoDB【部署 04】Windows系统实现MongoDB多磁盘存储
Windows系统实现多磁盘存储 1.为什么2.多磁盘存储2.1 数据库配置2.2 文件夹磁盘映射2.3 创建新的数据集 3.总结 1.为什么 这里仅针对只有一台Windows系统服务器的情景: 当服务器存储不足时,或者要接入更多的数据,就会挂载新磁盘,…...

ruoyi框架使用自定义用户表登录
背景 有的时候我们做框架升级或改造的时候,需要用到原来的部分表,比如只是用ruoyi的框架,然后登录的用户逻辑还是想用自己的表,那么接下来这边文章将介绍修改逻辑。 修改教程 1、SysLoginController.java 大家找到这个login方…...

计算机视觉与深度学习-卷积神经网络-卷积图像去噪边缘提取-卷积-[北邮鲁鹏]
目录标题 参考学习链接卷积的定义卷积的性质叠加性平移不变性交换律结合律分配律标量 边界填充边界填充方法 - 常数填充最常用常数填充零填充(zero padding)拉伸镜像 卷积示例单位脉冲核无变化平移平滑锐化 卷积核平均卷积核高斯卷积核高斯卷积核定义高斯…...

JS手动实现发布者-订阅者模式
发布-订阅模式是一种对象间一对多的依赖关系,当一个对象的状态发送改变时,所有依赖于它的对象都将得到状态改变的通知。具体过程是:订阅者把自己想订阅的事件注册到调度中心,当发布者更新该事件时通知调度中心,由调度中…...

【含面试题】MySQL死锁日志分析与解决的Java代码实现
AI绘画关于SD,MJ,GPT,SDXL百科全书 面试题分享点我直达 2023Python面试题 2023最新面试合集链接 2023大厂面试题PDF 面试题PDF版本 java、python面试题 项目实战:AI文本 OCR识别最佳实践 AI Gamma一键生成PPT工具直达链接 玩转cloud Studio 在线编码神器 玩转 GPU AI…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...
