经管博士科研基础【25】概率论中的相关基础概念
1. Support
在概率论中,"support"(支撑集)是指随机变量可能取值的集合。对于离散型随机变量,支撑集包含了所有可能的取值;而对于连续型随机变量,支撑集是指其密度函数或概率质量函数非零的区域。
举个例子来说,对于一个离散型随机变量,比如抛硬币的结果(正面或反面),其支撑集就是{正面, 反面},因为这两个是唯一可能的结果。
对于一个连续型随机变量,比如服从标准正态分布的随机变量,其支撑集是整个实数轴,因为概率密度函数在整个实数轴上都有定义并且非零。
支撑集的概念在概率论中很重要,因为它决定了随机变量的取值范围和可能性。
2. hazard rate function
在概率论中,"hazard rate"(风险率)是指在给定时间点上事件发生的条件下,该事件在下一个时间间隔内发生的概率密度。风险率常被用于描述随机事件的失效或故障概率随时间的变化情况。
对于一个随机事件,其风险率函数可以表示为 h(t),其中 t 表示时间。风险率函数可以告诉我们在特定时间点上,事件失败的速率或概率密度。
具体来说,对于一个连续型随机变量 X,其风险率函数可以定义为:
h(t) = f(t) / S(t)
其中,f(t) 是事件在时间点 t 失效的概率密度函数,S(t) 是累积分布函数。
风险率在可靠性工程和生存分析中非常有用,能够帮助研究者估计和分析随机事件发生的概率和时间相关性。通过分析风险率,人们可以评估事件的可靠性、寿命分布以及预测未来的风险情况。
相关文章:

经管博士科研基础【25】概率论中的相关基础概念
1. Support 在概率论中,"support"(支撑集)是指随机变量可能取值的集合。对于离散型随机变量,支撑集包含了所有可能的取值;而对于连续型随机变量,支撑集是指其密度函数或概率质量函数非零的区域。…...
)
计算机网络的相关知识点总结(一)
1.谈一谈对OSI七层模型和TCP/IP四层模型的理解? 不管是OSI七层模型亦或是TCP/IP四层模型,它们的提出都有一个共同的目的:通过分层来将复杂问题细化,通过各个层级之间的相互配合来更好的解决计算机中出现的问题。 说到分层…...
下载github.com上的依赖资源
下载github.com上的依赖资源(需要反复试才能成功,所以单独安装) export GIT_TRACE1 export GIT_CURL_VERBOSE1 pip install githttps://github.com/PanQiWei/AutoGPTQ.git -i https://pypi.mirrors.ustc.edu.cn/simple --trusted-hostpypi.mi…...

编写 GPT 提示词的公式 + 资源分享
GPT 能够给我们带来很大的帮助,因此我们要好好利用它。我们希望 GPT 输出令我们满意的内容,影响 GPT 输出内容的因素有模型和输入(Prompt,提示词)。 模型:我们可以选择不同的 GPT 产品,它们的模…...
用HTML、CSS和JavaScript制作的通用进制转换器
随着编程和计算机科学越来越受欢迎,我们经常需要进行进制转换。本文将介绍一个简洁、美观、适用于移动设备的进制转换工具,并详细讨论其实现。 目录 🌍 用HTML、CSS和JavaScript制作的通用进制转换器 1.项目图片展示 2. 技术栈 3. 主要功…...
ArcGIS 10.3软件安装包下载及安装教程!
【软件名称】:ArcGIS 10.3 【安装环境】:Windows 【下载链接 】: 链接:https://pan.baidu.com/s/1K5ab7IHMYa23HpmuPkFa1A 提取码:oxbb 复制这段内容后打开百度网盘手机App,操作更方便哦 软件解压码点击原文…...

【数据增强】
【数据增强】 1 数据增强的情形2 数据增强的方法 1 数据增强的情形 当数据比较小,难以获取新的训练数据时,可以考虑数据增强,如随机裁剪部分,随机左右上下翻转、随机旋转一个角度、随机亮度变化等微小变化,数据的多样…...

Ae 效果:CC Force Motion Blur
时间/CC Force Motion Blur Time/CC Force Motion Blur CC Force Motion Blur (CC 强制运动模糊)主要用于为动态图像添加强制的运动模糊效果,增加动态画面的流畅感和真实感。 相对于时间轴面板上的“运动模糊”开关,CC Force Moti…...

2023华为杯研究生数学建模竞赛CDEF题思路+模型代码
全程更新华为杯研赛CDEF题思路模型及代码,大家查看文末名片获取 华为杯C题思路分析 问题一 在每个评审阶段,作品通常都是随机分发的,每份作品需要多位评委独立评审。为了增加不同评审专家所给成绩之间的可比性,不同专家评审的作…...

FP独立站之黑科技:AB站收款、斗篷CLOAK
最近一段时间经常有不少小伙伴来咨询我独立站的相关的业务,因为很多独立站卖家觉得独立站不好做,再加上跨境平台禁止特货类产品的销售(如FP产品、成人用品、电子烟、灰黑类产品等等),但这类产品市场需求大,…...
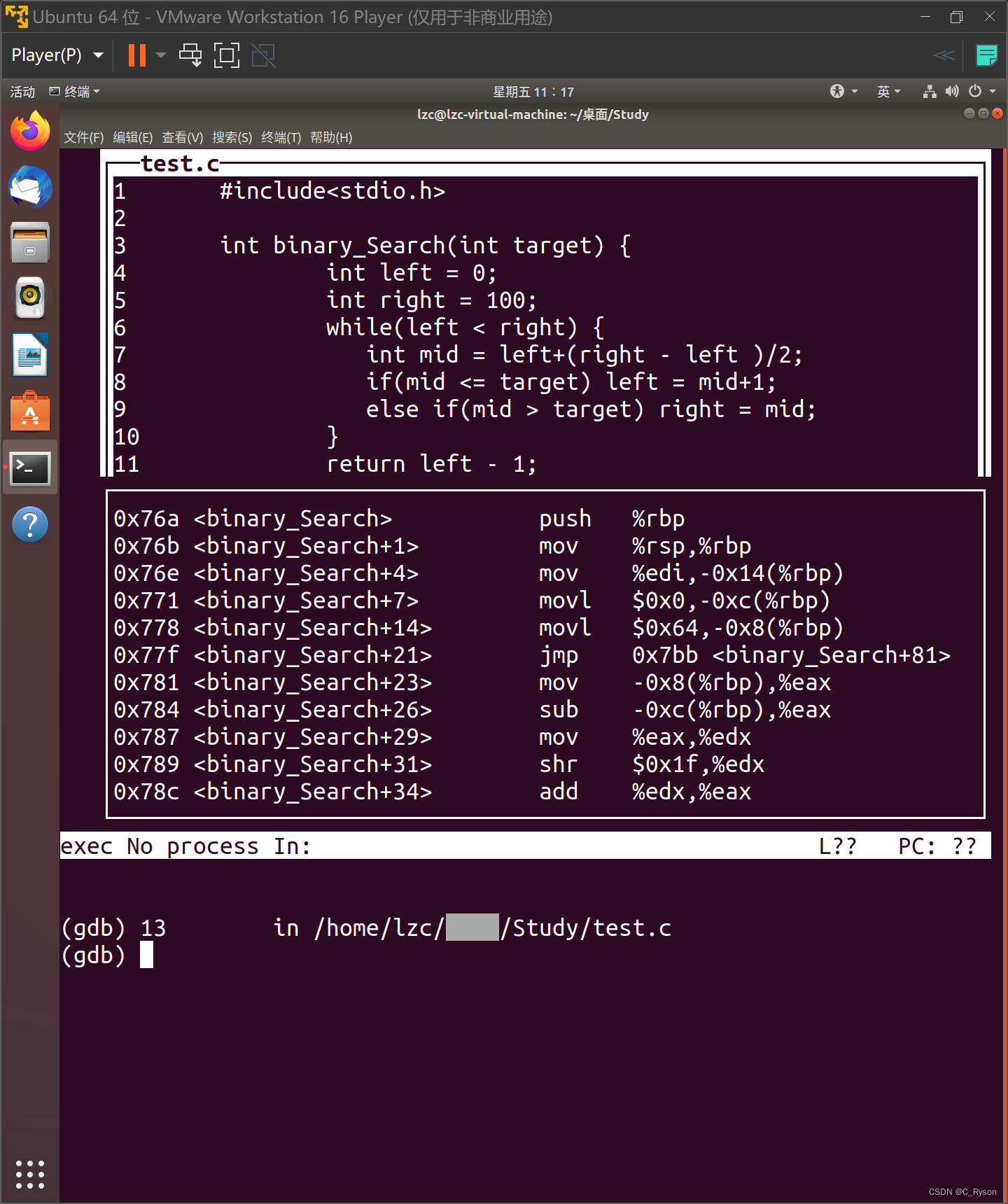
【Linux网络编程】gdb调试技巧
这篇博客主要要记录一下自己在Linux操作系统Ubuntu下使用gbd调试程序的一些指令,以及使用过程中的一些心得。 使用方法 可以使用如下代码 gcc -g test.c -o test 或者 gcc test.c -o test -g的选项最好添加,如果不添加,l指令无法被识别 …...
ElementUI之登录与注册
目录 一.前言 二.ElementUI的简介 三.登录注册前端界面的开发 三.vue axios前后端交互--- Get请求 四.vue axios前后端交互--- Post请求 五.跨域问题 一.前言 这一篇的知识点在前面两篇的博客中就已经详细详解啦,包括如何环境搭建和如何建一个spa项目等等知识…...

报错处理:Error: Redis server is running but Redis CLI cannot connect
嗨,读者朋友们!今天我来跟大家分享一个我在运维过程中遇到的一个关于Linux上运行Redis服务时的报错及解决方法。 报错信息如下: Error: Redis server is running but Redis CLI cannot connect 这个报错信息表明Redis服务器已经运行ÿ…...

RocketMQ 源码分析——Producer
文章目录 消息发送代码实现消息发送者启动流程检查配置获得MQ客户端实例启动实例定时任务 Producer 消息发送流程选择队列默认选择队列策略故障延迟机制策略*两种策略的选择 技术亮点:ThreadLocal 消息发送代码实现 下面是一个生产者发送消息的demo(同步发送&#…...

ISTQB术语表
此术语表为国际软件测试认证委员会(ISTQB)发布的标准术语表。此表历经数次修改、完善,集纳了计算机行业界、商业界及政府相关机构的见解及意见,在国际化的层面上达到了罕有的统一性及一致性。参与编制此表的国际团体包括澳大利亚、…...
小米笔试题——01背包问题变种
这段代码的主要思路是使用动态规划来构建一个二维数组 dp,其中 dp[i][j] 表示前 i 个产品是否可以组合出金额 j。通过遍历产品列表和可能的目标金额,不断更新 dp 数组中的值,最终返回 dp[N][M] 来判断是否可以组合出目标金额 M。如果 dp[N][M…...

SkyWalking内置MQE语法
此文档出自SkyWalking官方git https://github.com/apache/skywalking docs/en/api/metrics-query-expression.md Metrics Query Expression(MQE) Syntax MQE is a string that consists of one or more expressions. Each expression could be a combination of one or more …...
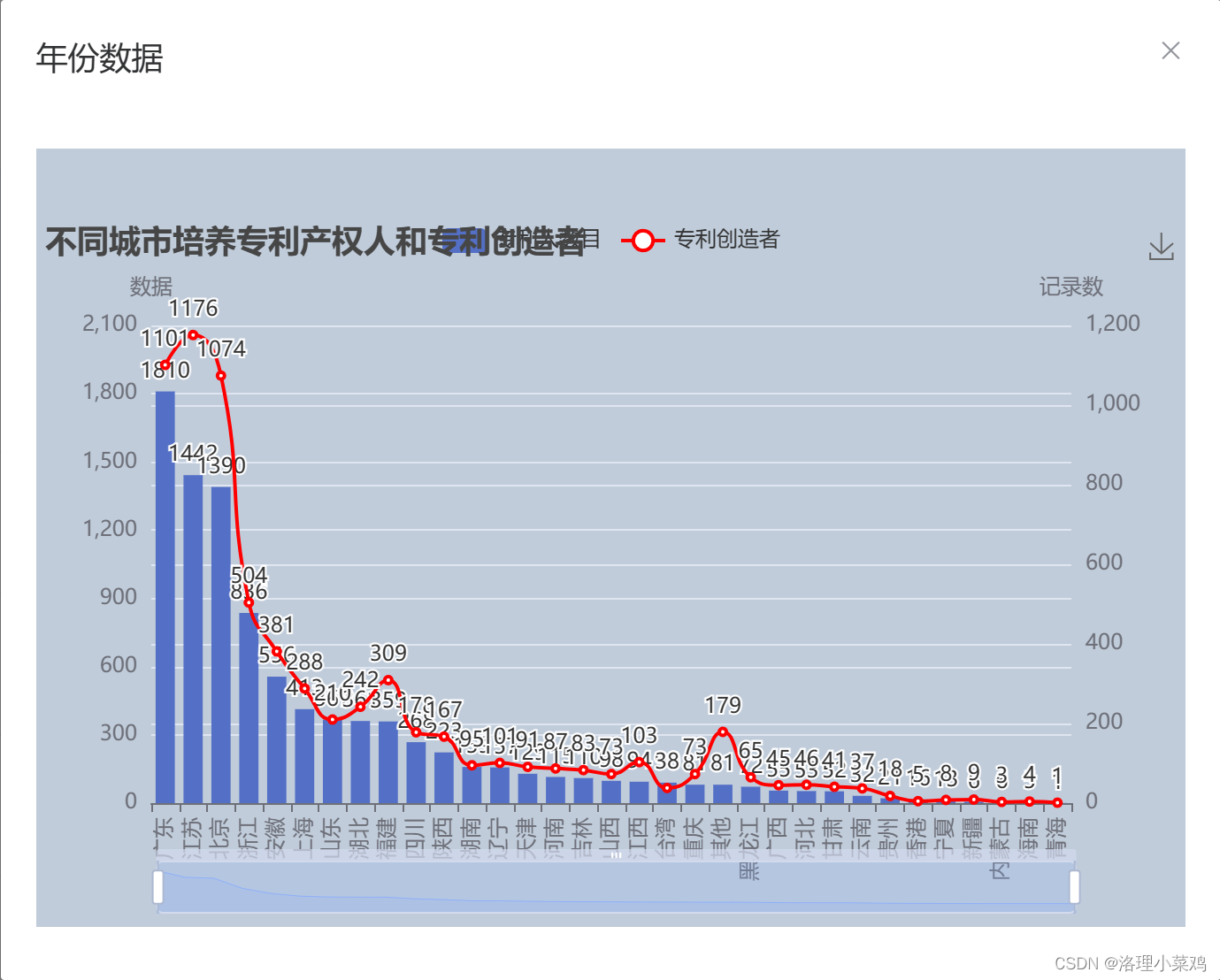
Springboot2 Pandas Pyecharts 量子科技专利课程设计大作业
数据集介绍 1.背景 根据《中国科学:信息科学》期刊上的一篇文章,量子通信包括多种协议与应用类型: 基于量子隐形传态与量子存储中继等技术,可实现量子态信息传输,进而构建量子信息网络,已成为当前科研热点&…...

RabbitMQ里的几个重要概念
RabbitMQ中的一些角色: publisher:生产者consumer:消费者exchange个:交换机,负责消息路由,接受生产者发送的消息,把消息发送到一个或多个队列里queue:队列,存储消息virt…...

23. 图论 - 图的由来和构成
文章目录 图的由来图的构成Hi, 你好。我是茶桁。 从第一节课上到现在,我基本上把和人工智能相关的一些数学知识都教给大家了,终于来到我们人工智能数学的最后一个部分了,让我们从今天开始进入「图论」。 图论其实是一个比较有趣的领域,因为微积分其实更多的是对应连续型的…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
