李航老师《统计学习方法》第2章阅读笔记
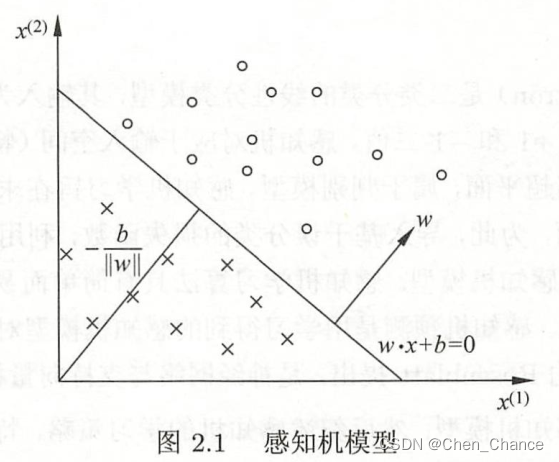
感知机(perceptron)时二类分类的线性分类模型,其输入为实例的特征向量,输出为实例的类别,取+1和-1二值。感知机对应于输入空间(特征空间)中将实例划分为正负两类的分离超平面
想象一下在一个平面上有一些红点和蓝点,这些点代表不同的类别。分离超平面就是一条线,可以将红点和蓝点分开,使得所有的红点都在一侧,而蓝点都在另一侧。这条线(或者平面,对于高维数据)被称为分离超平面。
2.1感知机模型
定义2.1(感知机):假设输入空间(特征空间)是 X ⊆ R n X \subseteq R^n X⊆Rn,输出空间是 Y = { + 1 , − 1 } Y=\{+1,-1\} Y={+1,−1}。输入 x ∈ X x \in X x∈X表示实例的特征向量,对应于输入空间(特征空间)的点;输出 y ∈ Y y \in Y y∈Y表示实例的类别。由输入空间到输出空间的如下函数:
f ( x ) = s i g n ( w ⋅ x + b ) f(x)=sign(w \cdot x+b) f(x)=sign(w⋅x+b)
称为感知机。其中,w和b为感知机模型参数, w ∈ R n w \in R^n w∈Rn叫做权重(weight)或权重向量(weight vector), b ∈ R b \in R b∈R叫做偏置(bias), w ⋅ x w \cdot x w⋅x表示w和x的内积。sign是符号函数,即
s i g n ( x ) = { + 1 x ≥ 0 − 1 x < 0 sign(x)=\begin{cases} +1 & x≥0 \\ -1 & x<0 \\ \end{cases} sign(x)={+1−1x≥0x<0
内积是线性代数中的一个概念,也被称为点积或标量积。它是两个向量之间的一种运算,将两个向量相乘并得到一个标量(实数)的结果。内积通常用于衡量向量之间的相似性、角度和投影等性质。
内积的一般定义是:
对于两个实数向量 a 和 b,它们的内积(点积)表示为 a·b,计算方式如下:
a·b = |a| * |b| * cos(θ)
以下是一个简单的例子来说明内积的概念:
假设有两个二维向量 a 和 b,它们分别表示为:
a = [2, 3]
b = [4, 1]
要计算 a 和 b 的内积,首先需要计算它们的长度(模):
|a| = √(2^2 + 3^2) = √(4 + 9) = √13
|b| = √(4^2 + 1^2) = √(16 + 1) = √17
接下来,计算 a 和 b 之间的夹角 θ,可以使用余弦公式:
cos(θ) = (a·b) / (|a| * |b|)
将 a 和 b 的值代入:
cos(θ) = (2 * 4 + 3 * 1) / (√13 * √17) = (8 + 3) / (√13 * √17) = 11 / (√13 * √17)
现在,我们可以计算内积 a·b:
a·b = |a| * |b| * cos(θ) = √13 * √17 * (11 / (√13 * √17)) = 11
所以,向量 a 和 b 的内积是 11。
内积的计算可以帮助我们理解向量之间的相对方向以及它们之间的相似性。在许多应用中,内积是一个重要的数学工具,例如在机器学习中用于计算特征之间的相关性,以及在物理学中用于计算力学和电磁学中的各种问题。
感知机模型的参数包括权重(weight)向量 w ∈ R n w \in \mathbb{R}^n w∈Rn 和偏置(bias) b ∈ R b \in \mathbb{R} b∈R,这两个参数的维度之所以不同,是因为它们的作用和数学表达的需要不同。
- 权重向量 w ∈ R n w \in \mathbb{R}^n w∈Rn:
- 权重向量 w w w 的维度为 n n n,其中 n n n 表示输入特征的数量。每个特征都有一个对应的权重,用于衡量该特征对模型的重要性。权重向量中的每个元素 w i w_i wi 对应于一个特征,表示该特征在模型中的权重。每个特征都有一个权重,因此需要 n n n 个权重值。
- 偏置 b ∈ R b \in \mathbb{R} b∈R:
- 偏置 b b b 是一个标量(单个实数),它不依赖于特征的数量。偏置的作用是在计算模型的输出时引入一个偏移量,用于调整模型的预测值。它可以理解为模型在没有任何特征输入时的输出值,相当于截距或偏移项。
考虑一个简单的情况,比如二元分类问题,输入特征有 n n n 个,感知机模型的输出是根据权重向量 w w w 对输入特征加权求和后再加上偏置 b b b,然后通过 sign 函数进行分类决策。这就是为什么需要一个长度为 n n n 的权重向量 w w w 和一个标量偏置 b b b 的原因。
总之,权重向量 w w w 的维度与输入特征的数量相关,而偏置 b b b 是一个标量,不依赖于特征的数量,它们一起组成了感知机模型的参数,用于对输入进行线性加权和分类决策。
2.2感知机学习策略
2.2.1数据集的线性可分性
定义2.2(数据集的线性可分性)
2.2.2感知机学习策略
2.3感知机学习算法
2.3.1感知机学习算法的原始形式
∇ w L ( w , b ) = − ∑ x i ∈ M y i x i \nabla_wL(w,b)=-\sum\limits_{x_i \in M}y_i x_i ∇wL(w,b)=−xi∈M∑yixi
∇ b L ( w , b ) = − ∑ x i ∈ M y i \nabla_bL(w,b)=-\sum\limits_{x_i \in M}y_i ∇bL(w,b)=−xi∈M∑yi
这两个公式是关于损失函数 L ( w , b ) L(w, b) L(w,b) 对于模型参数 w w w 和 b b b 的梯度计算。
- ∇ w L ( w , b ) = − ∑ x i ∈ M y i x i \nabla_wL(w,b)=-\sum\limits_{x_i \in M}y_i x_i ∇wL(w,b)=−xi∈M∑yixi 表示损失函数 L ( w , b ) L(w, b) L(w,b) 对于权重参数 w w w 的梯度。具体来说,它告诉我们如何调整权重 w w w 才能最小化损失函数。右侧的求和项计算了关于样本 x i x_i xi 的损失函数的梯度,然后取负号表示梯度下降。这个梯度向量告诉我们,在参数 w w w 的当前值下,每个样本 x i x_i xi 对于损失函数的贡献如何,以及如何将权重 w w w 调整以降低损失。
- ∇ b L ( w , b ) = − ∑ x i ∈ M y i \nabla_bL(w,b)=-\sum\limits_{x_i \in M}y_i ∇bL(w,b)=−xi∈M∑yi 表示损失函数 L ( w , b ) L(w, b) L(w,b) 对于偏置参数 b b b 的梯度。类似地,它告诉我们如何调整偏置 b b b 才能最小化损失函数。右侧的求和项计算了所有样本 x i x_i xi 的标签 y i y_i yi 的总和,然后取负号表示梯度下降。这个梯度值告诉我们,在参数 b b b 的当前值下,所有样本的标签对于损失函数的贡献如何,以及如何将偏置 b b b 调整以降低损失。
这两个梯度计算是优化算法(如梯度下降)中的关键步骤,用于更新模型的参数 w w w 和 b b b 以最小化损失函数。通过迭代地计算这些梯度并更新参数,我们可以让模型逐渐收敛到一个使损失最小化的参数组合,从而提高模型的性能。
算法2.1(感知机学习算法的原始形式)

2.3.2算法的收敛性
我们现在证明了,对于线性可分数据集感知机学习算法原始形式收敛(即经过有限次迭代可以得到一个将训练数据集完全正确划分的分离超平面及感知机模型)

定理2.1(Novikoff)设训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\} T={(x1,y1),(x2,y2),...,(xN,yN)}是线性可分的,其中 x i ∈ X = R n , y i ∈ Y = { − 1 , + 1 } , I = 1 , 2 , . . . , N x_i \in X=R^n,y_i \in Y=\{-1,+1\},I=1,2,...,N xi∈X=Rn,yi∈Y={−1,+1},I=1,2,...,N,则
(1)存在满足条件 ∣ ∣ w ^ o p t ∣ ∣ = 1 ||\hat w _{opt}||=1 ∣∣w^opt∣∣=1的超平面 w ^ o p t ⋅ x ^ = w o p t ⋅ x + b o p t = 0 \hat w _{opt}\cdot \hat x=w_{opt}\cdot x+b_{opt}=0 w^opt⋅x^=wopt⋅x+bopt=0将训练数据集完全正确分开;且存在 γ > 0 \gamma>0 γ>0,对所有 i = 1 , 2 , . . . , N i=1,2,...,N i=1,2,...,N
y i ( w ^ o p t ⋅ x ^ ) = y i ( w o p t ⋅ x + b o p t ) ≥ γ y_i(\hat w _{opt}\cdot \hat x)=y_i( w _{opt}\cdot x+b_{opt})≥\gamma yi(w^opt⋅x^)=yi(wopt⋅x+bopt)≥γ
(2)令 R = max 1 ≤ i ≤ N ∣ ∣ x ^ i ∣ ∣ R=\max \limits_{1≤i≤N}||\hat x_i|| R=1≤i≤Nmax∣∣x^i∣∣,则感知机算法2.1在训练数据集上的误分类次数k满足不等式
k ≤ ( R γ ) 2 k≤(\frac{R}{\gamma})^2 k≤(γR)2
这是关于 Novikoff 收敛定理的详细数学描述和解释:
定理背景:
- 给定一个训练数据集 T T T,其中包含 N N N 个样本,每个样本的特征是 x i ∈ R n x_i \in \mathbb{R}^n xi∈Rn,标签是 y i ∈ { − 1 , + 1 } y_i \in \{-1, +1\} yi∈{−1,+1}。这个数据集被假定为线性可分,意味着存在一个超平面 w ^ o p t ⋅ x ^ = 0 \hat w_{opt} \cdot \hat x = 0 w^opt⋅x^=0 可以完全正确地将所有样本分开,其中 w ^ o p t \hat w_{opt} w^opt 是法向量,满足 ∣ ∣ w ^ o p t ∣ ∣ = 1 ||\hat w_{opt}|| = 1 ∣∣w^opt∣∣=1, w o p t w_{opt} wopt 是权重向量, b o p t b_{opt} bopt 是偏置项。
- 定理要证明的是,对于这个线性可分的数据集,感知机算法在训练数据集上的误分类次数 k k k 受到一定的上界限制。
定理内容解释:
- (1)部分:该部分说明了存在一个超平面 w ^ o p t ⋅ x ^ = 0 \hat w_{opt} \cdot \hat x = 0 w^opt⋅x^=0 可以完全正确地分开训练数据集,并且存在一个正数 γ > 0 \gamma > 0 γ>0,使得对于所有训练样本 ( x i , y i ) (x_i, y_i) (xi,yi),都有 y i ( w ^ o p t ⋅ x ^ ) ≥ γ y_i(\hat w_{opt} \cdot \hat x) \geq \gamma yi(w^opt⋅x^)≥γ。这意味着超平面 w ^ o p t ⋅ x ^ = 0 \hat w_{opt} \cdot \hat x = 0 w^opt⋅x^=0 在每个样本点上的分类间隔都至少为 γ \gamma γ。
- (2)部分:该部分说明了感知机算法在训练数据集上的误分类次数 k k k 有一个上界。具体来说,误分类次数 k k k 满足不等式 k ≤ ( R γ ) 2 k \leq \left(\frac{R}{\gamma}\right)^2 k≤(γR)2,其中 R R R 是训练数据集中样本特征的最大范数(绝对值的最大值), γ \gamma γ 是前面提到的正数。这个不等式表明,误分类次数 k k k 受到了数据集的特征范数和分类间隔 γ \gamma γ 的限制,误分类次数不能超过这个上界。
解释:
- 定理的第一部分告诉我们,对于线性可分的数据集,存在一个合适的超平面,可以将所有样本正确分类,并且这个超平面在每个样本点上都有足够大的分类间隔 γ \gamma γ。这个分类间隔 γ \gamma γ 可以看作是超平面离每个样本点的距离,越大表示分类得越确信。
- 定理的第二部分告诉我们,感知机算法在训练数据集上的误分类次数是有界的,上界由数据集中的特征范数 R R R 和分类间隔 γ \gamma γ 决定。这意味着无论感知机算法如何迭代更新权重,它最终将停止,不会永远继续分类错误。误分类次数的上限是关于数据集和分类间隔的一个函数,当 R R R 和 γ \gamma γ 较小时,误分类次数上限也较小,表明算法更容易收敛。
这个定理强调了感知机算法在线性可分数据上的性质,为我们提供了关于算法收敛性和分类性能的理论保证。
w ^ o p t \hat w_{opt} w^opt 和 w o p t w_{opt} wopt 是两个不同的符号,它们用于表示定理中的两个不同的向量:
- w ^ o p t \hat w_{opt} w^opt:这个符号表示的是一个单位向量,通常用来表示一个超平面的法向量。在定理中, w ^ o p t \hat w_{opt} w^opt 表示一个单位法向量,它是一个指向超平面的方向,并用于将数据集分开。单位向量的长度(范数)等于 1。
- w o p t w_{opt} wopt:这个符号表示的是一个权重向量,通常用于线性分类器或超平面模型。在定理中, w o p t w_{opt} wopt 是一个用于定义超平面的向量,它包括了每个特征的权重。与 w ^ o p t \hat w_{opt} w^opt 不同, w o p t w_{opt} wopt 不一定是单位向量,它的长度可以不为 1。
总之, w ^ o p t \hat w_{opt} w^opt 和 w o p t w_{opt} wopt 在定理中表示了两个不同的向量,前者通常是一个单位法向量,后者是一个权重向量,它们在超平面模型中具有不同的作用和含义。
x ^ \hat x x^ 和 x x x 通常表示不同的概念:
- x x x:这是一个通常表示数据点或样本的符号,它包含样本的特征值。在机器学习和统计中,通常将一个数据点或样本表示为一个特征向量 x x x,其中包含了该样本的各个特征的数值。例如,如果我们在分类问题中考虑一个图像, x x x 可以表示该图像的各个像素值或特征提取后的特征值。 x x x 是数据集中的每个样本的不同实例。
- x ^ \hat x x^:这个符号通常用于表示一个单位向量或规范化向量。在一些数学和机器学习上下文中, x ^ \hat x x^ 可以表示将向量 x x x 标准化为单位长度的向量,也就是将其长度(范数)归一化为1。这种标准化常用于定义方向或表示规范化特征。例如,如果 x x x 是一个普通的特征向量, x ^ \hat x x^ 可以表示与 x x x 具有相同方向但长度为1的向量。
总的来说, x x x 通常表示原始数据或特征向量,而 x ^ \hat x x^ 表示具有单位长度的向量或规范化向量。根据上下文,它们可以具有不同的含义和用途。
∣ ∣ x ^ i ∣ ∣ ||\hat x_i|| ∣∣x^i∣∣ 表示向量 x ^ i \hat x_i x^i 的范数(或长度)。范数是一个数学概念,它用于衡量向量在空间中的大小或长度。
在这个上下文中, x ^ i \hat x_i x^i 通常表示一个向量,例如一个特征向量。 ∣ ∣ x ^ i ∣ ∣ ||\hat x_i|| ∣∣x^i∣∣ 就是该向量的范数,它可以有不同的定义方式,包括:
- L2范数(欧几里德范数): ∣ ∣ x ^ i ∣ ∣ 2 ||\hat x_i||_2 ∣∣x^i∣∣2 表示向量 x ^ i \hat x_i x^i 的L2范数,定义为向量各个元素的平方和的平方根。即 ∣ ∣ x ^ i ∣ ∣ 2 = ∑ j = 1 n ( x ^ i [ j ] ) 2 ||\hat x_i||_2 = \sqrt{\sum_{j=1}^{n} (\hat x_i[j])^2} ∣∣x^i∣∣2=∑j=1n(x^i[j])2,其中 n n n 是向量的维度。L2范数衡量了向量的长度。
- L1范数(曼哈顿范数): ∣ ∣ x ^ i ∣ ∣ 1 ||\hat x_i||_1 ∣∣x^i∣∣1 表示向量 x ^ i \hat x_i x^i 的L1范数,定义为向量各个元素的绝对值之和。即 ∣ ∣ x ^ i ∣ ∣ 1 = ∑ j = 1 n ∣ x ^ i [ j ] ∣ ||\hat x_i||_1 = \sum_{j=1}^{n} |\hat x_i[j]| ∣∣x^i∣∣1=∑j=1n∣x^i[j]∣。L1范数衡量了向量各个元素的绝对值之和。
- 无穷范数: ∣ ∣ x ^ i ∣ ∣ ∞ ||\hat x_i||_{\infty} ∣∣x^i∣∣∞ 表示向量 x ^ i \hat x_i x^i 的无穷范数,定义为向量中绝对值最大的元素。即 ∣ ∣ x ^ i ∣ ∣ ∞ = max j ∣ x ^ i [ j ] ∣ ||\hat x_i||_{\infty} = \max_{j} |\hat x_i[j]| ∣∣x^i∣∣∞=maxj∣x^i[j]∣。
不同的范数衡量了向量的不同性质,例如长度、绝对值之和、最大绝对值等。具体使用哪种范数取决于问题的性质和需求。
2.3.3感知机学习算法的对偶形式

相关文章:

李航老师《统计学习方法》第2章阅读笔记
感知机(perceptron)时二类分类的线性分类模型,其输入为实例的特征向量,输出为实例的类别,取1和-1二值。感知机对应于输入空间(特征空间)中将实例划分为正负两类的分离超平面 想象一下在一个平面…...
ruoyi框架修改左侧菜单样式
菜单效果 ruoyi前端框架左侧的菜单很丑,我们需要修改一下样式,下面直接看效果。 修改代码 1、sidebar.scss .el-menu-item, .el-submenu__title {overflow: hidden !important;text-overflow: ellipsis !important;white-space: nowrap !important;//…...

【已解决】PyCharm里的黄色波浪线
问题描述 有时候在PyCharm中某些代码下面会有黄色波浪线。 问题解释 黄色波浪线只是提示这段代码不规范,但对程序的运行并没有本质影响。...
)
设计模式:策略模式(C++实现)
策略模式(Strategy Pattern)是一种行为设计模式,它定义了一系列的算法,并将每个算法封装成独立的对象,使得它们可以互相替换。下面是一个使用C实现策略模式的示例: #include <iostream>// 抽象策略类…...

网络安全深入学习第二课——热门框架漏洞(RCE—Thinkphp5.0.23 代码执行)
文章目录 一、什么是框架?二、导致框架漏洞原因二、使用步骤三、ThinkPHP介绍四、Thinkphp框架特征五、Thinkphp5.0.23 远程代码执行1、漏洞影响范围2、漏洞成因 六、POC数据包Windows下的Linux下的 七、漏洞手工复现1、先Burp抓包,把抓到的请求包发送到…...

Pdf文件签名检查
如何检查pdf的签名 首先这里有一个已经签名的pdf文件,通过pdf软件可以看到文件的数字签名。 图1为签名后的文件,图2为签名后文件被篡改。 下面就是如何代码检查这里pdf文件的签名 1.引入依赖 <dependency><groupId>org.projectlombok<…...

web前端之float布局与flex布局
float布局 <style>.nav {overflow: hidden;background-color: #6adfd0; /* 导航栏背景颜色 */}.nav a {float: left;display: block;text-align: center;padding: 14px 16px;text-decoration: none;color: #000000; /* 导航栏文字颜色 */}.nav a:hover {background-col…...

expected ‘,’ after expression in R【R错误】
出现如下错误: 在红色叉的位置,会有提示“expected . after expression”,咋一看出现红色叉的位置没有任何的错误,怎么会出现错误呢? 解决办法: 寻找这个代码第一次出现红色叉的位置,看其是否…...

算法|图论 2
LeetCode 695- 岛屿的最大面积 题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 题目描述:给你一个大小为 m x n 的二进制矩阵 grid 。 岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求…...

使用C#实现服务端与客户端的简陋聊天
服务端代码: using System; using System.Net.Sockets; using System.Net; using System.IO;//服务器程序 namespace CSharpStudy_09_21 {class Program{static void Main(string[] args){int port 8865;TcpClient tcpClient;//创建tcp对象IPAddress[] serverIp Dns.GetHost…...
生成式模型和判别式模型区别
目录 1.概念 2.定义 3.举例 (1)例子 A (2)例子 B 4.特点 5.优缺点 6.代表算法 1.概念 首先我们需要明确,两种不同的模型都用于监督学习任务中。监督学习的任务就是从数据中学习一个模型,并用…...

【kafka实战】03 SpringBoot使用kafka生产者和消费者示例
本节主要介绍用SpringBoot进行开发时,使用kafka进行生产和消费 一、引入依赖 <dependencies><dependency><groupId>org.springframework.kafka</groupId><artifactId>spring-kafka</artifactId></dependency><depen…...
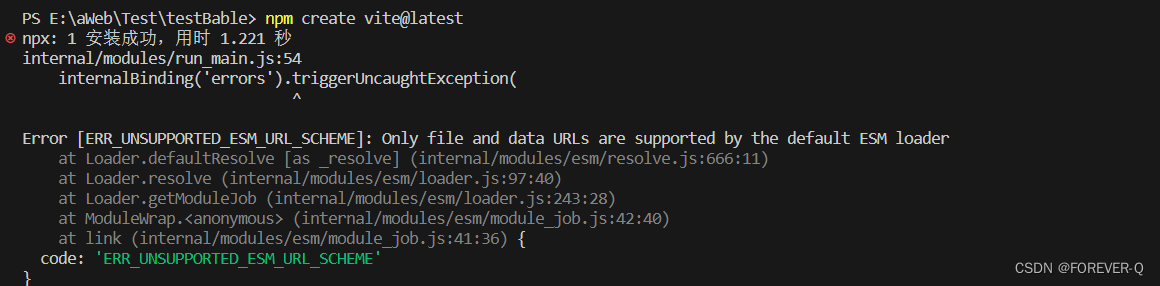
Only file and data URLs are supported by the default ESM loader
1.版本问题 说明:将node版本提高就可以了。 2.nvm 说明:如果不想重复安装node版本,那么可以参考本人的nvm文档. nvm版本控制工具_FOREVER-Q的博客-CSDN博客...
LeetCode01
LeetCode01 两数之和 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和 为目标值 target 的那两个整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。 你…...

计算机网络高频面试题集锦
问题1:谈一谈对OSI七层模型和TCP/IP四层模型的理解? 回答点:七层模型每层对应的作用及相关协议、为什么分层、为什么有TCP/IP四层模型 参考: 1、OSI七层参考模型是一个ISO组织所提出的一个标准参考分层模型,它按照数…...
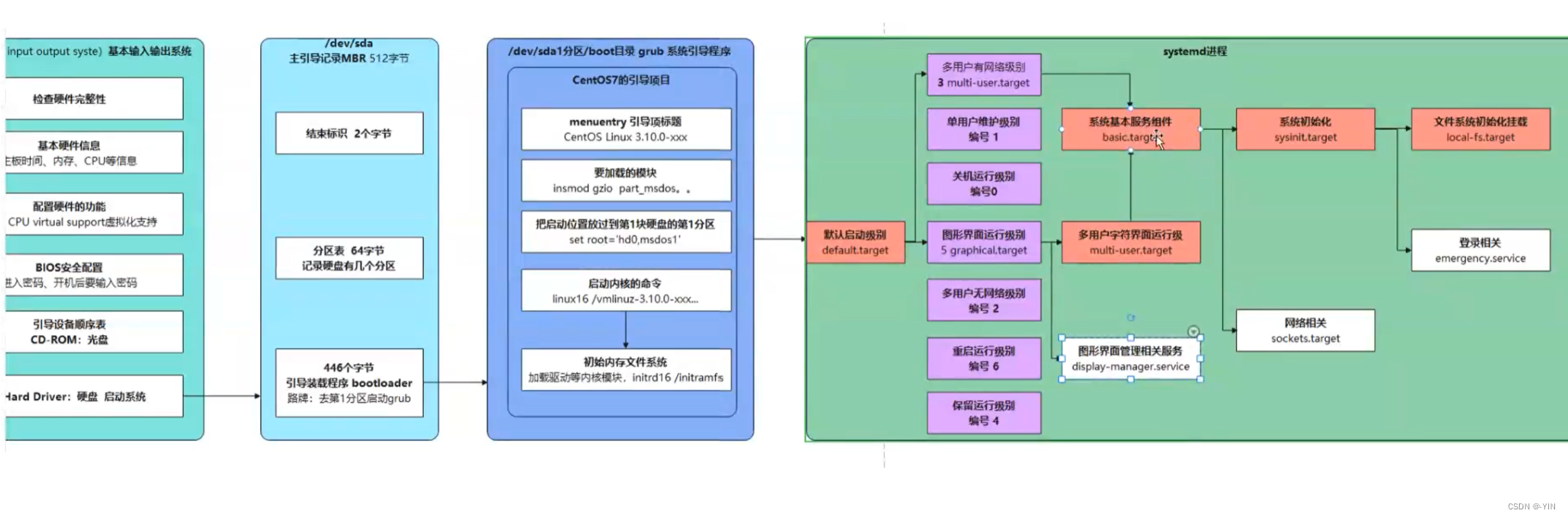
Linux启动过程详解 Xmind导图笔记
参考大佬博客: 简要描述linux系统从开机到登陆界面的启动过程 Linux启动过程详解 Bootloader详解 来源:从BIOS开始画图了解Linux启动过程——老杨Linux...

Qt5开发及实例V2.0-第十七章-Qt版MyWord字处理软件
Qt5开发及实例V2.0-第十七章-Qt版MyWord字处理软件 第17章-Qt版MyWord字处理软件17.1 运行界面17.1.1 菜单设计基本操作17.1.2.MyWord系统菜单 17.2 工具栏设计17.2.1 与菜单对应的工具条17.2.2 附加功能的工具条 这段代码的作用是加载系统标准字号集,只要在主窗体构…...

机器视觉工程师们,常回家看看
我们在这个社会上扮演着多重角色,有时候我们很难平衡好这些角色之间的关系。 人们常言,积善成德,改变命运。善修者,懂得积累,懂得改变命运的重要性。 我曾年少不知父母之不易。一路依靠,一路成长。 所谓…...

网络隔离下实现的文件传输,现有的方式真的安全吗?
在当今的信息化时代,网络安全已经成为了各个企业和机构不可忽视的问题。为了保护内部数据和系统不受外部网络的攻击和泄露,一些涉及国家安全、商业机密、个人隐私等敏感信息的企业和机构,通常会对内外网进行隔离,即建立一个独立的…...
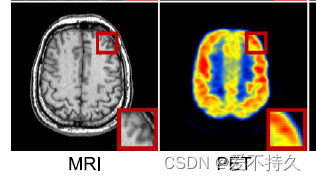
[医学图像知识]CT图和PET图的成像表现形式
1.CT图通常来说是单通道灰色图,用灰度值表示了结构对于x射线的吸收程度。 2.PET/SPECT图最初也是灰度图,用灰度值表示细胞的反射gama射线的程度,但是为了更好的观测不同细胞等的区别,通常将灰度图转化为了 伪彩色图像。 找个例子…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...
