当前位置： 首页 > news >正文

IDEA .iml文件及.idea文件夹详解

news 2026/2/8 9:05:36

.iml文件
idea 对module 配置信息之意， infomation of module。每个模块都有一个iml文件。

IDEA中的.iml文件是项目标识文件，缺少了这个文件，IDEA就无法识别项目。跟Eclipse的.project文件性质是一样的。并且这些文件不同的设备上的内容也会有差异，所以我们在管理项目的时候，.project和.iml文件都需要忽略掉。

iml文件是IntelliJ IDEA自己创建的模块文件，用于java应用开发，存储一些模块相关的信息，比如一个Java组建，插件组建，Maven组建等。存储一些模块路径信息，依赖信息以及别的一些设置。

.idea文件夹：存放项目的配置信息
包括数据源，类库，项目字符编码，历史记录，版本控制信息等。

 其中Artifacts（人工制品，手工制品，手工艺品）是maven中的一个概念，表示某个module要如何打包，例如war exploded、war、jar、ear等等这种打包形式；

inspectionProfiles：检查配置文件

jsLinters：js语法检查配置文件

libraries：类库

 .gitignore：git提交忽略文件

encodings.xml：编码

misc.xml：各种杂项

modules.xml：模块

vcs.xml：版本控制系统

workspace.xml：工作空间。保存着一下项目开发过程中的过程性信息，可以不要。
————————————————
版权声明：本文为CSDN博主「顺其自然~」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/fuhanghang/article/details/108766128

相关文章：

IDEA .iml文件及.idea文件夹详解

.iml文件 idea 对module 配置信息之意， infomation of module。每个模块都有一个iml文件。 IDEA中的.iml文件是项目标识文件，缺少了这个文件，IDEA就无法识别项目。跟Eclipse的.project文件性质是一样的。并且这些文件不同的设备上的内容也会…...

编程日记 2023/9/23 19:42:15

使用Python做一个微信机器人

介绍 简介 该程序将微信的内部功能提取出来，然后在程序里加载Python，接着将这些功能导出成库函数，就可以在Python里使用这些函数 程序启动的时候会执行py_code目录下的main.py，类似于你在命令行使用python main.py。 现在会以…...

编程日记 2023/9/23 19:40:13

云计算战略：选择适合你业务的云平台

文章目录 云计算的概述选择云平台的关键因素1. 业务需求2. 预算3. 性能要求4. 数据隐私和合规性 示例：选择适合的云平台业务需求预算性能要求数据隐私和合规性 代码示例：使用云平台服务结论 🎉欢迎来到云计算技术应用专栏~云计算战略&#xf…...

编程日记 2023/9/23 19:37:10

Python：打印目录下每层的文件总数

代码如下： import osclass FileCount(object):def __init__(self,root_path: str):self.root_path root_pathself._count Noneself._file_count Noneself.children []def get_count(self):if self._count is None:self._count 0self._file_count 0for child_…...

编程日记 2023/9/23 19:35:07

LVS-NAT模式

LVS负载均衡群集 群集的定义 Cluster，集群（也称群集）由多台主机构成，但对外只表现为一一个整体，只提供一-个访问入口(域名或IP地址)， 相当于一台大型计算机。 群集的作用 对于企业服务的的性能提升一般…...

编程日记 2023/9/23 19:34:06

【神印王座】龙皓晨竟然上了头版头条！内容违背，新闻真实性原则

Hello,小伙伴们，我是小郑继续为大家深度解析神印王座国漫。 大家有没有发现，当龙皓晨他们从驱魔关回到圣城时，有这么一幕，一个卖报小孩边走边说：驱魔关大捷，少年英雄龙皓晨操控守护与怜悯之神印王座&#x…...

编程日记 2023/9/23 19:33:06

C++之类和函数权限访问总结(二百二十七)

简介： CSDN博客专家，专注Android/Linux系统，分享多mic语音方案、音视频、编解码等技术，与大家一起成长！ 优质专栏：Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言： 人生…...

编程日记 2023/9/23 19:29:01

手动部署 OceanBase 集群

手动部署一个 OB 单副本集群，包括一个 OBProxy 节点 部署环境 服务器信息 IP地址 192.168.0.26 网卡名 ifcfg-enp1s0 OS Kylin Linux Advanced Server release V10 CPU 8C 内存 32G 磁盘1 本地盘 /data/1 磁盘2 本地盘 /data/log1 机器和角色划分 …...

编程日记 2023/9/23 19:28:00

【操作系统笔记十二】Linux常用基础命令

Linux 常用快捷键 Tab 命令或路径等的补全键，特别常用的快捷键Ctrl insert 复制命令行内容（常用可提高效率）Shift insert 粘贴命令行内容（常用可提高效率）Ctrl C 中断当前任务（退出）Ctrl Z…...

编程日记 2023/9/23 19:26:59

Compose LazyColumn 对比 RecyclerView ，谁的性能更好？

LazyColumn 是 compose 中用来实现类似 RecyclerView 效果的控件 ，但是大家都说LazyColumn性能比RecyclerView差太多，毕竟 RecyclerView google优化了十多年了，比RecyclerView差一点也正常，今天我们就用实际数据来对比LazyColumn和…...

编程日记 2023/9/23 19:24:57

[python 刷题] 49 Group Anagrams

[python 刷题] 49 Group Anagrams 题目： Given an array of strings strs, group the anagrams together. You can return the answer in any order. An Anagram is a word or phrase formed by rearranging the letters of a different word or phrase, typically…...

编程日记 2023/9/23 19:22:54

vue+element plus 使用table组件，清空用户的选择项

<el-table ref"tableRef"> .... </el-table> <script lang"ts" setup> import { onMounted, reactive, ref, nextTick } from vue const clearBtn () > {console.log(清空用户的选择项)tableRef.value.clearSelection() } </scr…...

编程日记 2023/9/23 19:21:53

改写软件-怎么选择改写软件

什么是改写软件&#xff1f;改写软件是基于自然语言处理技术的工具&#xff0c;它们可以分析一段文字&#xff0c;并将其重新表达&#xff0c;以保持原始意义&#xff0c;但使用不同的词汇和结构。这种技术可用于减少内容的重复&#xff0c;增加多样性&#xff0c;或者简化复杂…...

编程日记 2023/9/23 19:18:50

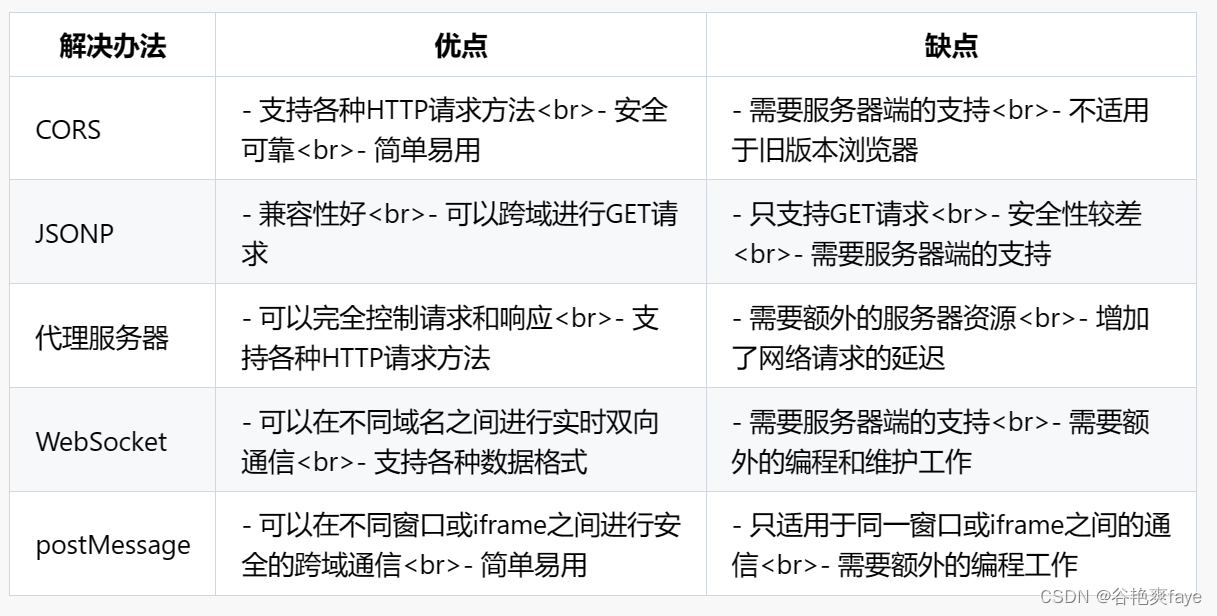
gateway之跨域处理

文章目录 什么是跨域跨域带来的问题 gateway解决跨域解决跨域的其他方式比较代码示例 总结提升 什么是跨域 跨域&#xff08;Cross-Origin&#xff09;是指在浏览器中&#xff0c;当一个Web应用程序试图访问与其所属页面不同的源&#xff08;origin&#xff09;的资源时&#…...

编程日记 2023/9/23 19:16:48

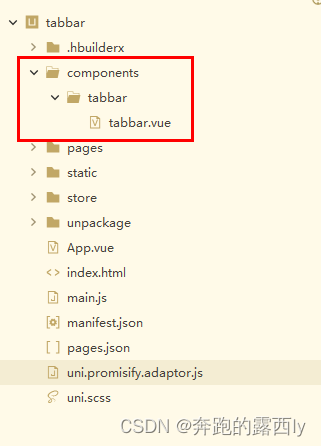
uniapp 实现不同用户展示不同的tabbar(底部导航栏)

一、背景 最近在做一个uniapp开发的小程序遇到一个需求&#xff0c;希望不同用户登录后展示不同的tabbar页面&#xff0c;但是uniapp项目中的pages.json是只有一个list数组的&#xff0c;并且是不能写成动态效果&#xff0c;为了实现这个需求&#xff0c;便自定义了tabbar组件 …...

编程日记 2023/9/23 19:15:47

线性归一化是什么，用python实现数据的线性归一化

线性归一化&#xff08;Linear Normalization&#xff09;是一种常见的数据预处理方法&#xff0c;也被称为 Min-Max 归一化。它通过对原始数据进行线性变换&#xff0c;将其缩放到特定的范围内&#xff0c;常用的是将数据缩放到 [0, 1] 或 [-1, 1] 范围内。 具体来说&#xff…...

编程日记 2023/9/23 19:12:43

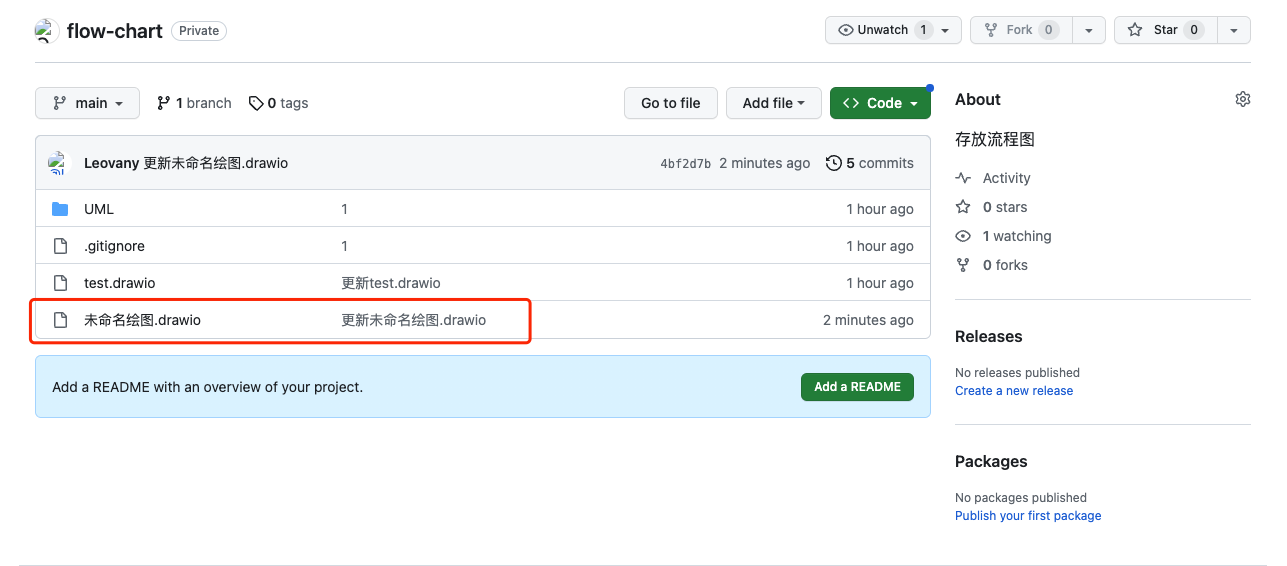
超级好用绘图工具（Draw.io+Github)

超级好用绘图工具&#xff08;Draw.ioGithub&#xff09; 方案简介 绘图工具&#xff1a;Draw.io 存储方式&#xff1a; Github 1 Draw.io 1.2 简介 ​ 是一款免费开源的在线流程图绘制软件&#xff0c;可以用于创建流程图、组织结构图、网络图、UML图等各种类型的图表。…...

编程日记 2023/9/23 19:10:41

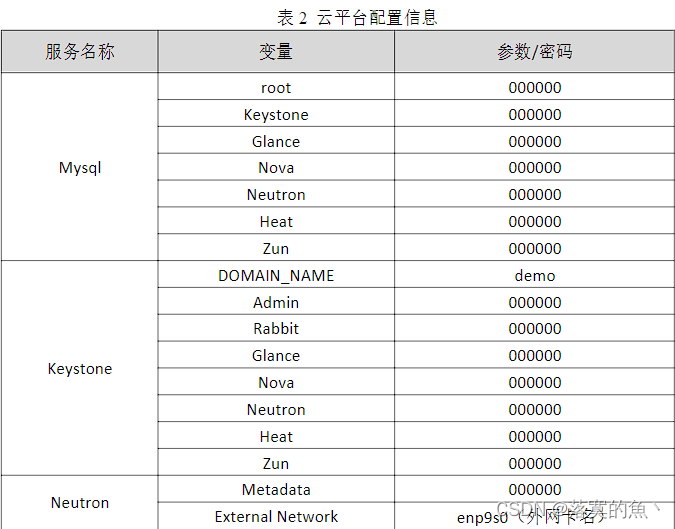
全国职业技能大赛云计算--高职组赛题卷③（私有云）

全国职业技能大赛云计算--高职组赛题卷③&#xff08;私有云&#xff09; 第一场次题目&#xff1a;OpenStack平台部署与运维任务1 基础运维任务&#xff08;5分&#xff09;任务2 OpenStack搭建任务&#xff08;15分&#xff09;任务3 OpenStack云平台运维&#xff08;15分&am…...

编程日记 2023/9/23 19:08:38

Redis SCAN命令操作实战（详细）

目录 SCAN 介绍 SCAN 命令基本用法 MATCH 选项用法 COUNT 选项用法 TYPE 选项用法 补充 并发执行多个迭代 中途停止迭代 使用错误的游标进行增量式迭代 迭代终结的保证 SCAN 介绍 SCAN cursor [MATCH pattern] [COUNT count][TYPE type]&#xff1a;SCAN 命令及其相…...

编程日记 2023/9/23 19:07:37

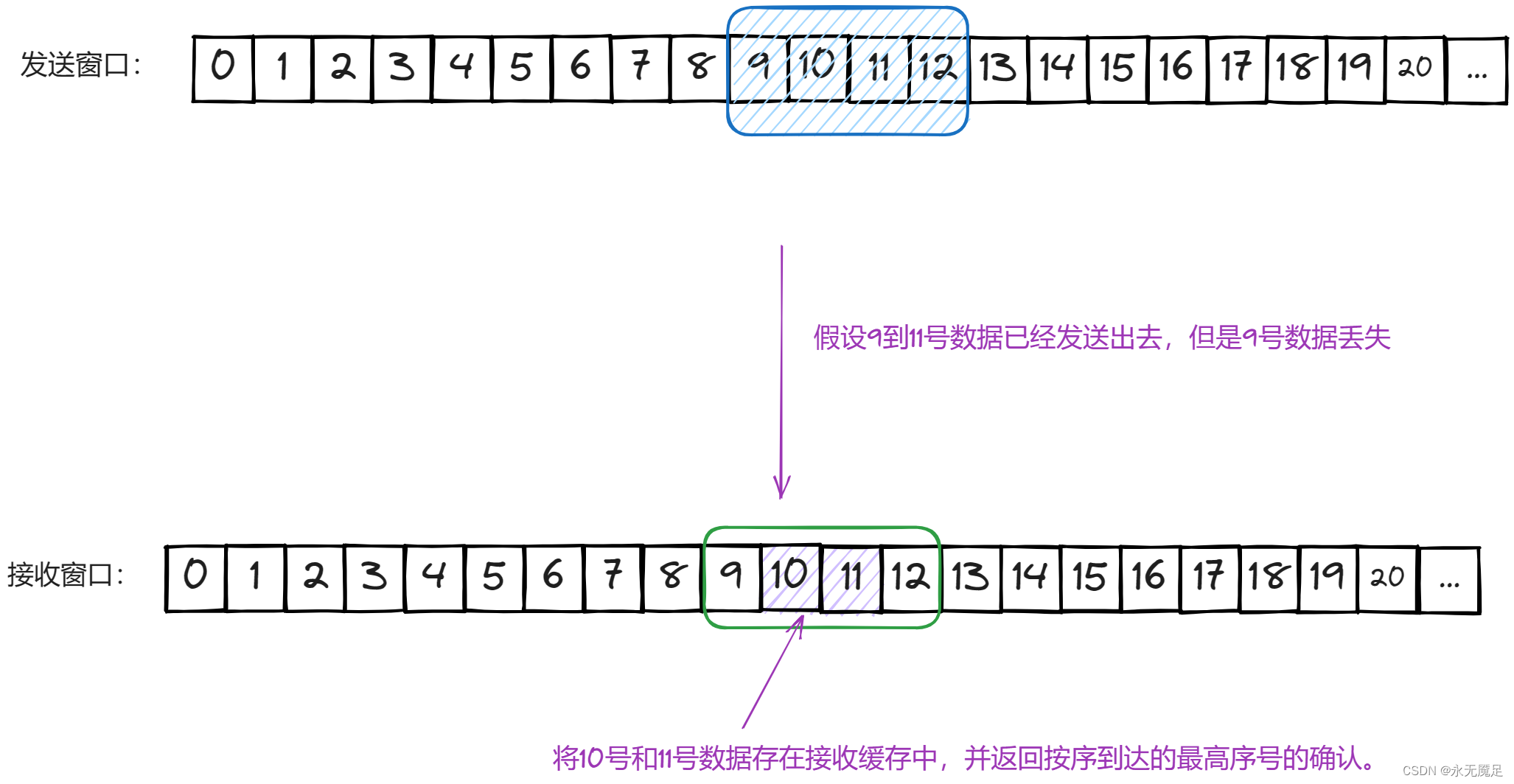
计网第五章（运输层）（六）（TCP可靠传输的实现）

目录 一、基本概述 二、具体实现 1.前后沿&#xff1a; 2.利用指针描述发送窗口的状态 3.有差错情况 之前在数据链路层时已经讨论过可靠传输&#xff08;计网第三章&#xff08;数据链路层&#xff09;&#xff08;二&#xff09;&#xff08;可靠传输&#xff09;&#x…...

编程日记 2023/9/23 19:06:35

华为云Flexus+DeepSeek征文｜DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建

华为云FlexusDeepSeek征文&#xff5c;DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色&#xff0c;华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型&#xff0c;能助力我们轻松驾驭 DeepSeek-V3/R1&#xff0c;本文中将分享如何…...

编程新知 2026/2/2 2:30:58

服务器--宝塔命令

一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行&#xff01; sudo su - 1. CentOS 系统&#xff1a; yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

编程新知 2025/10/3 10:56:48

Selenium常用函数介绍

目录 一&#xff0c;元素定位 1.1 cssSeector 1.2 xpath 二&#xff0c;操作测试对象 三&#xff0c;窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四&#xff0c;弹窗 五&#xff0c;等待 六&#xff0c;导航 七&#xff0c;文件上传 …...

编程新知 2026/1/29 3:55:23

第7篇：中间件全链路监控与 SQL 性能分析实践

7.1 章节导读 在构建数据库中间件的过程中&#xff0c;可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中&#xff0c;必须做到&#xff1a; &#x1f50d; 追踪每一条 SQL 的生命周期&#xff08;从入口到数据库执行&#xff09;&#…...

编程新知 2025/12/11 0:27:15

实战三：开发网页端界面完成黑白视频转为彩色视频

​一、需求描述 设计一个简单的视频上色应用&#xff0c;用户可以通过网页界面上传黑白视频&#xff0c;系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观&#xff0c;不需要了解技术细节。 效果图 ​二、实现思路 总体思路&#xff1a; 用户通过Gradio界面上…...

编程新知 2026/2/5 5:03:25

深度剖析 DeepSeek 开源模型部署与应用：策略、权衡与未来走向

在人工智能技术呈指数级发展的当下&#xff0c;大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性&#xff0c;吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型&#xff0c;成为释放其巨大潜力的关键所在&…...

编程新知 2025/12/27 19:12:07

热烈祝贺埃文科技正式加入可信数据空间发展联盟

2025年4月29日&#xff0c;在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上&#xff0c;可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞&#xff0c;强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...

编程新知 2026/2/7 20:23:55

python学习day39

图像数据与显存 知识点回顾 1.图像数据的格式&#xff1a;灰度和彩色数据 2.模型的定义 3.显存占用的4种地方 a.模型参数梯度参数 b.优化器参数 c.数据批量所占显存 d.神经元输出中间状态 4.batchisize和训练的关系 import torch import torchvision import torch.nn as nn imp…...

编程新知 2026/2/6 23:14:26

RocketMQ 客户端负载均衡机制详解及最佳实践

延伸阅读&#xff1a;&#x1f50d;「RocketMQ 中文社区」 持续更新源码解析/最佳实践&#xff0c;提供 RocketMQ 专家 AI 答疑服务 前言 本文介绍 RocketMQ 负载均衡机制&#xff0c;主要涉及负载均衡发生的时机、客户端负载均衡对消费的影响&#xff08;消息堆积/消费毛刺等…...

编程新知 2026/2/6 11:09:50

智慧城市项目总体建设方案（Word700页+）

1 背景、现状和必要性 1.1 背景 1.1.1 立项背景情况 1.1.2 立项依据 1.2 现状 1.2.1 党建体系运行现状 1.2.2 政务体系运行现状 1.2.3 社会治理运行现状 1.2.4 安全监管体系现状 1.2.5 环保体系运行现状 1.2.6 城建体系运行现状 1.2.7 社区体系运行现状 1.2.8 园区…...

编程新知 2026/2/5 5:38:41