非独立随机变量的概率上界估计
目前的概率论或者随机变量书籍过分强调对独立随机变量的大数定律,中心极限定理,遗憾上界的估计。而对于非独立随机变量的研究很少,在《概率论的极限定理》中曾给出过一般随机变量求和的渐进分布簇的具体形式,然而形式却太过复杂。下面将以切比雪夫不等式为基本出发点,研究非独立情况下的随机变量均值的一个误差上界,为后面研究提供基础。
(非独立随机变量概率误差上界) 若对于随机变量 { r t + 1 , r t + 1 , . . . , r t + n } \{r_{t+1},r_{t+1},...,r_{t+n}\} {rt+1,rt+1,...,rt+n},存在 D max ≥ 0 D_{\max}\geq0 Dmax≥0使得对于任意 k k k,有 D [ r t + k ∣ H k ] ≤ D max \mathbb{D}[r_{t+k}|H_k]\leq D_{\max} D[rt+k∣Hk]≤Dmax,则有下面的式子成立,对于给定 ε > 0 \varepsilon >0 ε>0:
P [ ∣ 1 n ∑ k = 1 n r t + k − 1 n ∑ k = 1 n E t + k [ r t + k ∣ H k ] ∣ > ε ] ≤ D [ ∑ k = 1 n r t + k ∣ H n ] n 2 ε 2 = ∑ k = 1 n D [ r t + k ∣ H n ] + ∑ i = 1 n ∑ j ≠ i n [ E [ r t + i r t + j ∣ H n ] − E [ r t + i ∣ H n ] E [ r t + j ∣ H n ] n 2 ε 2 = ∑ k = 1 n D [ r t + k ∣ H n ] + ∑ i = 1 n ∑ j ≠ i n ρ i j D [ r t + i ∣ H n ] D [ r t + j ∣ H n ] n 2 ε 2 = D max n + ∑ i = 1 n ∑ j ≠ i ρ i j n 2 ε 2 \mathbb{P}[|\frac{1}{n}\sum_{k=1}^nr_{t+k}-\frac{1}{n}\sum_{k=1}^n\mathbb{E}_{t+k}[r_{t+k}|H_k]|>\varepsilon]\leq \frac{\mathbb{D}[\sum_{k=1}^nr_{t+k}|H_n]}{n^2\varepsilon^2}\\ =\frac{\sum_{k=1}^n\mathbb{D}[r_{t+k}|H_n]+\sum_{i=1}^n\sum_{j\ne i}^n[\mathbb{E}[r_{t+i}r_{t+j}|H_n]-\mathbb{E}[r_{t+i}|H_n]\mathbb{E}[r_{t+j}|H_n]}{n^2\varepsilon^2}\\ = \frac{\sum_{k=1}^n\mathbb{D}[r_{t+k}|H_n]+\sum_{i=1}^n\sum_{j\ne i}^n\rho_{ij}\sqrt{\mathbb{D}[r_{t+i}|H_n]}\sqrt{\mathbb{D}[r_{t+j}|H_n]}}{n^2\varepsilon^2}\\=D_{\max}\frac{n+\sum_{i=1}^n\sum_{j\ne i}\rho_{ij}}{n^2\varepsilon^2} P[∣n1k=1∑nrt+k−n1k=1∑nEt+k[rt+k∣Hk]∣>ε]≤n2ε2D[∑k=1nrt+k∣Hn]=n2ε2∑k=1nD[rt+k∣Hn]+∑i=1n∑j=in[E[rt+irt+j∣Hn]−E[rt+i∣Hn]E[rt+j∣Hn]=n2ε2∑k=1nD[rt+k∣Hn]+∑i=1n∑j=inρijD[rt+i∣Hn]D[rt+j∣Hn]=Dmaxn2ε2n+∑i=1n∑j=iρij
其中 ρ i j ∈ [ − 1 , 1 ] \rho_{ij}\in[-1,1] ρij∈[−1,1],表示随机变量 r t + i r_{t+i} rt+i和随机变量 r t + j r_{t+j} rt+j的相关系数,描述了其相关程度。
(推论1) 可以看出的是,若相关性最强的情况,对于任意两个随机变量 r t + i r_{t+i} rt+i和 r t + j r_{t+j} rt+j间都是强相关的,即对于任意 r t + i , r t + j r_{t+i},r_{t+j} rt+i,rt+j, ρ i j = 1 \rho_{ij}=1 ρij=1,则有对于给定的 ε > 0 \varepsilon >0 ε>0:
P [ ∣ 1 n ∑ k = 1 n r t + k − 1 n ∑ k = 1 n E t + k [ r t + k ∣ H k ] ∣ > ε ] ≤ D max ε 2 \mathbb{P}[|\frac{1}{n}\sum_{k=1}^nr_{t+k}-\frac{1}{n}\sum_{k=1}^n\mathbb{E}_{t+k}[r_{t+k}|H_k]|>\varepsilon]\leq \frac{D_{\max}}{\varepsilon^2} P[∣n1k=1∑nrt+k−n1k=1∑nEt+k[rt+k∣Hk]∣>ε]≤ε2Dmax
(推论2) 非独立随机变量若想要使得 大数定律成立,即 1 n ∑ k = 1 n r t + k \frac{1}{n}\sum_{k=1}^nr_{t+k} n1∑k=1nrt+k依概率收敛到 1 n ∑ k = 1 n E t + k [ r t + k ] \frac{1}{n}\sum_{k=1}^n\mathbb{E}_{t+k}[r_{t+k}] n1∑k=1nEt+k[rt+k],则需要使得 ∑ j ≠ i ρ i j < o ( n ) \sum_{j\ne i}\rho_{ij}<o(n) ∑j=iρij<o(n)或者 ∑ i = 1 n ∑ j ≠ i ρ i j < o ( n 2 ) \sum_{i=1}^n\sum_{j\ne i}\rho_{ij}<o(n^2) ∑i=1n∑j=iρij<o(n2) 。
即对于任意一个随机变量 r t + i r_{t+i} rt+i而言,其同其他随机变量 r t + j r_{t+j} rt+j的相关程度之和应该大于 n n n的线性增加。例如:随着 n n n的增加, r t + i r_{t+i} rt+i永远只有和其有限个 m m m的 r t + i − 1 , r t + i − 2 , . . . r t + i − m r_{t+i-1},r_{t+i-2},...r_{t+i-m} rt+i−1,rt+i−2,...rt+i−m相关,则此时大数定律依然成立。
(推论3) 若对于任意 ρ i j , i ≠ j \rho_{ij},i\ne j ρij,i=j, ∣ ρ i j ∣ < ρ ≤ 1 |\rho_{ij}|<\rho\leq1 ∣ρij∣<ρ≤1,则可以得到: P [ ∣ 1 n ∑ k = 1 n r t + k − 1 n ∑ k = 1 n E t + k [ r t + k ∣ H k ] ∣ > ε ] ≤ D max ∣ ρ ∣ ε 2 + D max ( 1 − ∣ ρ ∣ ) n ε 2 \mathbb{P}[|\frac{1}{n}\sum_{k=1}^nr_{t+k}-\frac{1}{n}\sum_{k=1}^n\mathbb{E}_{t+k}[r_{t+k}|H_k]|>\varepsilon]\leq \frac{D_{\max}|\rho|}{\varepsilon^2}+\frac{D_{\max}(1-|\rho|)}{n\varepsilon^2} P[∣n1k=1∑nrt+k−n1k=1∑nEt+k[rt+k∣Hk]∣>ε]≤ε2Dmax∣ρ∣+nε2Dmax(1−∣ρ∣)
进一步可以由极限的保号性可以得到: lim n → ∞ P [ ∣ 1 n ∑ k = 1 n r t + k − 1 n ∑ k = 1 n E t + k [ r t + k ∣ H k ] ∣ > ε ] ≤ D max ∣ ρ ∣ ε 2 \lim_{n\rightarrow \infty} \mathbb{P}[|\frac{1}{n}\sum_{k=1}^nr_{t+k}-\frac{1}{n}\sum_{k=1}^n\mathbb{E}_{t+k}[r_{t+k}|H_k]|>\varepsilon]\leq\frac{D_{\max}|\rho|}{\varepsilon^2} n→∞limP[∣n1k=1∑nrt+k−n1k=1∑nEt+k[rt+k∣Hk]∣>ε]≤ε2Dmax∣ρ∣
Proof:设 a n = P [ ∣ 1 n ∑ k = 1 n r t + k − 1 n ∑ k = 1 n E t + k [ r t + k ∣ H k ] ∣ a_n= \mathbb{P}[|\frac{1}{n}\sum_{k=1}^nr_{t+k}-\frac{1}{n}\sum_{k=1}^n\mathbb{E}_{t+k}[r_{t+k}|H_k]| an=P[∣n1∑k=1nrt+k−n1∑k=1nEt+k[rt+k∣Hk]∣,设 lim n → ∞ a n = c 1 \lim_{n\rightarrow \infty} a_n = c_1 limn→∞an=c1, b n = D max ∣ ρ ∣ ε 2 + D max ( 1 − ∣ ρ ∣ ) n ε 2 b_n=\frac{D_{\max}|\rho|}{\varepsilon^2}+\frac{D_{\max}(1-|\rho|)}{n\varepsilon^2} bn=ε2Dmax∣ρ∣+nε2Dmax(1−∣ρ∣),令 c 2 = D max ∣ ρ ∣ ε 2 c_2=\frac{D_{\max}|\rho|}{\varepsilon^2} c2=ε2Dmax∣ρ∣,则: lim n → ∞ b n = c 2 \lim_{n\rightarrow \infty} b_n = c_2 limn→∞bn=c2,由假设可知 a n ≤ b n a_n\leq b_n an≤bn恒成立。待证明 c 1 ≤ c 2 c_1\leq c_2 c1≤c2,下面采用反证法证明:
不妨设 c 1 > c 2 c_1 > c_2 c1>c2,则有:
lim n → ∞ ( a n − b n ) = c 1 − c 2 > 0 \lim_{n\rightarrow \infty}(a_n-b_n)=c_1-c_2>0 n→∞lim(an−bn)=c1−c2>0由极限的保号性: ∃ N \exists N ∃N,当 n > N n>N n>N时有 a n − b n > 0 a_n-b_n>0 an−bn>0,即 a n > b n a_n>b_n an>bn,然而这与条件 a n ≤ b n a_n\leq b_n an≤bn恒成立矛盾,因此得证 c 1 ≤ c 2 c_1\leq c_2 c1≤c2。
(问题) 所以目前一个重要的问题是: ρ i j \rho_{ij} ρij如何进行估计?
相关文章:

非独立随机变量的概率上界估计
目前的概率论或者随机变量书籍过分强调对独立随机变量的大数定律,中心极限定理,遗憾上界的估计。而对于非独立随机变量的研究很少,在《概率论的极限定理》中曾给出过一般随机变量求和的渐进分布簇的具体形式,然而形式却太过复杂。…...

常见电子仪器及其用途
常见电子仪器及其用途包括: 示波器:示波器是一种用途十分广泛、易于使用且功能强大的电子测量仪器。它能把肉眼看不见的电信号变换成看得见的图像,便于我们研究各种电现象的变化过程。示波器可以直接用来测量电信号的波形,是电子…...

配置测试ip、正式ip、本地ip
目的:npm run serve启动本地服务,npm run test打包测试环境,npm run build打包正式环境。 具体做法如下: 一、在项目中新增三个环境的文件 .env.development VITE_BASE_URLhttp://192.168.1.12:8080/ .env.production VITE_…...
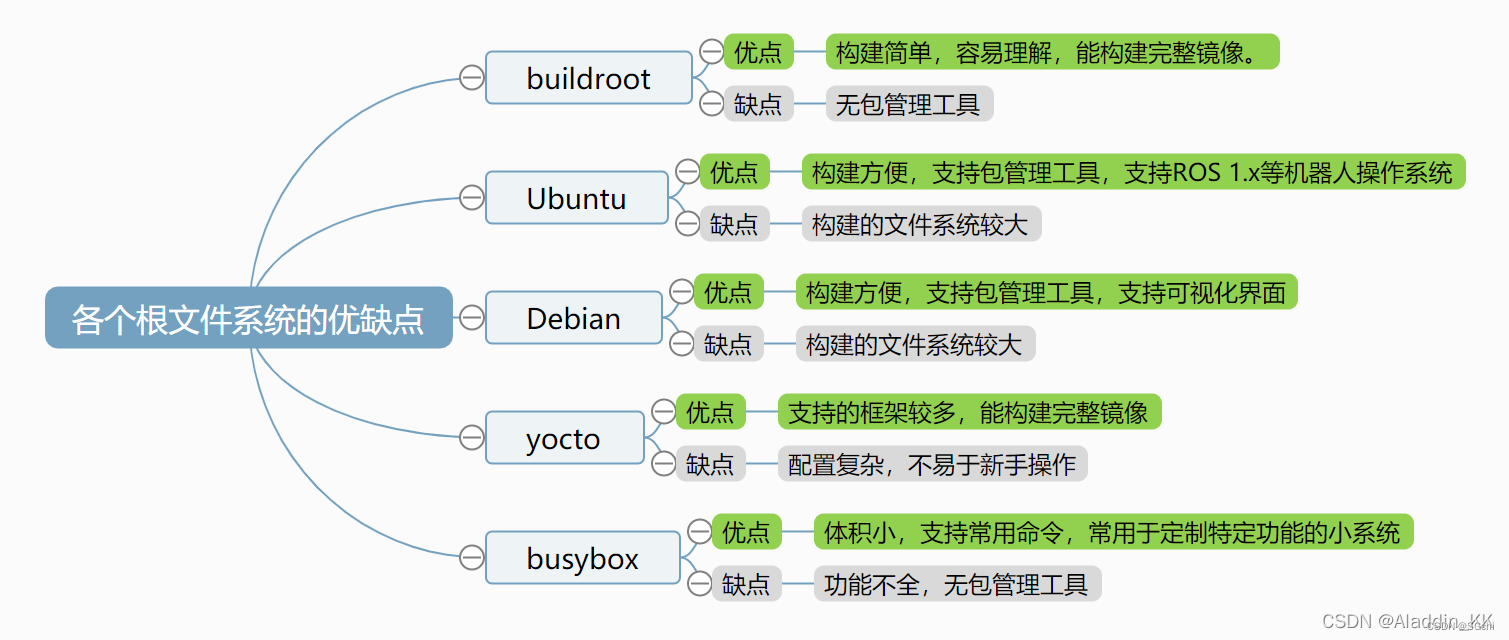
Linux 系统移植(一)-- 系统组成
参考资料: linux系统移植篇(一)—— linux系统组成【野火Linux移植篇】1-uboot初识与编译/烧录步骤 文章目录 一、linux系统组成二、Uboot三、Linux内核四、设备树 本篇为Linux系统移植系列的第一篇文章,介绍了一个完整可运行的L…...

利用git的贮藏功能
可以将自己分支的当前状态贮藏切换到其它分支再切换回来的时候,应用就行了...

第52节:cesium 3DTiles模型特效+选中高亮(含源码+视频)
结果示例: 完整源码: <template><div class="viewer"><vc-viewer @ready="ready" :logo="false"><vc-navigation...
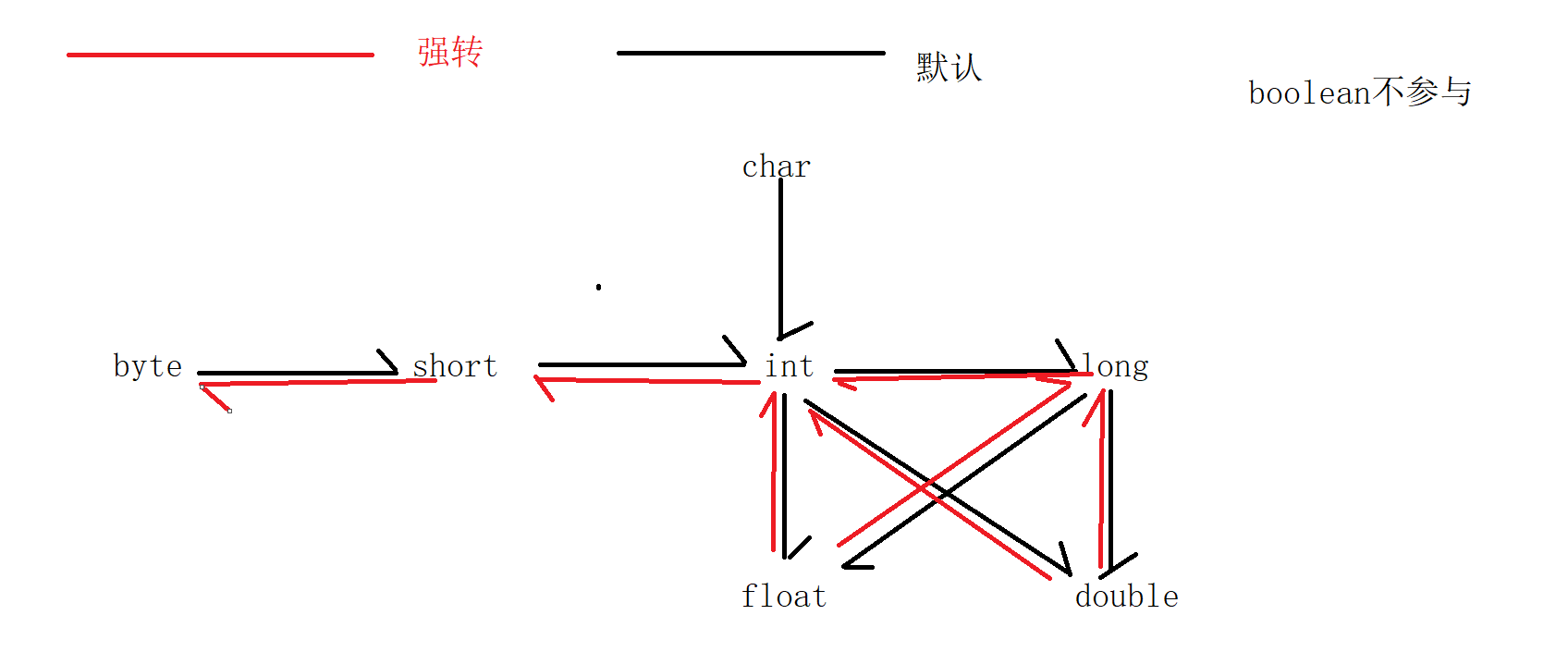
day03_基础语法
今日内容 零、复习昨日 一、Idea安装,配置 二、Idea使用 三、输出语句 四、变量 五、数据类型 附录: 单词 零、 复习昨日 1 装软件(typora,思维导图) 2 gpt(学会让他帮你解决问题) 3 java发展(常识) 4 HelloWorld程序 5 编码规范 6 安装jdk,配置环境变量 电脑常识 任…...
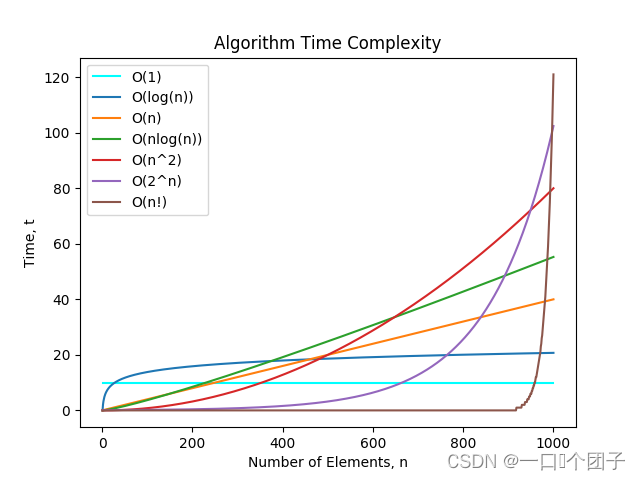
数据结构与算法-时间复杂度与空间复杂度
数据结构与算法 🎈1.概论🔭1.1什么是数据结构?🔭1.2什么是算法? 🎈2.算法效率🔭2.1如何衡量一个算法的好坏?🔭2.2算法的复杂度🔭2.3时间复杂度📖2…...

数组的去重
根据您提供的代码片段,看起来您尝试使用嵌套的 for 循环将数组 data 中的元素添加到新数组 newData 中。然而,在您给出的代码中,if 语句的条件部分为空,可能是因为您还没有确定用于判断重复项的条件。如果您想要去除数组中的重复项…...

Electron自动化测试技术选型调研
Electron简介 Electron是一个开源的框架,用于构建跨平台的桌面应用程序。它由GitHub开发并于2013年首次发布。Electron允许开发人员使用Web技术(如HTML、CSS和JavaScript)来构建桌面应用程序,同时可以在Windows、macOS和Linux等操…...
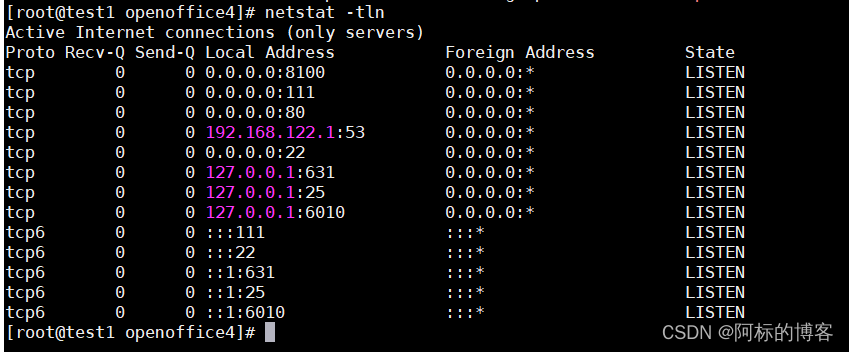
微服务学习(九):安装OpenOffice
微服务学习(九):安装OpenOffice 一、下载OpenOffice 下载地址:OpenOffice 二、开始安装 上传资源到服务器 解压资源包 tar -zxvf Apache_OpenOffice_4.1.13_Linux_x86-64_install-rpm_zh-CN.tar.gz进入zh-CN/RPMS目录下安装…...
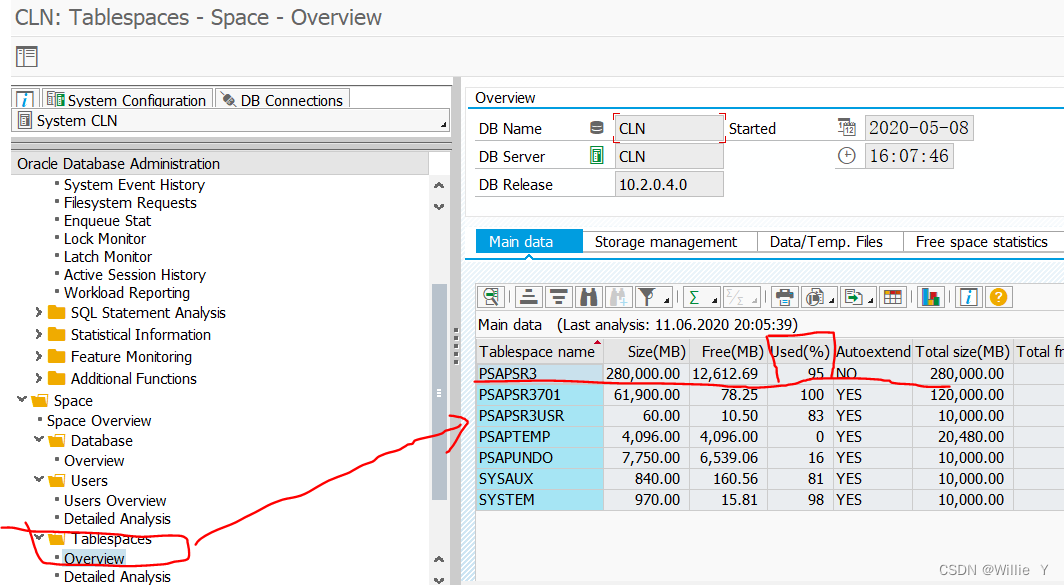
SAP Oracle表空间扩展技术手册
1、DBACOCKPIT下查看表空间 当表空间不足(达到99%)时,需要按以下步骤扩充表空间(每次扩充20000M,20G): (也可以通过DB13,DB02查看表空间) 新浪博客 Tablespace PSAPSR3 is 100% used | SAP Community Oracle是通过增加数据文件的方式来为表空间扩容。为指定表空间增…...

Linux系统编程——线程的学习
学习参考博文: Linux多线程编程初探 Linux系统编程学习相关博文 Linux系统编程——文件编程的学习Linux系统编程——进程的学习Linux系统编程——进程间通信的学习Linux系统编程——网络编程的学习 Linux系统编程——线程的学习 一、概述1. 进程与线程的区别2. 使…...
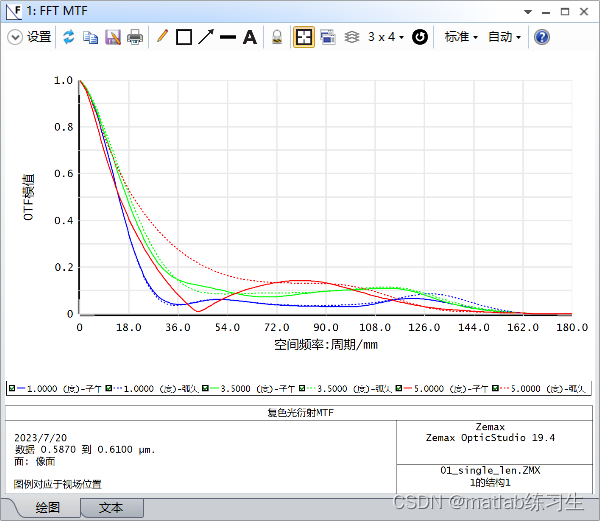
zemaxMIF曲线图
调制传递函数( Modulation Transfer Function,MTF )是用来形容光学系统成像质量的重要指标。 通过对光学系统像空间进行傅里叶变换,可以得到一张分析图表,来描述像面上对比度和空间频率之间的对应关系。 对比度&…...

【苹果】SpringBoot监听Iphone15邮件提醒,Selenium+Python自动化抢购脚本
前言 🍊缘由 Iphone15来了,两年之约你还记得吗? 两年前,与特别的人有一个特别的约定。虽物是人非,但思念仍在。 遂整合之前iphone13及iphone14的相关抢购代码,完成一个SpringBoot监听Iphone15有货邮件提…...
什么是WhatsApp群发,WhatsApp协议,WhatsApp云控
那么WhatsApp群控云控可以做什么呢? 1、获客 自动化引流,强大的可控性,产品快速拓客 2、导流 一键式傻瓜化自动加好友,群发,朋友圈营销 3、群控 一键式拉群好友,建群,进群 …...
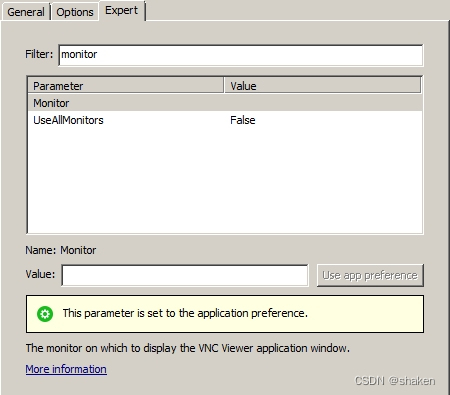
RealVNC viewer 窗口指定默认显示
RealVNC Viewer关于显示器(monitor)的参数有两个,一个是monitor,一个是useallmonitor。 monitor就是指定viewer窗体在哪个显示器上显示的,windows下的默认值是空白,改为\\.\DISPLAY2 就可以在打开远程窗口的时候默认在副屏上显…...
)
图论20(Leetcode1254.统计封闭岛屿的数目)
代码: class Solution {static int[][] dirs {{1,0},{-1,0},{0,1},{0,-1}};public int closedIsland(int[][] grid) {int num 0; for(int i0;i<grid.length;i){for(int j0;j<grid[0].length;j){if(grid[i][j]0){int[] start {i,j};if(getIsland(start,gri…...

Docker 的基本概念和优势,以及在应用程序开发中的实际应用
Docker是一种开源的容器化平台,它可以将应用程序打包成容器,并且可以在不同的环境中运行。Docker的基本概念包括: 镜像(Image):Docker镜像是一个可执行的包,它包含了运行应用程序所需的所有文件…...
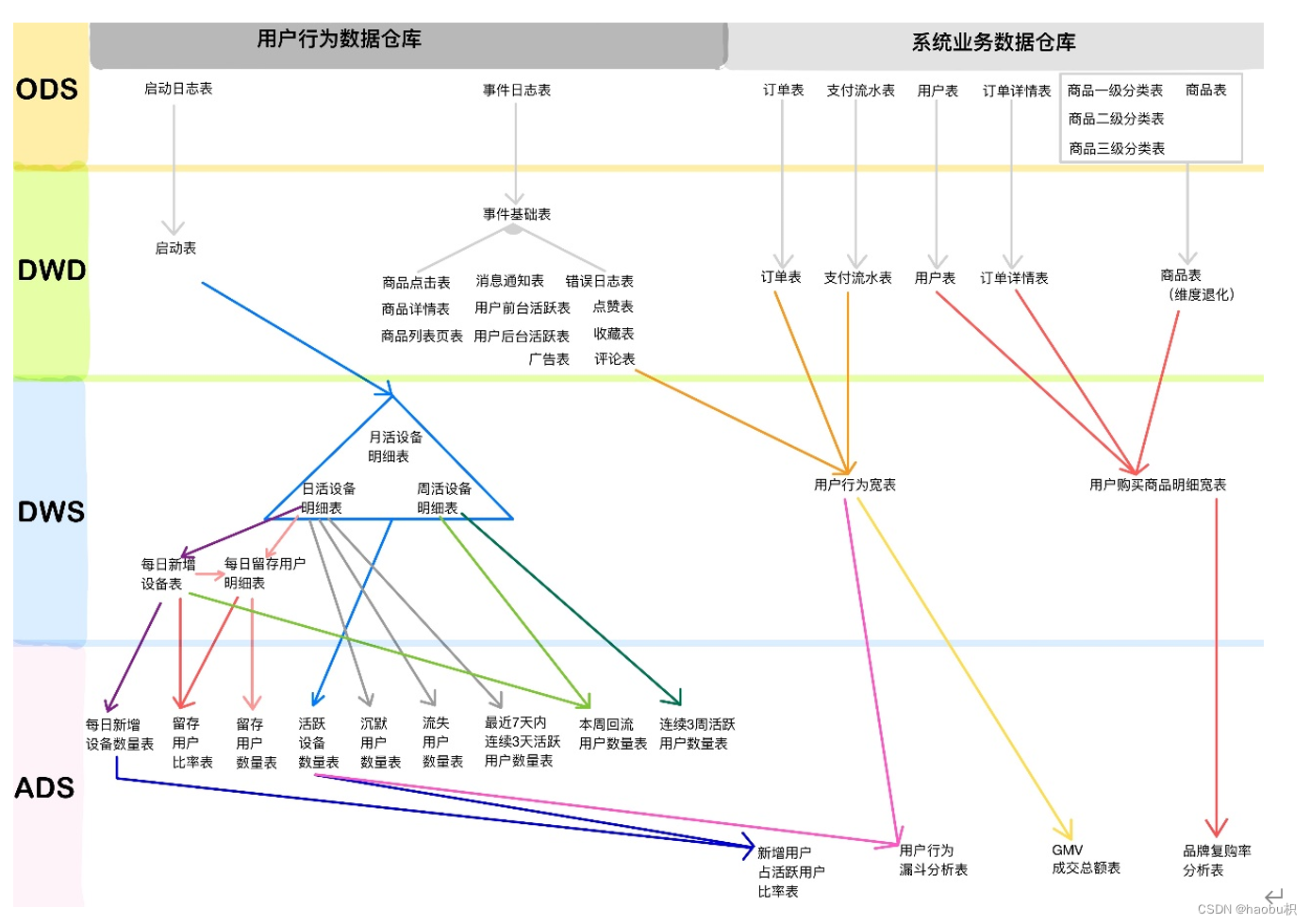
数据仓库整理
数仓 olap vs oltp OLTP主要用于支持日常的业务操作,如银行交易、电子商务等,强调数据的准确性、实时性和并发性。OLAP主要用于支持复杂的数据分析,如数据仓库、决策支持等,强调数据的维度、聚合和可视化。 将OLTP数据库的数据…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...

DAY 45 超大力王爱学Python
来自超大力王的友情提示:在用tensordoard的时候一定一定要用绝对位置,例如:tensorboard --logdir"D:\代码\archive (1)\runs\cifar10_mlp_experiment_2" 不然读取不了数据 知识点回顾: tensorboard的发展历史和原理tens…...

用js实现常见排序算法
以下是几种常见排序算法的 JS实现,包括选择排序、冒泡排序、插入排序、快速排序和归并排序,以及每种算法的特点和复杂度分析 1. 选择排序(Selection Sort) 核心思想:每次从未排序部分选择最小元素,与未排…...

【Qt】控件 QWidget
控件 QWidget 一. 控件概述二. QWidget 的核心属性可用状态:enabled几何:geometrywindows frame 窗口框架的影响 窗口标题:windowTitle窗口图标:windowIconqrc 机制 窗口不透明度:windowOpacity光标:cursor…...

作为点的对象CenterNet论文阅读
摘要 检测器将图像中的物体表示为轴对齐的边界框。大多数成功的目标检测方法都会枚举几乎完整的潜在目标位置列表,并对每一个位置进行分类。这种做法既浪费又低效,并且需要额外的后处理。在本文中,我们采取了不同的方法。我们将物体建模为单…...
