概率论几种易混淆的形式
- 正态分布标准型
x − μ σ \frac{x - \mu}{\sigma} σx−μ
- 大数定律形式
P { X ≤ ∑ i = 1 n x i − n μ n σ 2 } = ∫ − ∞ X 1 2 π e − x 2 2 d x P\{X \le \frac{\sum_{i= 1}^{n}x_i -n\mu}{\sqrt{n\sigma^2}} \} = \int _{-\infty}^{X}\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx P{X≤nσ2∑i=1nxi−nμ}=∫−∞X2π1e−2x2dx
即:
P { X ≤ x ˉ − μ σ n } = ∫ − ∞ X 1 2 π e − x 2 2 d x P\{X \le \frac{\bar x -\mu}{\frac{\sigma}{\sqrt{n}}} \} = \int _{-\infty}^{X}\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx P{X≤nσxˉ−μ}=∫−∞X2π1e−2x2dx
- 关于 χ 2 \chi^2 χ2的定理
( n − 1 ) S 2 σ 2 ∼ χ 2 ( n − 1 ) \frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1) σ2(n−1)S2∼χ2(n−1)
- x ˉ − μ S / n ∼ t 2 ( n − 1 ) \frac{\bar x - \mu}{S/\sqrt{n}} \sim t^2(n-1) S/nxˉ−μ∼t2(n−1)
相关文章:

概率论几种易混淆的形式
正态分布标准型 x − μ σ \frac{x - \mu}{\sigma} σx−μ 大数定律形式 P { X ≤ ∑ i 1 n x i − n μ n σ 2 } ∫ − ∞ X 1 2 π e − x 2 2 d x P\{X \le \frac{\sum_{i 1}^{n}x_i -n\mu}{\sqrt{n\sigma^2}} \} \int _{-\infty}^{X}\frac{1}{\sqrt{2\pi}}e^{-\fr…...

PyTorch数据增强后的结果展示
from PIL import Image import torch from torchvision import transformstrans transforms.Compose([transforms.ToTensor(), transforms.RandomErasing(p0.9, value 120, inplaceTrue)]) # 这里Compose是所做的变换img_path 02-56-45-060-1454-camra1.bmp img Image.open…...

指定程序在哪个GPU上运行
摘要: 当本地(或服务器)有个多个GPU时,需要指定程序在指定GPU上运行,需要做以下设置。 目录 一、在终端上指定GPU二、在程序中指定GPU三、系统变量指定GPU四、pytorch中指定GPU 一、在终端上指定GPU 在终端运行程序时…...

Linux CentOS7 vim多文件编辑
使用vim编辑多个文件,十分常用的操作。本文从打开、显示、切换文件到退出,进行简单讨论。 一、打开文件 1.一次打开多个文件 vim还没有启动的时候,在终端里输入vim file1 file2 … filen便可以打开所有想要打开的文件。 执行命令 vim fil…...

PAT甲级真题1153: 解码PAT准考证
🕺作者: 主页 我的专栏C语言从0到1探秘C数据结构从0到1探秘Linux菜鸟刷题集 😘欢迎关注:👍点赞🙌收藏✍️留言 🏇码字不易,你的👍点赞🙌收藏❤️关注对我真的…...

linux信号
title: linux信号 createTime: 2020-10-29 18:05:52 updateTime: 2020-10-29 18:05:52 categories: linux tags: SIGHUP 终止进程 终端线路挂断[喝小酒的网摘]http://blog.hehehehehe.cn/a/16999.htm SIGINT 终止进程 中断进程 SIGQUIT 建立CORE文件终止进程,并且生…...

JavaWeb开发-05-SpringBootWeb请求响应
一.请求 1.Postman 2.简单参数 package com.wjh.controller;import org.springframework.web.bind.annotation.RequestMapping; import org.springframework.web.bind.annotation.RestController;import javax.servlet.http.HttpServletRequest;/** 测试请求参数接受*/ R…...

Ubuntu下载
参考文档: 镜像文件:VMware下安装ubuntu 16.04(全步骤)_vmwaubuntu-16.04.4-desktop-amd64.iso_ST0new的博客-CSDN博客 vmware tools使用安装:VMware——VMware Tools的介绍及安装方法_William.csj的博客-CSDN博客 …...

Vue 的组件加载顺序和渲染顺序
1、结论先行 组件的加载顺序是自上而下的,也就是先加载父组件,再递归地加载其所有的子组件。 而组件渲染顺序是按照深度优先遍历的方式,也就是先渲染最深层的子组件,再依次向上渲染其父组件。 2、案例 下面是一个简单的示例代…...
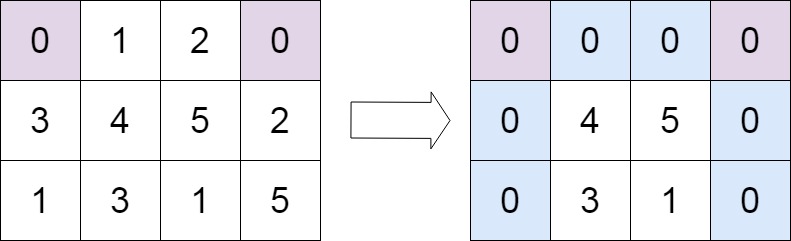
leetcode Top100(17)矩阵置零
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。 示例 1: 输入:matrix [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]]示例 2: 输入&…...
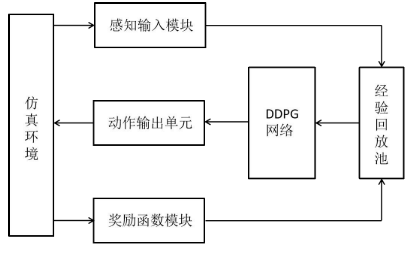
论文精读(2)—基于稀疏奖励强化学习的机械臂运动规划算法设计与实现(内含实现机器人控制的方法)
目录 1.作者提出的问题及解决方向 2.延深-用如何用强化学习对机器人进行控制 2.1思路 2.2DQN和DDPG在机器人控制中的应用 3.解决方案 3.1思路 3.2实验 3.3创新点 4.展望 1.作者提出的问题及解决方向 目的:使机械臂在非结构化环境下实现端到端的自主学习控制…...

快速安装keepalive
快速安装keepalive #安装 yum install keepalived -y# 查看版本: rpm -q -a keepalived#修改配置文件 vim /etc/keepalived.conf虚拟 ip :随意选一个,不被占用的ip即可。...
nginx实现反向代理实例
1 前言 1.1 演示内容 在服务器上访问nginx端口然后跳转到tomcat服务器 1.2 前提条件 前提条件:利用docker安装好nginx、tomcat、jdk8(tomcat运行需要jdk环境) 只演示docker安装tomcat: 默认拉取最新版tomcat docker pull t…...

使用Freemarker填充模板导出复杂Excel,其实很简单哒!
文章目录 1. 需求分析2. 对象生成3. 列表插值4. 另存xml格式化5. ftl修改6. 程序转化7. 犯的错误8. 总结 1. 需求分析 类似这样的一个表格 我们需要从数据库中查询对应的数据,将其汇总进该表格,并且可能还需要复制表格项,我这个案例中没有&a…...

windows环境下安装logstash同步数据,注册系统服务
windows环境下安装logstash同步数据,注册系统服务 此方法适用于Windows环境,同一个配置文件配置多个管道,并且配置系统服务,防止程序被杀进程 一、安装logstash (1)下载压缩包,解压后修改con…...
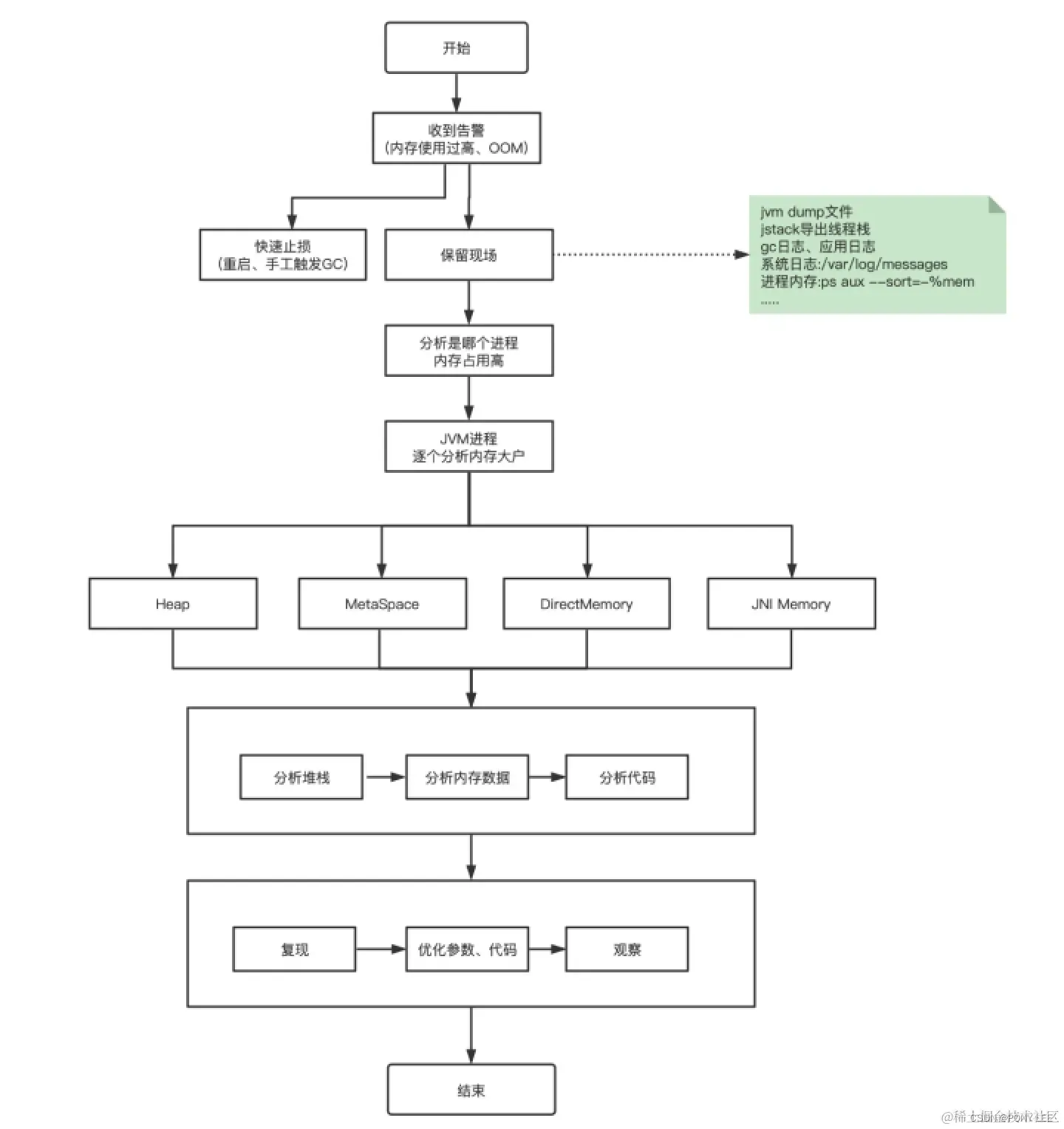
java服务内存说明及配置详解
java进程内存 JVM内存分布图: 【java进程内存】【堆外内存】 【jvm堆内存】 【堆外内存】 【Metaspace】 【Direct Memory】【JNI Memory】【code_cache】 … 堆外内存泄漏的排查在于【本地内存(Native Memory)】【Direct Memory】【JNI Memory】 一般…...
Mybatis-MyBatis的缓存
Mybatis-MyBatis的缓存 一、MyBatis的一级缓存二、MyBatis的二级缓存二级缓存的相关配置 三、MyBatis缓存查询的顺序 一、MyBatis的一级缓存 一级缓存是SqlSession级别的,通过同一个SqlSession查询的数据会被缓存,下次查询相同的数据,就 会从…...
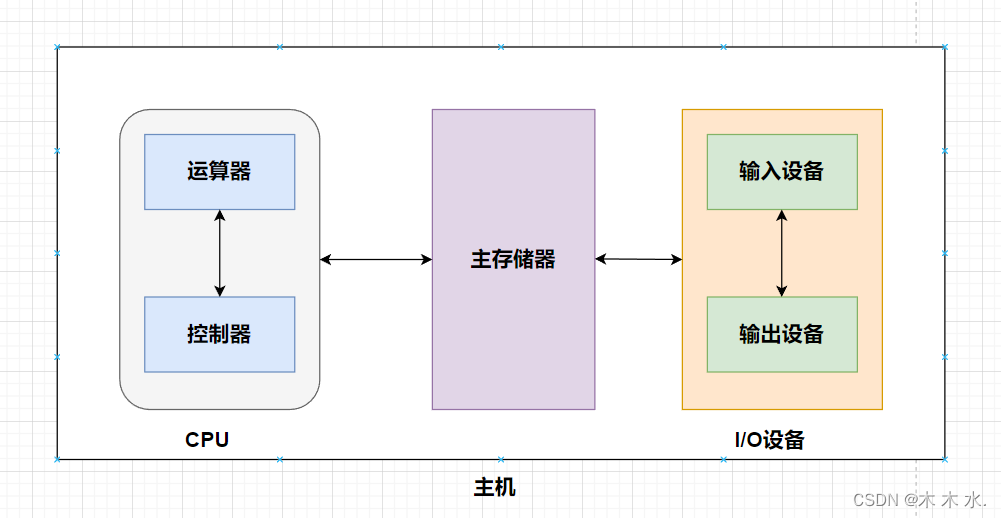
计算机组成原理之硬件的基本组成,深入介绍两大计算机结构体系,从底层出发认识计算机。
大家好,欢迎阅读《计算机组成原理》的系列文章,本系列文章主要的内容是从零学习计算机组成原理,内容通俗易懂,大家好好学习吧!!! 更多的优质内容,请点击以下链接查看哦~~ ↓ ↓ ↓ …...
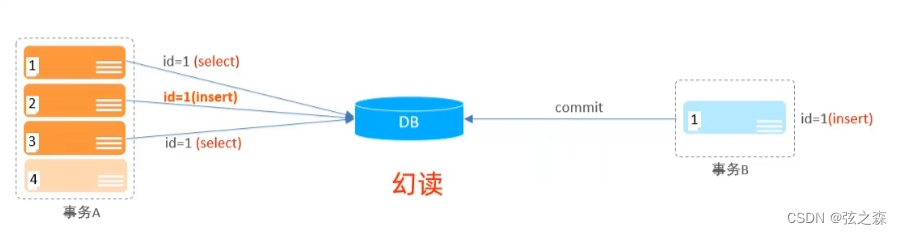
二十五、MySQL事务的四大特性和常见的并发事务问题
1、事务的四大特性 2、常见的并发事务问题 (1)并发事务问题分类: (2)脏读: 一个事务正在对一条记录做修改,在这个事务完成并提交前,这条记录的数据就处于不一致的状态;…...
辨析常见的医学数据分析(相关性分析回归分析)
目录 1 常见的三种分类结果? 2 什么是相关性分析? 相关性分析的结果怎么看? 3 什么是回归分析? 1)前提 2)常见的回归模型 4 对于存在对照组实验的医学病例如何分析? 1)卡方检验…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...
