The 2023 ICPC Asia Regionals Online Contest (1) E. Magical Pair(数论 欧拉函数)
题目
T(T<=10)组样例,每次给出一个n(2<=n<=1e18),
询问多少对,满足
答案对998244353取模,保证n-1不是998244353倍数
思路来源
OEIS、SSerxhs、官方题解
2023 ICPC 网络赛 第一场简要题解 - 知乎
题解
官方题解还没有补,OEIS打了个表然后就通过了
这里给一下SSerxhs教的做法吧(图源:我、tanao学弟)
SSerxhs代码
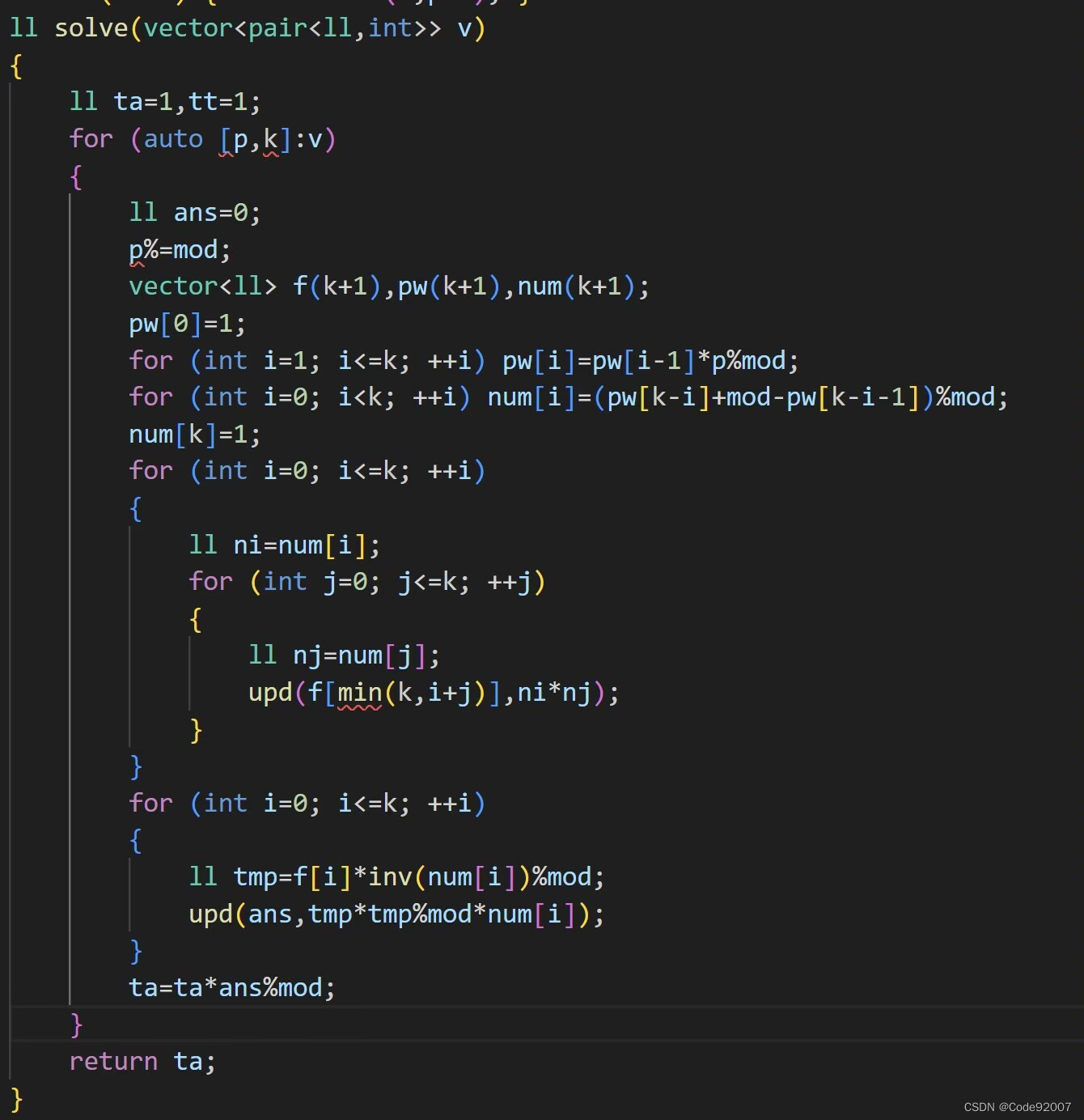
我的理解
首先,证一下这个和是等价的,其中bi为满足
的(x,y)的对数
关于这部分,题解里给的中国剩余定理的构造,也很巧妙

剩下的部分就很神奇了,首先需要注意到各个素因子的贡献是独立的,可以连积

对于求某个素因子的幂次的贡献时,用到了解的分布是均匀的性质

代码1(OEIS)
#include<bits/stdc++.h>
using namespace std;
#define In inline
typedef long long ll;
typedef double db;
const int INF = 0x3f3f3f3f;
const db eps = 1e-8;
map<ll,ll>ans;
inline ll read()
{ll ans = 0;char ch = getchar(), last = ' ';while(!isdigit(ch)) {last = ch; ch = getchar();}while(isdigit(ch)) {ans = (ans << 1) + (ans << 3) + ch - '0'; ch = getchar();}if(last == '-') ans = -ans;return ans;
}
inline void write(ll x)
{if(x < 0) x = -x, putchar('-');if(x >= 10) write(x / 10);putchar(x % 10 + '0');
}ll n;In ll mul(ll a, ll b, ll mod)
{ll d = (long double)a / mod * b + 1e-8; ll r = a * b - d * mod;return r < 0 ? r + mod : r;
}
In ll quickpow(ll a, ll b, ll mod)
{ll ret = 1;for(; b; b >>= 1, a = mul(a, a, mod))if(b & 1) ret = mul(ret, a, mod);return ret;
}In bool test(ll a, ll d, ll n)
{ll t = quickpow(a, d, n);if(t == 1) return 1;while(d != n - 1 && t != n - 1 && t != 1) t = mul(t, t, n), d <<= 1;return t == n - 1;
}
int a[] = {2, 3, 5, 7, 11};
In bool miller_rabin(ll n)
{if(n == 1) return 0;for(int i = 0; i < 5; ++i) {if(n == a[i]) return 1;if(!(n % a[i])) return 0;}ll d = n - 1;while(!(d & 1)) d >>= 1;for(int i = 1; i <= 5; ++i) {ll a = rand() % (n - 2) + 2;if(!test(a, d, n)) return 0;}return 1;
}In ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
In ll f(ll x, ll a, ll mod) {return (mul(x, x, mod) + a) % mod;}
const int M = (1 << 7) - 1;
ll pollard_rho(ll n)
{for(int i = 0; i < 5; ++i) if(n % a[i] == 0) return a[i];ll x = rand(), y = x, t = 1, a = rand() % (n - 2) + 2;for(int k = 2;; k <<= 1, y = x) {ll q = 1;for(int i = 1; i <= k; ++i) {x = f(x, a, n);q = mul(q, abs(x - y), n);if(!(i & M)) {t = gcd(q, n);if(t > 1) break; }}if(t > 1 || (t = gcd(q, n)) > 1) break; }return t;
}
In void find(ll x)
{if(x == 1 ) return;if(miller_rabin(x)) {ans[x]++;return;}ll p = x;while(p == x) p = pollard_rho(x);while(x % p == 0) x/=p;find(p); find(x);
}
const ll mod=998244353;
ll modpow(ll x,ll n){x%=mod;if(!x)return 0;ll res=1;for(;n;n>>=1,x=1ll*x*x%mod){if(n&1)res=1ll*res*x%mod;}return res;
}
ll cal(ll p,ll e){//printf("p:%lld e:%lld\n",p,e);return (modpow(p,e+1)+modpow(p,e)-1+mod)%mod*modpow(p,2*e-1)%mod;
}
int main()
{srand(time(0));int T = read();while(T--){ans.clear();n = read();ll m=n-1;find(m);ll phi=m%mod,res=1;for(auto &v:ans){ll p=v.first,e=0;while(m%p==0)m/=p,e++;res=res*cal(p,e)%mod;}res=(res+phi*phi%mod)%mod;printf("%lld\n",res);}return 0;
}代码2(SSerxhs代码)
#include<bits/stdc++.h>
using namespace std;
#define In inline
typedef long long ll;
typedef double db;
typedef pair<ll,int> P;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
const int INF = 0x3f3f3f3f;
const db eps = 1e-8;
map<ll,int>ans;
vector<P>ans2;
inline ll read()
{ll ans = 0;char ch = getchar(), last = ' ';while(!isdigit(ch)) {last = ch; ch = getchar();}while(isdigit(ch)) {ans = (ans << 1) + (ans << 3) + ch - '0'; ch = getchar();}if(last == '-') ans = -ans;return ans;
}
inline void write(ll x)
{if(x < 0) x = -x, putchar('-');if(x >= 10) write(x / 10);putchar(x % 10 + '0');
}ll n;In ll mul(ll a, ll b, ll mod)
{ll d = (long double)a / mod * b + 1e-8; ll r = a * b - d * mod;return r < 0 ? r + mod : r;
}
In ll quickpow(ll a, ll b, ll mod)
{ll ret = 1;for(; b; b >>= 1, a = mul(a, a, mod))if(b & 1) ret = mul(ret, a, mod);return ret;
}In bool test(ll a, ll d, ll n)
{ll t = quickpow(a, d, n);if(t == 1) return 1;while(d != n - 1 && t != n - 1 && t != 1) t = mul(t, t, n), d <<= 1;return t == n - 1;
}
int a[] = {2, 3, 5, 7, 11};
In bool miller_rabin(ll n)
{if(n == 1) return 0;for(int i = 0; i < 5; ++i) {if(n == a[i]) return 1;if(!(n % a[i])) return 0;}ll d = n - 1;while(!(d & 1)) d >>= 1;for(int i = 1; i <= 5; ++i) {ll a = rand() % (n - 2) + 2;if(!test(a, d, n)) return 0;}return 1;
}In ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
In ll f(ll x, ll a, ll mod) {return (mul(x, x, mod) + a) % mod;}
const int M = (1 << 7) - 1;
ll pollard_rho(ll n)
{for(int i = 0; i < 5; ++i) if(n % a[i] == 0) return a[i];ll x = rand(), y = x, t = 1, a = rand() % (n - 2) + 2;for(int k = 2;; k <<= 1, y = x) {ll q = 1;for(int i = 1; i <= k; ++i) {x = f(x, a, n);q = mul(q, abs(x - y), n);if(!(i & M)) {t = gcd(q, n);if(t > 1) break; }}if(t > 1 || (t = gcd(q, n)) > 1) break; }return t;
}
In void find(ll x)
{if(x == 1 ) return;if(miller_rabin(x)) {ans[x]++;return;}ll p = x;while(p == x) p = pollard_rho(x);while(x % p == 0) x/=p;find(p); find(x);
}
const ll mod=998244353;
ll modpow(ll x,ll n){x%=mod;if(!x)return 0;ll res=1;for(;n;n>>=1,x=1ll*x*x%mod){if(n&1)res=1ll*res*x%mod;}return res;
}
ll cal(ll p,ll e){//printf("p:%lld e:%lld\n",p,e);return (modpow(p,e+1)+modpow(p,e)-1+mod)%mod*modpow(p,2*e-1)%mod;
}
ll sol(){ll ta=1;//tt=1;for(auto &x:ans2){ll p=x.first,ans=0;int k=x.second;p%=mod;vector<ll> f(k+1),pw(k+1),num(k+1);pw[0]=1;rep(i,1,k)pw[i]=pw[i-1]*p%mod;rep(i,0,k-1)num[i]=(pw[k-i]+mod-pw[k-i-1])%mod;num[k]=1;rep(i,0,k){ll ni=num[i];rep(j,0,k){ll nj=num[j];f[min(k,i+j)]=(f[min(k,i+j)]+ni*nj%mod)%mod;}}rep(i,0,k){ll tmp=f[i]*modpow(num[i],mod-2)%mod;ans=(ans+tmp*tmp%mod*num[i]%mod)%mod;}ta=ta*ans%mod;}return ta;
}
int main()
{srand(time(0));int T = read();while(T--){ans.clear();ans2.clear();n = read();ll m=n-1;find(m);//ll phi=m%mod,res=1;for(auto &v:ans){ll p=v.first,e=0;while(m%p==0)m/=p,e++;ans2.push_back(P(p,e));//res=res*cal(p,e)%mod;}m=(n-1)%mod;ll res=sol();res=(res+m*m%mod)%mod;printf("%lld\n",res);//res=(res+phi*phi%mod)%mod;//printf("%lld\n",res);}return 0;
}相关文章:

The 2023 ICPC Asia Regionals Online Contest (1) E. Magical Pair(数论 欧拉函数)
题目 T(T<10)组样例,每次给出一个n(2<n<1e18), 询问多少对,满足 答案对998244353取模,保证n-1不是998244353倍数 思路来源 OEIS、SSerxhs、官方题解 2023 ICPC 网络赛 第一场简要题解 - 知乎 题解 官方题解还没有…...

<十三>objectARX开发:模拟实现CAD的移动Move命令
一、目的 实现类似于CAD的移动命令,选择对象,移动到指定位置,移动过程中对象跟随鼠标移动。效果如下: 二、关键步骤 选择对象,打开实体判断类型:acedEntSel()、acdbOpenObject()、isKindOf()。指定基点:acedGetPoint()。移动模型,追踪光标移动对象实体:acedGrRead()…...

Autosar基础:模式管理-EcuM
ECUM目录 前言一、ECUM状态机二、Fixed和Flexible模式的区别与联系三、状态详解3.1.Startup3.2.UP3.3.RUN3.4.Sleep3.5.Shutdown三、EcuM唤醒源3.1 CAN Trcv唤醒3.2 唤醒后操作前言 根据Autosar对于模式管理的需求定义,模式管理有以下模块: ①ECU State Manager(EcuM):管理…...

代码随想录Day42 | 01背包问题| 416. 分割等和子集
01背包问题(Acwing) 有 N 件物品和一个容量是 V的背包。每件物品只能使用一次。 第 i 件物品的体积是 vi,价值是 wi。 求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。 输出最大价值。 输入…...
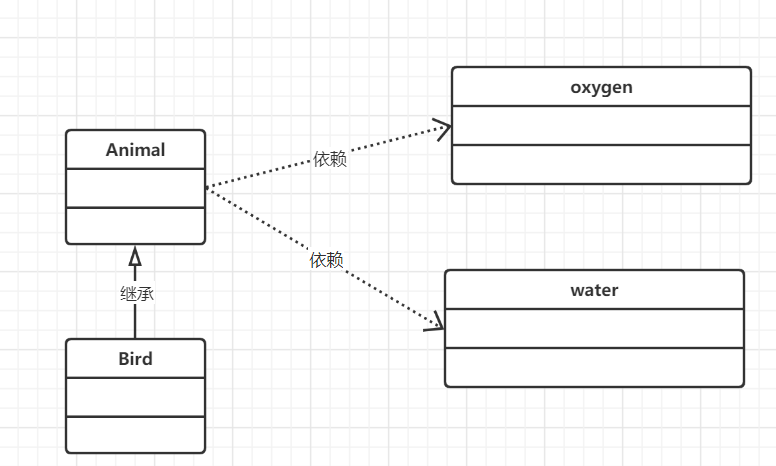
UML六大关系总结
UML六大关系有:继承、关系、聚合、组合、实现、依赖。分为通过图和代码总结这些关系。 1、继承 继承(Inheritance):表示类之间的继承关系,子类继承父类的属性和方法,并可以添加自己的扩展。 继承&#x…...

ElementUI基本介绍及登录注册案例演示
目录 前言 一.简介 二.优缺点 三.Element完成登录注册 1. 环境配置及前端演示 1.1 安装Element-UI模块 1.2 安装axios和qs(发送get请求和post请求) 1.3 导入依赖 2 页面布局 2.1组件与界面 3.方法实现功能数据交互 3.1 通过方法进行页面跳转 3.2 axios发送get请求 …...
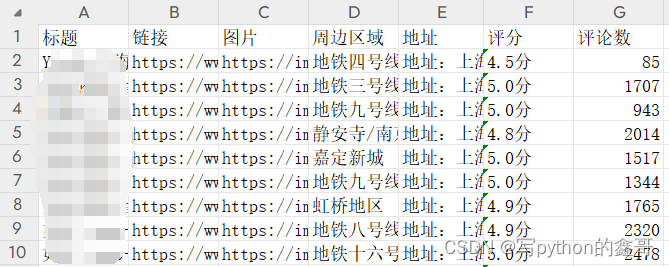
Python爬虫-某网酒店评论数据
前言 本文是该专栏的第6篇,后面会持续分享python爬虫案例干货,记得关注。 本文以某网的酒店数据为例,采集对应酒店的评论数据。具体思路和方法跟着笔者直接往下看正文详细内容。(附带完整代码) 注意:本文的案例“数据集”,选用的是本专栏上一篇“Python爬虫-某网酒店数…...
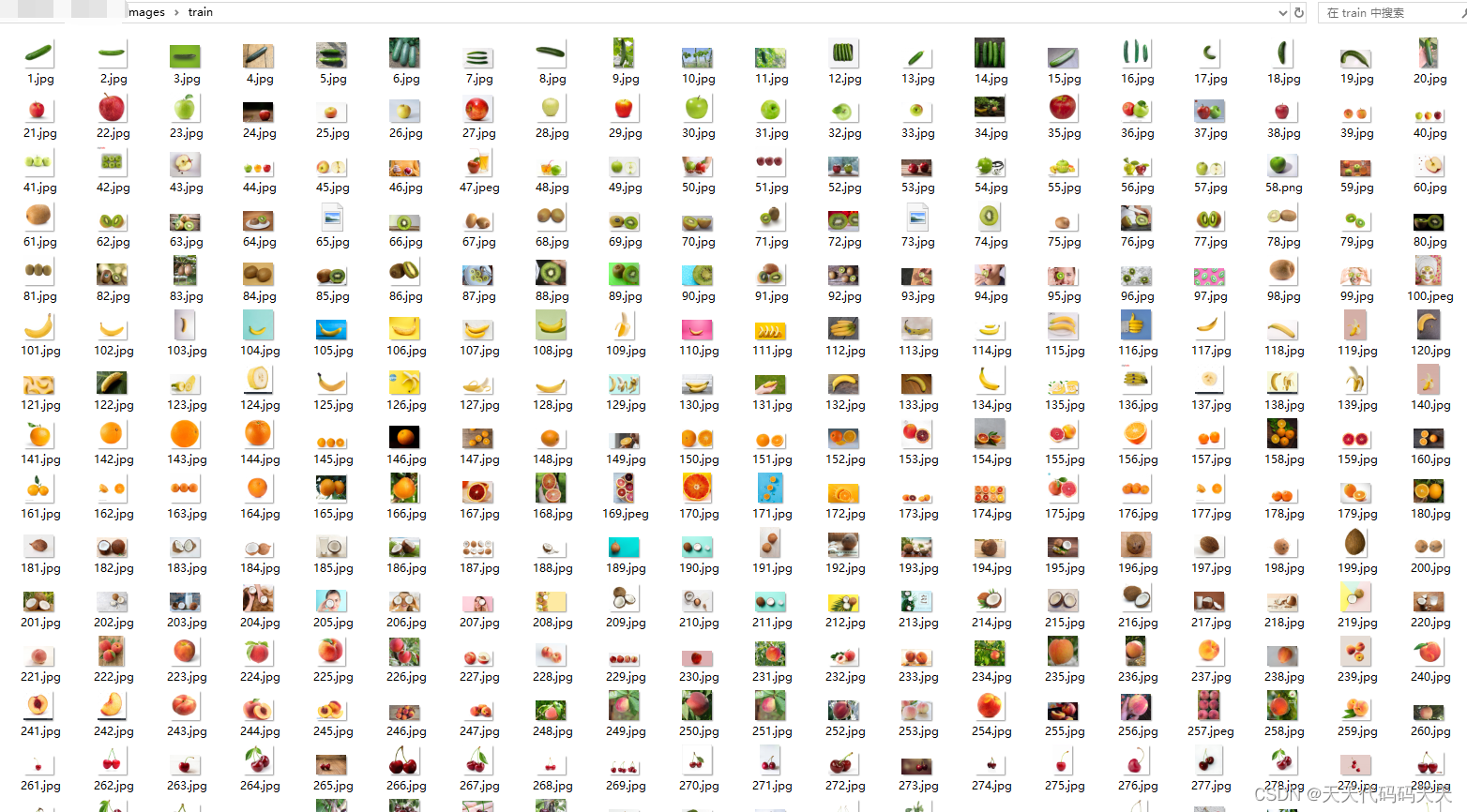
C# Onnx Yolov8 Detect 水果识别
效果 项目 代码 using Microsoft.ML.OnnxRuntime; using Microsoft.ML.OnnxRuntime.Tensors; using OpenCvSharp; using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System…...
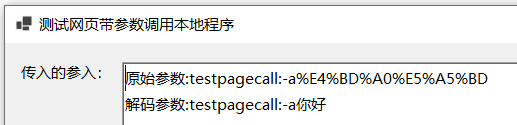
测试网页调用本地可执行程序(续1:解析参数中的中文编码)
学习测试网页调用本地可执行程序还遗留一个问题,即网页中调用带中文参数的命令时,本地可执行程序接收到的参数字符串里的中文都转换成了编码模式,看起来如下所示: <a href TestPageCall:-a你好>启动测试程序</a><…...

C++入门知识
Hello,今天我们分享一些关于C入门的知识,看完至少让你为后面的类和对象有一定的基础,所以在讲类和对象的时候,我们需要来了解一些关于C入门的知识。 什么是C C语言是结构化和模块化的语言,适合处理较小规模的程序。对…...

spring和springmvc常用注解
1.Spring常用注解: 1)Repository将DAO类声明为Bean 2)Service用于修饰service层的组件 3)Controller通常作用在控制层,将在Spring MVC中使用 4)Component是一个泛化的概念,仅仅表示spring中的一…...

【Java】Java生成PDF工具类
Java生成PDF工具类 一、介绍 Java生成PDF工具类是一个非常实用的工具类,可以帮助我们以程序化的方式生成PDF文件。通过该工具类,我们可以向PDF文件中添加文字、图片、表格等多种内容,并且可以进行格式化和样式设置。Java生成PDF工具类常用于…...

STL map,插入和查找的一些注意事项
01、前言(废话) C 的 std::map 容器中插入键值对主要有myMap(std::make_pair(key value)) ,它们的区别你了解吗? auto it myMap,find(key) 和 auto value myMap[key] 都可以用于在 C 的 std::map 容器中查找键对应的值ÿ…...
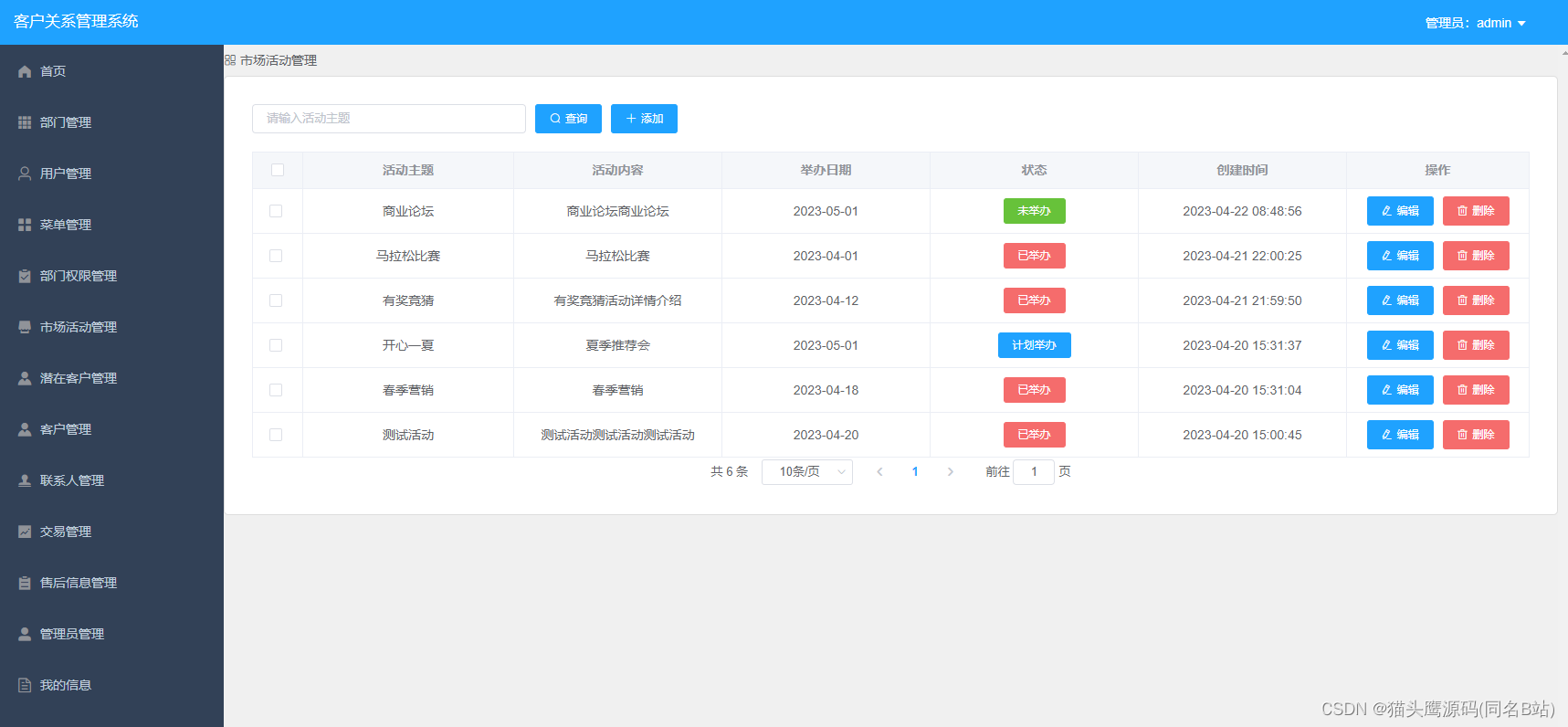
基于springboot+vue的客户关系管理系统(前后端分离)
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…...

【Java 基础篇】Java Stream 流详解
Java Stream(流)是Java 8引入的一个强大的新特性,用于处理集合数据。它提供了一种更简洁、更灵活的方式来操作数据,可以大大提高代码的可读性和可维护性。本文将详细介绍Java Stream流的概念、用法和一些常见操作。 什么是Stream…...

题解:ABC321A - 321-like Checker
题解:ABC321A - 321-like Checker 题目 链接:Atcoder。 链接:洛谷。 难度 算法难度:C。 思维难度:C。 调码难度:C。 综合评价:见洛谷链接。 算法 模拟。 思路 输入n后从后往前依次抽…...
Zig实现Hello World
1. 什么是zig 先列出一段官方的介绍: Zig is a general-purpose programming language and toolchain for maintaining robust, optimal, and reusable software. 大概意思就是说: Zig是一种通用编程语言和工具链,用于维护健壮、最佳和可重用的软件。 官…...
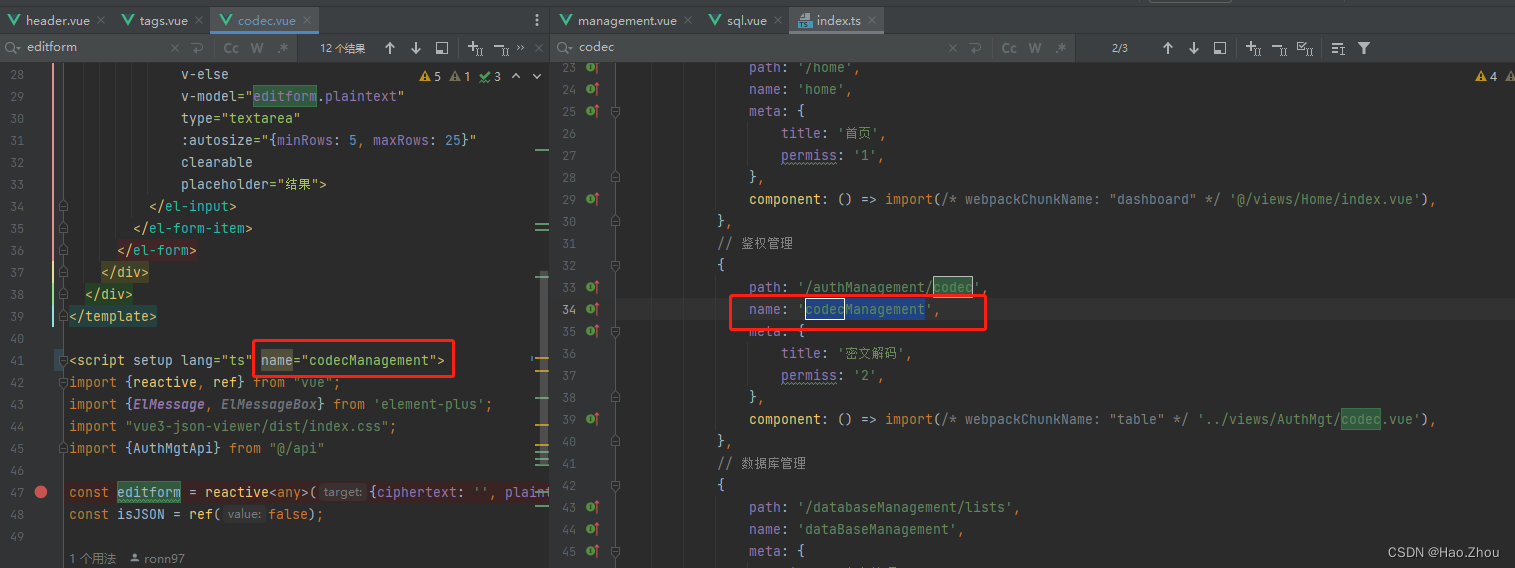
Vue3+element-plus切换标签页时数据保留问题
记录一次切换标签页缓存失效问题,注册路由时name不一致可能会导致缓存失效...

前端教程-TypeScript
官网 TypeScript官网 TypeScript中文官网 视频教程 尚硅谷TypeScript教程(李立超老师TS新课)...
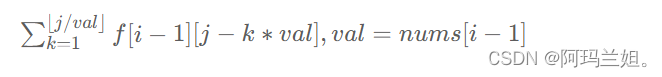
代码随想录算法训练营 动态规划part06
一、完全背包 卡哥的总结,还挺全代码随想录 (programmercarl.com) 二、零钱兑换 II 518. 零钱兑换 II - 力扣(LeetCode) 被选物品之间不需要满足特定关系,只需要选择物品,以达到「全局最优」或者「特定状态」即可。 …...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...
