CSS 小球随着椭圆移动
html代码:
<!DOCTYPE html>
<html lang="en">
<head><meta charset="UTF-8"><meta name="viewport" content="width=device-width, initial-scale=1.0"><title>Document</title><link rel="stylesheet" href="./index.css">
</head>
<body><div class="background-img"><div class="area"><div class="ball ball1"></div><div class="ball ball2"></div><div class="ball ball3"></div><div class="ball ball4"></div><div class="ball ball5"></div><div class="ball ball6"></div><div class="ball ball7"></div><div class="ball ball8"></div></div>
</div>
</body>
</html>css代码:
.background-img {height: 32vw;width: 60%;margin-top: 1vw;text-align: center;
}.area {width: 100%;height: 100%;position: relative;
}.area:hover>.ball {animation-play-state: paused;
}.area>.ball {width: 7.0313vw;height: 7.0313vw;position: absolute;border-radius: 7.0313vw;background-image: linear-gradient(to top, #051F56, #1B8EF8);color: #E1EAFE;
}.area>.ball1 {animation: anmiteX 10s cubic-bezier(0.6, 0.3, 0.3, 0.6) -5s infinite alternate,anmiteY 10s cubic-bezier(0.6, 0.3, 0.3, 0.6) 0s infinite alternate,scale 20s cubic-bezier(0.6, 0.3, 0.3, 0.6) 0s infinite alternate;
}.area>.ball2 {animation: anmiteX 10s cubic-bezier(0.6, 0.3, 0.3, 0.6) -7.5s infinite alternate,anmiteY 10s cubic-bezier(0.6, 0.3, 0.3, 0.6) -2.5s infinite alternate,scale 20s cubic-bezier(0.6, 0.3, 0.3, 0.6) -2.5s infinite alternate;
}.area>.ball3 {animation: anmiteX 10s cubic-bezier(0.6, 0.3, 0.3, 0.6) -10s infinite alternate,anmiteY 10s cubic-bezier(0.6, 0.3, 0.3, 0.6) -5s infinite alternate,scale 20s cubic-bezier(0.6, 0.3, 0.3, 0.6) -5s infinite alternate;
}.area>.ball4 {animation: anmiteX 10s cubic-bezier(0.6, 0.3, 0.3, 0.6) -12.5s infinite alternate,anmiteY 10s cubic-bezier(0.6, 0.3, 0.3, 0.6) -7.5s infinite alternate,scale 20s cubic-bezier(0.6, 0.3, 0.3, 0.6) -7.5s infinite alternate;
}.area>.ball5 {animation: anmiteX 10s cubic-bezier(0.6, 0.3, 0.3, 0.6) -15s infinite alternate,anmiteY 10s cubic-bezier(0.6, 0.3, 0.3, 0.6) -10s infinite alternate,scale 20s cubic-bezier(0.6, 0.3, 0.3, 0.6) -10s infinite alternate;
}.area>.ball6 {animation: anmiteX 10s cubic-bezier(0.6, 0.3, 0.3, 0.6) -17.5s infinite alternate,anmiteY 10s cubic-bezier(0.6, 0.3, 0.3, 0.6) -12.5s infinite alternate,scale 20s cubic-bezier(0.6, 0.3, 0.3, 0.6) -12.5s infinite alternate;
}.area>.ball7 {animation: anmiteX 10s cubic-bezier(0.6, 0.3, 0.3, 0.6) -20s infinite alternate,anmiteY 10s cubic-bezier(0.6, 0.3, 0.3, 0.6) -15s infinite alternate,scale 20s cubic-bezier(0.6, 0.3, 0.3, 0.6) -15s infinite alternate;
}.area>.ball8 {animation: anmiteX 10s cubic-bezier(0.6, 0.3, 0.3, 0.6) -22.5s infinite alternate,anmiteY 10s cubic-bezier(0.6, 0.3, 0.3, 0.6) -17.5s infinite alternate,scale 20s cubic-bezier(0.6, 0.3, 0.3, 0.6) -17.5s infinite alternate;
}/* 动画 *//* 在X轴上的移动 */
@keyframes anmiteX {from {left: 56vw;}to {left: -1vw;}
}/* 在轴上Y的移动 */
@keyframes anmiteY {from {top: 7vw;}to {top: 28vw;}
}/* 对球进行放大和缩小在视觉上进行远近的模拟 */
@keyframes scale {0% {transform: scale(0.8, 0.8);opacity: 0.5;}50% {transform: scale(1.3, 1.3);opacity: 1;}100% {transform: scale(0.8, 0.8);opacity: 0.5;}
}相关文章:

CSS 小球随着椭圆移动
html代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title><…...
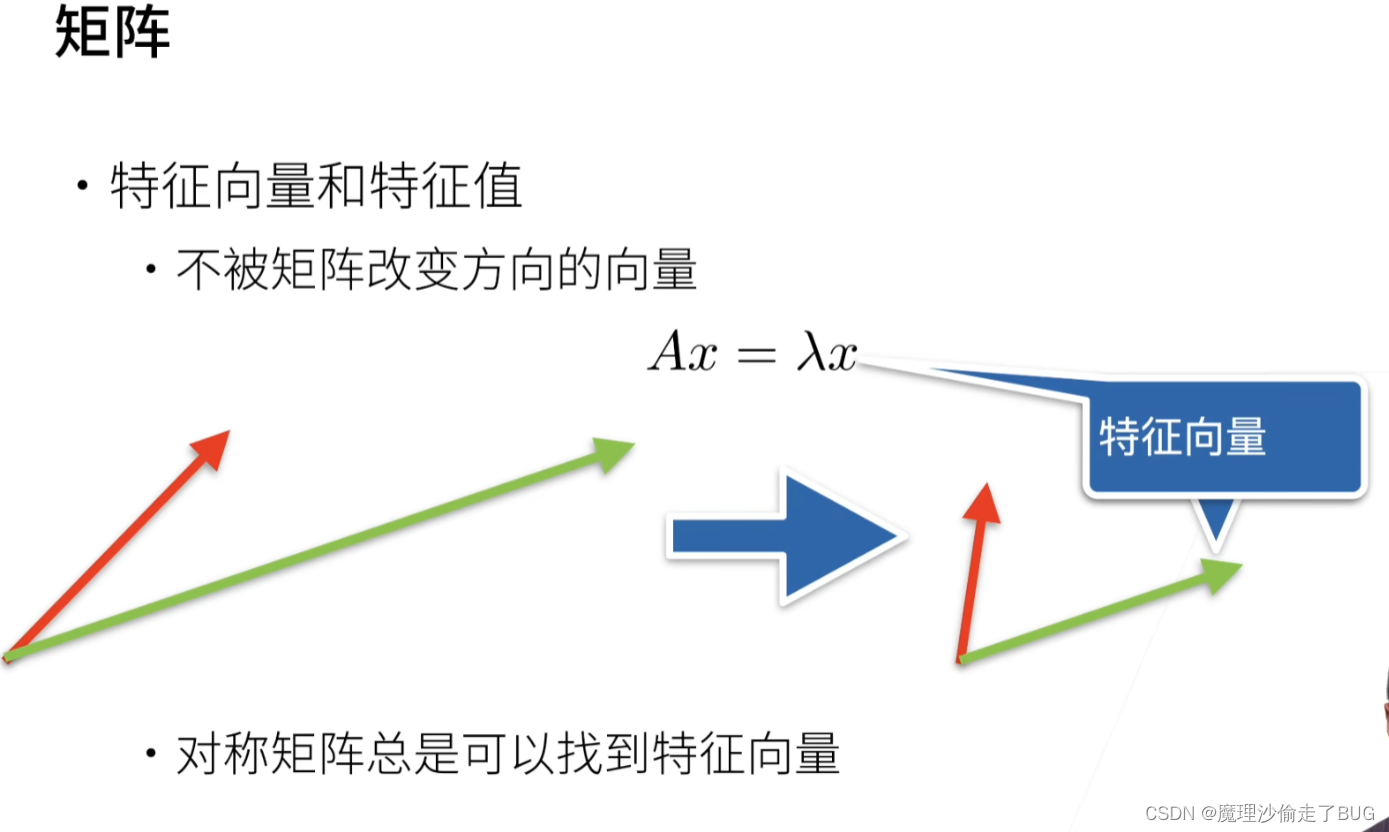
【李沐深度学习笔记】线性代数
课程地址和说明 线性代数p1 本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。 线性代数 标量 标量(scalar),亦称“无向量”。有些物理量,只具有数值大小,…...

vuejs - - - - - 递归组件的实现
递归组件的实现 1. 需求描述:2. 效果图:3. 代码3.1 封装组件代码3.2 父组件使用 1. 需求描述: 点击添加行,增加一级目录结构当类型为object or array时,点击右侧➕,增加子集点击右侧🚮&#x…...

精准对接促合作:飞讯受邀参加市工信局举办的企业供需对接会
2023年9月21日,由惠州市工业和信息化局主办的惠州市工业软件企业与制造业企业供需对接会成功举办,对接会旨在促进本地工业软件企业与制造业企业的紧密合作,推动数字化转型的深入发展。此次会议在市工业和信息化局16楼会议室举行,会…...

数学建模之遗传算法
文章目录 前言遗传算法算法思想生物的表示初始种群的生成下一代种群的产生适应度函数轮盘赌交配变异混合产生新种群 停止迭代的条件遗传算法在01背包中的应用01背包问题介绍01背包的其它解法01背包的遗传算法解法生物的表示初始种群的生成下一代种群的产生适应度函数轮盘赌交配…...

ISO9001认证常见的不符合项
今天,整理了一些关于ISO9001质量管理体系审核最常见的不合格项,以供大家参考。 一、质量管理体系 1、质量手册(标准条款4.2.2) (1)各部门执行的文件与手册的规定不一致。 (2)质量…...
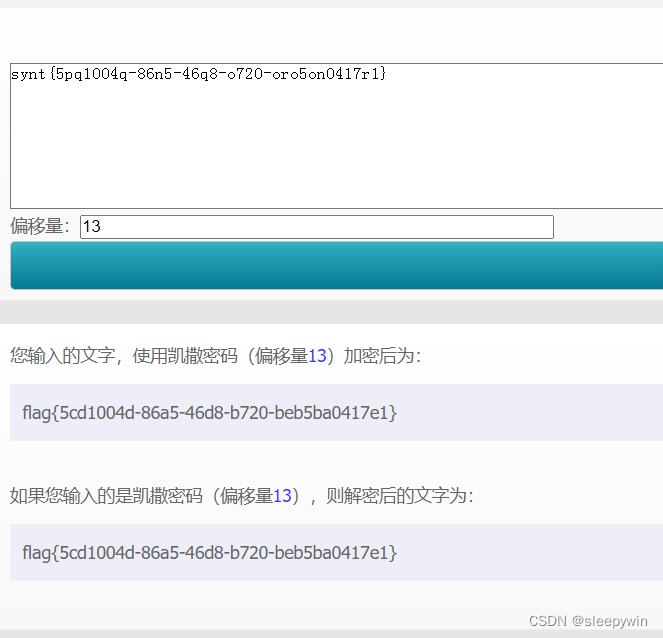
crypto:看我回旋踢
题目 下载压缩包后解压可得到提示文本 经过观察,synt{}这个提示与flag{}形式很像 由题目名中的回旋可以推测为凯撒密码,由凯撒密码的定义可知,需要先推出移位数,s->f数13次,因此移位数为13,解码可得...
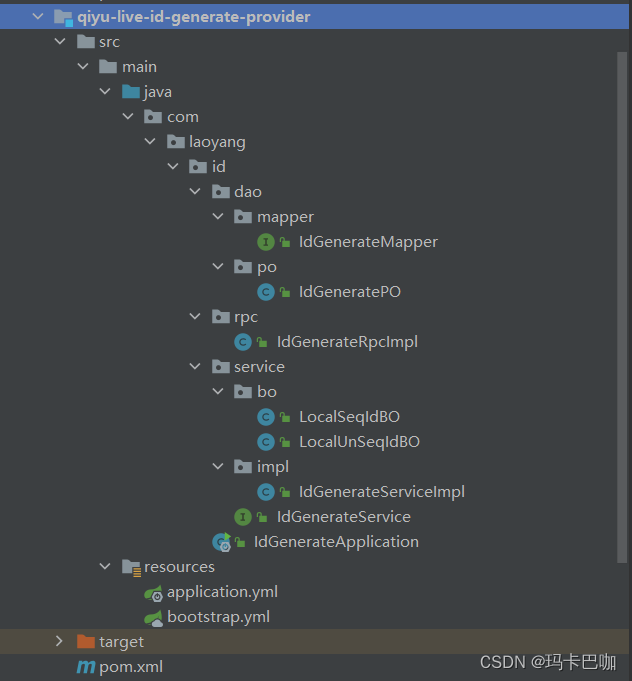
Springcloud实战之自研分布式id生成器
一,背景 日常开发中,我们需要对系统中的各种数据使用 ID 唯一表示,比如用户 ID 对应且仅对应一个人,商品 ID 对应且仅对应一件商品,订单 ID 对应且仅对应 一个订单。我们现实生活中也有各种 ID ,比如身…...
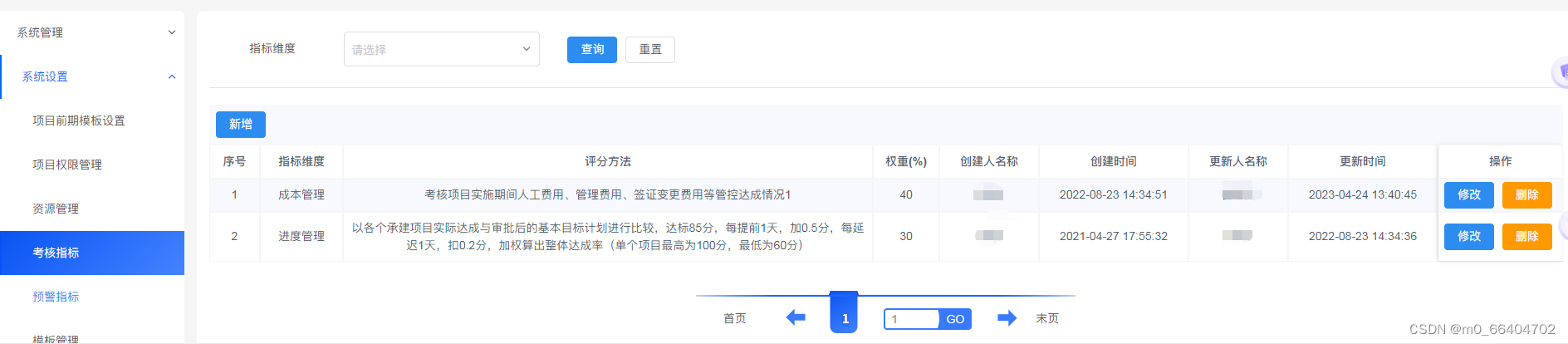
java 企业工程管理系统软件源码 自主研发 工程行业适用
工程项目管理软件(工程项目管理系统)对建设工程项目管理组织建设、项目策划决策、规划设计、施工建设到竣工交付、总结评估、运维运营,全过程、全方位的对项目进行综合管理 工程项目各模块及其功能点清单 一、系统管理 1、数据字典&am…...

Spring Cloud Alibaba Nacos 2.2.3 (4) - 本地源码编译 调试
下载nacos nacos在GitHub上有下载地址:https://github.com/alibaba/nacos/releases,可以选择任意版本下载。 我下载的是2.2.3 版本 导入idea mvn 安装包 1,切换到Terminal ,并且使用command prompt模式 2,执行 mvn -Prelease…...

WKB近似
WKB方法用于研究一种特定类型的微分方程的全局性质 很有用这种特定的微分方程形如: 经过一些不是特别复杂的推导,我们可以得到他的WKB近似解。 该近似解的选择取决于函数和参数的性质同时,我们默认函数的定义域为当恒大于零,时: 当…...
LeetCode算法二叉树—108. 将有序数组转换为二叉搜索树
目录 108. 将有序数组转换为二叉搜索树 代码: 运行结果: 给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。 高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不…...

如何设置 Git 短命令
设置 Git 短命令 对喜欢敲命令而不用图形化工具的爱好者来说,设置短命令可以很好的提高效率。下面介绍两种设置短命令的方式。 方式一 git config --global alias.ps push方式二 打开全局配置文件 vim ~/.gitconfig写入内容 [alias] co checkoutps pushpl p…...
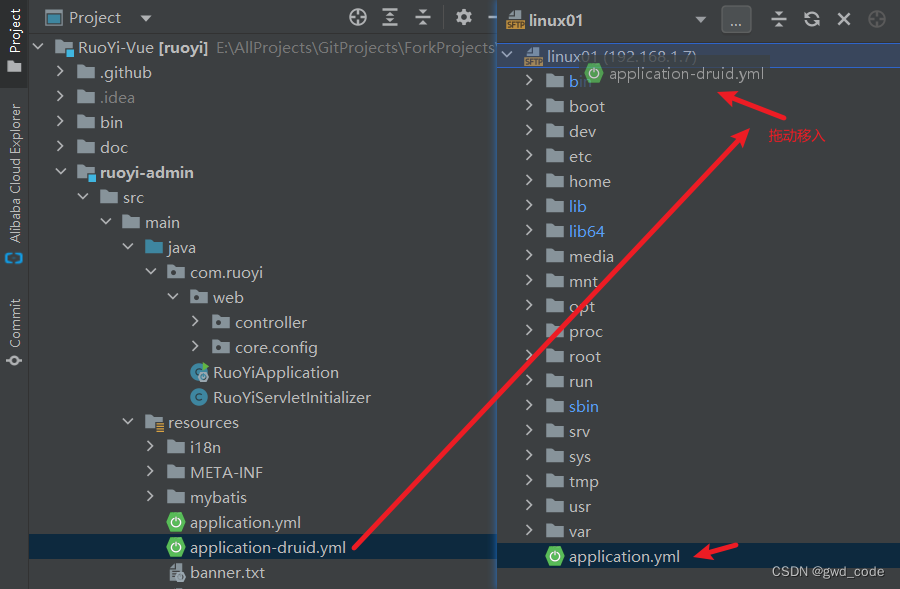
virtualbox无界面打开linux虚拟机的bat脚本,以及idea(代替Xshell)连接linux虚拟机的方法
virtualbox无界面打开linux虚拟机的bat脚本,以及idea连接linux虚拟机的方法 命令行运行代码成功运行的效果图 idea连接linux虚拟机的方法【重要】查看虚拟机的IP地址idea中选择菜单(该功能可代替Xshell软件)配置设置连接成功进入idea中的命令…...

mockito 的 InjectMocks 和 Mock 有什么区别?
InjectMocks 和 Mock 是 Mockito 框架中用于测试的注解,用于创建和管理模拟对象(mocks)的不同方式。它们有以下区别: InjectMocks: InjectMocks 用于注入模拟对象(mocks)到被测试对象…...

网络工程师的爬虫技术之路:跨界电商与游戏领域的探索
随着数字化时代的到来,跨界电商和游戏行业成为了网络工程师们充满机遇的领域。这两个领域都依赖于高度复杂的技术来实现商业目标和提供卓越的用户体验。本文将深入探讨网络工程师在跨界电商和游戏领域的技术挑战以及应对这些挑战的方法。 突破技术障碍的爬虫应用 …...
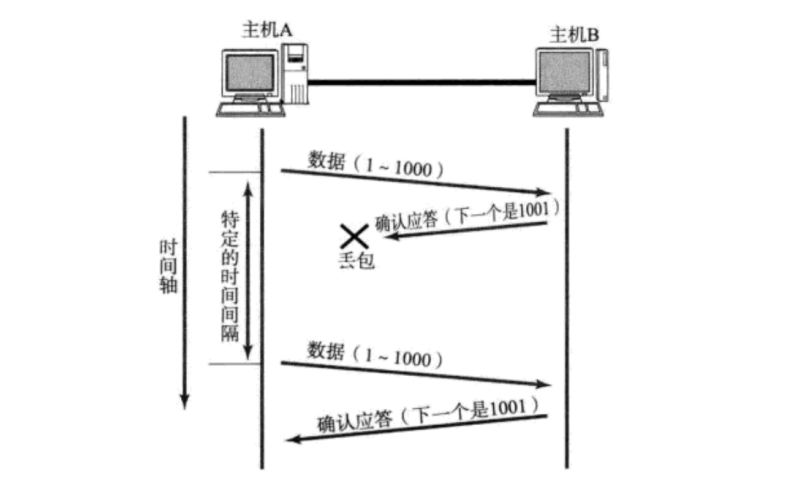
【TCP】确认应答 与 超时重传
确认应答 与 超时重传 一. 确认应答机制二. 超时重传机制 一. 确认应答机制 确认应答: 保障可靠传输的核心机制。 可靠传输: 不是指传输过去的数据不出错, 也不是指数据一定能传输过去,而是指发送方能够知道接收方是否接收到了数据。确认应答的关键就是接收方收到数…...

Kubernetes中Pod的扩缩容介绍
Kubernetes中Pod的扩缩容介绍 在实际生产系统中,我们经常会遇到某个服务需要扩容的场景,也可能会遇到由于资源紧张或者工作负载降低而需 要减少服务实例数量的场景。此时可以利用 Deployment/RC 的 Scale 机制来完成这些工作。 Kubernetes 对 Pod 的扩…...
vue点击pdf文件直接在浏览器中预览文件
好久没有更新文章了,说说为什么会有这篇文章呢,其实是应某个热线评论的要求出的,不过由于最近很长一段时间没打开csdn现在才看到,所以才会导致到现在才出。 先来看看封装完这个预览方法的使用,主打一个方便使用&#x…...

通讯网关软件012——利用CommGate X2OPC实现MS SQL数据写入OPC Server
本文推荐利用CommGate X2OPC实现从MS SQL服务器获取数据并写入OPC Server。CommGate X2OPC是宁波科安网信开发的网关软件,软件可以登录到网信智汇(http://wangxinzhihui.com)下载。 【案例】如下图所示,实现从MS SQL数据库获取数据并写入OPC Server。 【…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...
