WKB近似
- WKB方法用于研究一种特定类型的微分方程的全局性质
- 很有用
- 这种特定的微分方程形如:
- 经过一些不是特别复杂的推导,我们可以得到他的WKB近似解。
- 该近似解的选择取决于函数
和参数
的性质
- 同时,我们默认函数的定义域为
- 该近似解的选择取决于函数
- 当
恒大于零,
时:
- 当
恒小于零,
时:
- 注:很快你会发现两个问题
- a 和 b 是怎么确定的
- 答:初始条件
- \lambda 趋于正无穷 并不意味着 只有 \lambda 很大才能使得该WKB 近似真实
- a 和 b 是怎么确定的
- 当
存在一个或者多个零点时,函数的WKB近似会变得非常的复杂
- 我们一会再看
WKB 近似案例 1
- 该案例选取自参考文献【1】P137 例5.1.1
- 我们相信它的WKB近似为
- 我们使用四阶Runge-Kutta方法求解
import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import fsolveclass odessolver():def __init__(self, f, Y_start=np.array([0, 1]), dY_start=np.array([0, 0]), \X_start=0, X_end=1, h=0.01):self.f = fself.h = hself.X = np.arange(X_start, X_end, self.h)self.n = Y_start.sizeself.Y = np.zeros((self.n, self.X.size))#第一个参数表示元 第二个参数表示变量self.Y[:, 0] = Y_startself.Y[:, 1] = Y_start + self.h * dY_startself.tol = 1e-6def __str__(self):return f"y'(x) = f(x) = ({self.f}) variables"def RK4(self):for i in range(1, self.X.size):k1 = self.f(self.X[i-1] , self.Y[:, i-1])k2 = self.f(self.X[i-1] +self.h/2 , self.Y[:, i-1]+1/2*self.h*k1)k3 = self.f(self.X[i-1] +self.h/2 , self.Y[:, i-1]+1/2*self.h*k2)k4 = self.f(self.X[i-1] +self.h , self.Y[:, i-1]+ self.h*k3)self.Y[:, i] = self.Y[:, i-1] +self.h/6 * (k1 + 2*k2 + 2*k3 + k4)return self.Ydef IRK4(self):for i in range(1, self.X.size):def f1(k1, k2):f1_x = self.X[i-1] + self.h*(3-3**0.5)/6f1_y = self.Y[:, i-1]+k1/4*self.h+(3-2*3**0.5)/12*k2*self.hf1_res = self.f(f1_x, f1_y)return np.array([f1_res[i] for i in range(self.n)])def f2(k1, k2):f2_x = self.X[i-1] + self.h*(3+3**0.5)/6f2_y = self.Y[:, i-1]+k2/4*self.h+(3+2*3**0.5)/12*k1*self.hf2_res = self.f(f2_x, f2_y)return np.array([f2_res[i] for i in range(self.n)]) def func(k):k1 = np.array([k[i] for i in range(self.n)])k2 = np.array([k[i+self.n] for i in range(self.n)])doc = []for i in range(self.n):doc.append((k1 - f1(k1, k2))[i])for i in range(self.n):doc.append((k2 - f2(k1, k2))[i])return docsol = fsolve(func, np.zeros(self.n*2))self.Y[:, i] = self.Y[:, i-1] + 1/2 * self.h * (sol[:self.n] + sol[self.n:])return self.YA = 0
B = 1
Lambda = 1
Q = lambda x:(1+x**2)**2
Y0 = np.array([A, B])def test_fun(x, Y): return np.array([Y[1], Lambda**2 * Q(x) * Y[0]])c = odessolver(test_fun, Y_start=Y0)
x = np.arange(0, 1, 0.01)y3 = c.RK4()
x = np.arange(0, 1, 0.01)
plt.plot(x, y3[0, :], label="RK4")##y4 = c.IRK4()
##x = np.arange(0, 1, 0.01)
##plt.plot(x, y4[0, :], label="IRK4")WKB = lambda x:1/(Lambda*(1+x**2)**0.5)*(np.exp(x+x**3/3)-np.exp(-(x+x**3/3)))/2
plt.plot(x, WKB(x), label="WKB")plt.legend()
plt.pause(0.01)

- 看上去十分得合理
参考文献
[1]数学物理中的渐近方法 李家春 周显初 科学出版社
相关文章:

WKB近似
WKB方法用于研究一种特定类型的微分方程的全局性质 很有用这种特定的微分方程形如: 经过一些不是特别复杂的推导,我们可以得到他的WKB近似解。 该近似解的选择取决于函数和参数的性质同时,我们默认函数的定义域为当恒大于零,时: 当…...
LeetCode算法二叉树—108. 将有序数组转换为二叉搜索树
目录 108. 将有序数组转换为二叉搜索树 代码: 运行结果: 给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。 高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不…...

如何设置 Git 短命令
设置 Git 短命令 对喜欢敲命令而不用图形化工具的爱好者来说,设置短命令可以很好的提高效率。下面介绍两种设置短命令的方式。 方式一 git config --global alias.ps push方式二 打开全局配置文件 vim ~/.gitconfig写入内容 [alias] co checkoutps pushpl p…...
virtualbox无界面打开linux虚拟机的bat脚本,以及idea(代替Xshell)连接linux虚拟机的方法
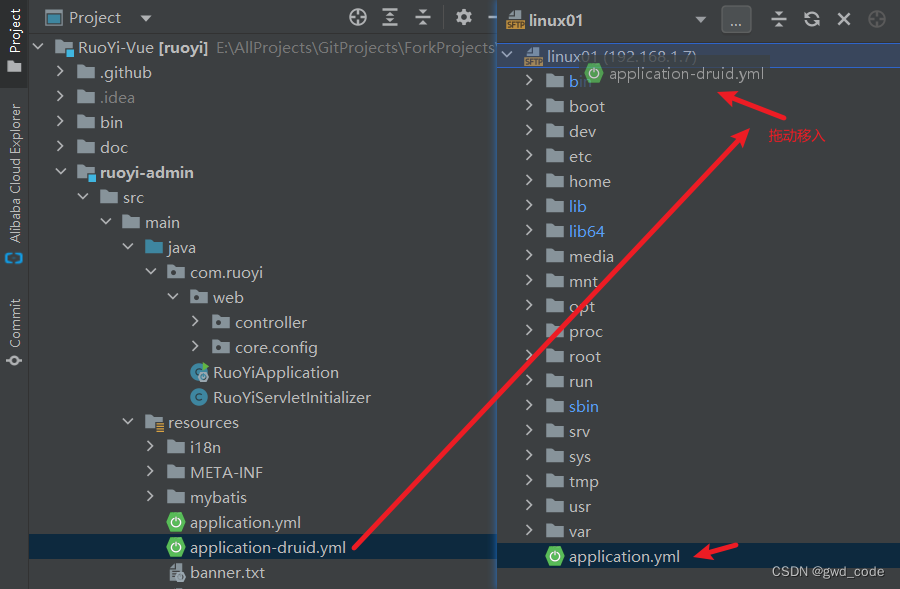
virtualbox无界面打开linux虚拟机的bat脚本,以及idea连接linux虚拟机的方法 命令行运行代码成功运行的效果图 idea连接linux虚拟机的方法【重要】查看虚拟机的IP地址idea中选择菜单(该功能可代替Xshell软件)配置设置连接成功进入idea中的命令…...

mockito 的 InjectMocks 和 Mock 有什么区别?
InjectMocks 和 Mock 是 Mockito 框架中用于测试的注解,用于创建和管理模拟对象(mocks)的不同方式。它们有以下区别: InjectMocks: InjectMocks 用于注入模拟对象(mocks)到被测试对象…...

网络工程师的爬虫技术之路:跨界电商与游戏领域的探索
随着数字化时代的到来,跨界电商和游戏行业成为了网络工程师们充满机遇的领域。这两个领域都依赖于高度复杂的技术来实现商业目标和提供卓越的用户体验。本文将深入探讨网络工程师在跨界电商和游戏领域的技术挑战以及应对这些挑战的方法。 突破技术障碍的爬虫应用 …...
【TCP】确认应答 与 超时重传
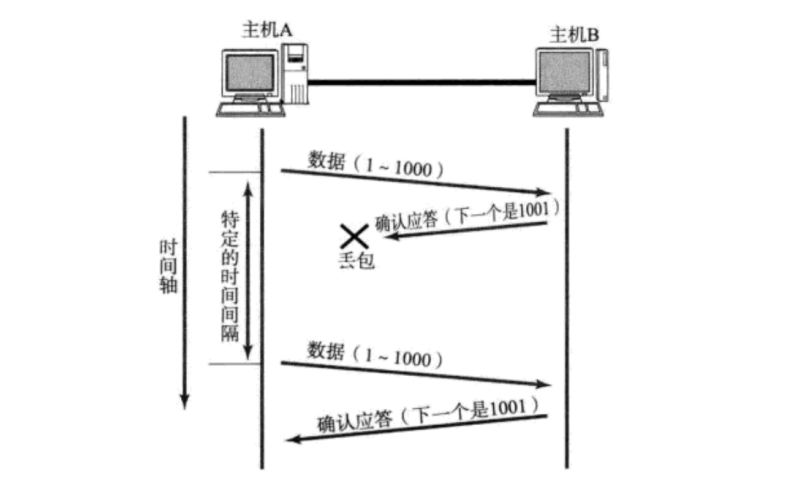
确认应答 与 超时重传 一. 确认应答机制二. 超时重传机制 一. 确认应答机制 确认应答: 保障可靠传输的核心机制。 可靠传输: 不是指传输过去的数据不出错, 也不是指数据一定能传输过去,而是指发送方能够知道接收方是否接收到了数据。确认应答的关键就是接收方收到数…...

Kubernetes中Pod的扩缩容介绍
Kubernetes中Pod的扩缩容介绍 在实际生产系统中,我们经常会遇到某个服务需要扩容的场景,也可能会遇到由于资源紧张或者工作负载降低而需 要减少服务实例数量的场景。此时可以利用 Deployment/RC 的 Scale 机制来完成这些工作。 Kubernetes 对 Pod 的扩…...
vue点击pdf文件直接在浏览器中预览文件
好久没有更新文章了,说说为什么会有这篇文章呢,其实是应某个热线评论的要求出的,不过由于最近很长一段时间没打开csdn现在才看到,所以才会导致到现在才出。 先来看看封装完这个预览方法的使用,主打一个方便使用&#x…...

通讯网关软件012——利用CommGate X2OPC实现MS SQL数据写入OPC Server
本文推荐利用CommGate X2OPC实现从MS SQL服务器获取数据并写入OPC Server。CommGate X2OPC是宁波科安网信开发的网关软件,软件可以登录到网信智汇(http://wangxinzhihui.com)下载。 【案例】如下图所示,实现从MS SQL数据库获取数据并写入OPC Server。 【…...
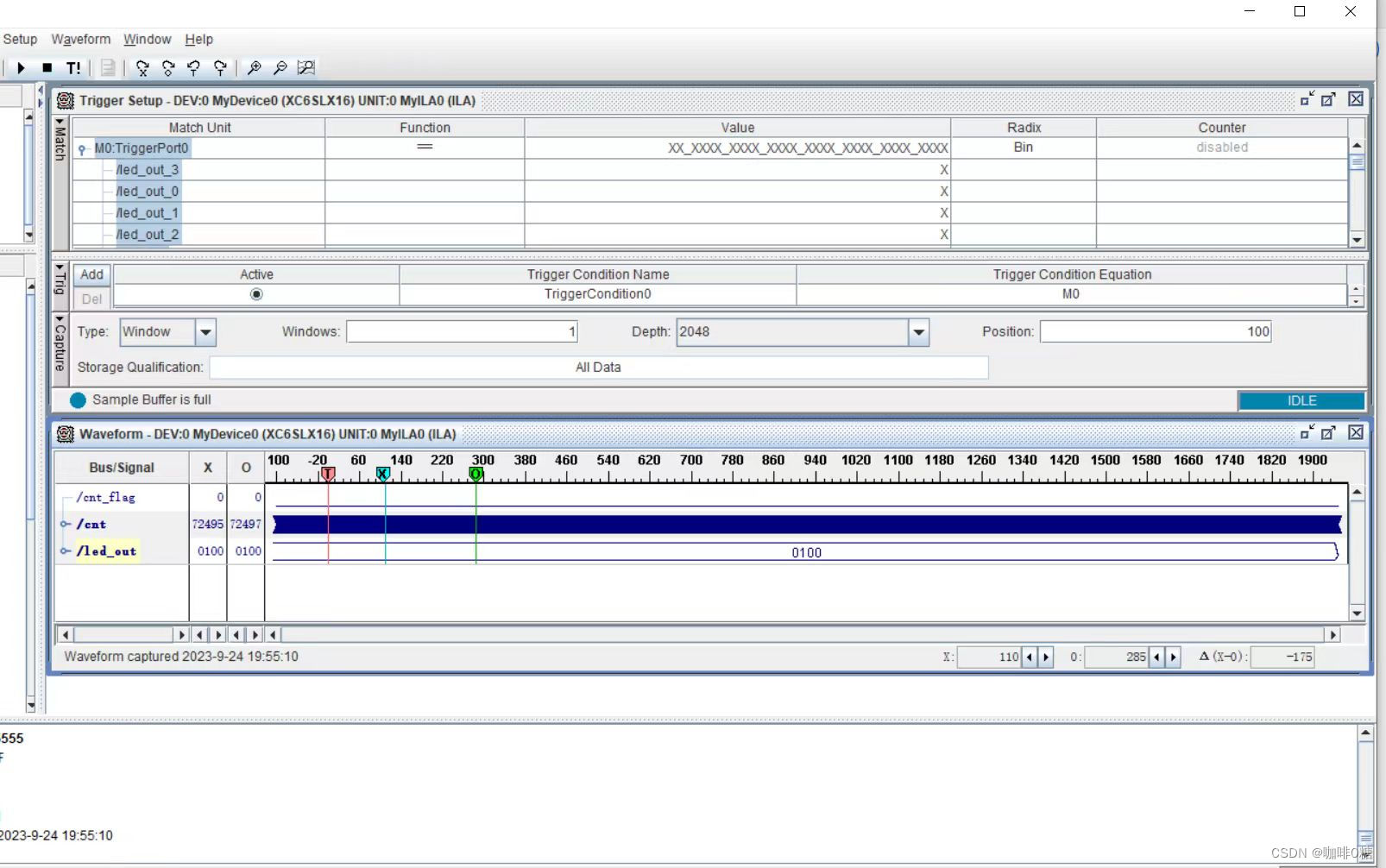
ISE_ChipScope Pro的使用
1.ChipScope Pro Core Inserter 使用流程 在之前以及编译好的流水灯实验上进行学习 ChipScope的使用。 一、新建一个ChipScope 核 点击Next,然后在下一个框中选择 Finish,你就会在项目菜单中看到有XX.cdc核文件。 二、对核文件进行设置 右键“Synthesize – XST” …...

北邮22级信通院数电:Verilog-FPGA(2)modelsim北邮信通专属下载、破解教程
北邮22信通一枚~ 跟随课程进度更新北邮信通院数字系统设计的笔记、代码和文章 持续关注作者 迎接数电实验学习~ 获取更多文章,请访问专栏: 北邮22级信通院数电实验_青山如墨雨如画的博客-CSDN博客 目录 1.下载 2.解压打开 3.modelsim初安装 4.…...
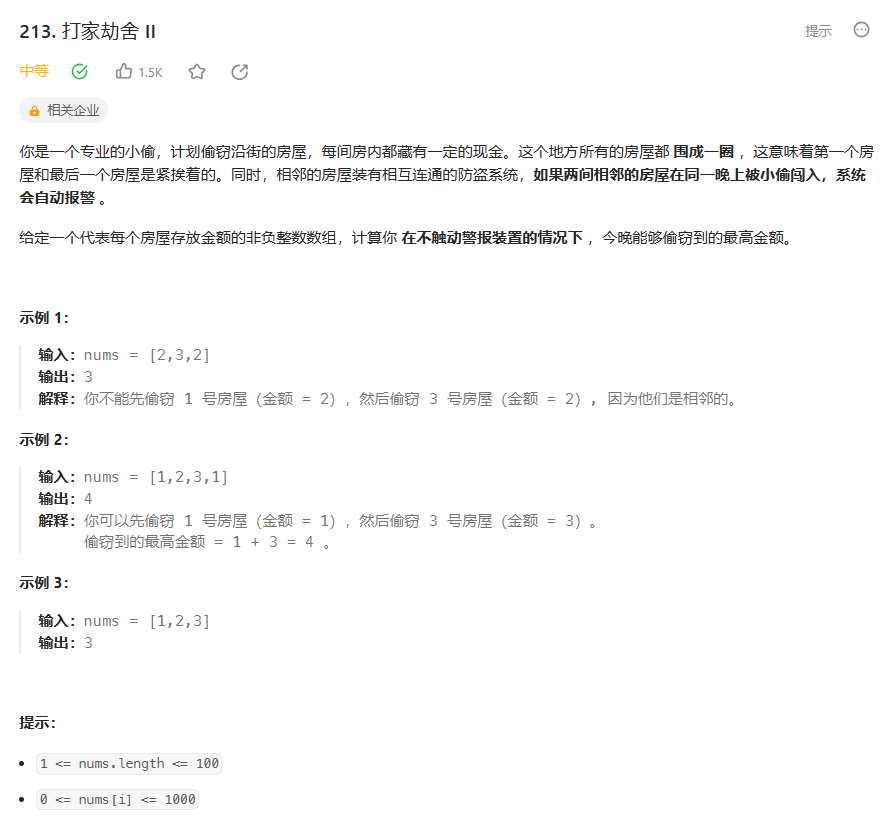
【力扣-每日一题】213. 打家劫舍 II
class Solution { public:int getMax(int n,vector<int> &nums){int a0,bnums[n],c0;for(int in1;i<nums.size()n-1;i){ //sizen-1,为0时,第一个可以偷,最后一个不能偷size-1;n为1时,最后一个可偷,计算…...
【PDF】pdf 学习之路
PDF 文件格式解析 https://www.cnblogs.com/theyangfan/p/17074647.html 权威的文档: 推荐第一个连接: PDF Explained (译作《PDF 解析》) | PDF-Explained《PDF 解析》https://zxyle.github.io/PDF-Explained/ https://zxyle…...

排序算法二 归并排序和快速排序
目录 归并排序 快速排序 1 挖坑法编辑 2 Hoare法 快排的优化 快排的非递归方法 七大排序算法复杂度及稳定性分析 归并排序 归并排序是建立在归并操作上的一种有效的排序算法,将以有序的子序列合并,得到完全有序的序列,即先使每个子序列有序,在使子序列段间有序.若将两…...

活动回顾 | 暴雨也无法阻挡的奔赴,2023 Meet TVM · 深圳站完美收官!
2023 Meet TVM 深圳站于 2023 年 9 月 16 日在腾讯大厦成功举办,百余名参与者亲临现场,聆听讲师们的精彩分享。 作者 | xixi 编辑 | 三羊 本文首发于 HyperAI 超神经微信公众平台~ **由 MLC.AI 社区和 HyperAI超神经主办,Openbayes贝式计算…...

JAVA_多线程的实现方式
线程的状态 方式一: public class Thread1 extends Thread {Overridepublic void run() {synchronized (this) {for (int i 0; i < 100; i) {System.out.println(getName() "" i);}}} } Thread1 thread1 new Thread1(); thread1.start(); 方式二…...
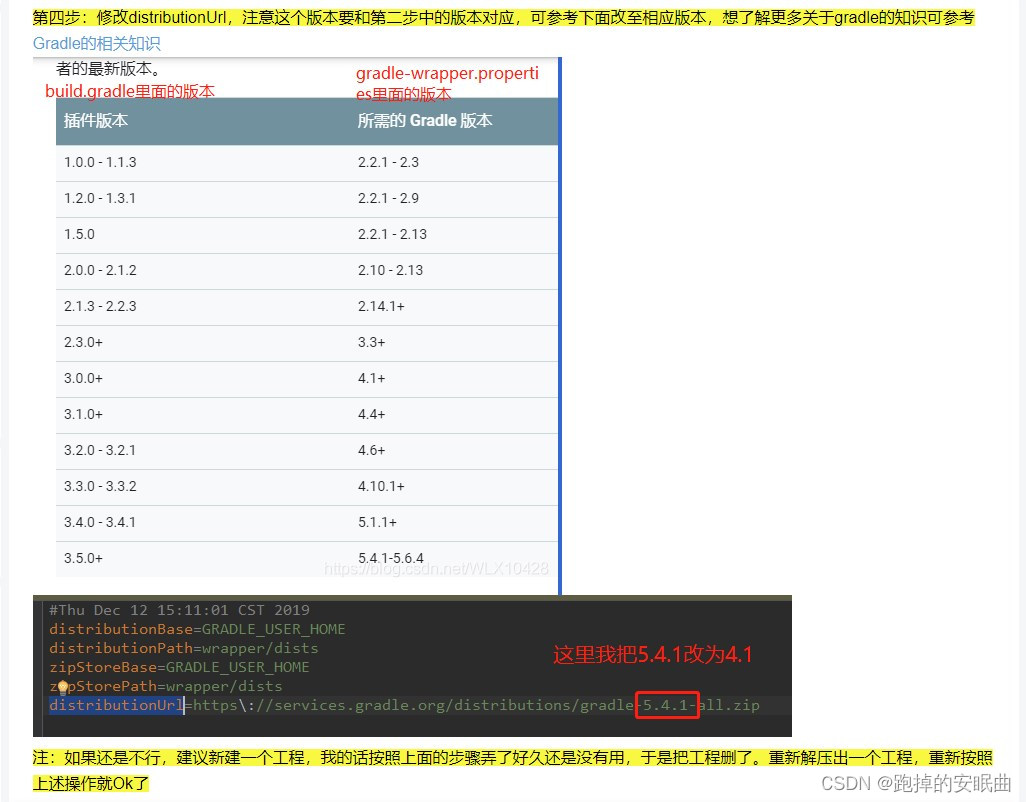
Android AndroidStudro版本gradle版本对应
详情网站:Android studio版本对用的gradle版本和插件版本(注意事项)...

Windows所有的端口及端口对应的程序
Windows所有的端口及端口对应的程序 1.查询Windows的端口 在CMD窗口运行: netstat -ano 结果示例: 活动连接协议 本地地址 外部地址 状态 PIDTCP 0.0.0.0:135 0.0.0.0:0 LISTENING 1156T…...
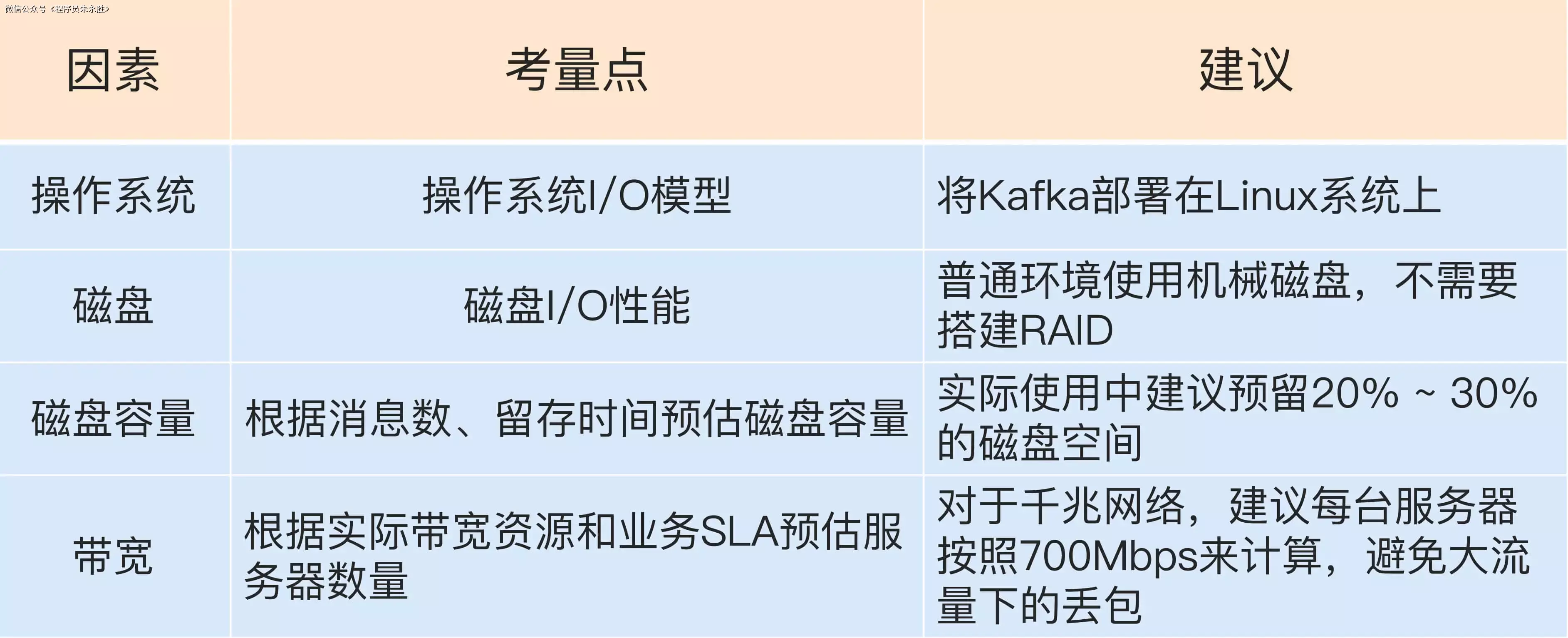
【Kafka系列】(二)Kafka的基本使用
有的时候博客内容会有变动,首发博客是最新的,其他博客地址可能会未同步,认准https://blog.zysicyj.top 首发博客地址[1] 文章更新计划[2] 系列文章地址[3] Kafka 线上集群部署方案怎么做 操作系统 先说结论,Kafka 部署在 Linux 上要比 Window…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...
