当前位置： 首页 > news >正文

【PDF】pdf 学习之路

news 2025/10/13 1:34:20

PDF 文件格式解析

https://www.cnblogs.com/theyangfan/p/17074647.html

权威的文档：

推荐第一个连接：

PDF Explained （译作《PDF 解析》） | PDF-Explained《PDF 解析》icon-default.png?t=N7T8https://zxyle.github.io/PDF-Explained/

https://zxyle.github.io/PDF-Explained/resources/pdf_reference_1.7.pdficon-default.png?t=N7T8https://zxyle.github.io/PDF-Explained/resources/pdf_reference_1.7.pdf

PDF Explained [Book]At last, here’s an approachable introduction to the widely used Portable Document Format. PDFs are everywhere, both online and in printed form, but few people take advantage of the useful … - Selection from PDF Explained [Book]icon-default.png?t=N7T8https://www.oreilly.com/library/view/pdf-explained/9781449321581/

相关文章：

【PDF】pdf 学习之路

PDF 文件格式解析 https://www.cnblogs.com/theyangfan/p/17074647.html 权威的文档： 推荐第一个连接： PDF Explained （译作《PDF 解析》） | PDF-Explained《PDF 解析》https://zxyle.github.io/PDF-Explained/ https://zxyle…...

编程日记 2023/9/26 0:30:31

排序算法二 归并排序和快速排序

目录 归并排序 快速排序 1 挖坑法​编辑 2 Hoare法 快排的优化 快排的非递归方法 七大排序算法复杂度及稳定性分析 归并排序 归并排序是建立在归并操作上的一种有效的排序算法,将以有序的子序列合并,得到完全有序的序列,即先使每个子序列有序,在使子序列段间有序.若将两…...

编程日记 2023/9/26 0:27:29

活动回顾 | 暴雨也无法阻挡的奔赴，2023 Meet TVM · 深圳站完美收官！

2023 Meet TVM 深圳站于 2023 年 9 月 16 日在腾讯大厦成功举办，百余名参与者亲临现场，聆听讲师们的精彩分享。 作者 | xixi 编辑 | 三羊 本文首发于 HyperAI 超神经微信公众平台~ **由 MLC.AI 社区和 HyperAI超神经主办，Openbayes贝式计算…...

编程日记 2023/9/26 0:26:28

JAVA_多线程的实现方式

线程的状态 方式一&#xff1a; public class Thread1 extends Thread {Overridepublic void run() {synchronized (this) {for (int i 0; i < 100; i) {System.out.println(getName() "" i);}}} } Thread1 thread1 new Thread1(); thread1.start(); 方式二…...

编程日记 2023/9/26 0:25:27

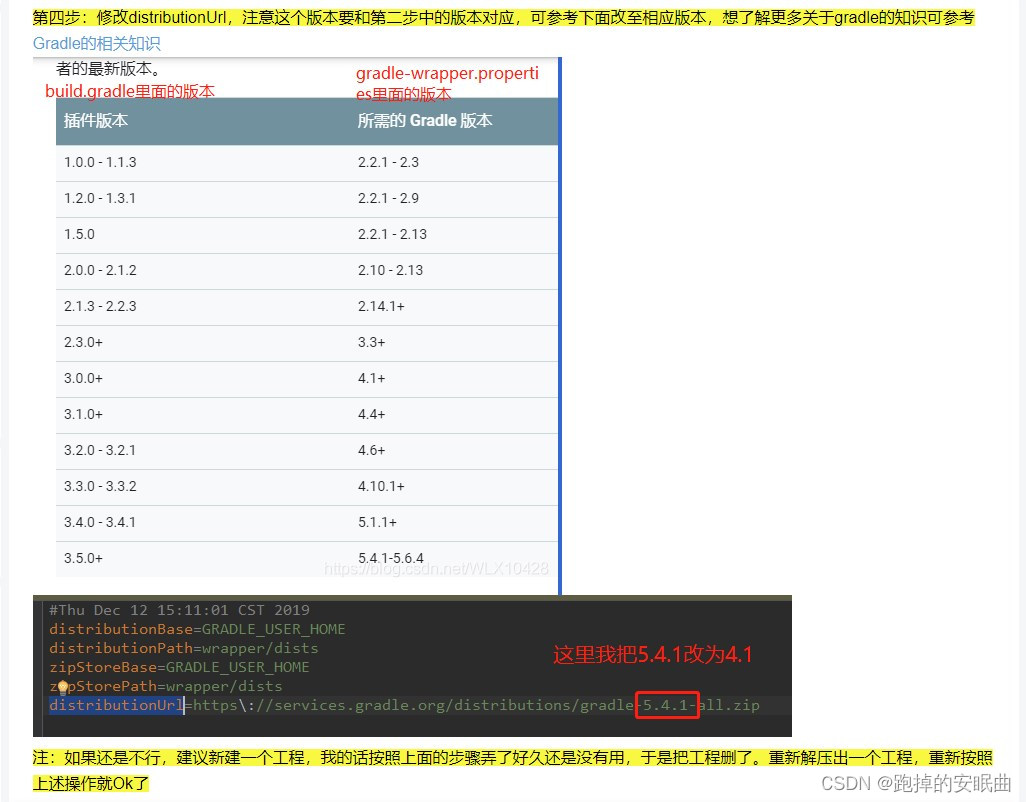
Android AndroidStudro版本gradle版本对应

详情网站&#xff1a;Android studio版本对用的gradle版本和插件版本&#xff08;注意事项&#xff09;...

编程日记 2023/9/26 0:24:25

Windows所有的端口及端口对应的程序

Windows所有的端口及端口对应的程序 1.查询Windows的端口 在CMD窗口运行&#xff1a; netstat -ano 结果示例&#xff1a; 活动连接协议 本地地址 外部地址 状态 PIDTCP 0.0.0.0:135 0.0.0.0:0 LISTENING 1156T…...

编程日记 2023/9/26 0:22:22

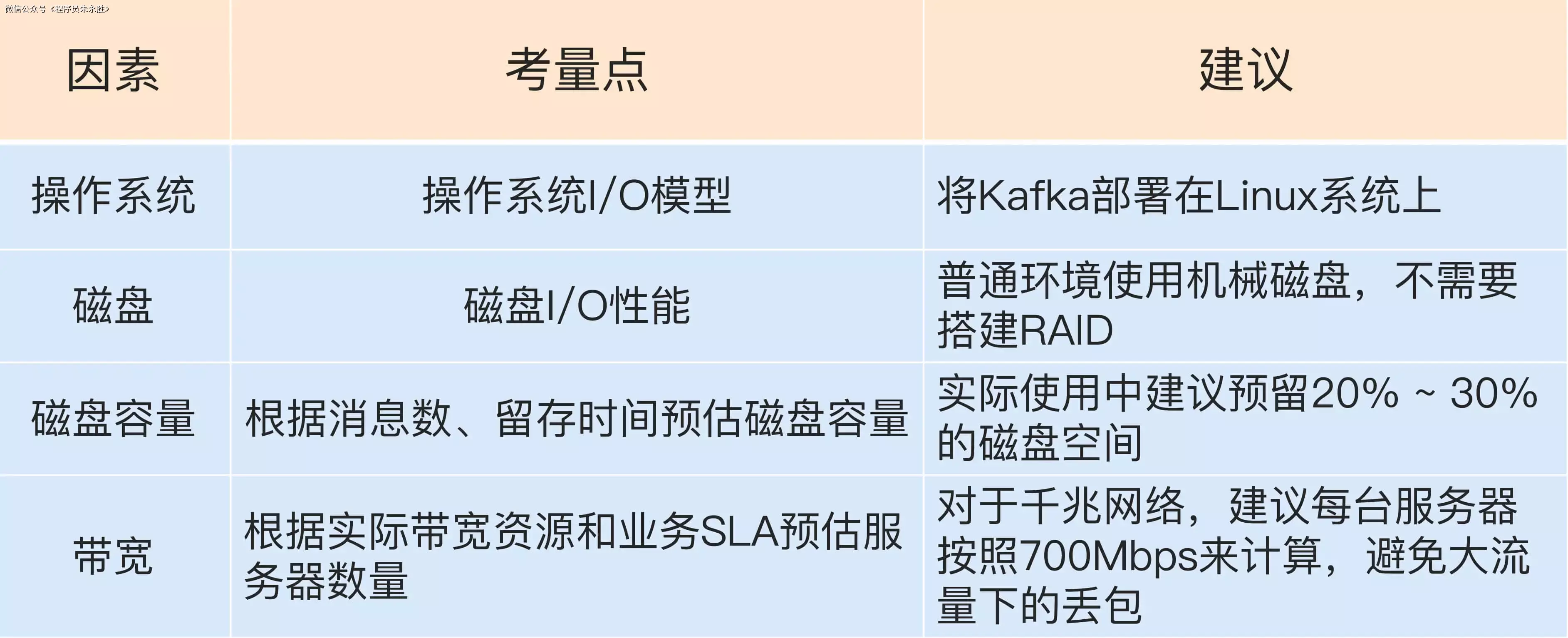
【Kafka系列】（二）Kafka的基本使用

有的时候博客内容会有变动&#xff0c;首发博客是最新的&#xff0c;其他博客地址可能会未同步,认准https://blog.zysicyj.top 首发博客地址[1] 文章更新计划[2] 系列文章地址[3] Kafka 线上集群部署方案怎么做 操作系统 先说结论&#xff0c;Kafka 部署在 Linux 上要比 Window…...

编程日记 2023/9/26 0:21:22

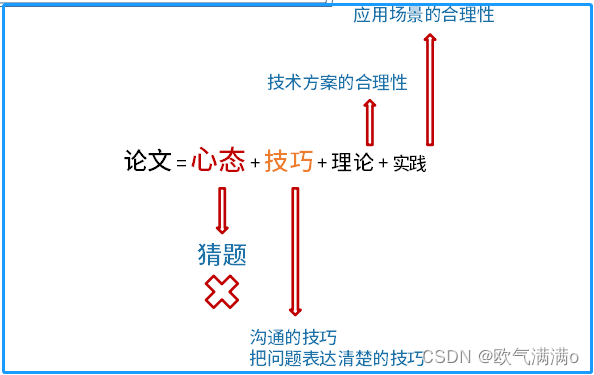
2023年下半年软考高级系统架构设计师论文指南（收藏）

由于今年下半年软考改为了机考&#xff0c;所以今年是看大家码字的速度了&#xff0c;但是好处还是有的&#xff0c;错了还能删除&#xff0c;之前纸质的 还有点不方便。 1、选择题目 &#xff08;1&#xff09;控制选题的时间。不要浪费太多时间在纠结选题上面。 &#xff…...

编程日记 2023/9/26 0:20:21

数据结构之【动态数组】

1. 线性表 概念&#xff1a;线性表是n个具有相同特性的数据元素的有限序列。 常见的线性表有&#xff1a;数组、链表、栈、队列、字符串…… 特点&#xff1a; 保存在这个结构中的元素都是相同的数据类型。元素之间线性排列&#xff0c;元素之间在逻辑上是连续的。 线性表…...

编程日记 2023/9/26 0:19:20

解答嵌入式和单片机的关系

嵌入式系统是一种特殊的计算机系统&#xff0c;用于特定任务或功能。而单片机则是嵌入式系统的核心部件之一&#xff0c;是一种在单个芯片上集成了处理器、内存、输入输出接口等功能的微控制器。刚刚好我这里有一套单片机保姆式教学&#xff0c;里面有编程教学、问题讲解、语言…...

编程日记 2023/9/26 0:16:18

利用Pycharm将python程序打包为exe文件（亲测可用）

最近做了一个关于py的小项目&#xff0c;对利用Pycharm将python文件打包为exe文件不是很熟悉&#xff0c;故学习记录之。 目录 一、下载pyinstaller库 二、打开Pycharm进行打包&#xff08;不更改图标&#xff09; 三、打开Pycharm进行打包&#xff08;更改图标&#xff09…...

编程日记 2023/9/26 0:13:14

解决Vue设置图片的动态src不生效的问题

一、问题描述 在vue项目中&#xff0c;想要动态设置img的src时&#xff0c;此时发现图片会加载失败。在Vue代码中是这样写的&#xff1a; 在Vue的data中是这样写的&#xff1a; 我的图片在根目录下的static里面&#xff1a; 但是在页面上这个图片却无法加载出来。 二、解决方案…...

编程日记 2023/9/26 0:11:13

企业关键数据采集如何做

数据对于企业的重要性不言而喻&#xff0c;目前又处于大数据时代&#xff0c;企业对于数据的解读将是辅助决策最重要的一环。依据所掌握的数据信息&#xff0c;帮助企业做决策的优化。然而&#xff0c;在企业的关键数据采集并不是一项简单轻松的任务&#xff0c;他需要企业投入…...

编程日记 2023/9/26 0:10:13

抖音SEO矩阵系统源码开发搭建

1. 确定需求和功能&#xff1a;明确系统的主要目标和需要实现的功能&#xff0c;包括关键词研究、短视频制作、外链建设、数据分析、账号设置优化等方面。 2. 设计系统架构&#xff1a;根据需求和功能确定系统的架构&#xff0c;包括前端、后端、数据库等部分的设计&#xff0…...

编程日记 2023/9/26 0:09:12

20230925工作心得

1、如果使用map的时候&#xff0c;担心key重复&#xff0c;覆盖掉值 那么直接加个if/else判断就好了。 如果map.containsKey&#xff0c;那么就把值追加上去&#xff0c;否则就直接put。 2、list的removeAll方法 list.removeAll(list2);//list要removeAll谁,就是看list自己比…...

编程日记 2023/9/26 0:08:09

ESP32在CAN(TWAI)波特率不同时收发数据，导致总线错误无法恢复

问题描述&#xff1a; 总线上有两个设备&#xff0c;主机&#xff1a;100ms周期发送数据。从机&#xff1a;以不同波特率发送数据&#xff0c;再把从机波特率调节至主机波特率一致无法通信。 环境&#xff1a;VSCODE IDF-v5.0 问题分析&#xff1a; 我们先看下ESP32技术参…...

编程日记 2023/9/26 0:07:08

精简版背包问题|01背包、完全背包、多重背包

背包问题 01背包问题 有n个物品&#xff0c;它们有各自的体积w和价值v&#xff0c;现有给定容量W的背包&#xff0c;在总体积不超过背包承载上限的情况下&#xff0c;如何让背包里装入的物品具有最大的价值总和&#xff1f;&#xff08;每个物品最多可使用一次&#xff09; w(…...

编程日记 2023/9/26 0:06:08

五、核支持向量机算法(NuSVC，Nu-Support Vector Classification)（有监督学习）

和支持向量分类(Nu-Support Vector Classification)&#xff0c;与 SVC 类似&#xff0c;但使用一个参数来控制支持向量的数量&#xff0c;其实现基于libsvm 一、算法思路 本质都是SVM中的一种优化&#xff0c;原理都类似&#xff0c;详细算法思路可以参考博文&#xff1a;三…...

编程日记 2023/9/26 0:05:07

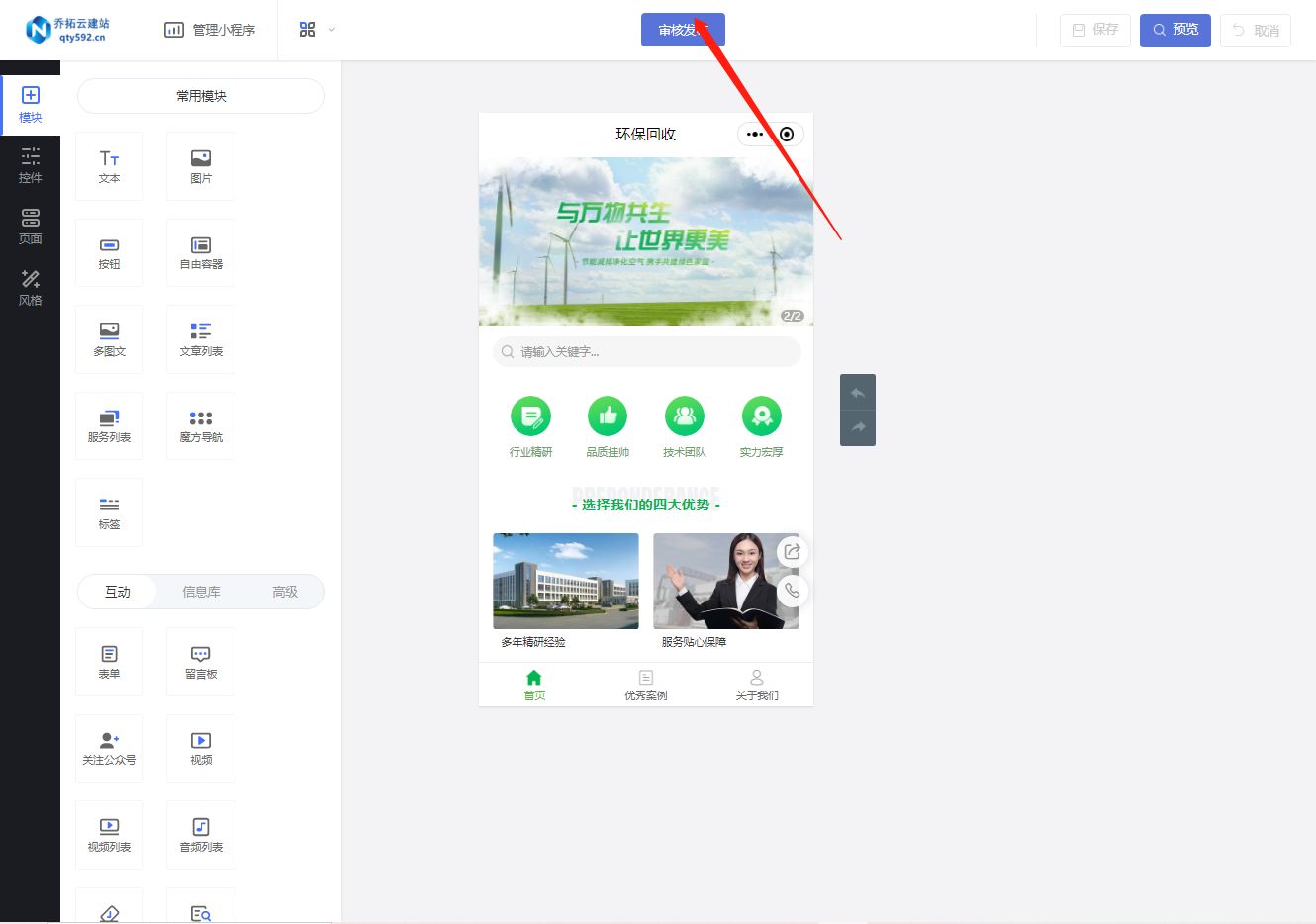
个人废品回收小程序制作步骤详解

在当今的环保时代&#xff0c;个人废品回收小程序的发展显得尤为重要。为了满足这一需求&#xff0c;本文将详细介绍如何制作一个个人废品回收小程序。 第一步&#xff0c;进入乔拓云网后台&#xff0c;点击【轻应用小程序】进入设计小程序页面。在这个页面&#xff0c;你可以看…...

编程日记 2023/9/26 0:04:06

Python爬虫自动切换爬虫ip的完美方案

在进行网络爬虫时&#xff0c;经常会遇到需要切换爬虫ip的情况&#xff0c;以绕过限制或保护自己的爬虫请求。今天&#xff0c;我将为你介绍Python爬虫中自动切换爬虫ip的终极方案&#xff0c;让你的爬虫更加高效稳定。 步骤一&#xff1a;准备爬虫ip池 首先&#xff0c;你需要…...

编程日记 2023/9/26 0:03:05

如何在看板中体现优先级变化

在看板中有效体现优先级变化的关键措施包括&#xff1a;采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中&#xff0c;设置任务排序规则尤其重要&#xff0c;因为它让看板视觉上直观地体…...

编程新知 2025/10/8 22:38:55

家政维修平台实战20：权限设计

目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系&#xff0c;主要是分成几个表&#xff0c;用户表我们是记录用户的基础信息&#xff0c;包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题&#xff0c;不同的角色&#xf…...

编程新知 2025/10/8 22:37:46

DBAPI如何优雅的获取单条数据

API如何优雅的获取单条数据 案例一 对于查询类API&#xff0c;查询的是单条数据&#xff0c;比如根据主键ID查询用户信息&#xff0c;sql如下&#xff1a; select id, name, age from user where id #{id}API默认返回的数据格式是多条的&#xff0c;如下&#xff1a; {&qu…...

编程新知 2025/10/6 5:34:30

数据库分批入库

今天在工作中&#xff0c;遇到一个问题&#xff0c;就是分批查询的时候&#xff0c;由于批次过大导致出现了一些问题&#xff0c;一下是问题描述和解决方案&#xff1a; 示例&#xff1a; // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

编程新知 2025/7/18 1:50:27

基于Java+MySQL实现（GUI）客户管理系统

客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息&#xff0c;对客户进行统一管理&#xff0c;可以把所有客户信息录入系统&#xff0c;进行维护和统计功能。可通过文件的方式保存相关录入数据&#xff0c;对…...

编程新知 2025/9/24 6:15:48

【JavaSE】多线程基础学习笔记

多线程基础 -线程相关概念 程序&#xff08;Program&#xff09; 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序&#xff0c;比如我们使用QQ&#xff0c;就启动了一个进程&#xff0c;操作系统就会为该进程分配内存…...

编程新知 2025/9/12 0:57:34

人工智能--安全大模型训练计划：基于Fine-tuning + LLM Agent

安全大模型训练计划&#xff1a;基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标&#xff1a;为安全大模型创建高质量、去偏、符合伦理的训练数据集&#xff0c;涵盖安全相关任务&#xff08;如有害内容检测、隐私保护、道德推理等&#xff09;。 1.1 数据收集 描…...

编程新知 2025/10/10 20:10:50

Linux系统部署KES

1、安装准备 1.版本说明V008R006C009B0014 V008&#xff1a;是version产品的大版本。 R006&#xff1a;是release产品特性版本。 C009&#xff1a;是通用版 B0014&#xff1a;是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存&#xff1a;1GB 以上 硬盘&#xf…...

编程新知 2025/8/16 12:41:25

Vue 模板语句的数据来源

&#x1f9e9; Vue 模板语句的数据来源&#xff1a;全方位解析 Vue 模板&#xff08;<template> 部分&#xff09;中的表达式、指令绑定&#xff08;如 v-bind, v-on&#xff09;和插值&#xff08;{{ }}&#xff09;都在一个特定的作用域内求值。这个作用域由当前 组件…...

编程新知 2025/10/4 11:36:04

mac：大模型系列测试

0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何&#xff0c;是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试&#xff0c;是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

编程新知 2025/10/11 4:46:28