精简版背包问题|01背包、完全背包、多重背包
背包问题
01背包问题
有n个物品,它们有各自的体积w和价值v,现有给定容量W的背包,在总体积不超过背包承载上限的情况下,如何让背包里装入的物品具有最大的价值总和?(每个物品最多可使用一次)
w(i) 表示第i个物品的体积,v(i) 表示第i个物品的价值,
dp[i,j] : 当前背包容量为j,前i个物品最佳组合对应的价值。
不装入第i个商品,则dp[i,j] = dp[i-1, j],
装入第i个商品, 则dp[i,j] = dp[i-1, j-w(i)] + v(i),
dp[i,j] = max{dp[i-1, j], dp[i-1, j-w(i)] + v(i)} j>=w(i).
完全背包问题
有n种物品和一个容量为W的背包,第i种物品的体积是w(i),价值是v(i)。在总体积不超过背包承载上限的情况下,求解将哪些物品装入背包,可使这些物品的总价值最大。(每种物品都有无限件可用)
从装入第i种物品多少件出发,01背包只有两种情况即取0件和取1件,而这里是取0件、1件、2件…直到超过限重(k>j/w(i))
dp[i][j] : 当前背包容量为j,前i个物品最佳组合对应的价值。
#k为装入第i种物品的件数,k<=j/w(i)
dp[i][j] = max{ (dp[i-1][j- kw(i)] + kv(i) ) for every k }
多重背包问题
有n种物品和一个容量为W的背包,第i种物品的数量为s(i),体积是w(i),价值是v(i)。在总体积不超过背包承载上限的情况下,求解将哪些物品装入背包,可使这些物品的总价值最大。(每种物品的数量有限制)
从装入第i种物品多少件出发,取0件、1件、2件…s(i)件,还要满足不超过限重。
dp[i][j]: 当前背包容量为j,前i个物品最佳组合对应的价值。
#k为装入第i种物品的件数,k<= min{ s(i), j/w(i)}
dp[i][j] = max{ (dp[i-1][j-kw(i)] + kv(i)) for every k}
胡乱的参考链接-_-||
https://blog.csdn.net/woomay/article/details/133162560?spm=1001.2014.3001.5501
https://blog.csdn.net/weixin_41082481/article/details/115922389?spm=1001.2101.3001.6650.1&utm_medium=distribute.pc_relevant.none-task-blog-2defaultBlogCommendFromBaiduRate-1-115922389-blog-72900009.235%5Ev38%5Epc_relevant_default_base3&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2defaultBlogCommendFromBaiduRate-1-115922389-blog-72900009.235%5Ev38%5Epc_relevant_default_base3&utm_relevant_index=2
动态规划-背包问题
https://blog.csdn.net/qq_37767455/article/details/99086678
https://zhuanlan.zhihu.com/p/93857890
https://blog.csdn.net/qq_38410730/article/details/81667885
【动态规划】01背包问题(通俗易懂,超基础讲解)
https://www.zhihu.com/question/23995189 什么是动态规划(Dynamic Programming)?动态规划的意义是什么?
https://www.cnblogs.com/mhpp/p/7700235.html 动态规划初探及什么是无后效性? (转)
https://www.zdaiot.com/DataStructureAlgorithm/40%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E7%90%86%E8%AE%BA%EF%BC%9A%E4%B8%80%E7%AF%87%E6%96%87%E7%AB%A0%E5%B8%A6%E4%BD%A0%E5%BD%BB%E5%BA%95%E6%90%9E%E6%87%82%E6%9C%80%E4%BC%98%E5%AD%90%E7%BB%93%E6%9E%84%E3%80%81%E6%97%A0%E5%90%8E%E6%95%88%E6%80%A7%E5%92%8C%E9%87%8D%E5%A4%8D%E5%AD%90%E9%97%AE%E9%A2%98/
0动态规划理论:一篇文章带你彻底搞懂最优子结构、无后效性和重复子问题
https://blog.csdn.net/qq_30137611/article/details/77655707 什么是无后效性?
https://juejin.cn/post/6951922898638471181
看一遍就理解:动态规划详解
https://houbb.github.io/2020/01/23/data-struct-learn-07-base-dp#%E6%9C%80%E5%B0%8F%E8%B7%AF%E5%BE%84%E4%B9%8B%E5%92%8C
五大基本算法之动态规划算法
https://zhuanlan.zhihu.com/p/368901684?utm_campaign=&utm_medium=social&utm_oi=740423421275422720&utm_psn=1689458562500431873&utm_source=zhihu
https://www.zhihu.com/question/484180920/answer/2574186966?utm_campaign=&utm_medium=social&utm_oi=740423421275422720&utm_psn=1689463449510371328&utm_source=zhihu
https://seramasumi.github.io/docs/Algorithms/mc-%E5%BE%AE%E8%AF%BE%E5%A0%82-%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98.html
https://programmercarl.com/%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80%E5%AE%8C%E5%85%A8%E8%83%8C%E5%8C%85.html#%E7%AE%97%E6%B3%95%E5%85%AC%E5%BC%80%E8%AF%BE
https://blog.csdn.net/qq_37767455/article/details/99086678
https://blog.csdn.net/Biteht/article/details/124298926?spm=1001.2014.3001.5501
数据结构与算法—算法篇之动态规划(一)
https://blog.csdn.net/chinawangfei/article/details/123585910?utm_medium=distribute.pc_relevant.none-task-blog-2defaultbaidujs_baidulandingword~default-0-123585910-blog-99086678.235v38pc_relevant_sort_base3&spm=1001.2101.3001.4242.1&utm_relevant_index=1
背包问题之0-1背包算法详解
https://blog.csdn.net/char_m/article/details/107112564?utm_medium=distribute.pc_relevant.none-task-blog-2defaultbaidujs_baidulandingword~default-13-107112564-blog-99086678.235v38pc_relevant_sort_base3&spm=1001.2101.3001.4242.8&utm_relevant_index=14
https://blog.csdn.net/mu399/article/details/7722810
动态规划之01背包问题(最易理解的讲解)
https://github.com/youngyangyang04/leetcode-master/blob/master/problems/%E8%83%8C%E5%8C%85%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%8001%E8%83%8C%E5%8C%85-1.md
https://zhuanlan.zhihu.com/p/93857890
动态规划之背包问题系列
https://blog.csdn.net/woshi250hua/article/details/7636866
【DP_背包专辑】【10.14最新更新】
https://blog.csdn.net/weixin_41082481/article/details/115922389?spm=1001.2101.3001.6650.1&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7ERate-1-115922389-blog-72900009.235%5Ev38%5Epc_relevant_default_base3&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7ERate-1-115922389-blog-72900009.235%5Ev38%5Epc_relevant_default_base3&utm_relevant_index=2
动态规划-背包问题
相关文章:

精简版背包问题|01背包、完全背包、多重背包
背包问题 01背包问题 有n个物品,它们有各自的体积w和价值v,现有给定容量W的背包,在总体积不超过背包承载上限的情况下,如何让背包里装入的物品具有最大的价值总和?(每个物品最多可使用一次) w(…...
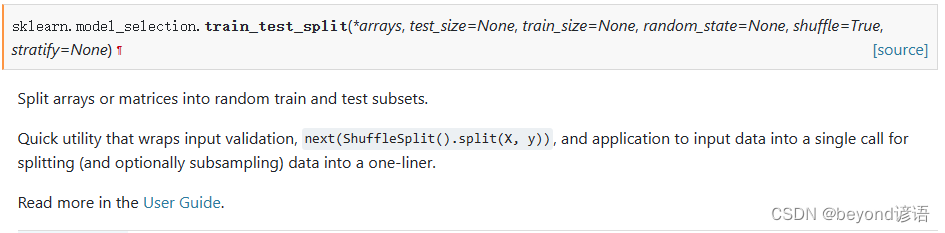
五、核支持向量机算法(NuSVC,Nu-Support Vector Classification)(有监督学习)
和支持向量分类(Nu-Support Vector Classification),与 SVC 类似,但使用一个参数来控制支持向量的数量,其实现基于libsvm 一、算法思路 本质都是SVM中的一种优化,原理都类似,详细算法思路可以参考博文:三…...
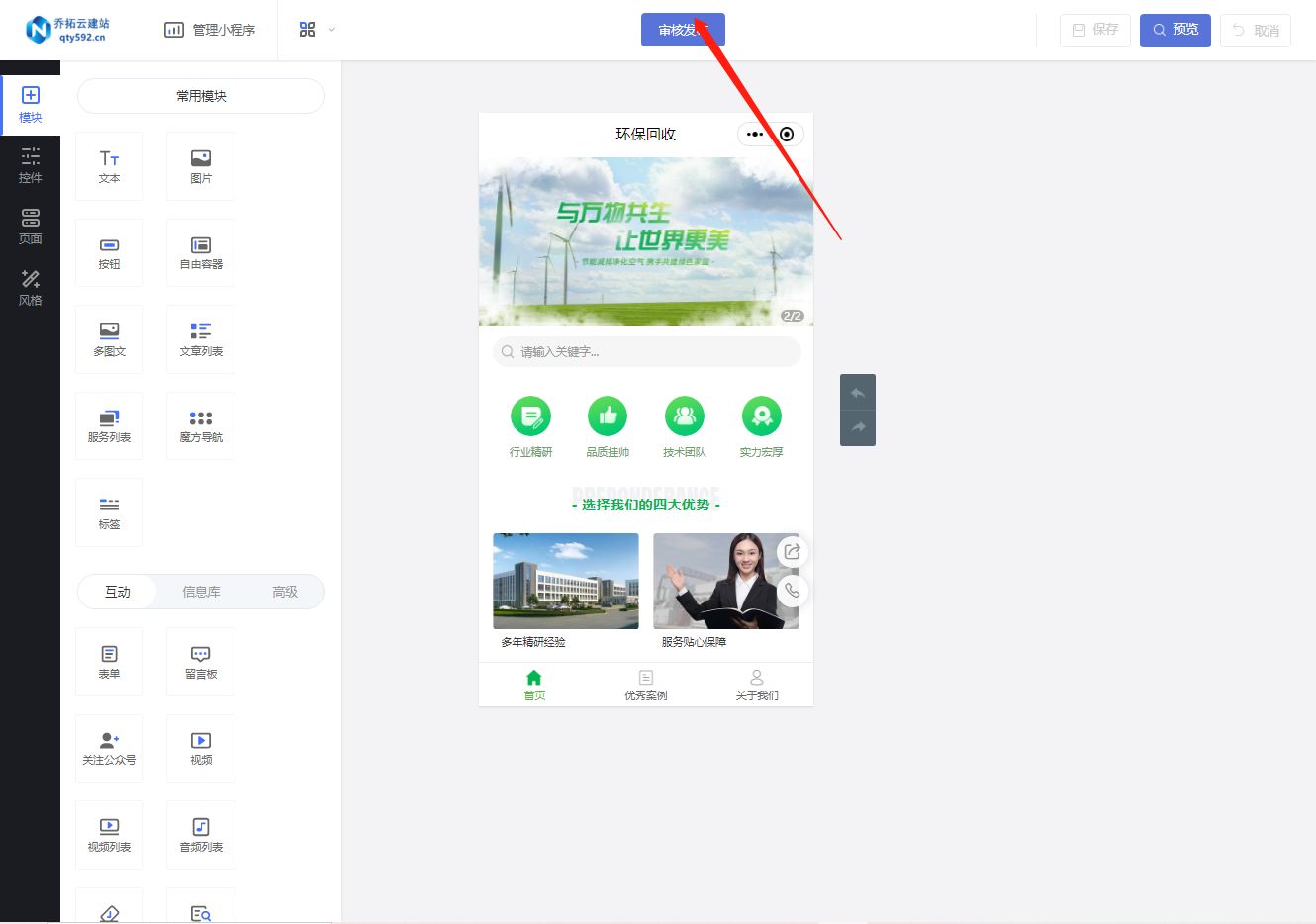
个人废品回收小程序制作步骤详解
在当今的环保时代,个人废品回收小程序的发展显得尤为重要。为了满足这一需求,本文将详细介绍如何制作一个个人废品回收小程序。 第一步,进入乔拓云网后台,点击【轻应用小程序】进入设计小程序页面。在这个页面,你可以看…...

Python爬虫自动切换爬虫ip的完美方案
在进行网络爬虫时,经常会遇到需要切换爬虫ip的情况,以绕过限制或保护自己的爬虫请求。今天,我将为你介绍Python爬虫中自动切换爬虫ip的终极方案,让你的爬虫更加高效稳定。 步骤一:准备爬虫ip池 首先,你需要…...
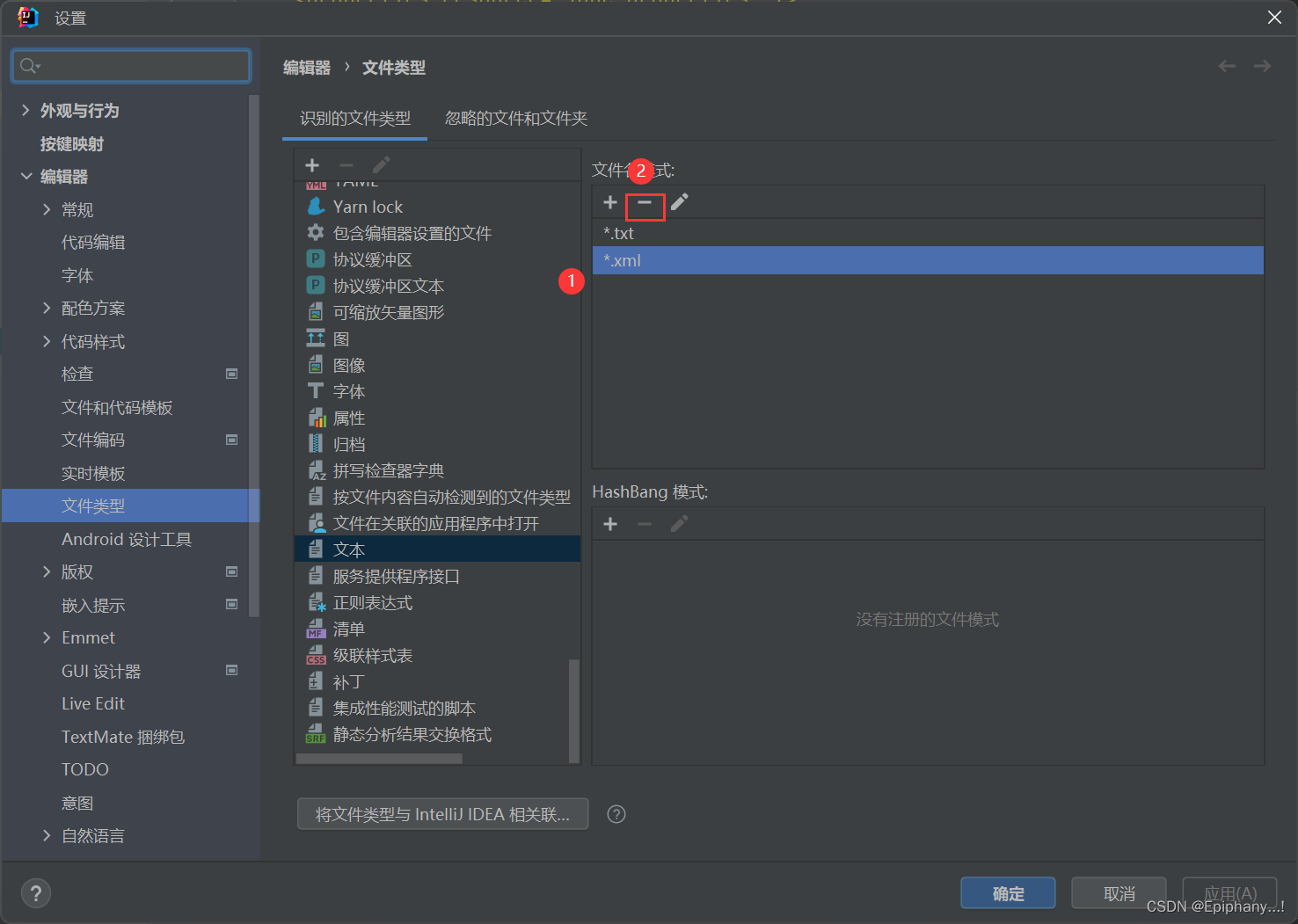
IDEA新建.xml文件显示为普通文本
情况如下: 1. 在XML文件中添加*.xml的文件名模式 2. 在文本中,选中*.xml进行删除...

linux的三剑客
1、grep命令 grep全称是Global Regular Expression Print,表示全局正则表达式版本,它的使用权限是所有用户。它是Linux系统中一种强大的文本搜索工具,它能使用正则表达式搜索文本,并把匹配的行打印出来。 shell脚本中也经常使用g…...

微信小程序部分知识点总结【2】
微信小程序的原理是什么 微信小程序的原理是基于一种轻量级的应用程序模型,它允许开发者在微信客户端内部创建和运行应用程序。微信小程序采用了类似网页的技术栈,主要由两部分组成:前端和后端。 前端部分使用HTML、CSS和JavaScript等标准的…...
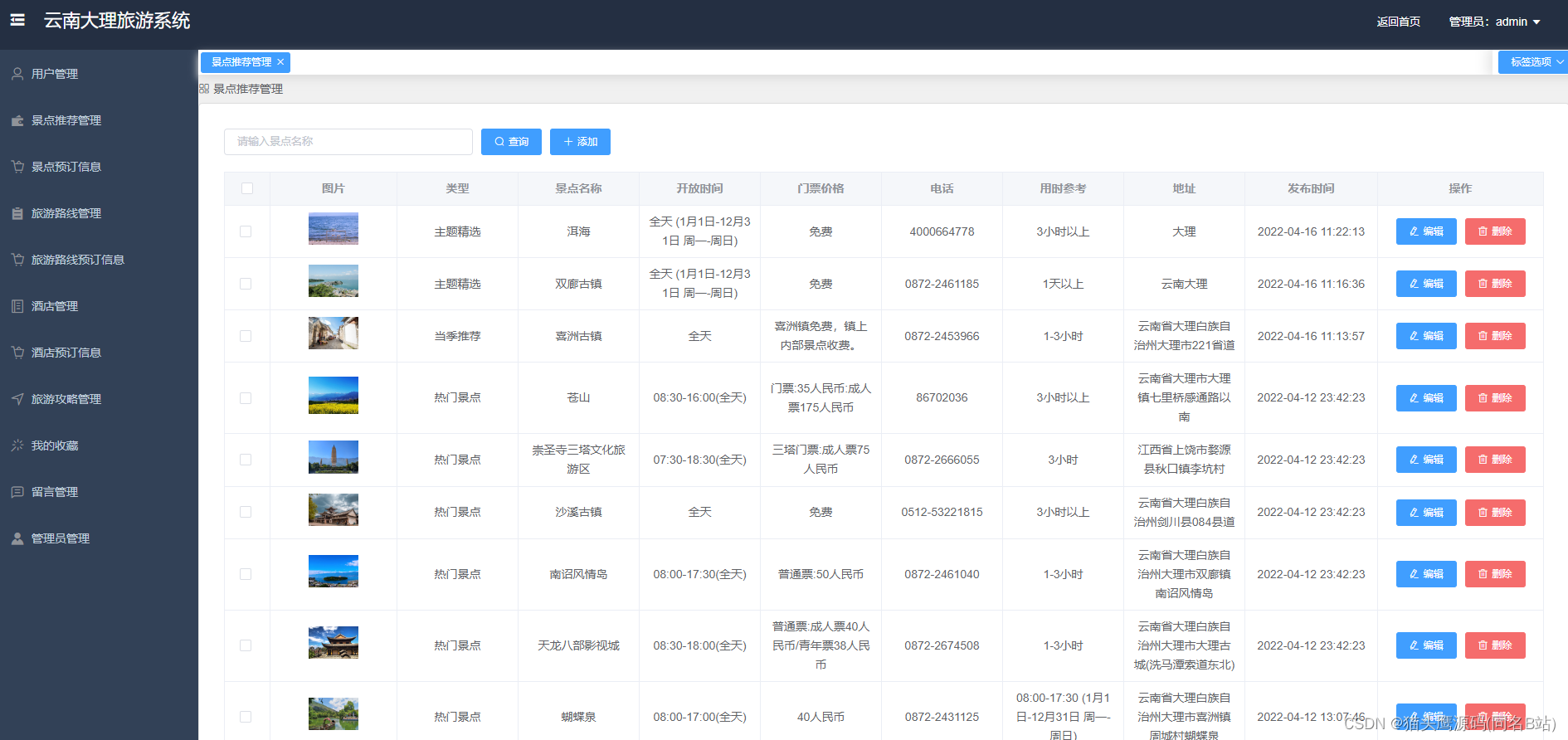
基于springboot+vue的云南旅游网(前后端分离)
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…...

后缀表达式求值
后缀表达式,又称逆波兰式,指的是不包含括号,运算符放在两个运算对象的后面,所有的计算按运算符出现的顺序,严格从左向右进行。 运用后缀表达式进行计算的具体做法: 建立一个操作数栈S。然后从左到右读表达…...
基于springboot+vue的信息技术知识赛系统
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…...
基于YOLOv8模型的垃圾满溢检测系统(PyTorch+Pyside6+YOLOv8模型)
摘要:基于YOLOv8模型的垃圾满溢检测系统可用于日常生活中检测与定位车辆垃圾(garbage)、垃圾桶(garbage_bin)和垃圾满溢(overflow)目标,利用深度学习算法可实现图片、视频、摄像头等…...

面试算法14:字符串中的变位词
题目 输入字符串s1和s2,如何判断字符串s2中是否包含字符串s1的某个变位词?如果字符串s2中包含字符串s1的某个变位词,则字符串s1至少有一个变位词是字符串s2的子字符串。假设两个字符串中只包含英文小写字母。例如,字符串s1为&quo…...

中国社科院大学-美国杜兰大学金融管理硕士暨能源管理硕士项目2023年毕业典礼
中国社科院大学-美国杜兰大学金融管理硕士暨能源管理硕士项目2023年毕业典礼 2023年9月16日,中国社会科学院大学-美国杜兰大学金融管理硕士项目暨能源管理硕士项目2023年毕业典礼在我校望京校区成功举办。 张波副校长致辞 中国社会科学院大学副校长张波教授、杜兰大…...

蓝桥杯 题库 简单 每日十题 day10
01 最少砝码 最少砝码 问题描述 你有一架天平。现在你要设计一套砝码,使得利用这些砝码 可以出任意小于等于N的正整数重量。那么这套砝码最少需要包含多少个砝码? 注意砝码可以放在天平两边。 输入格式 输入包含一个正整数N。 输出格式 输出一个整数代表…...
聊聊并发编程——多线程之synchronized
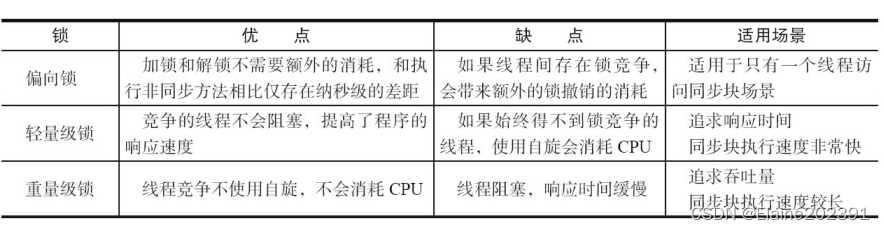
目录 一.多线程下数据不一致问题 二.锁和synchronized 2.1 并发编程三大特性 2.2引入锁概念 三.synchronized的锁实现原理 3.1 monitorenter和monitorexit 3.2synchronized 锁的升级 3.2.1偏向锁的获取和撤销 3.2.2轻量级锁的加锁和解锁 自适应自旋锁 轻量级锁的解锁…...

CompletableFuture-通用异步编程
演示Completable接口完全可以代替Future接口: CompletableFuture减少阻塞和轮询,可以传入回调对象,当异步任务完成或者发生异常时,自动 调用回调对象的回调方法。 package com.nanjing.gulimall.zhouyimo.test;import java.util…...
Vue3 封装 element-plus 图标选择器
一、实现效果 二、实现步骤 2.1. 全局注册 icon 组件 // main.ts import App from ./App.vue; import { createApp } from vue; import * as ElementPlusIconsVue from element-plus/icons-vueconst app createApp(App);// 全局挂载和注册 element-plus 的所有 icon app.con…...

超详细C语言实现——通讯录
目录 一、介绍 二、源代码 test.c: Contact.c: Contact.h: 代码运行结果: 三、开始实现 1.基本框架: 2.添加联系人: 3.显示联系人信息: 4.删除联系人信息: 5.查看指定联系人信息: 6.修改联系人…...

zabbix监控添加监控项及其监控Mysql、nginx
本届主要介绍添加监控项和修改中文乱码,监控mysql,nginx服务 一、zabbix监控添加监控项 1、配置agent服务器 在配置文件中添加: UserParameterlsq_userd,free -m | grep Mem | awk { print $3 } 服务器内存使用量 UserParameterdu,…...

Docker 部署 MongoDB 服务
拉取最新版本的 MongoDB 镜像: $ sudo docker pull mongo:latest在本地预先创建好 db 和 configdb 目录, 用于映射 MongoDB 容器内的 /data/db 和 /data/configdb 目录。 使用以下命令来运行 MongoDB 容器: $ sudo docker run -itd --name mongo --privilegedtru…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...
