【算法深入浅出】字符串匹配之 KMP 算法
KMP 算法是一种字符串匹配算法。字符串匹配算法的目标是:在字符串 s 中找到与模式串 p 相等的子串,输出其位置。例如:s = “abcdef”,p = “cdef”,p 在 s 中的位置是 2(从 0 开始计数)。

容易想到的方式就是暴力算法。
int findString(string s, string p) {int n = s.size(), m = p.size();int i, j;for (i = 0; i < n - m + 1; i++) {for (j = 0; j < m; j++) {if (s[i] == s[j]) continue;break;}if (j == m) return i;}return -1;}
暴力算法的最坏情况下,时间复杂度是 O ( n m ) O(nm) O(nm)。而本文尝试要讲明白的 kmp 算法,他的摊还时间复杂度是 O ( n ) O(n) O(n) 的。
kmp 算法执行速度要快不少,但是也是有代价的:也就是出了名的难理解。但我认为,只要 提纲挈领的找到 kmp 算法的主干,那还是比较好理解的,也就 2 分钟的事吧。算法实现上会有一些坑,这才是最难的地方,需要将里面的思路捋顺,但花些时间总能搞出来。那我们就开始吧。
从直觉开始
假设有这样一个样例:s = “bacbababababcbab”,p = “ababaca”。算法运行到如下位置时,匹配错误了。

暴力算法会移进 1 字符,然后重新从 s 的 5 号字符和 p 的 0 号字符开始匹配。相当于 s 的索引回退到 5,p 的索引回退到 0。

而 kmp 算法就比较聪明一些。既然 p 字符串的 0 到 4 号元素都匹配成功了,我们何不利用这个信息,多向前移动几个字符呢?怎么做呢? kmp 算法的思想如下:到目前位置,已经成功匹配了 p 的前缀中 “ababa” 这个字符串。然后我们同时考虑它的 前缀 和 后缀,会发现

它的前三个字符和后三个字符是完全一样的。所以我们完全可以向下图一样,从 s 的 9 号 字符和 p 的 3 号字符开始匹配,相当于 s 的索引没有回退,p 的索引回退到 3。这可比暴力匹配回退的少多了,因此也就快多了。
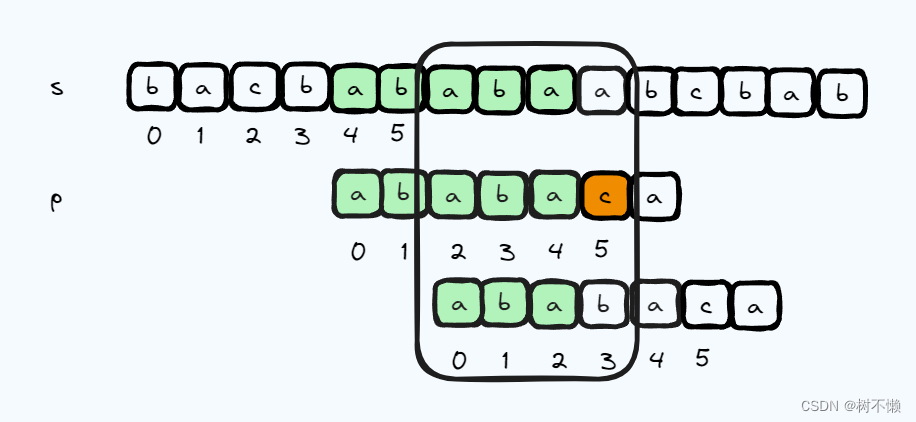
至此 kmp 算法的思想就讲完了。上述思想,如果不考虑如何实现的话,可能最多 2 分钟就可以理解。
但是想要实现它却又不知该怎么下手,那我们就一点一点的拆解它。
next 数组引入
next 数组,往往又叫前缀函数。我们不整那么高深的东西,就为了解决一个问题:p 的索引该回退到哪? 根据上面的分析,s 的索引是没有回退的,那么 p 的索引该回退到哪里呢?这个问题需要再精确一些:如果 p 在 索引 i 的位置匹配失败了,那么 p 的索引该回退到哪里?这就是 next 数组的作用:索引应该回退到 next[i] 的位置。
为了不使代码复杂化,我们先假设,如果已经得到了 next 数组,算法框架是什么样的呢?
- 版本1:
int findString(string s, string p) {int n = s.size(), m = p.size();int i, j = 0;for (i = 0; i < n;) {if (s[i] == p[j]) { // 如果相等,i 和 j 都进 1i++, j++;} else { // 如果不相等,i 保持不变,j 变为 next[j]j = next[j];}// 如果 j == m 表示 s 在 i 处匹配完成了,返回 i - m;if (j == m) return i - m;}return -1;}
根据版本一的注释,看起来好像没什么问题,但不幸的是,它有 bug。j = next[j] 这一行没有处理边界情况:即当s[i] 不等于 s[j],并且,当 j == 0 时,意味着 0 号位置也匹配失败了,这时候 next[j] 应该等于多少呢?答案是:还是 0。为什么呢?即使 0 号位置匹配失败了,下一次应该是要把 s 的索引加 1,而 p 的索引依旧是 0 才对。于是有了下面的代码版本。
plus. 有一些别的 kmp 算法版本 定义为 -1。实际上是把整个 next 数组做了一次变换,只要改一下 next 数组的定义即可。我们学会一个就好了。
版本2.1
int findString(string s, string p) {int n = s.size(), m = p.size();int i, j = 0, flag = 0;for (i = 0; i < n;) {if (s[i] == p[j]) { // 如果相等,i 和 j 都进 1i++, j++;} else { // 如果不相等,i 保持不变,j 变为 next[j]j = next[j];if (flag == 1) {flag = 0;i++;} else if (j == 0) flag = 1;}// 如果 j == m 表示 s 在 i 处匹配完成了,返回 i - m + 1;if (j == m) return i - m;}return -1;}
版本2.1是一个正确的版本,但是不够优雅。作为一个程序员,要有一定的审美,版本 2.1 本质上是用单层循环模拟了多层循环,如果能够拆出来,就更好了。
版本2.2
int n = s.size(), m = p.size();int i, j = 0;for (i = 0; i < n; i++) {// 如果不相等,i 保持不变,j 变为 next[j]while (j != 0 && s[i] != p[j]) {j = next[j];}if (s[i] == p[j]) { // 如果相等,j 进 1j++;}// 如果 j == m 表示 s 在 i 处匹配完成了,返回 i - m + 1;if (j == m) return i - m + 1;}return -1;}
嗯,版本2.2 就优雅许多了。
next 数组生成
那么 next 数组该如何生成呢?

对照这幅图,当 p 的 5 号索引匹配失败是,j 应该跳转到 3 号。可以观察到,next[i] 表示 [0, i - 1] 区间表示的字符串 p i p_i pi 中 重叠的前缀与后缀的最长值 k,并且 k 要小于 p i p_i pi 的长度,因为自己等于自己可不算。
所以算法如下
vector<int> next(m, 0);for (int i = 2; i < m; i++) { // 前两个数字默认为 0int t = next[i - 1]; // 前面的前面的那个区间有最长多少个重叠的前后缀// 前面的区间末尾 和 前面的前面的区间的末尾如果不相等就一直 next// 这点和匹配算法很像while (t != 0 && p[i - 1] != p[t]) { t = next[t];}next[i] = t;if (p[i - 1] == p[t]) next[i] = t + 1; //如果相等就 +1}
合成如下
int strStr(string s, string p) {int n = s.size(), m = p.size();// 求 next 数组vector<int> next(m, 0);for (int i = 2; i < m; i++) {int t = next[i - 1];while (p[i - 1] != p[t] && t != 0) t = next[t];if (p[i - 1] == p[t]) t++;next[i] = t;}// 匹配int j = 0;for (int i = 0; i < n; i++) {while (s[i] != p[j] && j != 0) j = next[j];if (s[i] == p[j]) j++;if (j == m) return i - m + 1;}return -1;}
总结
kmp 算法思想就是使用已匹配的前缀字符串,从中抽取出前后缀的重叠部分信息,用以减少字符串匹配中的回退,从而达到加速的作用。其实现有两个坑,一个是next 数组含义的准确定义(我的定义应该和书上不一样),第二个坑就是使用内循环来多次使用 next 数组跳转。其中第二个坑相信大家自己写都能意识到,第一个坑才是决定你能不能写出来的关键因素。我的实现可能不是最好的,但是希望能够好懂一点。
kmp 算法已将前缀信息使用到了极致,还有一些别的字符串比较算法要比 kmp 容易一些,比如 sunday 算法等。还有一些算法可能比 kmp 还要复杂一些,使用到了后缀信息,例如:bm 算法。还有 一个 RK 算法使用哈希字符串的方式,简单易写。这些算法有机会再说吧。
相关文章:

【算法深入浅出】字符串匹配之 KMP 算法
KMP 算法是一种字符串匹配算法。字符串匹配算法的目标是:在字符串 s 中找到与模式串 p 相等的子串,输出其位置。例如:s “abcdef”,p “cdef”,p 在 s 中的位置是 2(从 0 开始计数)。 容易想到…...

放弃webstrom转战vscode
本来是webstrom的忠实用户,无奈webstrom要么需要在网上找一个破解版或者不断的去找激活码,且破解版和激活码的文章总是很多,但是要找到真正有效的却总是要花费不少功夫。终于忍无可忍,转战vscode。(注:文中…...

VSCode 和 CLion
文章目录 一、VSCode1、文档2、插件3、智能编写4、VSCode 与 C(1)安装(2)调试(a)使用 CMake 进行跨平台编译与调试(b)launch.json(c)传参 (3&…...

Learn Prompt- Midjourney Prompt:Prompt 提示语
基础结构 一个基本的提示可以简单到一个单词、短语或表情符号。非常短的提示将在很大程度上依赖于 Midjourney 的默认样式。 完整 prompt:可以包括一个或多个图像链接、多个文本短语或单词,以及一个或多个后缀参数 Image Prompts: 可以将图像 URL 添加…...

uvm白皮书练习_ch2_ch223_加入objection机制
UVM中通过objection机制来控制验证平台的关闭。 在每个phase中,UVM会检查是否有objection被提起(raise_ objection),如果有,那么等待这个objection被撤销(drop_objection)后停止仿真;…...

利用C++开发一个迷你的英文单词录入和测试小程序-增强功能
小玩具基本完成之后,在日常工作中,记录一些单词,然后定时再复习下,还真的有那么一点点用(毕竟自己做的小玩具)。 在使用过程中,遇到不认识的单词,总去翻译软件翻译,然后…...

kibana启动报错
1.响应 超过时间30000ms (1) docker rm elasticsearch #从docker中删除es docker rm kibana #从docker中删除kibana (2)重新安装启动es加大最大运行内存 :1024M docker run --name elasticsearch -p 9200:9200 -p 9300:9300 \ -e "discovery.typesingle-node" \ -…...
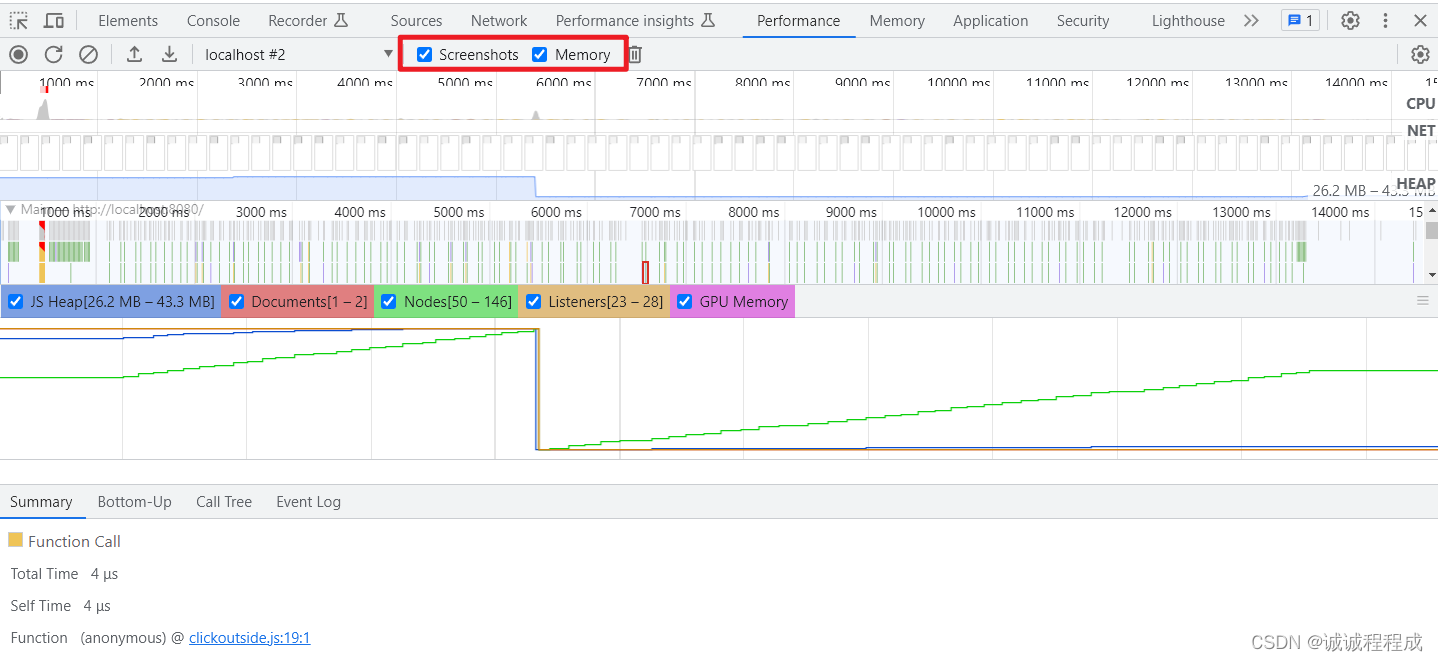
排查内存泄露
1 通过Performance确认是否存在内存泄露 一个存在内存泄露的 DEMO 代码: App.vue <template><div><button click"myFn" style"width: 200px; height: 200px;"></button><home v-if"ishow"></hom…...
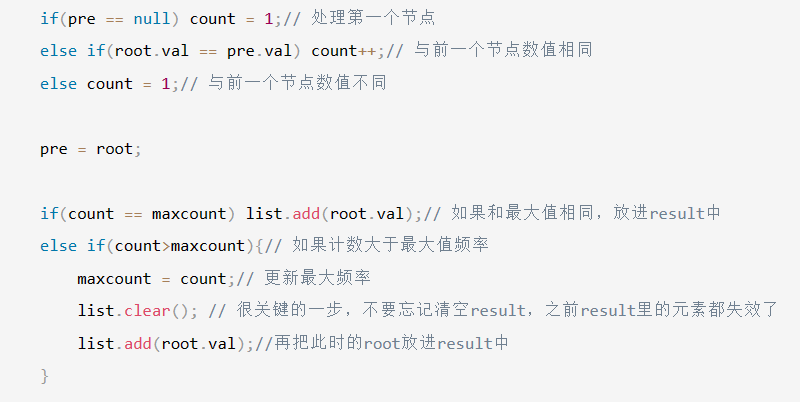
【LeetCode-简单题】501. 二叉搜索树中的众数
文章目录 题目方法一:暴力哈希方法二:利用二叉搜索树的特性(递归双指针) 题目 方法一:暴力哈希 这是针对于普通二叉树的解法 统计number出现次数 然后将次数最大的众数集 取出来 Map<Integer , Integer > map …...
MAC word 如何并列排列两张图片
系统:MAC os 参考博客 https://baijiahao.baidu.com/s?id1700824516945958911&wfrspider&forpc 步骤1 新建一个word文档和表格 修改表格属性 去掉自动重调尺寸以适应内容 插入图片 在表格的位置插入对应的图片如下 去除边框 最终结果如下...

PTA第三章作业题
文章目录 前言7-1 比较大小Ⅰ. 方法一 :直接判断法Ⅱ. 方法二:交换法 7-2 比较两个数的大小Ⅰ. 方法 :直接判断法 7-3 成绩等级Ⅰ. 方法 :直接判断法 7-4 打鱼晒网Ⅰ. 方法 :直接判断法 7-5 计算奖金Ⅰ. 方法 …...
vscode vue html 快捷键
css文件 选择多行 按下ctrl不放 按下鼠标滚轮不放(鼠标中键) 鼠标向下移动 同时修改多个相同的字符串 <style> .base-goods-item li {width: 304px;height: 404px;background-color: #eef9f4; } .base-goods-item li {display: block; } .base-…...

mysql锁相关的总结
1、参考文章 MySQL 主键索引在 RR 和 RC 隔离级别下的加锁情况总结_51CTO博客_mysql二级索引加锁 2、 show OPEN TABLES where In_use > 0; -- 类似rc的需求 show variables like innodb_locks_unsafe_for_binlog; SELECT * FROM INFORMATION_SCHEMA.INNODB_TRX; -- …...

计算机竞赛 深度学习乳腺癌分类
文章目录 1 前言2 前言3 数据集3.1 良性样本3.2 病变样本 4 开发环境5 代码实现5.1 实现流程5.2 部分代码实现5.2.1 导入库5.2.2 图像加载5.2.3 标记5.2.4 分组5.2.5 构建模型训练 6 分析指标6.1 精度,召回率和F1度量6.2 混淆矩阵 7 结果和结论8 最后 1 前言 &…...

docker-compose搭建的mysql,如何定时备份数据
一、前言 使用docker-compose搭建的mysql中自带了mysqldump,所以在服务器上如何使用容器中的mysqldump命令是实现备份的原理,下面是主要实现的命令 docker exec -it mysql mysqldump -u root -p$mysql_password $database_name > $backup_file二、备…...

webpack:关于处理html文件的插件html-webpack-plugin、add-asset-html-webpack-plugin
简介 add-asset-html-webpack-plugin 将 JavaScript或CSS文件添加到由html-webpack-plugin插件生成的HTML中去。 html-webpack-plugin 默认配置会在出口目录中(通过output.path选项配置)生成一个index.html文件; 生成的index.html文件将会…...

如何两个不同的脚本文件之间传递参数
两个不同的Shell脚本之间如何访问传递的参数取决于它们是如何调用的。如果一个Shell脚本1调用另一个Shell脚本2并且想要将参数传递给被调用的脚本2,可以使用以下方法: 方法1:通过位置参数传递参数 这是一种常见的方法,其中一个脚…...

一篇文章彻底搞懂熵、信息熵、KL散度、交叉熵、Softmax和交叉熵损失函数
文章目录 一、熵和信息熵1.1 概念1.2 信息熵公式 二、KL散度和交叉熵2.1 KL散度(相对熵)2.2 交叉熵 三、Softmax和交叉熵损失函数3.1 Softmax3.2 交叉熵损失函数 一、熵和信息熵 1.1 概念 1. 熵是一个物理学概念,它表示一个系统的不确定性程度,或者说是…...
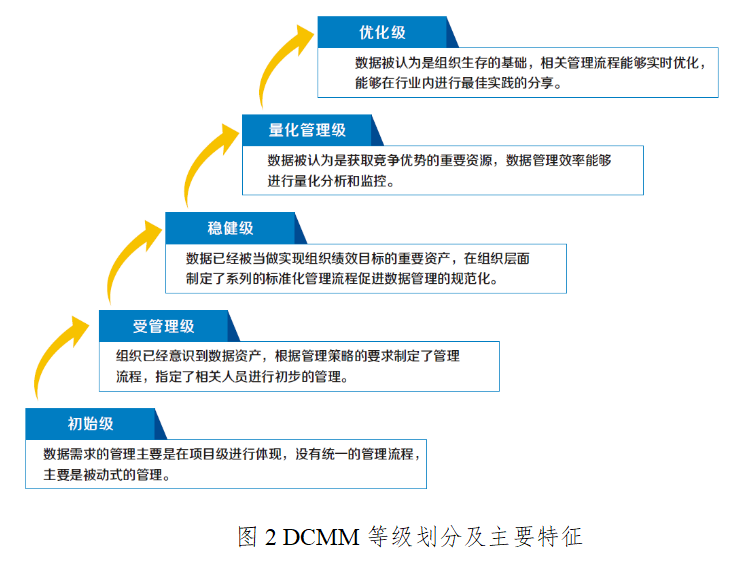
[架构之路-223]:数据管理能力成熟度评估模型DCMM简介
目录 一、背景 二、评估依据 三、评估内容 四、主要适用对象 五、能力等级 六、不同层次的文件: 一、背景 信息技术与经济社会的交汇融合引发了数据爆发式增长。数据蕴含着重要的价值,已成为国家基础性战略资源,正日益对全球生产、流通…...
)
十大排序算法的实现(C/C++)
以下是十大经典排序算法的简单 C 实现: 冒泡排序(Bubble Sort): 思想:重复地遍历要排序的列表,比较相邻的两个元素,如果它们的顺序错误就交换它们。时间复杂度:最坏情况和平均情况…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...
