(搞定)排序数据结构(1)插入排序 选择排序+冒泡排序
目录
本章内容如下
一:插入排序
1.1插入排序
1.2希尔排序
二:选择排序
2.1选择排序
三:交换排序
3.1冒泡排序
一:插入排序
1.1直接插入排序
说到排序,其实在我们生活中非常常见,比如当我们需要在网上买东西的时候, 我们可以按照价格排序,也可以按照销量进行排序,所以对于我们来说学习排序这个数据结构是非常重要的,在本文中,我会尽可能按照我的理解将目录中的排序给将清楚。
下面就是我在一个网购网站中进行截取的图片,我们可以看到排序无处不见。

现在让我们进入排序的讲解!!
首先我们讲解的是插入排序
首先我们来认识一下插入排序这个算法,插入排序顾名思义就是插入到前(n-1)个有序
数中,这就像我们生活中经常玩扑克牌的时候的思想,我们玩扑克牌的时候有一种摸牌
思路就是将第一张牌有序,然后让后面的牌进行插入使得我们的牌一直有序。
下面我通过一群数字来进行讲解
比如说我们的数组中的值为 9 4 7 2 5 3 1 6 8
这9个数字那么我们如何使得这个数组有序呢?
我们通过画图来进行讲解!!

很明显我们对于插入排序的思想
思路 :假设我们要插入第n个数,我们需要保证前n-1个数有序,然后再进行插入,没插入一个数我们就要将该数前面的数与要插入的数经行比较,如果大于这个要插入的数那我们就将他玩后面进行移动就可以了。
void InsertSort(int* a, int n)
{//使前n-1个数先有序,然后插入第n个数for (int i = 0; i < n-1; i++){int end = i;int tmp = a[end + 1];//一趟插入排序的思路while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp;}
}
现在让我们来算一下插入排序的时间复杂度,与空间复杂度吧。
时间复杂度最好:O(N), 最坏:O(n^2)
首先我们不难发现它的空间复杂度为O(1)
最坏时间复杂度:O(n^2),当一个数组为逆序的时候,就是插入排序的最坏的
情况,在这种情况下我们一共有N个数字,插入一个数我们就需要将前面的
数字全部像后面进行移动一次,然后在插入所以总共来说就是N*N.
最好的情况是什么呢,最好的情况当然是当数组顺序有序的时候,每一个数
只要插入就行了,而不需要移动元素,插入的时间复杂度为O(1),所以总共
的时间复杂度为O(1*N)=O(N).
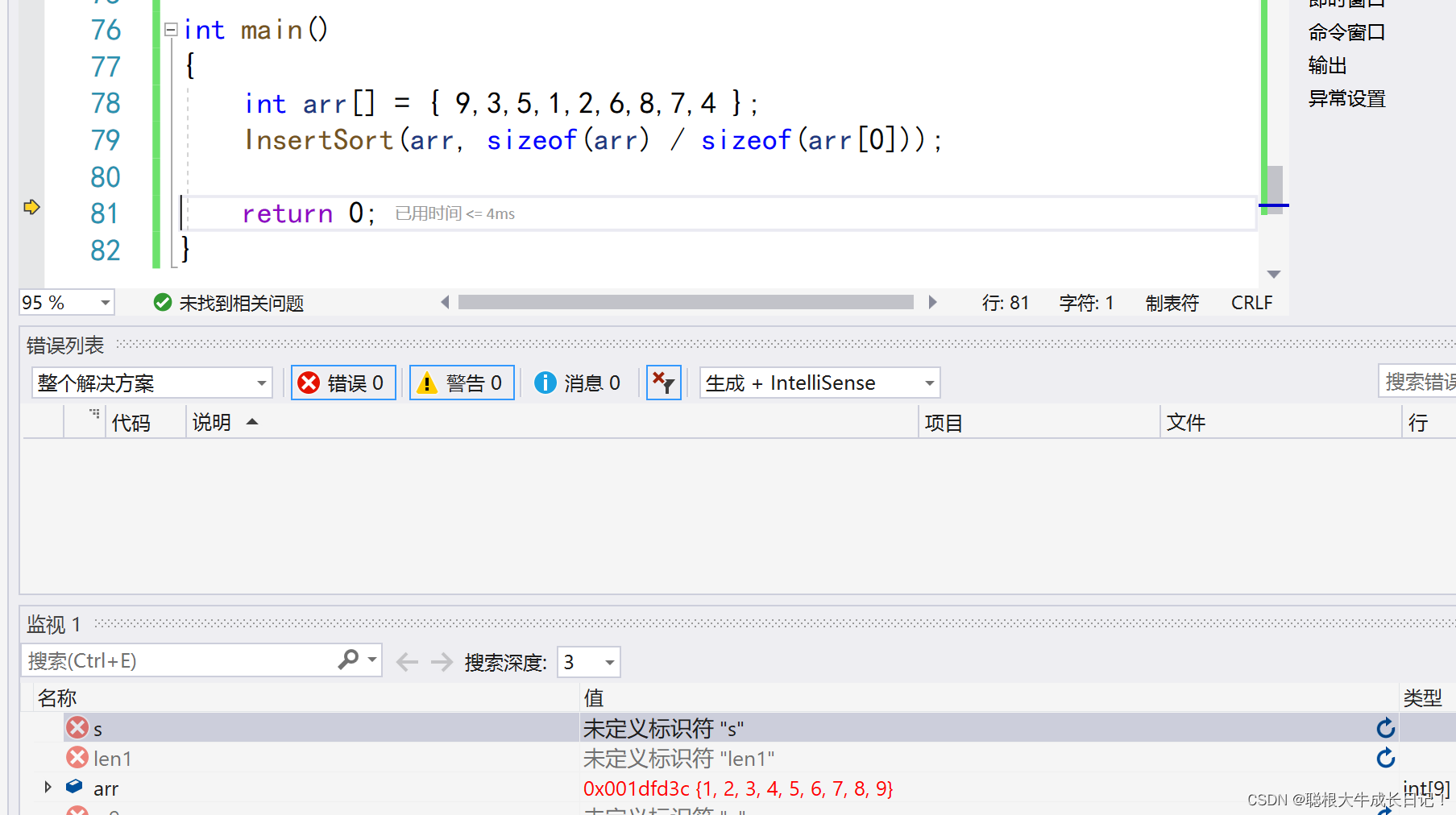
1.2希尔排序
其实希尔排序的本质也是插入排序,希尔排序只是在插入排序上进行的一个优化的
排序我们在上面的插入排序中不难发现,当数组有序的时候,我们的插入排序的
时间复杂度是非常好的为O(N),而我们的希尔大佬就是看到了这个特点,
所以就在插入排序中进行了优化,才有了我们著名的一个排序算法叫做希尔排序。
希尔排序的思想是什么呢?
其实希尔排序的思想其实也非常简单 先预排序,在直接插入排序。
1:先对数组进行多组预排序,使得数组中的一些子数组接近有序。
2:在对数组进行插入排序。
我们用图来讲解一组预排序
我们不难看出在进行一组预排序完成后我们的数组相对于原来的数组就接近有序了,
且gap越小的时候我们的数组越接近有序,当gap==1的时候我们的,我们的预排序
就是直接插入排序。
代码如下:
//版本一
void ShellSort(int* a, int n)
{int k = 0;int gap = n;while(gap!=1){gap /= 2;//最后一次gap一定等于1//多组预排序,也就是我们图中红黑绿三组进行预排序for (int j = 0; j < gap; j++){//一组预排序操作for (int i = 0; i < n - gap; i += gap){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}}}``````c
```版本二:有点像优化的版本
void ShellSort(int* a, int n)
{int k = 0;int gap = n;while(gap!=1){gap=gap/3 +1;//最后一次gap一定等于1 //间距为gap的值从前往后直接进行交换for (int i = 0; i < n - gap; i ++){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}}

希尔排序的时间复杂度是多少呢?
其实书上也没有给出明确的证明,有很多种不同的看法,但是差不多是O(N^1.3),这个我也不会证明,需要涉及到高阶的数学。
大家如果有兴趣的话可以去证明一下。
到这里我们的插入排序就讲解完毕了,希尔排序需要大家自行的去画图,多思考。
--------
二:选择排序
其实我们的选择排序有两种,一种是直接选择排序,也是我们讲解的排序,还有一种就是堆排序,而堆排序我们之前已经讲解过了,如果你还没看的话建议先直接去补一下。
堆排序链接:https://blog.csdn.net/2201_75964502/article/details/133017420?spm=1001.2014.3001.5501
在这里我们主要讲解选择排序的优化版本,就是我们遍历一边数组,选出两个值,
一个最大值我们往后面插入,还有一个最小值玩前面插入。
直到我们将数组排序好就可以了。
思想:遍历一遍选最大值与最小值,然后排序就行了。
图:这里只写了1个步骤
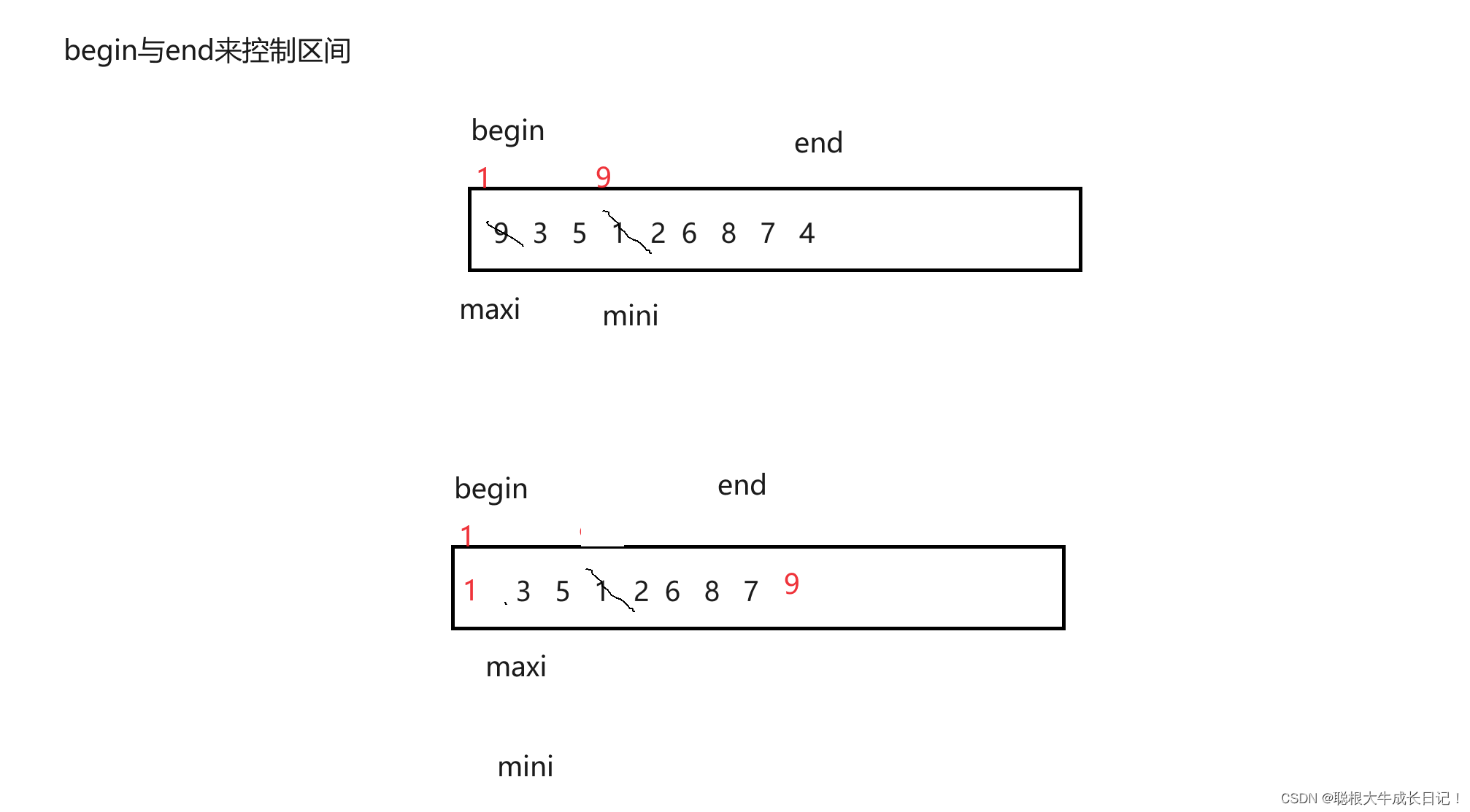
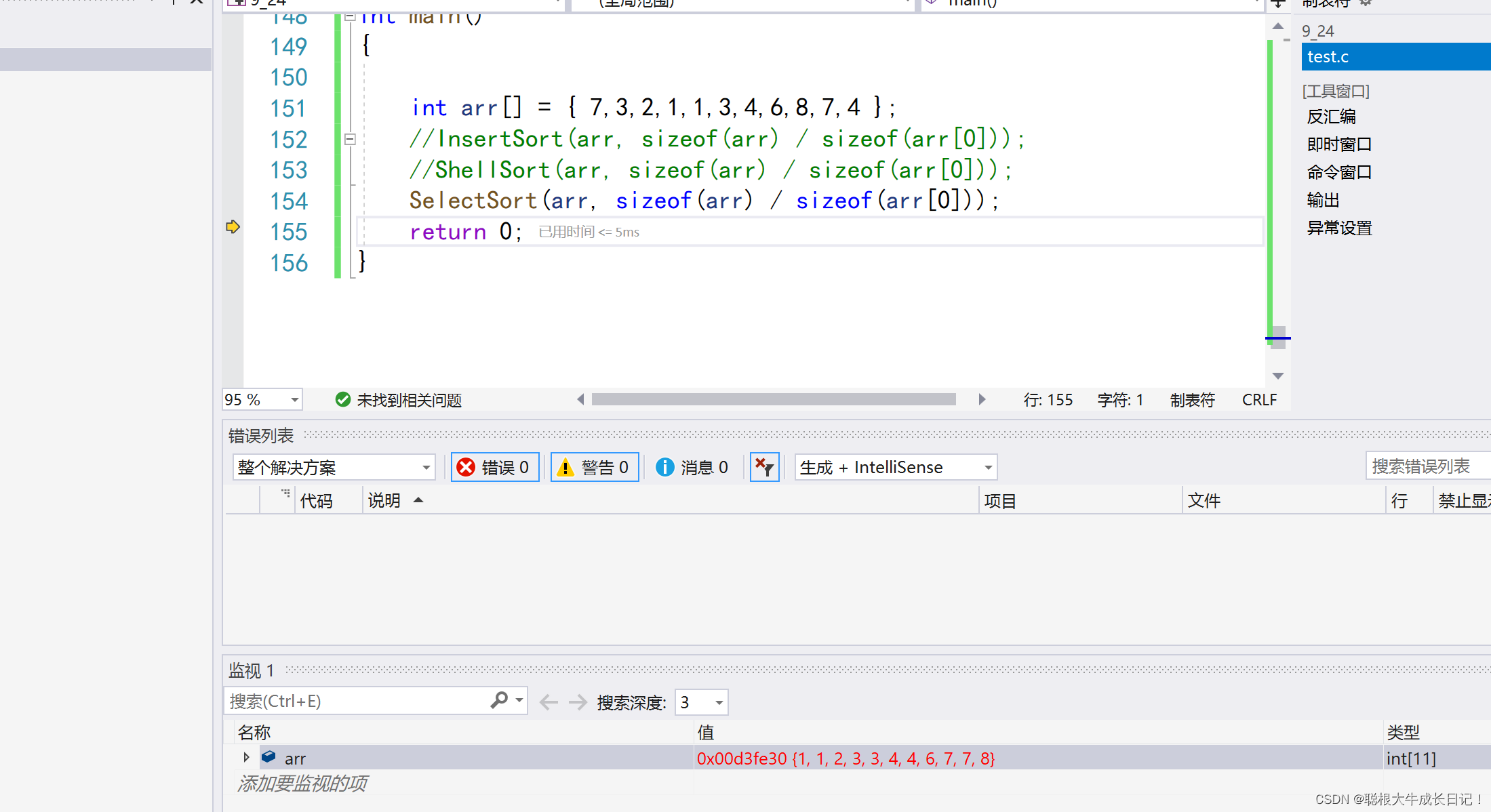
代码如下:
void SelectSort(int* a, int n)
{int begin = 0;int end = n-1;while (begin < end){int maxi = begin;int mini = begin;for(int i =begin;i<=end;i++){//选最小的下标if (a[mini] > a[i]){mini = i;}//选最大的下标if (a[maxi] < a[i]){maxi = i;}}Swap(&a[begin], &a[mini]);//防止最大值就在begin处if (begin == maxi){maxi = mini;}Swap(&a[maxi], &a[end]);begin++;end--;}
}
选择排序的时间复杂度:O(^2)
因为它的时间复杂度算法是一个等差数列:(n)+(n-2)_......+2+0
每次都需要遍历数组选两个值,固定的
所以选择排序是很稳定的。
-------
三:交换排序
其实我们的交换排序也有两种,一种是快速排序,另外一种就是我们本章所讲解的
冒泡排序,而我们的快速排序由于有几种方法,且有点难,所以我会独自整理成一篇
文章来进行讲解我们的快速排序。
其实冒泡排序可能是我们见过最多的一种排序,它的思想并不难理解
冒泡排序的思想是什么呢?
思想:
遍历一遍数组,两两相邻的元素进行比较,将数组中最大元素的值给冒到最
后去,一直遍历,直到数组变成有序的数组
代码如下:
void BubbleSort(int* a, int n)
{int i = 0;//一共冒泡几趟for (int i = 0; i < n-1; i++){int exchange = 1;//一趟内部for (int j = 0; j < n-i-1; j++){if (a[j] > a[j + 1]){exchange = 0;Swap(&a[j], &a[j + 1]);}}if (exchange == 1){//说明原数组有序,就不需要进行排序了break;}}}
冒泡排序的时间复杂度:O(N^2)
它非常稳定。,因为时间复杂度是固定的
感谢大家的观看,如果你觉得对你有帮助的话,可以给博主一个赞哦!!
相关文章:

(搞定)排序数据结构(1)插入排序 选择排序+冒泡排序
目录 本章内容如下 一:插入排序 1.1插入排序 1.2希尔排序 二:选择排序 2.1选择排序 三:交换排序 3.1冒泡排序 一:插入排序 1.1直接插入排序 说到排序,其实在我们生活中非常常见&…...

C++ 类访问修饰符 public、private、protected
数据封装是面向对象编程的一个重要特点,它防止函数直接访问类类型的内部成员。类成员的访问限制是通过在类主体内部对各个区域标记 public、private、protected 来指定的。关键字 public、private、protected 称为访问修饰符。 一个类可以有多个 public、protected…...
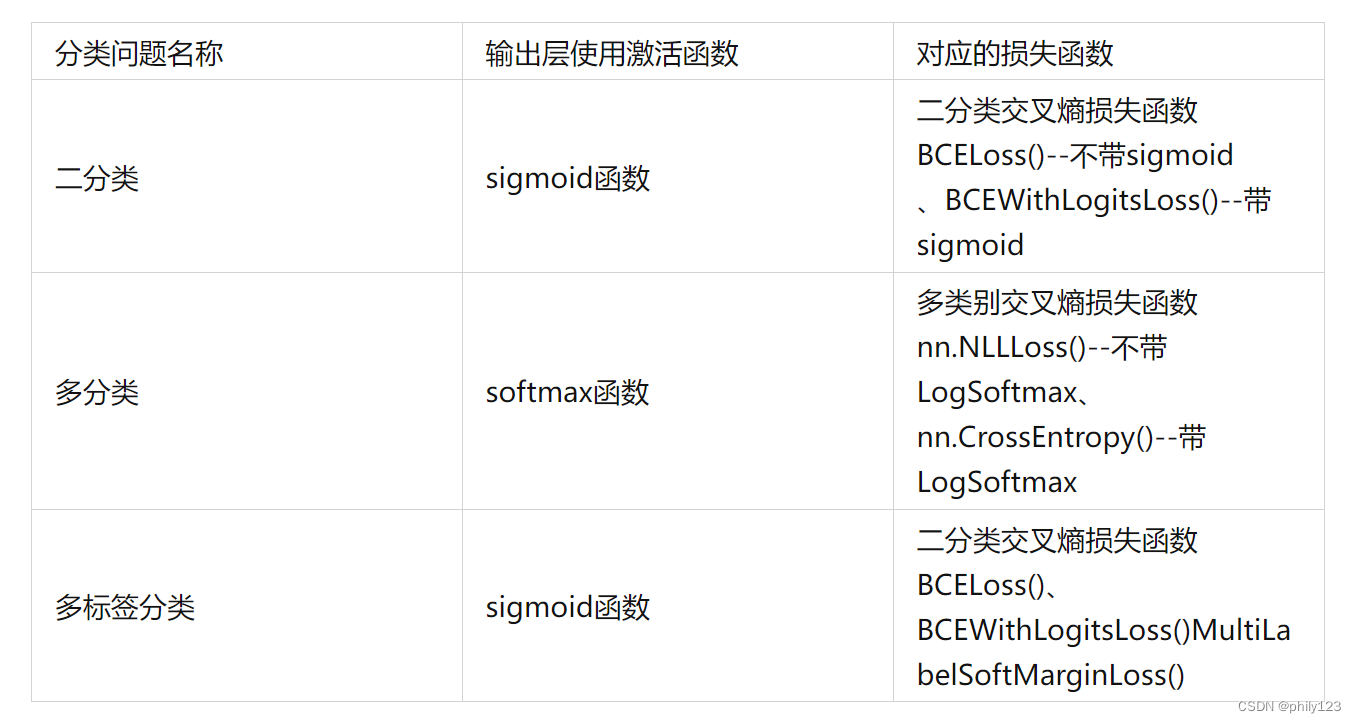
pytorch学习笔记——BCE与CE
BCELoss的话只需要网络输出一个通道,CE Loss(Cross Entropy Loss)需要输出n_class个通道。 对于二分类任务可以使用CE Loss输出两个通道,也可以使用BCE Loss输出一个通道。 https://www.jianshu.com/p/5b01705368bb https://zhuanlan.zhihu.com/p/372628…...
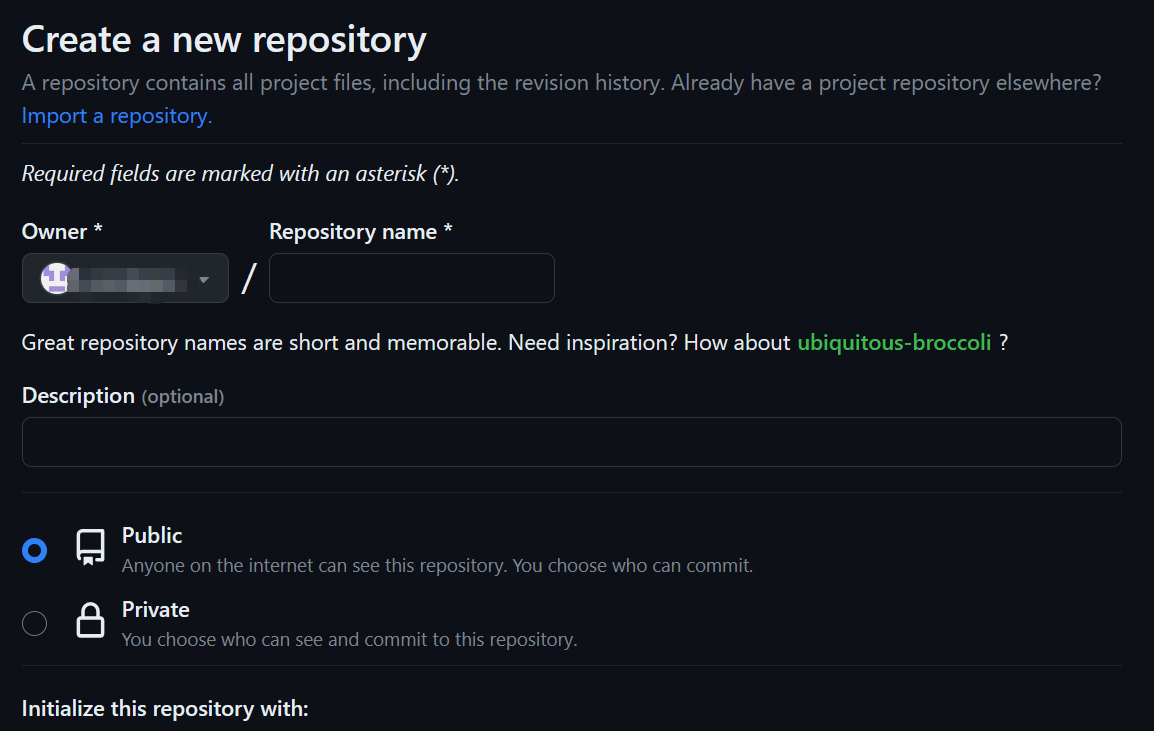
win使用git(保姆级教程)
序言 上学期间用的git并不多,但是从研三实习以及后面工作来看,git是一项必备技能,所以在此来学习一下。 下载git安装包 打开网站,根据需求来下载;一般按照如下方式进行下载: 然后安装的时候记得按下图勾…...
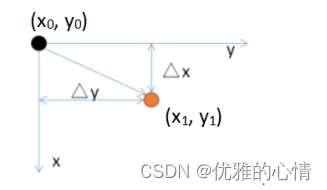
Python图像处理-----几何变换
文章目录 一、图像几何变换理论二、图像平移2.1 使用数学公式的实现方式为:2.2 使用矩阵实现的方式为2.3 使用opencv三、图像缩放3.1 用数学式子表示为公式(a为缩放系数):3.2 用矩阵表示如公式所示:一、图像几何变换理论 图像几何变换不改变图像的像素值,在图像平面上进行像…...

如何正确选择研究方向?如何实现论文创新?
学术评价是遵循“质量第一”原则的,所以对于研究生来说,从一开始就要把路子走正,自觉树立精品意识,把精力高度集中到提高学位论文的质量上来。这里,根据本人多年来指导博士和硕士研究生的体会,就人文社科研究生学位论文的选题与创新略述管见。 学位论文选题的两个层面 …...
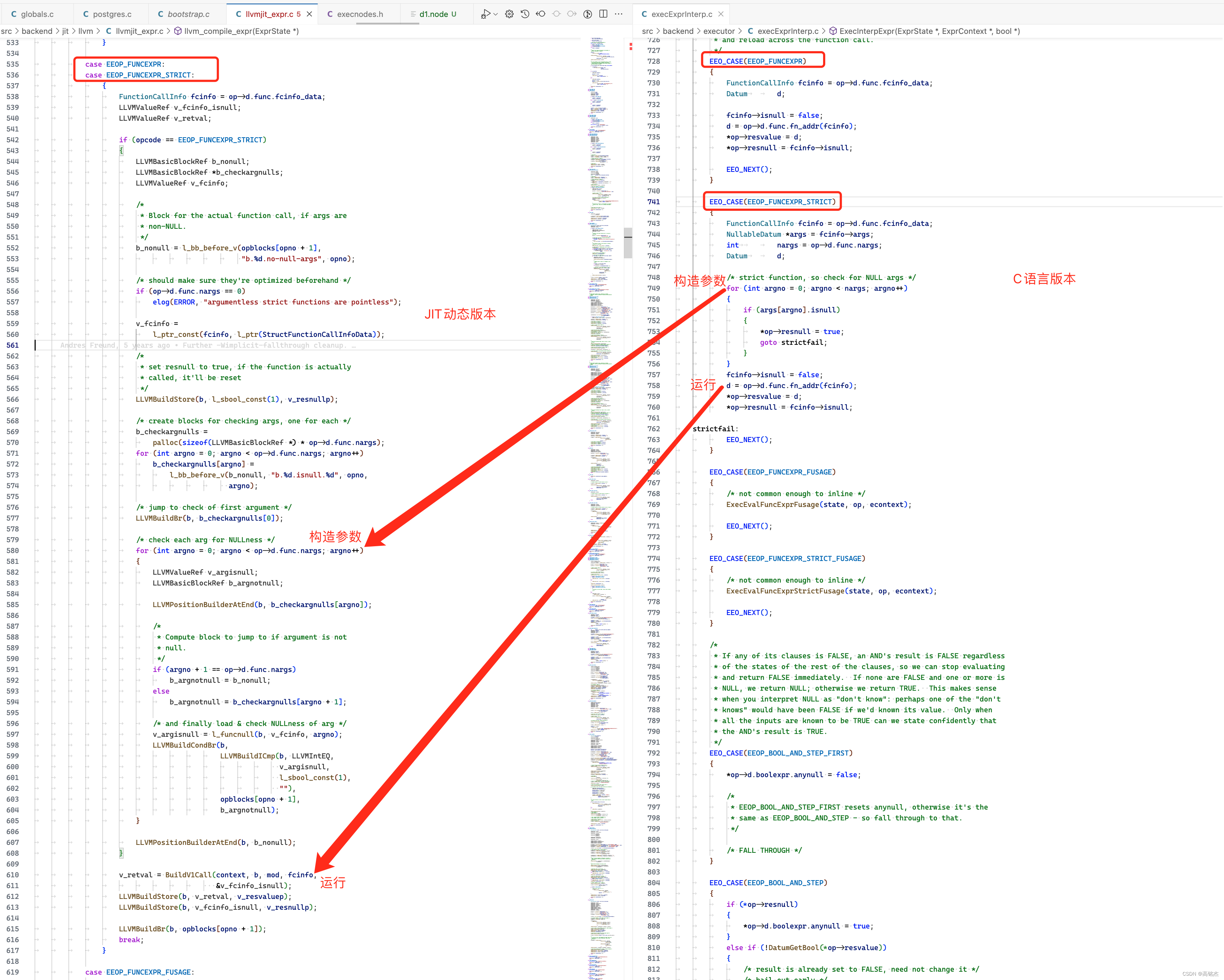
Postgresql源码(113)表达式JIT计算简单分析
相关 《Postgresql源码(85)查询执行——表达式解析器分析(select 11如何执行)》 《Postgresql源码(113)表达式JIT计算简单分析》 1 普通表达式计算 普通表达式计算发生在优化器preprocess_expression中&am…...

CMU15-213 课程笔记 04-Floating Point
文章目录 浮点数如何用二进制表示IEEE 浮点数标准IEEE 浮点数实现IEEE 浮点数在内存里 E exp - bias 计算指数M 1.xxx 尾数计算举例:对一个浮点数进行转换一些关于浮点数的计算等等 浮点数如何用二进制表示 计算机内部的浮点数不是这样存在内存里的(至…...
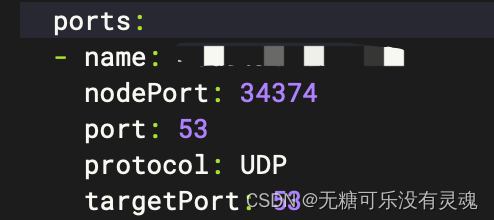
DockerKubernetes ❀ Service下Port端口区分
文章目录 概述案例 概述 在Kubernetes中,Service(svc)是一种抽象机制,用于将一组 Pod 暴露给其他应用程序或服务。Service 可以有三种类型的端口: nodePort:这是 Service 在节点上公开的端口。可以使用此…...

【C++】笔试训练(一)
目录 一、选择题二、编程1、组队竞赛2、删除公共字符 一、选择题 1、以下for循环的执行次数是() for (int x 0, y 0; (y 123) && (x < 4); x);A 是无限循环 B 循环次数不定 C 4次 D 3次 答案:C 2、以下程序的运行结果是&…...
)
数据结构与算法之集合: Leetcode 349. 两个数组的交集 (Typescript版)
两个数组的交集 https://leetcode.cn/problems/intersection-of-two-arrays/description/ 描述 给定两个数组 nums1 和 nums2 ,返回 它们的交集 。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序 。 示例 1 输入:nums1 [1,2,…...
Unity 内存性能分析器 (Memory Profiler)
一、 安装 安装有两种方式一: add package : com.unity.memoryprofiler方式二: From Packages : Unity Registry 搜索 Memory Profiler 二、 使用 打开:Windows - > Analysis - > Memory Profiler 打开MemoryProfiler界面࿰…...

前端携带Bearer Token
前端携带Bearer Token 在前端使用 axios 发送请求时,可以通过设置请求头来携带 Bearer Token。Bearer Token 是一种常用的身份验证方式,它通常用于 OAuth2 授权流程中。 要在 axios 中携带 Bearer Token,可以通过设置 Authorization 请求头…...

leetcode 周赛 364
参考视频: 单调栈【力扣周赛 364】 文章目录 8048. 最大二进制奇数100049. 美丽塔 I100048. 美丽塔 II100047. 统计树中的合法路径数目 8048. 最大二进制奇数 题目链接 给你一个 二进制 字符串 s ,其中至少包含一个 1 。 你必须按某种方式 重新排列 字…...
开机自启动Linux and windows
1、背景 服务器由于更新等原因重启,部署到该服务上的响应的应用需要自启动 2、Linux 2.1 方式一 编写启动应用的sh脚本授权该脚本权限 chmod 777 xxx.sh 修改rc.loacl 位置:/etc/rc.local 脚本:sh /home/xxxx.sh & 授权rc.local …...

科技云报道:大模型的阴面:无法忽视的安全隐忧
科技云报道原创。 在AI大模型的身上,竟也出现了“to be or not to be”问题。 争议是伴随着大模型的能力惊艳四座而来的,争议的核心问题在于安全。安全有两个方面,一个是大模型带来的对人类伦理的思考,一个是大模型本身带来的隐…...

2023年前端流行什么技术和框架了?
Web前端三大主流框架有React、Vue.js和Angular,由于接触过Vue.js,接下来主讲最新的Vue3.0! Vue3.0作为最新版本的Vue.js框架,拥有更强大的性能和更丰富的功能,为低代码开发平台注入了全新的活力。而JNPF快速开发平台作…...

Nginx 背锅解析漏洞
Nginx 背锅解析漏洞 文章目录 Nginx 背锅解析漏洞1 在线漏洞解读:2 环境搭建3 影响版本:4 漏洞复现4.1 访问页面4.2 上传文件 4.3 上传失败4.4 使用bp进行分析包4.5 对返回图片位置进行访问4.6 执行php代码技巧-图片后缀加./php4.7 分析原因 --》cgi.fix_pathinfo--…...

AI与传统数据库 - ChatGPT风过之后 | 从Duet AI说开来
作者:Ni Demai,是NineData数据库产品专家,曾任阿里云数据库国际产品总负责人,华为高斯 GaussDB 创始团队核心架构师,IBM Db2 资深研发工程师。 Demai 专注 Cloud-Native database 架构设计,分析型 MPP&…...

L1-032 Left-pad C++解法
一、题目再现 根据新浪微博上的消息,有一位开发者不满NPM(Node Package Manager)的做法,收回了自己的开源代码,其中包括一个叫left-pad的模块,就是这个模块把javascript里面的React/Babel干瘫痪了。这是个…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...
