【算法思想】贪心
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。
- 推荐:kuan 的首页,持续学习,不断总结,共同进步,活到老学到老
- 导航
- 檀越剑指大厂系列:全面总结 java 核心技术点,如集合,jvm,并发编程 redis,kafka,Spring,微服务,Netty 等
- 常用开发工具系列:罗列常用的开发工具,如 IDEA,Mac,Alfred,electerm,Git,typora,apifox 等
- 数据库系列:详细总结了常用数据库 mysql 技术点,以及工作中遇到的 mysql 问题等
- 懒人运维系列:总结好用的命令,解放双手不香吗?能用一个命令完成绝不用两个操作
- 数据结构与算法系列:总结数据结构和算法,不同类型针对性训练,提升编程思维,剑指大厂
非常期待和您一起在这个小小的网络世界里共同探索、学习和成长。💝💝💝 ✨✨ 欢迎订阅本专栏 ✨✨
博客目录
- 一.介绍
- 1.什么是贪心算法?
- 2.步骤
- 3.应用
- 2.贪心模版
- 二.贪心的例子
- 1.Dijkstra
- 2.Prim
- 3.Kruskal
- 4.其它贪心的例子
- 5.常见问题及解答
一.介绍
1.什么是贪心算法?
贪心算法(Greedy Algorithm)是一种常见的问题求解策略,通常用于优化问题。贪心算法的核心思想是在每一步都做出当前看起来最优的选择,而不考虑全局最优解。贪心算法通常适用于那些具有贪心选择性质的问题,即局部最优解也是全局最优解的一部分。
称之为贪心算法或贪婪算法,核心思想是
- 将寻找最优解的问题分为若干个步骤
- 每一步骤都采用贪心原则,选取当前最优解
- 因为没有考虑所有可能,局部最优的堆叠不一定让最终解最优
2.步骤
贪心算法是一种在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择,从而希望导致结果是最好或最优的算法。这种算法通常用于求解优化问题,如最小生成树、背包问题等。
以下是贪心算法的一般特点和步骤:
-
选择策略:从问题的所有可行选择中,选择当前看起来最优的一个。这个选择通常基于一定的规则或者评估函数。
-
可行性检验:检查所做的选择是否合法,即是否满足问题的约束条件。
-
局部最优性:贪心算法只关注当前步骤的最优解,而不考虑整体问题的最优解。这是贪心算法与动态规划等其他算法的主要不同之处。
-
迭代:重复执行步骤 1 和步骤 2,直到达到问题的结束条件或者找到一个近似的解。
3.应用
贪心算法的应用范围广泛,可以用于解决许多优化问题,如:
最小生成树问题:如 Kruskal 算法和 Prim 算法用于构建最小生成树。最短路径问题:如 Dijkstra 算法和 Bellman-Ford 算法用于寻找最短路径。调度问题:如任务调度、会议安排等。背包问题:给定一组物品和一个背包,每个物品有一定的重量和价值,要求在不超过背包容量的情况下,尽可能多地装入物品。活动选择问题:在一个活动集合中,每次只能参加一个活动,问如何安排时间以最大化所有活动的收益。编辑距离问题:给定两个字符串,求它们之间的最小编辑距离(即将一个字符串转换为另一个字符串所需的最少操作次数)。网络流问题:给定一张有向图和一些起点和终点,求最大流量。找零问题:给定一定数量的硬币和需要找零的金额,求使用最少的硬币数。
贪心算法的优点在于它们通常比其他复杂算法更快,因为它们不需要考虑所有可能的解决方案。然而,贪心算法的局限性在于它们不能保证一定找到全局最优解,因此在某些情况下可能会得到次优解或者不可行解。因此,在使用贪心算法时,需要仔细分析问题的特性,以确定它是否适合使用贪心策略。有时候,贪心算法可以与其他算法结合使用,以获得更好的结果。
2.贪心模版
下面是一个使用 Java 编写的通用贪心算法模板,你可以根据具体问题进行适当的修改和扩展:
import java.util.Arrays;public class GreedyAlgorithm {public static void main(String[] args) {// 在这里输入问题的输入数据// 例如,如果是一个数组或者列表,可以这样初始化:int[] inputArray = {5, 2, 1, 9, 3};// 调用贪心算法函数int result = greedyAlgorithm(inputArray);// 输出结果System.out.println("最终结果: " + result);}public static int greedyAlgorithm(int[] input) {// 在这里实现贪心算法的逻辑// 请根据问题的具体要求编写贪心策略// 以下是一个简单的示例:找到数组中的最小元素int minElement = input[0];for (int i = 1; i < input.length; i++) {if (input[i] < minElement) {minElement = input[i];}}return minElement;}
}
这个模板中,你可以将问题特定的输入数据放在main函数中,然后调用greedyAlgorithm函数来执行贪心算法。在greedyAlgorithm函数中,你需要根据问题的特性编写相应的贪心策略。
请注意,这只是一个基本的模板,实际上,贪心算法的实现会根据具体问题的不同而有所不同。你需要根据问题的需求来设计合适的贪心策略,并根据具体情况修改模板。
二.贪心的例子
1.Dijkstra
// ...
while (!list.isEmpty()) {// 选取当前【距离最小】的顶点Vertex curr = chooseMinDistVertex(list);// 更新当前顶点邻居距离updateNeighboursDist(curr);// 移除当前顶点list.remove(curr);// 标记当前顶点已经处理过curr.visited = true;
}
- 没找到最短路径的例子:负边存在时,可能得不到正确解
- 问题出在贪心的原则会认为本次已经找到了该顶点的最短路径,下次不会再处理它(curr.visited = true)
- 与之对比,Bellman-Ford 并没有考虑局部距离最小的顶点,而是每次都处理所有边,所以不会出错,当然效率不如 Dijkstra
2.Prim
// ...
while (!list.isEmpty()) {// 选取当前【距离最小】的顶点Vertex curr = chooseMinDistVertex(list);// 更新当前顶点邻居距离updateNeighboursDist(curr);// 移除当前顶点list.remove(curr);// 标记当前顶点已经处理过curr.visited = true;
}
3.Kruskal
// ...
while (list.size() < size - 1) {// 选取当前【距离最短】的边Edge poll = queue.poll();// 判断两个集合是否相交int i = set.find(poll.start);int j = set.find(poll.end);if (i != j) { // 未相交list.add(poll);set.union(i, j); // 相交}
}
4.其它贪心的例子
-
选择排序、堆排序
-
拓扑排序
-
并查集合中的 union by size 和 union by height
-
哈夫曼编码
-
钱币找零,英文搜索关键字
- change-making problem
- find Minimum number of Coins
-
任务编排
-
求复杂问题的近似解
5.常见问题及解答
- 贪心算法一定会找到最优解吗?
答:不一定。贪心算法只保证在每一步选择中都是最优的,但并不能保证整个问题的最优解。例如,背包问题中的贪心算法可能会导致最后一个物品没有被装入背包。 - 如何判断一个问题是否适合用贪心算法解决?
答:一个问题如果可以用递归的方式分解成若干个子问题,且每个子问题都有明确的最优解(即局部最优),那么这个问题就可以用贪心算法解决。 - 贪心算法的时间复杂度是多少?
答:贪心算法的时间复杂度取决于问题的规模和具体实现。一般来说,对于规模较小的问题,贪心算法的时间复杂度可以达到 O(nlogn)或 O(n^2);对于规模较大的问题,可能需要 O(n^3)或更高。
觉得有用的话点个赞
👍🏻呗。
❤️❤️❤️本人水平有限,如有纰漏,欢迎各位大佬评论批评指正!😄😄😄💘💘💘如果觉得这篇文对你有帮助的话,也请给个点赞、收藏下吧,非常感谢!👍 👍 👍
🔥🔥🔥Stay Hungry Stay Foolish 道阻且长,行则将至,让我们一起加油吧!🌙🌙🌙
相关文章:

【算法思想】贪心
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kuan 的首页,持续学…...

freeswitch-01
文章目录 1. 电话实现技术2. 模拟信号与数字信号2.1 模拟信号2.2 数字信号 3. PCM4. 局间中继与电路复用技术5. 信令5.1 定义5.2 分类5.2.1 功能分类5.2.2 工作区域分类5.2.3 信道分类 5.3 用户线信令5.4 局间信令5.5 七号信令5.6 H.323与SIP信令 6. 媒体6.1 定义 7. 电路交换与…...
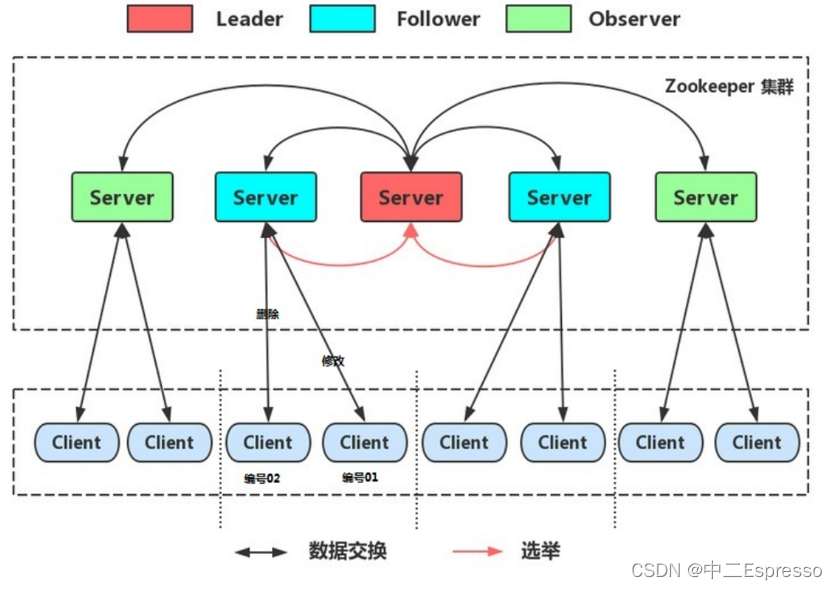
Zookeeper-集群介绍与核心理论
Zookeeper集群 4.Zookeeper集群4.1) 介绍4.2) 核心理论 4.Zookeeper集群 4.1) 介绍 Leader选举: Serverid:服务器ID。比如有三台服务器,编号分别是1,2,3。编号越大在选择算法中的权重越大。Zxid:数据ID。服务器中存放的最大数据…...

动态分配的内存位置在哪里?
在C++中,动态分配的内存位于称为堆(Heap)的内存区域。以下是一些关于堆和其他相关内存区域的基本信息: 堆(Heap): 这是一个用于动态内存分配的内存区域。使用new(C++)或malloc(C)等函数从堆中分配内存,并使用delete(C++)或free(C)释放这些内存。堆的大小通常受…...

Vue3中的Ref与Reactive:深入理解响应式编程
前言 Vue 3是一个功能强大的前端框架,它引入了一些令人兴奋的新特性,其中最引人注目的是ref和reactive。这两个API是Vue 3中响应式编程的核心,本文将深入探讨它们的用法和差异。 什么是响应式编程? 在Vue中,响应式编…...
Windows10/11显示文件扩展名 修改文件后缀名教程
前言 写这篇文章的原因是由于我分享的教程中的文件、安装包基本都是存在阿里云盘的,下载后需要改后缀名才能使用。 但是好多同学不会改。。 Windows 10 随便打开一个文件夹,在上方工具栏点击 “查看”点击 “查看” 后下方会显示更详细的工具栏然后点…...

【C++】手撕string(string的模拟实现)
手撕string目录: 一、 Member functions 1.1 constructor 1.2 Copy constructor(代码重构:传统写法和现代写法) 1.3 operator(代码重构:现代写法超级牛逼) 1.4 destructor 二、Other mem…...

用python3编译cv_bridge
文章目录 概要依赖工作空间编译可能遇到的问题error: option --install-layout not recognized概要 当我在编写一个使用传感器图像传输和OpenCV4的ROS包时,从构建到编译代码的一切都很顺利。当我开始运行节点本身时,问题出现了,它给出了以下错误: Assertion failed (tlsSl…...

招商信诺人寿基于 Apache Doris 统一 OLAP 技术栈实践
本文导读: 当前,大数据、人工智能、云计算等技术应用正在推动保险科技发展,加速保险行业数字化进程。在这一背景下,招商信诺不断探索如何将多元数据融合扩充,以赋能代理人掌握更加详实的用户线索,并将智能…...

我的python安装在哪儿了?python安装路径怎么查?
对于 Python 开发者来说,Windows 系统中的 Python 安装路径是非常重要的。在本文中,我们将从多个方面探究如何查看 Python 安装路径,并提供代码示例。 一、使用文件浏览器查看 Python 安装路径 在 Windows 系统中,我们可以使用文…...

视频汇聚/安防监控平台EasyCVR指定到新的硬盘进行存储录像,如何自动挂载该磁盘?
TSINGSEE青犀视频监控汇聚平台EasyCVR可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有国标GB28181、RTSP/Onvif、RTMP等,以及支持厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等。平台既具备传统安防视频监控的能力&…...

读博时的建议或心得
https://www.zhihu.com/question/32210068/answer/264273093 读论文:一开始读论文,一定要读顶会顶刊的,以后也一直要这样。如此,一方面保持了研究的水准,时刻提醒自己:我就是混这个层次的。另一方面&#…...

3分钟,免费制作一个炫酷实用的数据可视化大屏!
在当前大数据时代背景下,数据已成为在工业革命中如同煤炭、石油一般宝贵的资源。但是由于数据越来越庞大、越来越复杂,导致数据的可读性也越来越低。因此,对数据可视化的需求也越来越高,需要解决的问题也越来越复杂,而…...

自费访学|金融公司高管赴世界名校伯克利交流
R经理决定抽出一年时间,自费赴美国访学,向国外导师请教,探讨了解不同社会环境下,各种经济及社会现象的产生和发展,在思维碰撞中提升自身的国际视野。最终我们为其联系到世界名校-加州大学伯克利分校,导师为…...

Databend 开源周报第112期
Databend 是一款现代云数仓。专为弹性和高效设计,为您的大规模分析需求保驾护航。自由且开源。即刻体验云服务:https://app.databend.cn 。 Whats On In Databend 探索 Databend 本周新进展,遇到更贴近你心意的 Databend 。 理解用户自定义…...

如何学习maya mel语言的经验分享
一、前言 总结一下这十几年来学习和使用mel语言的一些经验,供初学朋参考,哈哈。 这里不说深奥理论,只是朴实经历陈述。 其实,早在2003年,最初接触maya时,就已经涉及到mel的学习,当时在大学里接…...

睿趣科技:新手抖音开店卖什么产品好
抖音已经成为了一款年轻人热爱的社交媒体应用,同时也成为了一种全新的电商平台。对于新手来说,抖音开店卖什么产品是一个备受关注的问题。在这篇文章中,我们将探讨一些适合新手的产品选择,帮助他们在抖音上开店获得成功。 流行时尚…...

【新版】系统架构设计师 - 案例分析 - 架构设计<Web架构>
个人总结,仅供参考,欢迎加好友一起讨论 文章目录 架构 - 案例分析 - 架构设计<Web架构>Web架构知识点单台机器 到 数据库与Web服务器分离应用服务器集群负载均衡负载均衡技术静态与动态算法Session共享机制有状态与无状态 持久化技…...
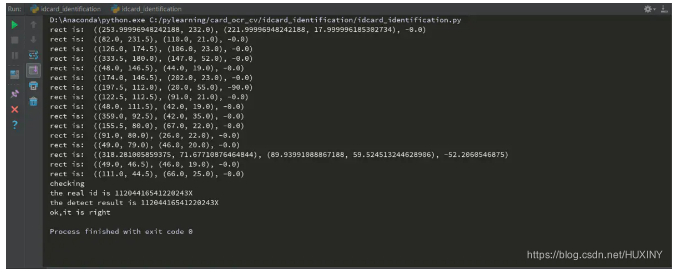
竞赛选题 基于视觉的身份证识别系统
0 前言 🔥 优质竞赛项目系列,今天要分享的是 基于机器视觉的身份证识别系统 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐! 🧿 更多资料, 项目分享: https://gitee.com/dancheng-sen…...

git详细教程
git详细教程 区域划分单分支操作git log语法常用的参数及其详解git log 结果 git refloggit diff常用的参数及其详解 git reset常用的参数及其详解 git checkoutgit rm常用的参数及其详解 git remote常用的参数及其详解 多分支切换代码融合git switch常用的参数及其详解 git br…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
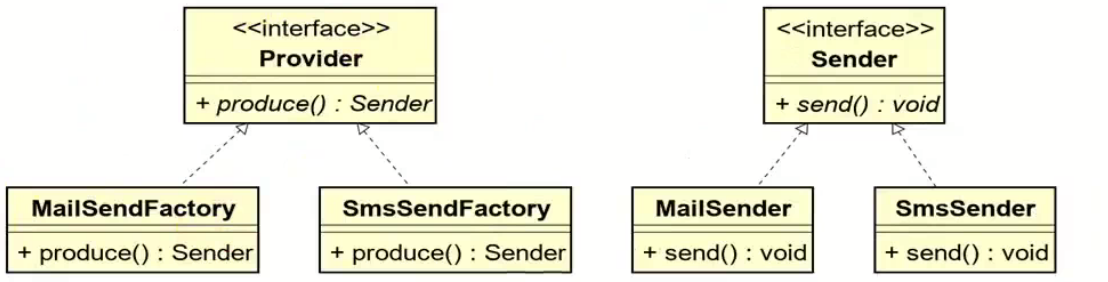
工厂方法模式和抽象工厂方法模式的battle
1.案例直接上手 在这个案例里面,我们会实现这个普通的工厂方法,并且对比这个普通工厂方法和我们直接创建对象的差别在哪里,为什么需要一个工厂: 下面的这个是我们的这个案例里面涉及到的接口和对应的实现类: 两个发…...
运行vue项目报错 errors and 0 warnings potentially fixable with the `--fix` option.
报错 找到package.json文件 找到这个修改成 "lint": "eslint --fix --ext .js,.vue src" 为elsint有配置结尾换行符,最后运行:npm run lint --fix...

21-Oracle 23 ai-Automatic SQL Plan Management(SPM)
小伙伴们,有没有迁移数据库完毕后或是突然某一天在同一个实例上同样的SQL, 性能不一样了、业务反馈卡顿、业务超时等各种匪夷所思的现状。 于是SPM定位开始,OCM考试中SPM必考。 其他的AWR、ASH、SQLHC、SQLT、SQL profile等换作下一个话题…...

