当前位置：首页 > news >正文

华为OD机试 - 工号不够用了（Java） | 机试题+算法思路+考点+代码解析【2023】

news 2025/6/26 22:21:52

工号不够用了

3020年，空间通信集团的员工人数突破20亿人，即将遇到现有工号不够用的窘境。

现在，请你负责调研新工号系统。继承历史传统，新的工号系统由小写英文字母（a-z）和数字（0-9）两部分构成。新工号由一段英文字母开头，之后跟随一段数字，比如"aaahw0001",“a12345”,“abcd1”,“a00”。注意新工号不能全为字母或者数字,允许数字部分有前导0或者全为0。

但是过长的工号会增加同事们的记忆成本，现在给出新工号至少需要分配的人数X和新工号中字母的长度Y，求新工号中数字的最短长度Z。

输入输出描述:

输入描述:

一行两个非负整数 X Y，用数字用单个空格分隔。

0< X <=2^50 - 1
0< Y <=5

输出描述:

输出新工号中数字的最短长度Z

示例1

输入

260 1

输出

示例1

输入

2600 1

输出

解题思路

我们知道工号由于字符和数字组成，英文字母一起26个，数字字符一起有10个，y 来表示字符的长度，每个位置上都使用26个字母中任意一个，所以字符的可以表

华为OD机试 - 工号不够用了（Java） | 机试题+算法思路+考点+代码解析【2023】

工号不够用了 3020年，空间通信集团的员工人数突破20亿人，即将遇到现有工号不够用的窘境。现在，请你负责调研新工号系统。继承历史传统，新的工号系统由小写英文字母（a-z）和数字（0-9）两部分构成。新工号由一段英文字母开头，之后跟随一段数字，比如"aaahw0001&qu…...

编程日记 2023/2/23 23:34:40

Python学习-----lambda式匿名函数

目录前言： 1.什么是lambda函数 2.使用示例 （1）示例1：与def对比 （2）示例2：与三目运算符 （3）示例3：lambda作为参数传入其他函数 （4&#xff…...

编程日记 2023/2/23 23:33:33

华为OD机试真题Python实现【求解连续数列】真题+解题思路+代码（20222023）

求解连续数列题目已知连续正整数数列{K}=K1,K2,K3… Ki的各个数相加之和为S, i = N (0 < S < 100000, 0 < N < 100000), 求此数列K。 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试（Python）真题目录汇总 ## 输入输入包含两个参数连续正整数数…...

编程日记 2023/2/23 23:31:19

每日学术速递2.22

CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 Subjects: cs.CV 1.PriSTI: A Conditional Diffusion Framework for Spatiotemporal Imputation 标题：PriSTI：时空插补的条件扩散框架作者：Mingzhe Liu, Han Huan…...

编程日记 2023/2/23 23:30:12

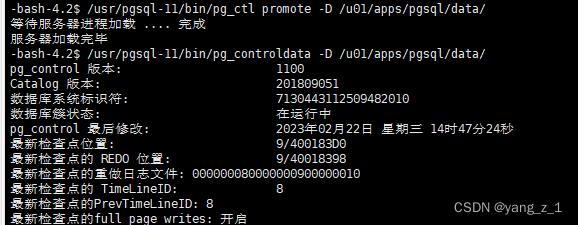
postgresql 数据库主从切换测试

postgresql 数据库主从切换测试文章目录postgresql 数据库主从切换测试前言环境：主从切换1. 查看数据库状态：2. 备库切换主库3. 旧主库切换成备库；4 查看状态后记前言因数据库等保需要，需要对老系统的数据库进行主从切换来…...

编程日记 2023/2/23 23:29:06

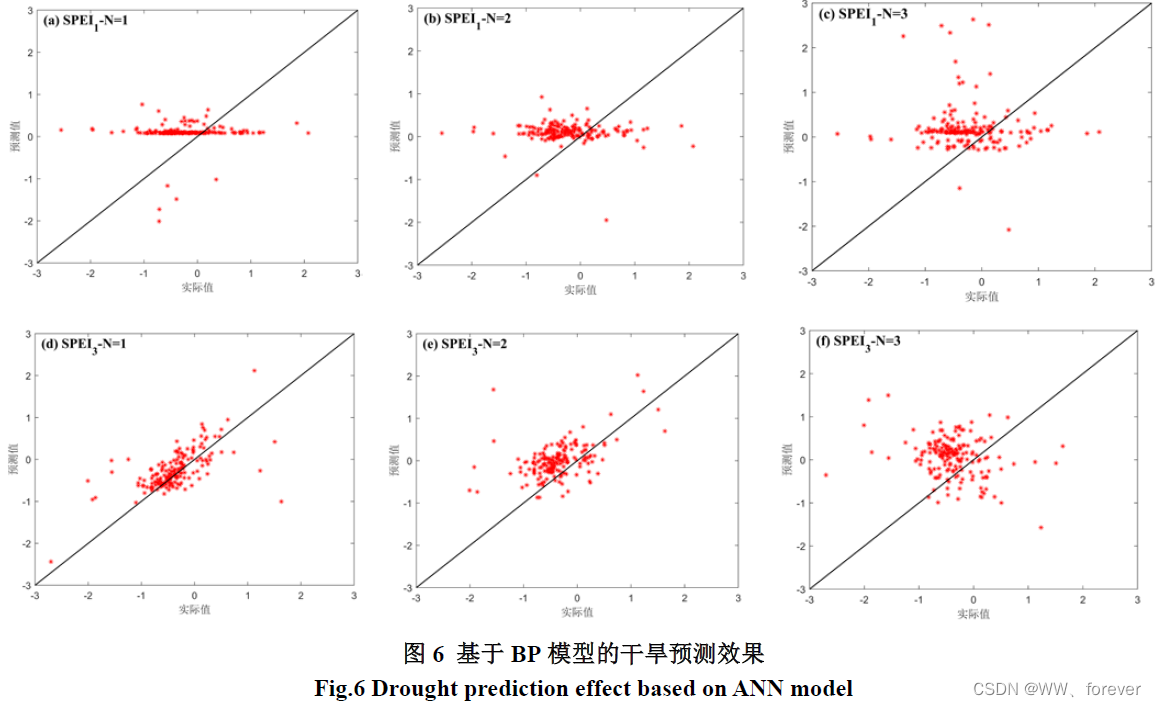
干旱预测方法总结及基于人工神经网络的干旱预测案例分析（MATLAB全代码）

本案例采用SPEI干旱指数，构建ANN和BP神经网络预测模型，并开展1~3个月预见期的干旱预测，对比分析干旱预测模型的适用性，为流域干旱预警和管理提供技术依据。干旱预测 1 干旱预测方法 1.1 统计学干旱预测根据历史降水或气温等…...

编程日记 2023/2/23 23:28:00

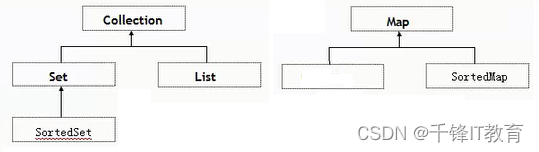
一篇文章弄清楚啥是数组和集合

数组和集合多语言都有，数组是集合的一种，是一种有序的集合，不面向对象，面向过程的也有。1.数组逻辑结构：线性的物理结构：顺序的存储结构申请内存：一次申请一大段连续的空间，一旦申请…...

编程日记 2023/2/23 23:26:54

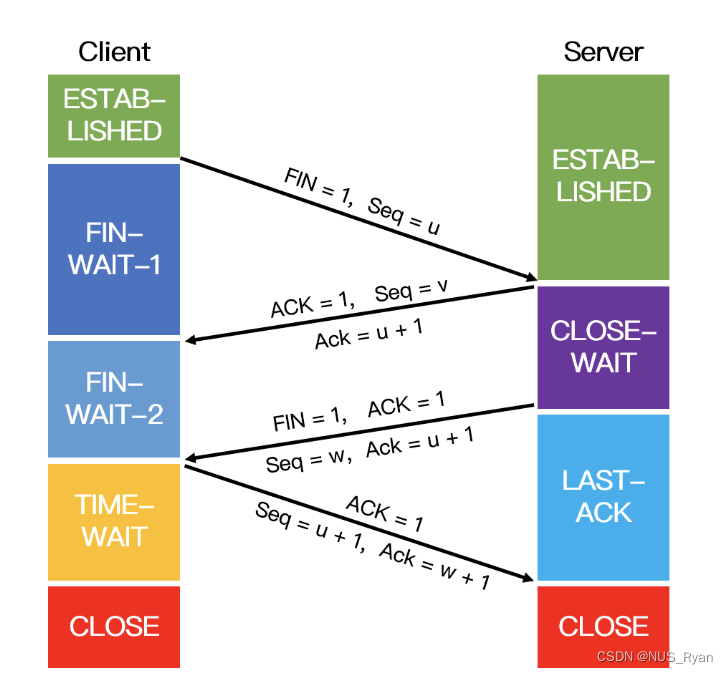
计算机网络(五):三次握手和四次挥手,TCP,UDP,TIME-WAIT,CLOSE-WAIT,拥塞避免，

文章目录零. TCP和UDP的区别以及TCP详解TCP是如何保证可靠性的TCP超时重传的原理TCP最大连接数限制TCP流量控制和拥塞控制流量控制拥塞控制TCP粘包问题一、三次握手和四次挥手二、为什么要进行三次握手？两次握手可以吗？三、为什么要进行四次挥手&#xf…...

编程日记 2023/2/23 23:25:48

【数据结构】二叉树(C语言实现)

文章目录一、树的概念及结构1.树的概念2.树的相关概念名词3.树的表示4.树在实际中的运用二、二叉树概念及结构1.二叉树的概念2.特殊的二叉树3.二叉树的性质4.二叉树的存储结构三、二叉树链式结构的实现1.结构的定义2.构建二叉树3.二叉树前序遍历4.二叉树中序遍历5.二叉树后序遍…...

编程日记 2023/2/23 23:24:40

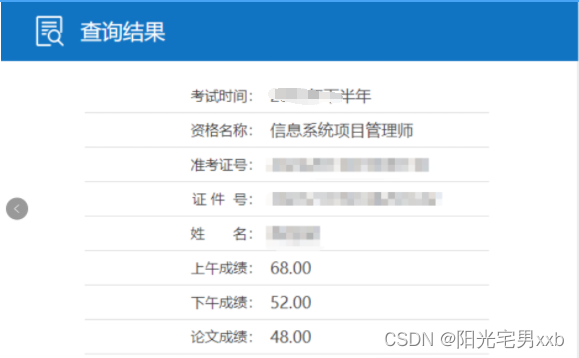
高级信息系统项目管理(高项软考)原创论文——成本管理（2）

1、如果您想了解如何高分通过高级信息系统项目管理师（高项）你可以点击链接：高级信息系统项目管理师（高项）高分通过经验分享_高项经验 2、如果您想了解更多的高级信息系统项目管理(高项软考)原创论文，您可以点击链接：...

编程日记 2023/2/23 23:23:34

代码签名即将迎来一波新关注

在数字化高度发展的当下，个人隐私及信息安全保护已经成了大家关注的重点，包括日常使用的电脑软件，手机APP等，由于包含了大量的用户信息，已经成了重点关注对象，任何一个疏忽就可能泄露大量用户信息。所以权威…...

编程日记 2023/2/23 23:22:27

黑盒渗透盲打lampiao

一、查找主机ip，通过Nmap扫描工具排查出我的靶机的IP 为.134 python tools.py ip -i 192.168.12.0 -h 254 -l 1 二、扫描其他端口。 1898 三、查看网站漏洞情况，典型的漏洞特征 Ac扫描漏洞情况，利用典型的漏洞。四、开始getshell 1、启动M…...

编程日记 2023/2/23 23:21:18

笔记：VLAN及交换机处理详细教程（Tagged, UnTagged and Native VLANS Tutorial）

一、内容来源本文是对下面这篇文章的总结，写的很全、很细致、干货满满，强力推荐： 《Tagged, UnTagged and Native VLANS Tutorial – A Quick Guide about What they Are?》二、为什么引入VLAN？ 早期设备间通过集线器&#x…...

编程日记 2023/2/23 23:20:12

在字节跳动，造赛博古籍

“你在字节跳动哪个业务？”“古籍数字化。把《论语》《左传》《道德经》这些古籍变成电子版，让大家都能免费看。”没错，除了你熟悉的那些 App，字节跳动还在做一些小众而特别的事情，古籍数字化就是其中之一。在字节跳动…...

编程日记 2023/2/23 23:19:05

Android 12.0设置默认Launcher安装一款Launcher默认Launcher无效的解决方案

1.概述在12.0的系统rom定制化过程中，在系统中当有多个Launcher的时候，这时候会要求设置默认Launcher,但是在最近的产品开发过程中，发现在设置完默认Launcher以后，在安装个Launcher的时候，会让原来设置的默认Launcher变为空了，就是在系统Settings中的默认应用中，launche…...

编程日记 2023/2/23 23:17:57

数据结构第16周：（希尔排序+ 堆排序 + 快速排序）

目录希尔排序堆排序快速排序希尔排序【问题描述】给出一组数据，请用希尔排序将其按照从小到大的顺序排列好。【输入形式】原始数据，以0作为输入的结束；第二行是增量的值，都只有3个。【输出形式】每一趟增量排序后的结果【…...

编程日记 2023/2/23 23:16:52

【C++】类和对象

1.面向过程和面向对象初步认识我们知道，C语言是面向过程的，关注的就是问题解决的过程； C是面向过程和面向对象混编，因为C兼容了C语言，而面向对象关注的不再是问题解决的过程； 而是一件事情所关联的不同…...

编程日记 2023/2/23 23:15:42

Java缓存面试题——Redis应用

文章目录1、为什么要使用Redis做缓存？2、为什么Redis单线程模型效率也能那么高？3、Redis6.0为什么要引入多线程呢？4、Redis常见数据结构以及使用场景字符串（String）哈希(Hash)列表（list）集合&am…...

编程日记 2023/2/23 23:14:34

KMP算法详细理解

一、目的1.KMP应用场景：可以解决字符串匹配问题； 在一个串中查找是否出现过另一个串。2.KMP的经典思想就是:当出现字符串不匹配时，可以记录一部分之前已经匹配的文本内容，利用这些信息避免从头再去做匹配。3.KMP算法关键在于&…...

编程日记 2023/2/23 23:13:28

RabbitMQ单节点安装

在学习RabbitMQ之前，必须要把RabbitMQ的环境搭建起来，刚开始学习时，搭建单节点是入门RabbitMQ最方便、最快捷的方式，这篇文章就是介绍如何使用RabbitMQ压缩包的方式搭建一个单节点的RabbitMQ。在实际项目中，服务器都…...

编程日记 2023/2/23 23:12:22

云原生核心技术 (7/12): K8s 核心概念白话解读(上)：Pod 和 Deployment 究竟是什么？

大家好，欢迎来到《云原生核心技术》系列的第七篇！ 在上一篇，我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在，我们就像一个拥有了一块崭新数字土地的农场主，是时…...

编程新知 2025/6/19 4:49:30

多模态2025：技术路线“神仙打架”，视频生成冲上云霄

文｜魏琳华编｜王一粟一场大会，聚集了中国多模态大模型的“半壁江山”。智源大会2025为期两天的论坛中，汇集了学界、创业公司和大厂等三方的热门选手，关于多模态的集中讨论达到了前所未有的热度。其中，…...

编程新知 2025/6/26 8:33:44

Java 语言特性(面试系列1)

一、面向对象编程 1. 封装（Encapsulation） 定义：将数据（属性）和操作数据的方法绑定在一起，通过访问控制符（private、protected、public）隐藏内部实现细节。示例： public …...

编程新知 2025/6/17 14:49:12

Go 语言接口详解

Go 语言接口详解核心概念接口定义在 Go 语言中，接口是一种抽象类型，它定义了一组方法的集合： // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的： // 矩形结构体…...

编程新知 2025/6/26 0:13:17

现代密码学 | 椭圆曲线密码学—附py代码

Elliptic Curve Cryptography 椭圆曲线密码学（ECC）是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。椭圆曲线密码学是多种数字签名算法的基础，例如椭圆曲线数字签…...

编程新知 2025/6/24 1:02:30

【OSG学习笔记】Day 16: 骨骼动画与蒙皮（osgAnimation）

骨骼动画基础骨骼动画是 3D 计算机图形中常用的技术，它通过以下两个主要组件实现角色动画。骨骼系统 (Skeleton)：由层级结构的骨头组成，类似于人体骨骼蒙皮 (Mesh Skinning)：将模型网格顶点绑定到骨骼上，使骨骼移动…...

编程新知 2025/6/24 2:02:57

OPenCV CUDA模块图像处理-----对图像执行均值漂移滤波（Mean Shift Filtering）函数meanShiftFiltering()

操作系统：ubuntu22.04 OpenCV版本：OpenCV4.9 IDE:Visual Studio Code 编程语言：C11 算法描述在 GPU 上对图像执行均值漂移滤波（Mean Shift Filtering），用于图像分割或平滑处理。该函数将输入图像中的…...

编程新知 2025/6/26 10:08:19

Docker 本地安装 mysql 数据库

Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ；并安装。基础操作不再赘述。打开 macOS 终端，开始 docker 安装mysql之旅第一步 docker search mysql 》〉docker search mysql NAME DE…...

编程新知 2025/6/22 5:30:42