[NOIP2002 普及组] 过河卒
题目描述:
棋盘上 A 点有一个过河卒,需要走到目标 B 点。卒行走的规则:可以向下、或者向右。同时在棋盘上 C 点有一个对方的马,该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。
棋盘用坐标表示,A 点 (0, 0)、B 点 (n, m),同样马的位置坐标是需要给出的。
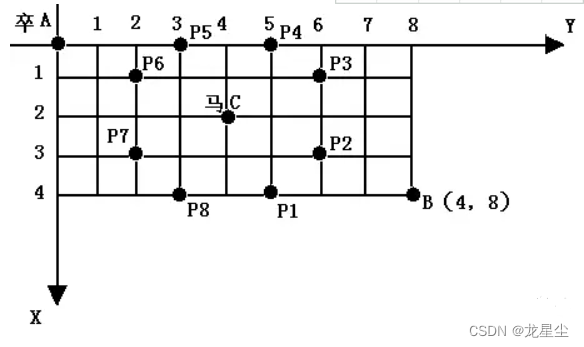
现在要求你计算出卒从 A 点能够到达 B 点的路径的条数,假设马的位置是固定不动的,并不是卒走一步马走一步。
输入格式:
一行四个正整数,分别表示 B 点坐标和马的坐标。
输出格式:
一个整数,表示所有的路径条数。
输入输出样例
输入 #1:
6 6 3 3
输出 #1:
6
说明/提示
对于 100% 的数据,1≤n,m≤20,0≤ 马的坐标≤20。
【题目来源】
NOIP 2002 普及组第四题
思路:
一道比较入门的 dp 题
这道题初始位置是从 0 开始的,这样不是很利于我们解题,所以不如暂且把这题里涉及的坐标统统 +1,那么初始位置就从 (0,0) 变成了 (1,1)。
先考虑如果没有任何马的限制,卒子可以随便向右向下走,那么可以想到,一个卒子只能从 当前格子的左侧格子 和 当前格子的上方格子 上走到当前格子。那么假设从 (1,1) 走到 当前格子的左侧格子 的路径条数是 x,从 (1,1) 走到 当前格子的上方格子 的路径条数是 y,那么从 (1,1) 走到当前格子的路径条数就应该是 x+y。
其实我们已经得到了一个动态规划的转移方程,设 f(i,j) 表示从 (1,1) 格子走到当前格子的路径条数,那么根据上一段得到的结论,可以得到:
f(i,j) = f(i-1,j) + f(i,j-1)
(i,j)是当前格子,那么 (i-1,j)就是 当前格子的上方格子,(i,j-1)就是 当前格子的左侧格子。我们只需要从小到大依次枚举 ii 和 jj 就能获得所有点的答案,可以想到,在这道题里我们要求的答案就是 f(n,m)(因为 B 点的坐标是(n,m)。
当然如果只是按照这个公式推肯定不行,因为 f 的初始数值都是 0,再怎么推也都是 0,我们要让 f(1,1)能根据上面得到的式子推出答案是 1,这样才能有有意义的结果。根据 f(1,1)=f(0,1)+f(1,0),我们只需要让 f(1,0)=1 或者 f(0,1)=1 即可。
接下来考虑一下加入了 马 这道题该怎么做,假设 (x,y) 这个点被马拦住了,其实就是说这个点不能被卒子走到,那当我们枚举到这个点的时候,发现他被马拦住了,那就直接跳过这个点,让 f(x,y)=0就行了。
具体写代码的时候我们注意到在判断一个点有没有被马拦住时,会用到 (i-2,j-1) 和 (i-1,j-2)这两个位置,那如果不把所有的点的坐标都加上 2 (前面分析的时候只把所有的坐标加上 1),就会因为数组越界而 WA 掉一个点。
答案可能很大,所以记得开 long long。
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#define ll long long
using namespace std;const int fx[] = {0, -2, -1, 1, 2, 2, 1, -1, -2};
const int fy[] = {0, 1, 2, 2, 1, -1, -2, -2, -1};
//马可以走到的位置int bx, by, mx, my;
ll f[40][40];
bool s[40][40]; //判断这个点有没有马拦住
int main(){scanf("%d%d%d%d", &bx, &by, &mx, &my);bx += 2; by += 2; mx += 2; my += 2;//坐标+2以防越界f[2][1] = 1;//初始化s[mx][my] = 1;//标记马的位置for(int i = 1; i <= 8; i++) s[mx + fx[i]][my + fy[i]] = 1;for(int i = 2; i <= bx; i++){for(int j = 2; j <= by; j++){if(s[i][j]) continue; // 如果被马拦住就直接跳过f[i][j] = f[i - 1][j] + f[i][j - 1];//状态转移方程}}printf("%lld\n", f[bx][by]);return 0;
} 考虑滚动数组优化。
观察转移方程:
f(i,j) = f(i - 1,j) + f(i,j - 1)
每一次转移只需要提供 f(i - 1,j)和 (,j - 1)。即当前位置上方格子的答案与当前位置左边的答案,也就是说,对于一次转移,我们只需要用到横坐标是 和横坐标是i- 1 这两行的答案,其他位置的答案已经是没有用处的了,我们可以直接丢掉不管他们。
怎么只保留第 i 行和第 - 1 行的答案呢? 答案是取模 (C++ 中的运算符 %) 。
%2( 1)% 2,所以我们把第一维的坐标都取模 2 变成% 2,并且不爱盖原来数组里存的答案,就成功做到只保留第 行和第 - 1 行的答案了
众所周知,2 % 2 可以在代码中写成更快的运算方式 i& 1如果 2 是偶,那么 2 & 1= 0,如果 是, 那么 2 & 1 = 1那么新的转移方程就可以变成:
f(0,1) = 1
f(i& 1,j)= f((- 1)& 1,j) + f(i& 1,j-1)f((i - 1) & 1,j)就是当前位置上边格子的答案f(i & 1j - 1)就是当前位置左边的答案
这样,数组第一维是不是就可以压成 2 了呢?
另外,因为是滚动数组,所以如果当前位置被马拦住了一定要记住清零。
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#define ll long long
using namespace std;const int fx[] = {0, -2, -1, 1, 2, 2, 1, -1, -2};
const int fy[] = {0, 1, 2, 2, 1, -1, -2, -2, -1};
int bx, by, mx, my;
ll f[2][40]; //第一维大小为 2 就好
bool s[40][40];int main(){scanf("%d%d%d%d", &bx, &by, &mx, &my);bx += 2; by += 2; mx += 2; my += 2;f[1][2] = 1; //初始化s[mx][my] = 1;for(int i = 1; i <= 8; i++) s[mx + fx[i]][my + fy[i]] = 1;for(int i = 2; i <= bx; i++){for(int j = 2; j <= by; j++){if(s[i][j]){f[i & 1][j] = 0; //被马拦住了记住清零continue;}f[i & 1][j] = f[(i - 1) & 1][j] + f[i & 1][j - 1]; //新的状态转移方程}}printf("%lld\n", f[bx & 1][by]);//输出的时候第一维也要按位与一下return 0;
} 好的那继续来看看能不能再优化。
唯一再有点优化空间的地方就是那个大小为 2 的第一维了,那么为什么我们去不掉这个 2 呢?
因为状态转移的时候需要一个 f(i-1,j),所以必须要多开一维。
那么我们如果优化掉了这里,当然就不再需要二维数组了。
观察我们能发现 , 这个 f(i-1,j) 与当前位置的 f(i,j)的第二维一样 , 都是 j , 而第一维只是差了 1。
我们考虑直接去掉第一维,来看这个状态转移方程 :
f(j) = f(j) + f(j-1)
是不是就把数组变成一维了呢?但是如何解释这个方程?
f(j)+f(j-1) 里面,f(j-1) 就是前面方程里的 f(i,j-1)。
至于 f(j), 因为还没有被更新过 , 所以答案仍然保存的是上次求出的答案 , 即 f(i−1,j)。
这样 , 就把二维数组成功变成了一维数组。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
using namespace std;// 快速读入
template <class I>
inline void read(I &num){num = 0; char c = getchar(), up = c;while(!isdigit(c)) up = c, c = getchar();while(isdigit(c)) num = (num << 1) + (num << 3) + (c ^ '0'), c = getchar();up == '-' ? num = -num : 0; return;
}
template <class I>
inline void read(I &a, I &b) {read(a); read(b);}
template <class I>
inline void read(I &a, I &b, I &c) {read(a); read(b); read(c);}const int fx[] = {0, -2, -1, 1, 2, 2, 1, -1, -2};
const int fy[] = {0, 1, 2, 2, 1, -1, -2, -2, -1};int bx, by, mx, my;
ll f[40]; //这次只需要一维数组啦
bool s[40][40];int main(){read(bx, by); read(mx, my);bx += 2; by += 2; mx += 2; my += 2;f[2] = 1; //初始化s[mx][my] = 1;for(int i = 1; i <= 8; i++) s[mx + fx[i]][my + fy[i]] = 1;for(int i = 2; i <= bx; i++){for(int j = 2; j <= by; j++){if(s[i][j]){f[j] = 0; // 还是别忘了清零continue;}f[j] += f[j - 1];//全新的 简洁的状态转移方程}}printf("%lld\n", f[by]);return 0;
} 这时可能就有同学说了,f 数组是变成一维了,但是你的 s 数组还是二维的啊你个骗子!
至于去掉 s 数组的方法,其实还是很多的。
首先有比较暴力的方法,我们直接去掉 s 数组,然后对于当前位置 (x,y),我们枚举被马拦住的那 8 个点,如果其中有一个点的位置和他的位置是一样的,那么这个位置就是不合法的了。这个方法可行,但是我们把本来是 O(n^2) 小常数的做法加了一个 8 倍常数。如果把范围开大到 n≤2×10^4,那么这个做法可能会被卡。
有没有别的方法呢?下面可能会用到这个知识点:切比雪夫距离。
我们注意到,被马拦住的位置到马的切比雪夫距离一定是2,也就是说,他们都分布于下图这个正方形上,那我们就成功缩小了枚举范围:只有当当前这个点 (x,y)(x,y) 到马的切比雪夫距离是 2 时,才进行 8 个点的枚举,那么复杂度大概就是 O(n^2+16×8)(原谅我用这种不正确的方法书写复杂度),常数很小。
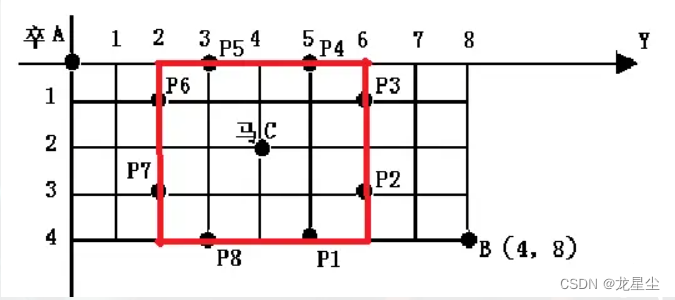
但是还能有更好的方法,那就是加上曼哈顿距离:我们可以发现,这些被马拦住的位置同时到马的曼哈顿距离也一定为 3。
蓝色是曼哈顿距离为 3 的位置,红色是切比雪夫距离为 2 的位置,交点是被马拦住的位置,且被马拦住的位置一定是交点,也就是说,这是个充要条件。
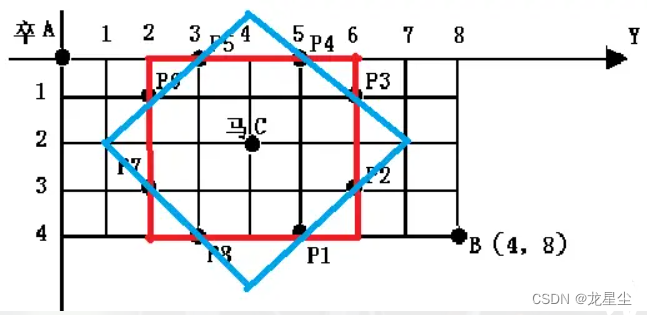
所以对于每个点我们只需要算一下他到马的切比雪夫距离和曼哈顿距离即可,这个计算都是 O(1)O(1) 的,且常数很小。
#include <cmath>
#include <cctype>
#include <cstdio>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#define ll long longinline int read(){int num = 0; char c = getchar();while(!isdigit(c)) c = getchar();while(isdigit(c)) num = (num << 1) + (num << 3) + (c ^ '0'), c = getchar();return num;
}int bx, by, mx, my;
ll f[30];inline bool check(int x, int y) {if(x == mx && y == my) return 1;return (std::abs(mx - x) + std::abs(my - y) == 3) && (std::max ((std::abs(mx - x)), std::abs(my - y)) == 2);
}int main(){bx = read() + 2, by = read() + 2, mx = read() + 2, my = read() + 2;f[2] = 1;for(int i = 2; i <= bx; i++){for(int j = 2; j <= by; j++){if(check(i, j)){f[j] = 0;continue;}f[j] += f[j - 1];}}printf("%lld\n", f[by]);return 0;
} 总结:
至此,我们成功将一个时间复杂度和空间复杂度为 O(n^2)O(n2) 的算法,优化到了时间复杂度 O(n^2)O(n2),空间复杂度 O(n)O(n),虽然对于这道题而言没有任何的意义,但是或许能在做其他难题的时候启发我们一点思路,总归是没有坏处的。
题目链接:
[NOIP2002 普及组] 过河卒 - 洛谷https://www.luogu.com.cn/problem/P1002
相关文章:

[NOIP2002 普及组] 过河卒
题目描述: 棋盘上 A 点有一个过河卒,需要走到目标 B 点。卒行走的规则:可以向下、或者向右。同时在棋盘上 C 点有一个对方的马,该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。 棋盘用坐标表…...
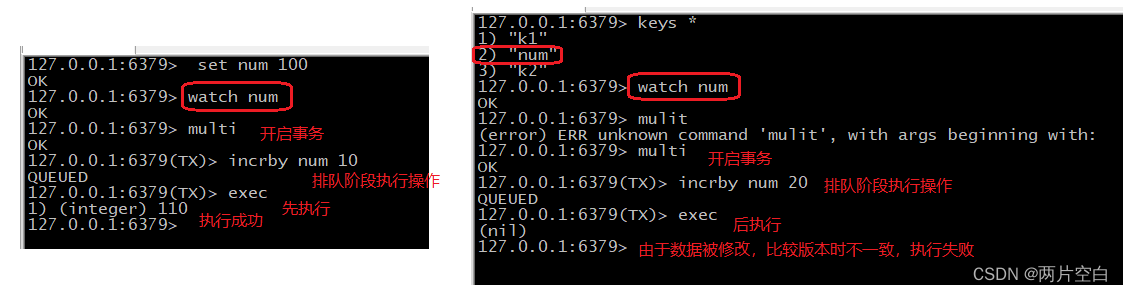
redis事务和锁机制
目录 事务定义 事务操作命令 redis事务的错误处理 redis事务冲突问题 redis解决事务冲突的方法 Redis事务的三个特性 事务定义 redis事务是一个单独的隔离操作:事务中的所有命令都会序列化,按顺序的执行。事务中在执行过程中,不会被其他客户…...

Java实例——线程
1、查看线程存活状态 Thread.isAlive() Thread.getName() public class MyThread extends Thread{Overridepublic void run() {for (int i 0; i < 10; i) {printMsg();}}public static void printMsg(){Thread thread Thread.currentThread();//Thread.getName() 获取线程…...

云计算学习课程——越来越重要的云安全
2023,越来越多的企业和组织正在或即将把核心系统和数据迁移上云端,其中以公有云和服务居多,那么就意味着在数据迁移的过程中会出现安全问题的几率更大。企业也越来越注重云安全体系,对我们云计算运维工程师来说,也是一…...
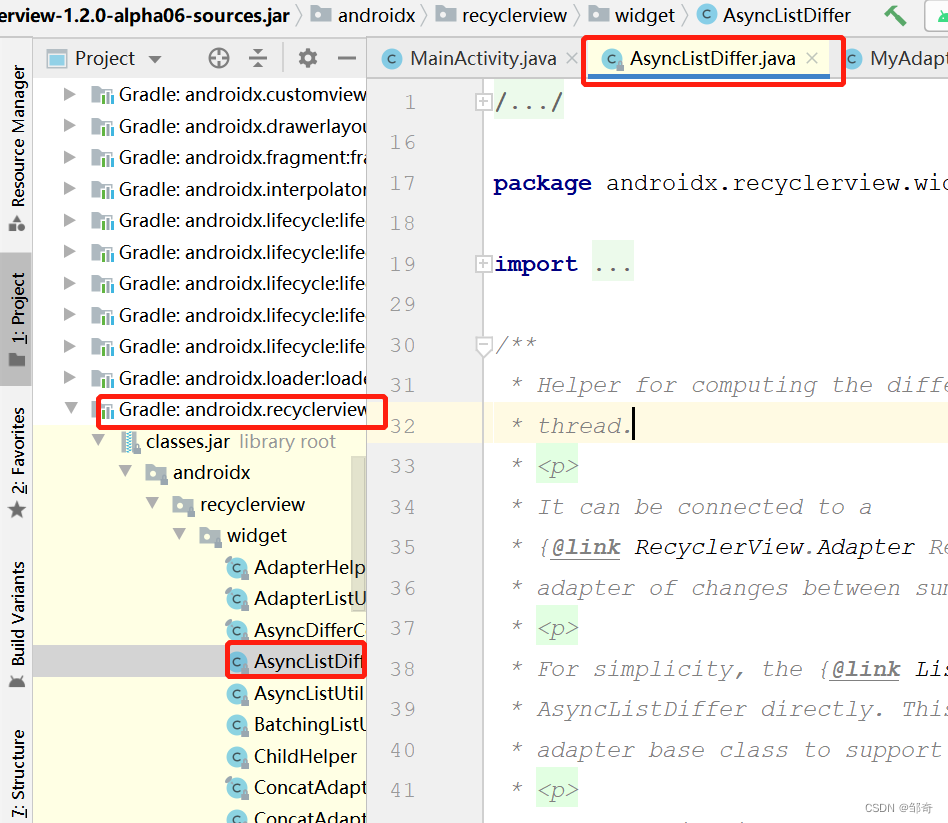
Android 高性能列表:RecyclerView + DiffUtil
文章目录背景介绍一般刷新 notifyDataSetChanged()局部刷新实现调用代码准备工作创建 MyDiffUtilCallback 类继承 DiffUtil.Callback 抽象类MyAdpter 类代码实现步骤总结通过 log 证实 diffutil 的局部刷新diffutil 优化后台线程参考主线程参考diff 更新优化后写法相关参考背景…...

为什么派生类的构造函数必须在初始化列表中调用基类的构造函数
调用派生类的构造函数时,可能会调用继承自基类的函数,也就可能会用到基类的数据成员,因此,调用派生类的构造函数时,必须确保继承自基类的数据成员已构造完毕,而将基类构造函数的调用写在初始化列表中&#…...

2023年2月初某企业网络工程师面试题【建议收藏】
拓扑图如下,主机A与主机B能互相通信,但是A不能ping通RA的F0接口,这是为什么?RA上f0接口上配置了ACL,禁止源ip为主机A,目的ip为RA f0的数据包的发送; 第一个路由器上只有到主机B网段的路由&#…...
单点登录)
分布式下(sso)单点登录
目录标题一、基于rediscookie的单点登录二、基于jwtcookie的单点登录一、基于rediscookie的单点登录 传统单机应用登录 传统单机应用,一般是结合session和cookie实现认证、授权。用户通过输入账号密码登录系统,登录成功后在系统创建一个session来保存用…...

PMP真的有那么厉害?你需要考PMP吗?
这个含金量是有的,是目前项目管理界含金量较高的证书,但也要分人, 因为这是职业证书,主要用于提高职场工作能力,不搞这一行的,PMP证书含金量再高也是一张废纸,可以看下下面这张图,这…...

高通平台开发系列讲解(WIFI篇)802.11 基本概念
文章目录 一、WLAN概述二、802.11发展历程三、802.11基本概念沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本文将基于高通平台介绍802.11基本概念。 一、WLAN概述 WLAN是Wireless Local Area Network的简称,指应用无线通信技术将计算机设备互联起来,构成可以互相通…...

扬帆优配|反弹涨超70%,昨收三连板,稀土行业或迎大事件
本年第一批稀土挖掘锻炼目标行将发放。 2月22日晚,东易日盛公告称,公司收到董事、副总经理兼财务总监李双侠出具的《关于未严格执行股份减持方案的致歉函》,其此次减持方案已施行结束,但在施行减持方案时,因操作失误&a…...
 | 机试题+算法思路+考点+代码解析 【2023】)
华为OD机试 - 工号不够用了(Java) | 机试题+算法思路+考点+代码解析 【2023】
工号不够用了 3020年,空间通信集团的员工人数突破20亿人,即将遇到现有工号不够用的窘境。 现在,请你负责调研新工号系统。继承历史传统,新的工号系统由小写英文字母(a-z)和数字(0-9)两部分构成。新工号由一段英文字母开头,之后跟随一段数字,比如"aaahw0001&qu…...

Python学习-----lambda式匿名函数
目录 前言: 1.什么是lambda函数 2.使用示例 (1)示例1:与def对比 (2)示例2:与三目运算符 (3)示例3:lambda作为参数传入其他函数 (4ÿ…...
)
华为OD机试真题Python实现【求解连续数列】真题+解题思路+代码(20222023)
求解连续数列 题目 已知连续正整数数列{K}=K1,K2,K3… Ki的各个数相加之和为S, i = N (0 < S < 100000, 0 < N < 100000), 求此数列K。 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Python)真题目录汇总 ## 输入 输入包含两个参数 连续正整数数…...

每日学术速递2.22
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 Subjects: cs.CV 1.PriSTI: A Conditional Diffusion Framework for Spatiotemporal Imputation 标题:PriSTI:时空插补的条件扩散框架 作者:Mingzhe Liu, Han Huan…...
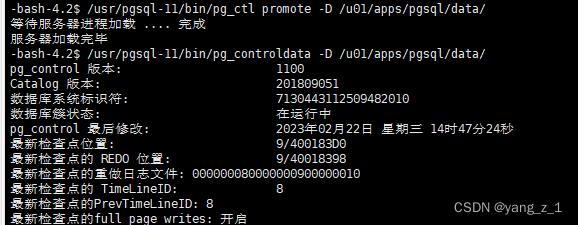
postgresql 数据库 主从切换 测试
postgresql 数据库 主从切换 测试 文章目录postgresql 数据库 主从切换 测试前言环境:主从切换1. 查看数据库状态:2. 备库切换主库3. 旧主库切换成备库;4 查看状态后记前言 因数据库等保需要,需要对老系统的数据库进行主从切换来…...
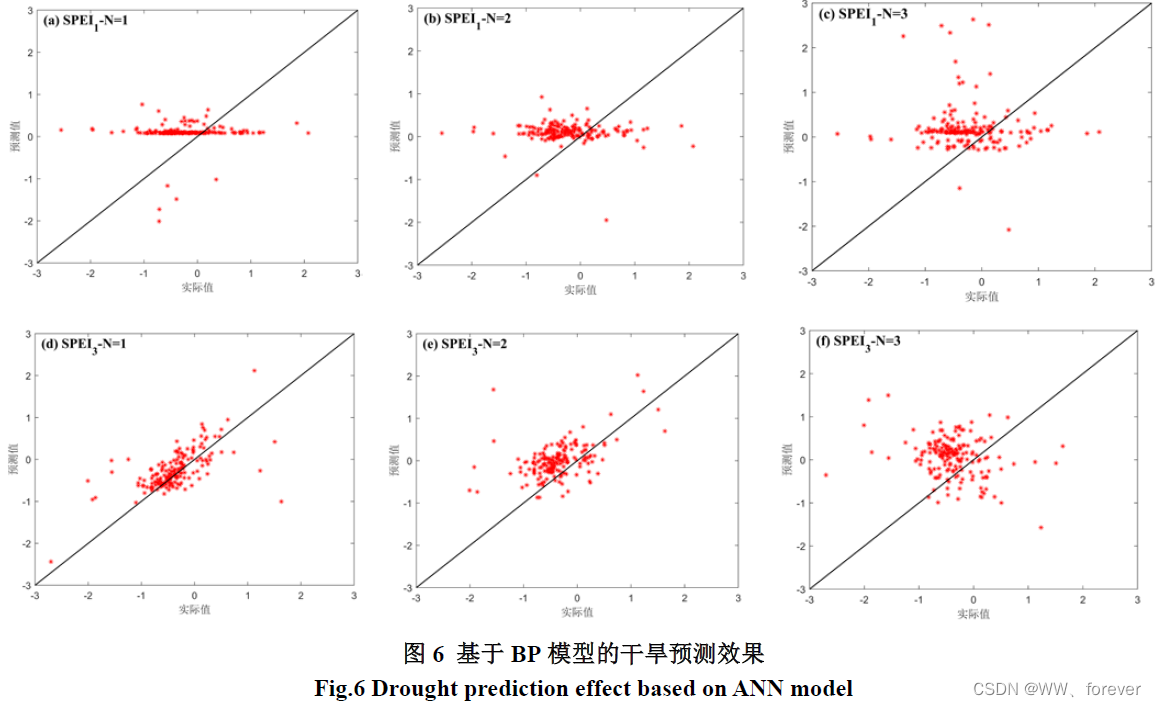
干旱预测方法总结及基于人工神经网络的干旱预测案例分析(MATLAB全代码)
本案例采用SPEI干旱指数,构建ANN和BP神经网络预测模型,并开展1~3个月预见期的干旱预测,对比分析干旱预测模型的适用性,为流域干旱预警和管理提供技术依据。 干旱预测 1 干旱预测方法 1.1 统计学干旱预测 根据历史降水或气温等…...
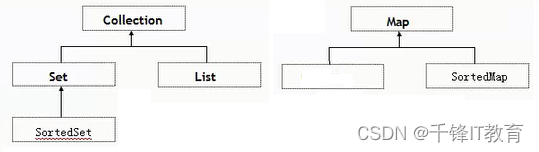
一篇文章弄清楚啥是数组和集合
数组和集合多语言都有,数组是集合的一种,是一种有序的集合,不面向对象,面向过程的也有。1.数组逻辑结构:线性的物理结构:顺序的存储结构申请内存:一次申请一大段连续的空间,一旦申请…...
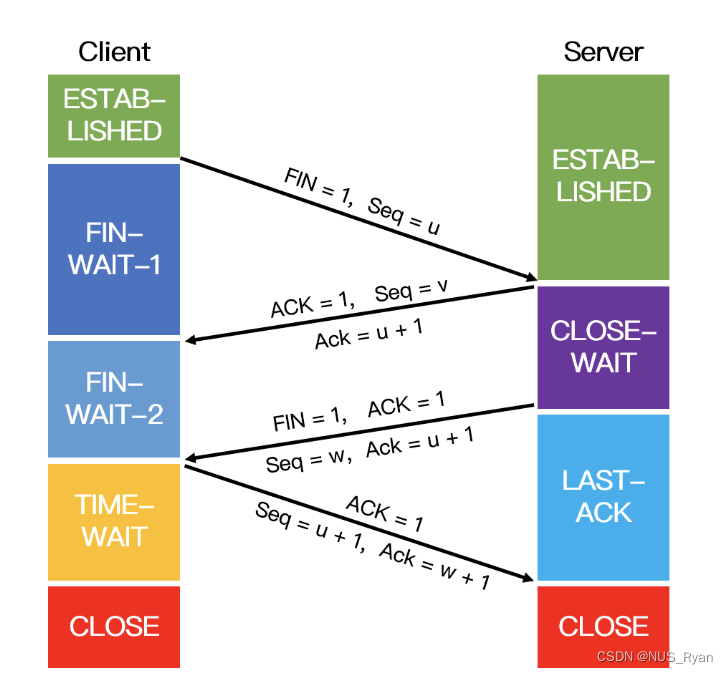
计算机网络(五):三次握手和四次挥手,TCP,UDP,TIME-WAIT,CLOSE-WAIT,拥塞避免,
文章目录零. TCP和UDP的区别以及TCP详解TCP是如何保证可靠性的TCP超时重传的原理TCP最大连接数限制TCP流量控制和拥塞控制流量控制拥塞控制TCP粘包问题一、三次握手和四次挥手二、为什么要进行三次握手?两次握手可以吗?三、为什么要进行四次挥手…...

【数据结构】二叉树(C语言实现)
文章目录一、树的概念及结构1.树的概念2.树的相关概念名词3.树的表示4.树在实际中的运用二、二叉树概念及结构1.二叉树的概念2.特殊的二叉树3.二叉树的性质4.二叉树的存储结构三、二叉树链式结构的实现1.结构的定义2.构建二叉树3.二叉树前序遍历4.二叉树中序遍历5.二叉树后序遍…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...
