二刷力扣--二叉树(2)
226.翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
使用递归解决。
- 确定函数参数和返回值
函数参数为当前节点cur。无返回值。
def dd(cur):
- 确定终止条件。当前节点为空则终止。
if not cur:return
- 单层逻辑
反转当前节点的左右,然后递归调用cur.left, cur.right
def dd(cur):if not cur:return cur.left, cur.right = cur.right, cur.leftdd(cur.left)dd(cur.right)
完整代码如下:
class Solution:def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:def dd(cur):if not cur:return cur.left, cur.right = cur.right, cur.leftdd(cur.left)dd(cur.right)dd(root)return root
101.对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
这题用层序遍历很好做,只要判断每层是不是对称的就好了(空的节点添加一个特殊值方便判断对称)。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution: def isSymmetric(self, root: Optional[TreeNode]) -> bool:def symmetric_list(lst):length = len(lst)i = 0j = length-1while i < j:if lst[i] != lst[j]:return Falsei += 1j -= 1return Trueres = []if not root:return resqueue = deque()queue.append(root)while len(queue) > 0:next_list = []length = len(queue)for i in range(length):node = queue.popleft()if node.left:queue.append(node.left)next_list.append(node.left.val)else:next_list.append(-9999)if node.right:queue.append(node.right)next_list.append(node.right.val)else:next_list.append(-9999)if not symmetric_list(next_list):return Falsereturn True
递归方式有点绕,因为要判断的是轴对称。
- 函数参数和返回值。
参数是左子节点和右子节点。返回值是 bool值,表示是否当前节点是否轴对称。
def compare(left, right):
- 终止条件。
左右节点全为空或某个为空时,则可以判断出当前节点的左右是否是对称的了。
if not left and not right:return True
elif not left or not right:return False
- 单层逻辑
return left.val == right.val and \compare(left.left, right.right) and compare(left.right, right.left)
104.二叉树的最大深度
给定一个二叉树 root ,返回其最大深度。
层序遍历非常直接,遍历的层数就是深度。
class Solution:def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:res = []if not root:return resqueue = deque()queue.append(root)while len(queue) > 0:sub_list = []length = len(queue) # 注意for i in range(length):node = queue.popleft()sub_list.append(node.val)if node.left:queue.append(node.left)if node.right:queue.append(node.right)res.append(sub_list)return resdef maxDepth(self, root: Optional[TreeNode]) -> int:res = self.levelOrder(root)return len(res)
递归更简单:
- 函数参数和返回值。
参数为当前节点node。返回值为int值,表示节点的深度。 - 终止条件
节点为空时,返回0. - 单层逻辑
max(左节点深度,右节点深度) +1
class Solution:def maxDepth(self, root: Optional[TreeNode]) -> int:def depth(node):if not node:return 0leftDepth = depth(node.left)rightDepth = depth(node.right)return max(leftDepth, rightDepth)+1return depth(root)
- 二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数。
- 二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数。
本题可以使用前序遍历(中左右),也可以使用后序遍历(左右中),使用前序求的就是深度,使用后序求的是高度。
而根节点的高度就是二叉树的最大深度,所以本题中我们通过后序求的根节点高度来求的二叉树最大深度。
111.二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
这题层序遍历还是很简单,因为每遍历一层就对应深度+1。如果找到了叶子节点就可以终止遍历返回当前深度了。
class Solution:def minDepth(self, root: Optional[TreeNode]) -> int:if not root:return 0queue = deque()queue.append(root)depth = 0while queue:depth += 1length = len(queue)for i in range(length):node = queue.popleft()if all([not node.left, not node.right]):return depth for nextnode in [node.left, node.right]:if nextnode:queue.append(nextnode)return depth
递归方式。
递归方式和104求最大深度差很多。最小深度必须是根节点到叶子节点的长度,如果左子树为空,右子树不为空,则只能通过右子树到达叶子节点(1+rightDepth)。
递归公式:
- 函数参数和返回值。
参数为当前节点node。返回值为int值,表示节点的深度。 - 终止条件
节点为空时,返回0. - 单层逻辑
如果只有右子树,返回 1+rightDepth
如果只有左子树,返回 1+leftDepth
否则,返回 min(左节点深度,右节点深度) +1
class Solution:def minDepth(self, root: Optional[TreeNode]) -> int:def getDepth(node: Optional[TreeNode]) -> int:if not node :return 0leftDepth = getDepth(node.left)rightDepth = getDepth(node.right)if not node.left and node.right :return 1+ rightDepthif not node.right and node.left:return 1+ leftDepthreturn 1 + min(leftDepth, rightDepth)return getDepth(root)
222.完全二叉树的节点个数
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
遍历一次就知道节点个数了。
但是这样就没有用到完全二叉树的性质。
完全二叉树只有两种情况,情况一:就是满二叉树,情况二:最后一层叶子节点没有满。
对于情况一,可以直接用 2^树深度 - 1 来计算,注意这里根节点深度为1。
对于情况二,分别递归左孩子,和右孩子,递归到某一深度一定会有左孩子或者右孩子为满二叉树,然后依然可以按照情况1来计算。
递归公式:
-
函数参数和返回值。
参数是当前节点。返回值是当前节点为根节点的树的节点个数。 -
终止条件
如果节点为None,返回0。 -
单层逻辑
判断当前节点是不是满二叉树,是满二叉树则直接用公式2^树深度 - 1返回节点数。否则递归处理左右子树,返回左子树节点数 + 右子树节点数 + 1。
class Solution:def countNodes(self, root: Optional[TreeNode]) -> int:if not root:return 0# 判断当前节点是不是满二叉树leftHeight, rightHeight = 0, 0left, right = root.left, root.rightwhile left:left = left.leftleftHeight += 1while right:right = right.rightrightHeight += 1# 是满二叉树,则用公式计算if leftHeight == rightHeight:return (2 << leftHeight) -1# 否则递归处理left, rightreturn self.countNodes(root.left) + self.countNodes(root.right) + 1
110.平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。
一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1 。
- 二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数。
- 二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数。
LeetCode上的不是按照路径数,而是按照节点数计算。
求深度可以从上到下去查 所以需要前序遍历(中左右),而高度只能从下到上去查,所以只能后序遍历(左右中)。
递归公式
- 函数参数和返回值
参数为当前节点,返回值为节点的高度。返回值为-1时表示不是平衡二叉树。 - 终止条件
节点为None,返回0。 - 单层逻辑
求左子树高度,如果为-1,则已经不平衡了,返回-1.
求右子树高度,如果为-1,则已经不平衡了,返回-1.
如果左右子树高度差>1,不平衡,返回-1.
否则返回当前节点的高度,1 + max(leftDepth, rightDepth)
class Solution:def isBalanced(self, root: Optional[TreeNode]) -> bool:def getHeight(node):if not node:return 0leftDepth = getHeight(node.left)if leftDepth == -1: return -1rightDepth = getHeight(node.right)if rightDepth == -1: return -1if abs(leftDepth - rightDepth) > 1:return -1else:return 1 + max(leftDepth, rightDepth)return not getHeight(root) == -1
257.二叉树的所有路径
按 任意顺序 ,返回所有从根节点到叶子节点的路径。
递归+回溯。
递归公式
- 参数和返回值
参数是当前节点、路径、(存放结果的数组)。返回值无。 - 终止条件
到达叶子节点。 - 单层逻辑
添加当前节点,递归(+回溯)遍历左子树和右子树。
class Solution:def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:def traversal(cur, path, result):path.append(cur.val) # 终止条件:到达叶子节点了 if not any([cur.left, cur.right]):sPath = ""for n in path:sPath += str(n)sPath += "->"sPath = sPath[:-2]result.append(sPath)return# 左子树 if cur.left:traversal(cur.left, path, result)path.pop() # 回溯# 右子树 if cur.right:traversal(cur.right, path, result)path.pop()result = []path = []if not root:return resulttraversal(root, path, result)return result
404.左叶子之和
给定二叉树的根节点 root ,返回所有左叶子之和。
左叶子:是父节点的左节点,并且是叶子节点。
递归公式:
- 函数参数和返回值
参数是当前节点,返回值是当前节点的左叶子之和。 - 终止条件
当前节点为None,返回0. - 单层逻辑
如果当前节点是左叶子,则要加入当前节点的值。然后加上左子树的左叶子和,右子树的左叶子和。
class Solution:def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:def getLeft(node):if not node:return 0leftValue = getLeft(node.left)rightValue = getLeft(node.right)midValue = 0# 左叶子:# 它是父节点的左节点,同时它是叶子节点if node.left and node.left.left == None and node.left.right ==None:midValue = node.left.val return midValue + leftValue + rightValuereturn getLeft(root)
513.找树左下角的值
给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。
层序遍历比较简单,遍历完然后获取最后一层的第一个节点。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:res = []if not root:return resqueue = deque()queue.append(root)while queue:sub_list = []length = len(queue)for i in range(length):node = queue.popleft()sub_list.append(node.val)for nextnode in [node.left, node.right]:if nextnode:queue.append(nextnode)res.append(sub_list)return resdef findBottomLeftValue(self, root: Optional[TreeNode]) -> int:return self.levelOrder(root)[-1][0]
递归方式。
递归找最底层最左的节点,需要知道层数。
递归公式:
- 函数参数和返回值。
参数是当前节点和当前层数。 - 终止条件
到达叶子节点。 - 单层逻辑
递归处理左子树和右子树,深度+1.
class Solution:def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:maxDepth = -11111 # 最大深度maxLeftValue = 0 # 最深层 最左的节点值def traversal(root, depth):nonlocal maxDepth, maxLeftValue# 终止条件: 到达叶子if not root.left and not root.right:# 深度是最深的,更新答案if depth > maxDepth:maxDepth = depthmaxLeftValue = root.valreturn# 递归处理左右if root.left:traversal(root.left, depth+1) # 隐藏回溯if root.right:traversal(root.right, depth+1)return traversal(root,0)return maxLeftValue
112.路径总和
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
递归公式:
- 函数参数和返回值
参数:当前节点root,目标和targetSum。
返回值:bool值,表示是否满足题目要求。 - 终止条件:
当前节点为None,返回False - 单层逻辑:
如果是叶子节点,判断当前值和目标值是否相等。
否则对左、右子数递归判断。
class Solution:def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:if not root:return Falseif not root.left and not root.right:return root.val == targetSumreturn self.hasPathSum(root.left, targetSum-root.val) or self.hasPathSum(root.right, targetSum-root.val)
相关文章:
)
二刷力扣--二叉树(2)
226.翻转二叉树 给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。 使用递归解决。 确定函数参数和返回值 函数参数为当前节点cur。无返回值。 def dd(cur):确定终止条件。当前节点为空则终止。 if not cur:return 单层逻辑 反转当前…...

【C++ Efficiency】使用运算符的复合形式取代其单独形式,效率更高
//单独形式 x x y; x x - y; //也可以写为复合形式 x y; x - y;效率问题 一般而言,复合操作符比其对应的单独形式效率高:因为单独形式需要返回一个新的对象,就会产生一个临时对象的构造和析构成本,复合版本则是直接写入左…...

uview的真机演示,微信小程序,当两个input框的时候,从一个input切换到两一个input的时候,键盘调不起来
项目场景: 项目相关背景: 例如:uview的真机演示,微信小程序,当两个input框的时候,从一个input切换到两一个input的时候,键盘调不起来 问题描述 遇到的问题: 例如:切…...

信息化发展58
安全系统 X 轴是“ 安全机制” 。安全机制可以理解为提供某些安全服务, 利用各种安全技术和技巧, 所形成的一个较为完善的结构体系。如“ 平台安全” 机制, 实际上就是指安全操作系统、安全数据库、应用开发运营的安全平台以及网络安全管理监…...

2023前端面试题
一.HTML篇 1.HTML是什么?它的缩写代表什么? HTML代表"超文本标记语言"(Hypertext Markup Language),它是一种用于创建网页结构和内容的标记语言。 2.HTML文档的基本结构是什么? 基本的HTML结构包…...
Spring整合第三方框架-MyBatis原始操作代码
建议自己写一下 实体类,用于封装数据库数据 package com.example.pojo;import java.util.Date;public class Emp {private Integer id;private String username;private String password;private String name;private Integer gender;private String image;privat…...

比特币 ZK 赏金系列:第 2 部分——查找哈希冲突
在我们的零知识赏金 (ZKB) 系列的第二部分中,我们将其应用于解决哈希冲突难题。在这样的谜题中,两个不同的输入散列到相同的输出。此类赏金可用于: 充当煤矿中的金丝雀,给我们一个有价值的提醒。存在冲突是散列函数较弱的标志&…...

Android9底部导航栏出现空白按钮问题分析
Android9底部导航栏出现空白按钮问题分析 底部导航栏的初始化 进入NavigationBarView初始化: 进入NavigationBarView的onFinishInflater进入NavigationBarInflaterView NavigationBarInflaterView加载单个的button回到NavigationFragment的创建流程 多次调用NavigationBarView的…...
秦时明月沧海手游阵容推荐,秦时明月沧海角色强度
秦时明月沧海角色强度如何?在秦时明月沧海手游中,您可以从大量的角色卡牌中选择并发展,为了顺利通过各种副本,玩家们需要精心搭配阵容。那么,具体该如何配置最强的角色呢? 下面,小编将带各位玩家…...

基于微信小程序的大学生科技竞赛竞技报名系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言系统主要功能:具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计…...
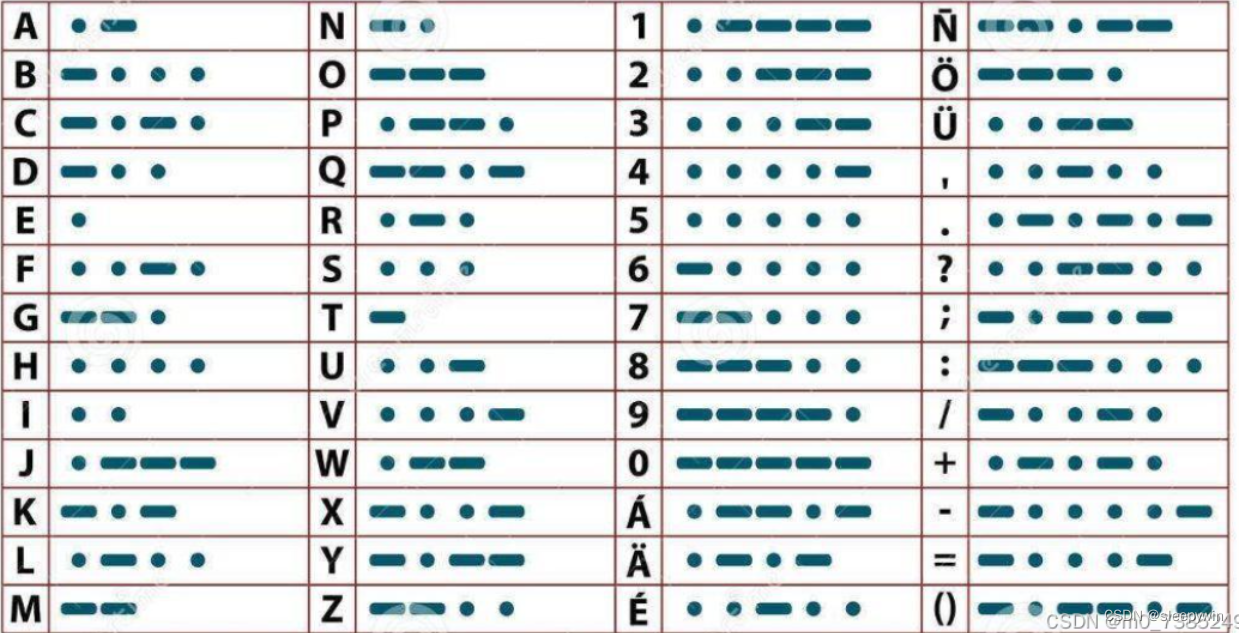
crypto:摩丝
题目 根据题目所给的压缩包下载后解压,打开文本提示 摩斯密码,对照表可解码得到flag...

Docker最基本使用
1 安装: sudo apt-get -y install docker.io测试: sudo docker run hello-world成功: Hello from Docker! This message shows that your installation appears to be working correctly.2 查看 查看已有镜像: sudo docker i…...
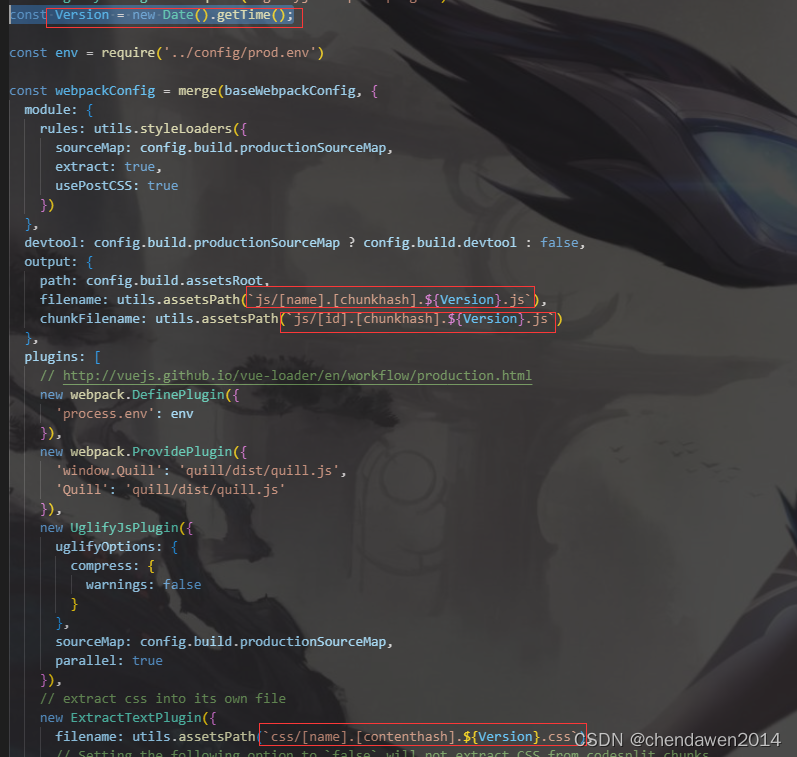
vue2.x 迭代更新项目去掉缓存处理
找到build文件下的webpack.prod.conf.js文件 定义一个常量version const Version new Date().getTime(); 然后在.js和.css前面加上.${Version}就可以了(注意得把原本的换成)...
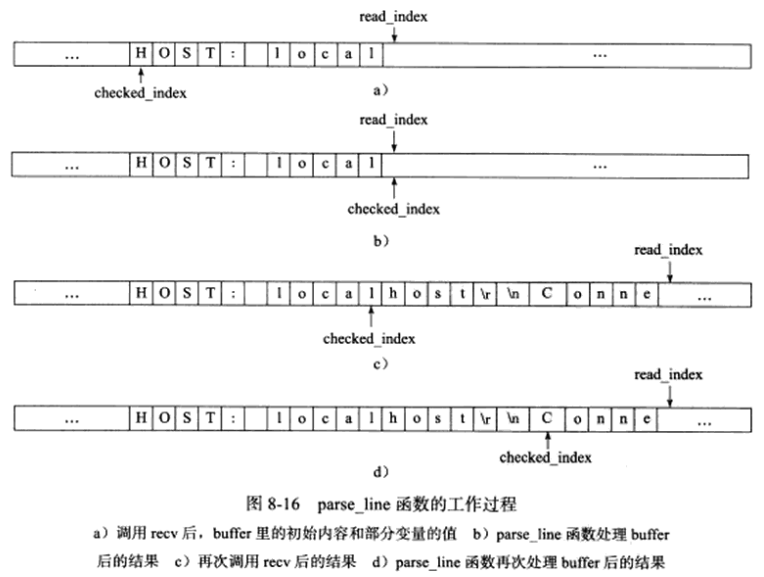
Linux高性能服务器编程 学习笔记 第八章 高性能服务器程序框架
TCP/IP协议在设计和实现上没有客户端和服务器的概念,在通信过程中所有机器都是对等的。但由于资源(视频、新闻、软件等)被数据提供者所垄断,所以几乎所有网络应用程序都采用了下图所示的C/S(客户端/服务器)…...

技术对比:Flutter vs. 传统桌面应用开发框架
在移动应用开发领域,Flutter已经赢得了广泛的认可和采用,成为了跨平台移动应用开发的瑞士军刀。然而,Flutter的魅力并不仅限于移动平台,它还可以用于开发桌面应用程序,为开发人员提供了一种全新的选择。本文将深入探讨…...
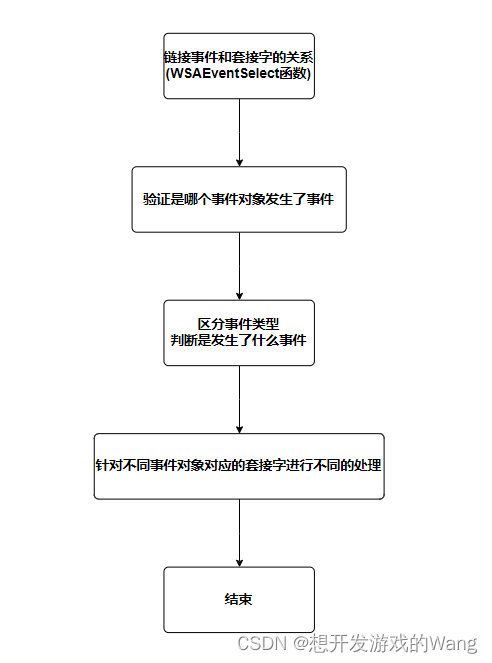
[C++ 网络协议] 异步通知I/O模型
1.什么是异步通知I/O模型 如图是同步I/O函数的调用时间流: 如图是异步I/O函数的调用时间流: 可以看出,同异步的差别主要是在时间流上的不一致。select属于同步I/O模型。epoll不确定是不是属于异步I/O模型,这个在概念上有些混乱&a…...

Postgresql事务测试
参考一个事务中 可以查询自己未提交的数据吗_最详细MySQL事务隔离级别及原理讲解!(二)-CSDN博客 一个事务中 可以查询自己未提交的数据吗_趣说数据库事务隔离级别与原理_weixin_39747293的博客-CSDN博客 【MySql:当前读与快照读…...
【数据结构--排序】冒泡排序,选择排序,插入排序
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃个人主页 :阿然成长日记 …...

vue pc端/手机移动端 — 下载导出当前表格页面pdf格式
一、需求:在手机端/pc端实现一个表格页面(缴费单/体检报告单等)的导出功能,便于用户在本地浏览打印。 二、实现:之前在pc端做过预览打印的功能,使用的是print.js之类的方法让当前页面直接唤起打印机的打印预…...

125. 验证回文串 【简单题】
题目 如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后,短语正着读和反着读都一样。则可以认为该短语是一个 回文串 。 字母和数字都属于字母数字字符。 给你一个字符串 s,如果它是 回文串 ,返回 true ;否则…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...
