信息论基础第二章阅读笔记
信息很难用一个简单的定义准确把握。
对于任何一个概率分布,可以定义一个熵(entropy)的量,它具有许多特性符合度量信息的直观要求。这个概念可以推广到互信息(mutual information),互信息是一种测度,用来度量一个随机变量包含另一个随机变量的信息量。熵恰好变成一个随机变量的自信息。相对熵(relative entropy)是个更广泛的量,它是刻画两个概率分布之间的距离的一种度量,而互信息又是它的特殊情形。
相对熵(也叫做KL散度)、互信息和熵都是信息理论中的重要概念,它们之间有一定的关系,我会尽量用通俗易懂的方式解释它们之间的关系。
- 熵(Entropy):想象一堆信息,如果这些信息非常混乱和不可预测,那么熵就高。相反,如果信息有序和高度可预测,熵就低。熵用来衡量一个随机变量的不确定性。在信息理论中,熵通常用H表示,表示一个随机事件中信息的平均不确定性。如果一个事件的概率分布是均匀的,那么熵最高;如果概率分布是确定的,熵为零。
- 相对熵(Kullback-Leibler Divergence,KL散度):相对熵用来衡量两个概率分布之间的差异。具体来说,如果我们有两个概率分布P和Q,相对熵D(P || Q)用来表示当我们使用Q来近似描述P时所带来的信息损失。如果P和Q完全相同,相对熵为零,表示没有信息损失。但如果它们不同,相对熵就会大于零,表示用Q来近似P会引入一些误差。
- 互信息(Mutual Information):互信息用来衡量两个随机变量之间的关联性。如果我们有两个随机变量X和Y,它们的互信息I(X; Y)表示知道了一个变量的值后,对另一个变量的不确定性的减少程度。互信息越大,表示X和Y之间的关联性越强。如果X和Y是完全独立的,互信息为零,表示它们之间没有关联。
现在来解释它们之间的关系:
- 相对熵可以用来衡量两个概率分布的差异,它可以用来衡量一个概率分布Q对另一个分布P的逼近程度。
- 互信息可以用来衡量两个随机变量之间的关联性,它可以看作是一个随机变量X和Y的联合分布与它们各自的分布之间的相对熵之和减去它们的联合分布的相对熵。具体而言, I ( X ; Y ) = D ( P ( X , Y ) ∣ ∣ P ( X ) P ( Y ) ) I(X; Y) = D(P(X, Y) || P(X)P(Y)) I(X;Y)=D(P(X,Y)∣∣P(X)P(Y))。
总之,这些概念在信息论和统计学中有广泛的应用,用来量化信息、概率分布之间的关系以及随机变量之间的关联性。相对熵和互信息都是用来衡量信息的不同方面,而熵则是其中一个基础概念,用来衡量不确定性。
当谈到相对熵(KL散度)、互信息和熵时,以下是它们的公式表示:
- 熵(Entropy):熵用H表示,对于一个随机变量X,它的熵H(X)可以表示为:
H ( X ) = − ∑ x P ( x ) log P ( x ) H(X) = -\sum_{x} P(x) \log P(x) H(X)=−x∑P(x)logP(x)
这里,P(x)是随机变量X取某个值x的概率,\log表示自然对数。- 相对熵(Kullback-Leibler Divergence,KL散度):对于两个概率分布P和Q,它们之间的相对熵D(P || Q)可以表示为:
D ( P ∣ ∣ Q ) = ∑ x P ( x ) log ( P ( x ) Q ( x ) ) D(P || Q) = \sum_{x} P(x) \log\left(\frac{P(x)}{Q(x)}\right) D(P∣∣Q)=x∑P(x)log(Q(x)P(x))
这个公式用来衡量P和Q之间的差异。- 互信息(Mutual Information):对于两个随机变量X和Y,它们的互信息I(X; Y)可以表示为:
I ( X ; Y ) = ∑ x , y P ( x , y ) log ( P ( x , y ) P ( x ) P ( y ) ) I(X; Y) = \sum_{x, y} P(x, y) \log\left(\frac{P(x, y)}{P(x)P(y)}\right) I(X;Y)=x,y∑P(x,y)log(P(x)P(y)P(x,y))
这个公式用来衡量X和Y之间的关联性。需要注意的是,相对熵和互信息的公式都包括对概率分布的取值进行求和,而熵的公式只涉及一个随机变量的概率分布。这些公式在信息理论和统计学中有广泛的应用,用来量化信息、概率分布之间的关系以及随机变量之间的关联性。
2.1 熵
2.2联合熵与条件熵
2.3相对熵与互信息
2.4熵与互信息的关系
2.5熵、相对熵与互信息的链式法则
2.6Jensen不等式及其结果
2.7对数和不等式及其应用
2.8数据处理不等式
2.9充分统计量
2.10费诺不等式
相关文章:

信息论基础第二章阅读笔记
信息很难用一个简单的定义准确把握。 对于任何一个概率分布,可以定义一个熵(entropy)的量,它具有许多特性符合度量信息的直观要求。这个概念可以推广到互信息(mutual information),互信息是一种…...

Content-Type的取值
接口发送参数、接收响应数据,都需要双方约定好使用什么格式的数据,例如 json、xml。只有双方按照约定好的格式去解析数据才能正确的收发数据。而 Content-Type 就是用来告诉你数据的格式,这样我们才能知道怎么解析参数。 常见的 Content-Typ…...

【趣味JavaScript】5年前端开发都没有搞懂toString和valueOf这两个方法!
🚀 个人主页 极客小俊 ✍🏻 作者简介:web开发者、设计师、技术分享博主 🐋 希望大家多多支持一下, 我们一起进步!😄 🏅 如果文章对你有帮助的话,欢迎评论 💬点赞…...

Python中的接口是什么?
在Python中,接口是一种约定或协议,用于定义类应该实现哪些方法或属性。接口并不会提供实际的实现,而是只定义了类应该具有哪些方法和属性的签名。 Python中的接口通常通过抽象基类(Abstract Base Class,简称ABC&#…...
自学WEB后端01-安装Express+Node.js框架完成Hello World!
一、前言,网站开发扫盲知识 1.网站搭建开发包括什么? 前端 前端开发主要涉及用户界面(UI)和用户体验(UX),负责实现网站的外观和交互逻辑。前端开发使用HTML、CSS和JavaScript等技术来构建网页…...

从C语言到C++:C++入门知识(1)
朋友们、伙计们,我们又见面了,本期来给大家解读一下有关C语言的相关知识点,如果看完之后对你有一定的启发,那么请留下你的三连,祝大家心想事成! C 语 言 专 栏:C语言:从入门到精通 数…...
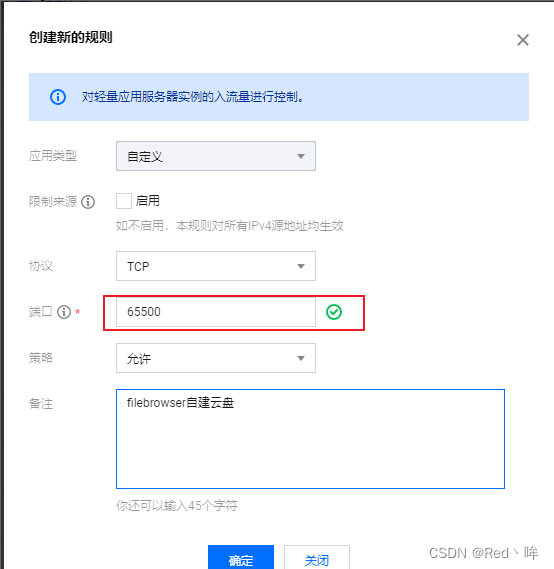
服务器(Windows系统)自建filebrowser网盘服务器超详细教程
需要依赖(工具) 轻量服务器(云服务器)一台 —— 环境Windows Server 2019filebrowser安装包(https://github.com/filebrowser/filebrowser/releases) 下载安装filebrowser 进入链接下载:https:/…...

扩展欧几里得
扩展欧几里得算法 求 a x b y d axbyd axbyd 的一组解, d gcd ( a , b ) d \gcd(a,b) dgcd(a,b)。 辗转相除递归求解。 假设已经求出 b x ( b m o d a ) y d bx (b \bmod a)y d bx(bmoda)yd 的一组解。 a x b y b x ′ ( b m o d a ) y ′ b x …...
)
MySQL 事务介绍 (事务篇 一)
什么是事务? 事务是一组操作的集合,它是一个不可分割的工作单位,事务会把所有的操作作为一个整体一起向系统提交或撤销操作请求,即这些操作要么同时成功,要么同时失败。 注意点:默认MySQL的事务是自动提交…...

nvm nodejs的版本管理工具
nvm 全英文名叫 node.js version management,是一个 nodejs 的版本管理工具,为了解决 nodejs 各种版本存在不兼容现象可以通过他安装和切换不同版本的 nodejs。 一、完全删除之前的 node 和 npm 1. 打开 cmd 命令窗口,输入 npm cache clean…...
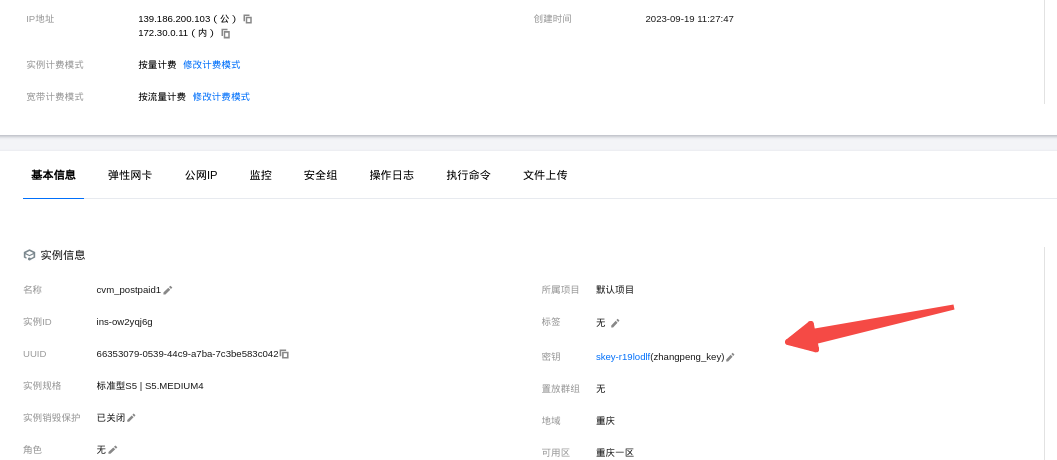
terraform简单的开始-vpc cvm创建
从网络开始 从创建VPC开始 复用前面的main.tf的代码: terraform {required_providers {tencentcloud {source "tencentcloudstack/tencentcloud"version "1.81.25"}} } variable "region" {description "腾讯云地域"…...
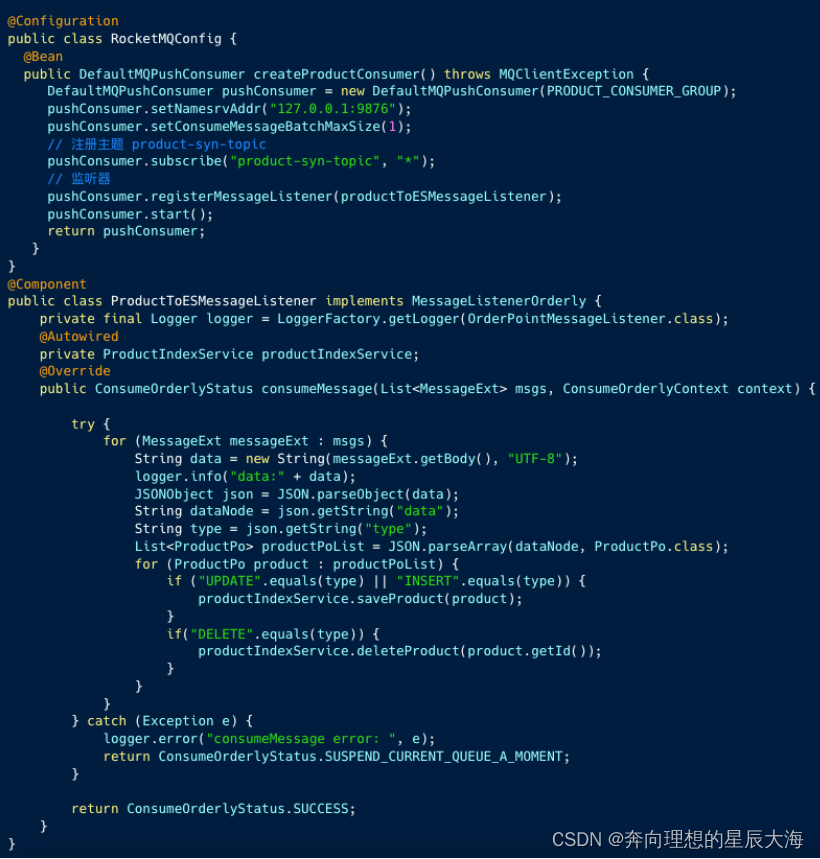
【MySQL】开启 canal同步MySQL增量数据到ES
开启 canal同步MySQL增量数据到ES canal 是阿里知名的开源项目,主要用途是基于 MySQL 数据库增量日志解析,提供增量数据订阅和消费。示使用 canal 将 MySQL 增量数据同步到ES。 一、集群模式 图中 server 对应一个 canal 运行实例 ,对应一…...
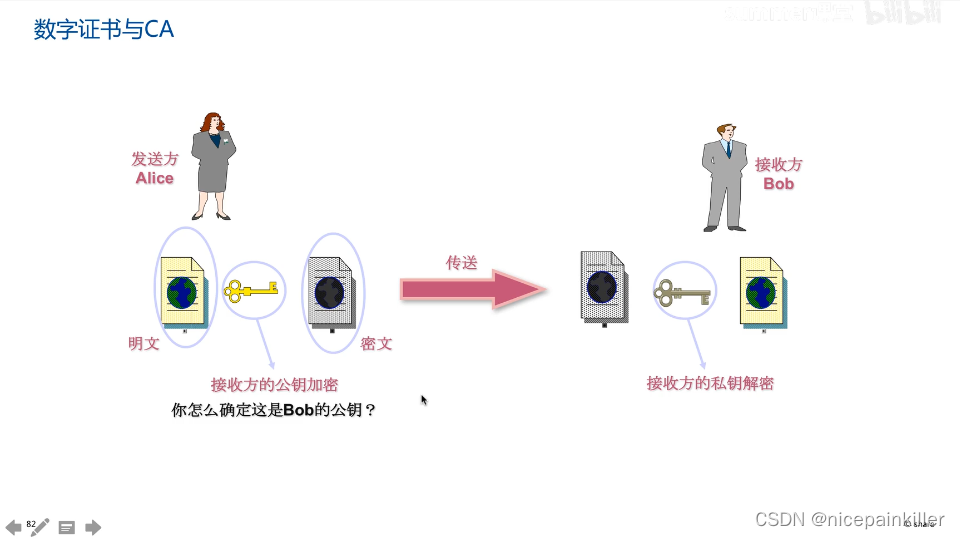
密码学概论
1.密码学的三大历史阶段: 第一阶段 古典密码学 依赖设备,主要特点 数据安全基于算法的保密,算法不公开,只要破译算法 密文就会被破解, 在1883年第一次提出 加密算法应该基于算法公开 不影响密文和秘钥的安全ÿ…...

渗透测试中的前端调试(一)
前言 前端调试是安全测试的重要组成部分。它能够帮助我们掌握网页的运行原理,包括js脚本的逻辑、加解密的方法、网络请求的参数等。利用这些信息,我们就可以更准确地发现网站的漏洞,制定出有效的攻击策略。前端知识对于安全来说,…...
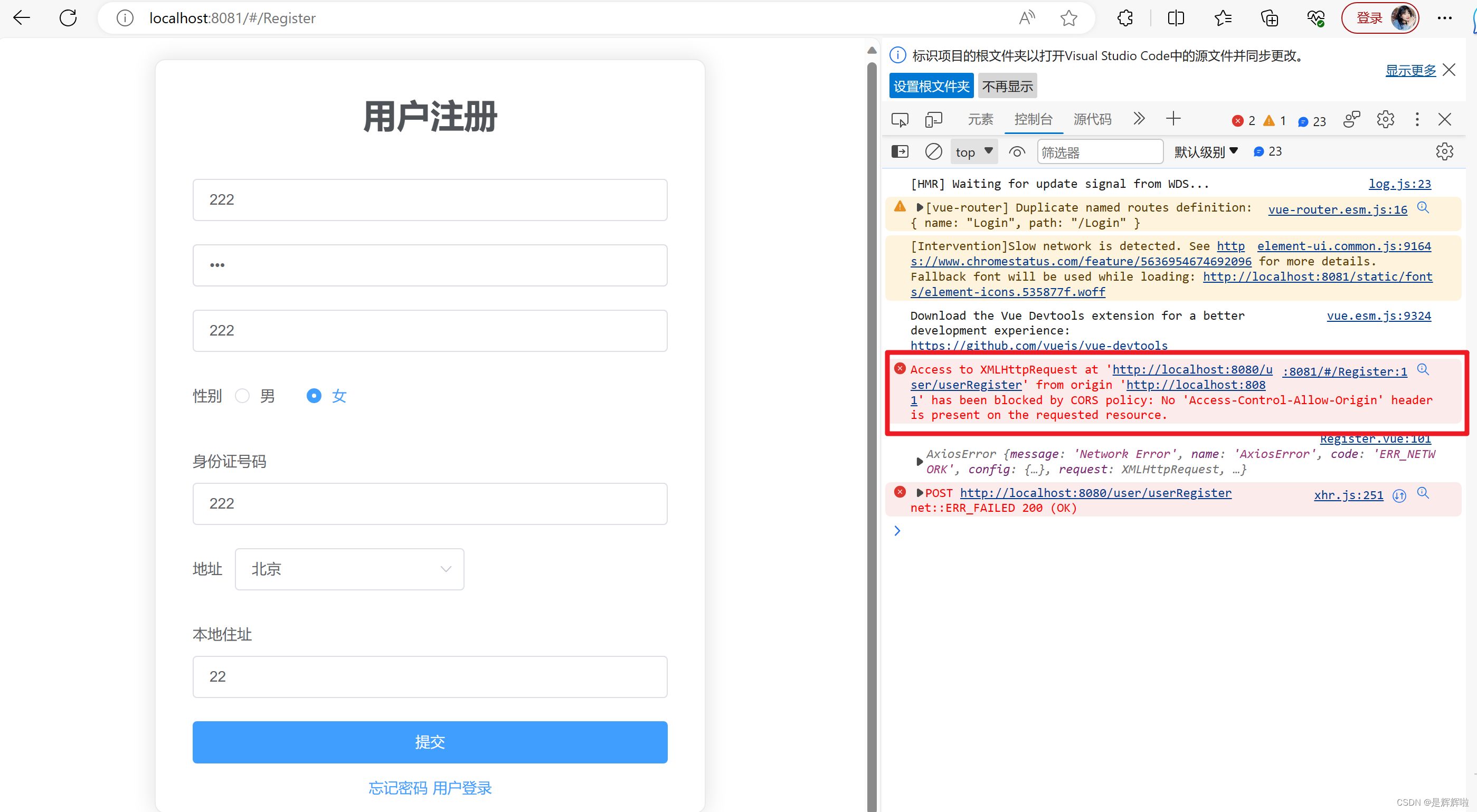
SPA项目之登录注册--请求问题(POSTGET)以及跨域问题
🥳🥳Welcome Huihuis Code World ! !🥳🥳 接下来看看由辉辉所写的关于VueElementUI的相关操作吧 目录 🥳🥳Welcome Huihuis Code World ! !🥳🥳 一.ElementUI是什么 💡…...

Spring Cloud Alibaba Gateway全局token过滤、局部过滤访问时间超过50ms日志提示
文章目录 Spring Cloud Alibaba Gateway验证token在前篇的基础上加入依赖在filter包中创建tokenFilter Spring Cloud Alibaba Gateway局部过滤1.继承AbstractGatewayFilterFactory2.仿照AddRequestHeaderGatewayFilterFactory Spring Cloud Alibaba Gateway验证token 基础搭建…...

运算符 - Go语言从入门到实战
运算符 - Go语言从入门到实战 算术运算符 假设A变量等于10,B变量等于20。 运算符描述实例相加A B 输出结果 30-相减A - B 输出结果 -10*相乘A * B 输出结果 200/相除B / A 输出结果 2%求余B % A 输出结果 0⾃增A 输出结果 11–⾃减A-- 输出结果 9 特性…...

jupyterlab开发环境最佳构建方式
文章目录 背景jupyterlab环境构建运行虚拟环境构建以及kernel映射验证总结 背景 从jupyter notebook切换到了jupyter lab. 这里记录一下本地环境的最佳构建方式. jupyter lab 安装在jupyterlab-local的anaconda 虚拟环境中.建立多个其他虚拟环境安装各种python包实现环境隔离,…...
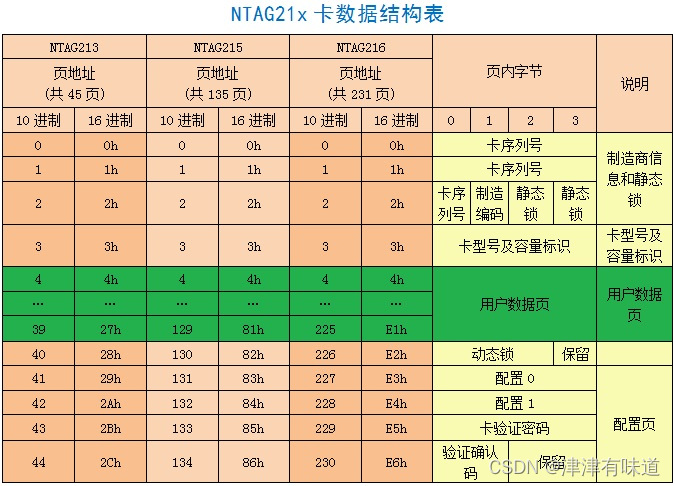
Qt_C++读写NFC标签Ntag支持windows国产linux操作系统
本示例使用的发卡器:Android Linux RFID读写器NFC发卡器WEB可编程NDEF文本/智能海报/-淘宝网 (taobao.com) ntag2标签存储结构说明 #include "mainwindow.h" #include "./ui_mainwindow.h" #include <QDebug> #include "QLibrary&…...

Web开发-基础知识扫盲
目录 Web 服务器Web 服务器例子 MVC架构Web 项目运行过程负载均衡和反向代理持久化Java对象JPA Web 服务器 Web 服务器是一种计算机程序,它通过 HTTP 协议接收和响应客户端发送的请求。Web 服务器将 HTML、CSS、JavaScript 和其他资源文件发送给客户端,…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...
