1.算法——数据结构学习
算法是解决特定问题求解步骤的描述。
从1加到100的结果
# include <stdio.h> int main(){ int i, sum = 0, n = 100; // 执行1次for(i = 1; i <= n; i++){ // 执行n + 1次sum = sum + i; // 执行n次} printf("%d", sum); // 执行1次return 0;
}
高斯求和
# include <stdio.h> int main(){ int sum = 0, n = 100; // 执行1次sum = (1 + n) * n / 2; // 执行1次printf("%d\n", sum); // 执行1次return 0;
}
概念
算法的定义
解决特定问题求解步骤的描述,在计算机中表现为指令的有限序列,并且每条指令表示一个或多个操作。
算法的特性
- 输入输出
- 具有零个或多个输入
- 至少有一个或多个输出
- 有穷性
- 执行有限步骤后会自动结束
- 每个步骤在可接受的时间内完成
- 确定性
- 每一步骤具有确定的含义
- 无二义性
- 可行性
- 每一步都必须是可行的,能在有限步内完成
算法的设计要求
- 正确性
- 算法程序没有语法错误
- 算法程序对于合法的输入数据能够产生满足要求的输出结果
- 算法程序对于非法的输入数据能够得出满足规格说明的结果
- 算法程序对于精心选择的,甚至刁难的测试数据都有满足要求的输出结果
- 可读性
- 健壮性
- 时间效率高,存储量低
算法的度量方法
事后统计法
通过设计好的测试程序和数据,利用计算机计时器对不同算法编制的程序的运行时间进行比较,从而确定算法效率的高低。
缺点:
- 必须依据算法事先编制好程序,需要花费大量时间和精力,若编制出发现是个很糟糕的算法,竹篮打水一场空
- 时间的比较以来计算机硬件和软件等环境因素,有时会掩盖算法本身的优劣
- 算法的测试数据设计困难,程序运行时间往往与数据的规模有很大关系,效率高的算法在小的测试数据面前得不到体现
事前分析估算法
在计算机程序编制前,依据统计方法对算法进行估算。
一个用高级程序语言编写的程序在计算机上运行时所消耗的时间取决于:
- 算法采用的策略和方法 —> 算法好坏的根本
- 编译产生的代码质量 —> 由软件支持
- 问题的输入规模
- 机器执行指令的速度 —> 硬件性能
一个程序的运行时间,依赖于算法的好坏和问题的输入规模(输入量)。
两种求和算法
# include <stdio.h> int main(){ int i, sum = 0, n = 100; // 执行1次for(i = 1; i <= n; i++){ // 执行n + 1次sum = sum + i; // 执行n次} printf("%d", sum); // 执行1次return 0;
}
2n+3次
# include <stdio.h> int main(){ int sum = 0, n = 100; // 执行1次sum = (1 + n) * n / 2; // 执行1次printf("%d\n", sum); // 执行1次return 0;
}
3次
延展
# include <stdio.h> int main() { int i, j, x = 0, sum = 0, n = 100; // 执行一次 for(i = 1; i <= n; i++){ for (j = 1; j <= n; j++){ x++; // 执行n×n次 sum = sum + x; } } printf("%d", sum); // 执行一次 return 0;
}
测定运行时间最可靠的方法就是计算对运行时间有消耗的的基本操作的执行次数。
-
不计循环索引的递增、循环终止条件、变量声明、打印结果等操作
-
分析程序的运行时间时,最重要的是把程序看成是独立于程序设计语言的算法或一系列步骤
-
分析一个算法的运行时间,重要的是把基本操作的数量和输入规模关联起来,即基本操作的数量必须表示成输入规模的函数
函数的渐近增长
给定两个函数f(n)和g(n),若存在一个整数N,使得对于所有n>N,f(n)总是比g(n)大,那么我们说f(n)的增长渐近快于g(n)
- 可以忽略加减常数
- 与最高次项相乘的常数并不重要
判断一个算法的效率时,函数中的常数和其他次要项常常可忽略,而更应该关注最高阶项的阶数。
某个算法,随着n的增大,它会越来越优于另一算法或越来越差于另一算法。
算法的时间复杂度
进行算法分析时,语句总的执行次数T(n)是关于问题规模n的函数,进而分析T(n)随n的变化情况并确定T(n)的数量级。
- 算法的时间复杂度,也就是算法的时间度量,记作T(n)=O(f(n)) —> 大O记法
- 它随问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐进时间复杂度,简称:时间复杂度
- f(n)是问题规模n的某个函数
增长最慢的算法为最优算法。
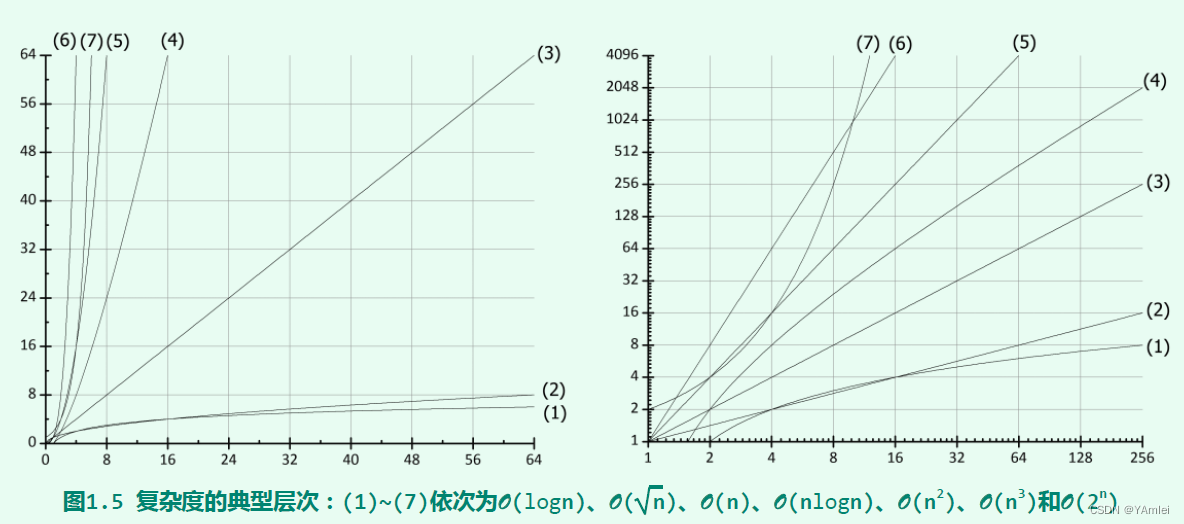
推导大O阶方法
- 用常数1取代运行时间中的所有加法常数
- 在修改后的运行次数中函数中,只保留最高阶项
- 如果最高阶项存在且系数不是1,则去除与这个项相乘的系数
常数阶 O(1)
顺序结构的时间复杂度。
执行时间恒定的算法:O(1)的时间复杂度 —> 常数阶
不论常数为多少,都记作O(1)!
对于分支结构而言,无论真假,执行的次数都是恒定的,不会随着n的变大而发生变化,单纯的分支结构 -> 复杂度也为O(1)
线性阶 O(n)
线性阶的循环结构。
要确定某个算法的阶数,常需要确定某个特定语句或某个语句集的运行次数。
分析算法的复杂度,关键就是要分析循环结构的运行情况!
int i;
for(i = 0; i < n; i++){ // 时间复杂度为O(1)的程序步骤序列
}
对数阶 O(logn)
int count = 1;
while (count < n){ count = count * 2; // 时间复杂度为O(1)的程序步骤序列
}
每次count乘2后,离n就近一分, 2 x = n , x = log 2 n 2^x=n,x=\log_{2}n 2x=n,x=log2n
平方阶 O( n 2 n^2 n2)
int i,j;
for(i = 0; i < n; i++){ for(j = 0; j < n; j++){ // 时间复杂度为O(1)的程序步骤序列 }
}
循环的时间复杂度等于循环体的复杂度乘以该循环的次数。
理解大O阶推导不算难,难的是对数列的一些相关运算,更多的是考察数学知识和能力!特别是数列方面的知识和解题能力!
常见时间复杂度表

最坏与平均情况
最坏情况是一种保证,通常我们提到的运行时间都是最坏情况的运行时间。
平均运行时间是所有情况中最有意义的,因为它是期望的运行时间。
算法空间复杂度
计算公式:S(n)=O(f(n))
n -> 问题的规模,f(n)为语句关于n所占存储空间的函数
一般情况,一个程序在机器上执行时,除了需要存储程序本身的指令、常数、变量和输入数据外,还需要存储对数据操作的存储单元。
通常使用“时间复杂度”指运行时间的需求;使用“空间复杂度”指空间需求。
不用限定词地使用“复杂度”时,通常指:时间复杂度
相关文章:

1.算法——数据结构学习
算法是解决特定问题求解步骤的描述。 从1加到100的结果 # include <stdio.h> int main(){ int i, sum 0, n 100; // 执行1次for(i 1; i < n; i){ // 执行n 1次sum sum i; // 执行n次} printf("%d", sum); // 执行1次return 0; }高斯求和…...

信息论基础第二章阅读笔记
信息很难用一个简单的定义准确把握。 对于任何一个概率分布,可以定义一个熵(entropy)的量,它具有许多特性符合度量信息的直观要求。这个概念可以推广到互信息(mutual information),互信息是一种…...

Content-Type的取值
接口发送参数、接收响应数据,都需要双方约定好使用什么格式的数据,例如 json、xml。只有双方按照约定好的格式去解析数据才能正确的收发数据。而 Content-Type 就是用来告诉你数据的格式,这样我们才能知道怎么解析参数。 常见的 Content-Typ…...

【趣味JavaScript】5年前端开发都没有搞懂toString和valueOf这两个方法!
🚀 个人主页 极客小俊 ✍🏻 作者简介:web开发者、设计师、技术分享博主 🐋 希望大家多多支持一下, 我们一起进步!😄 🏅 如果文章对你有帮助的话,欢迎评论 💬点赞…...

Python中的接口是什么?
在Python中,接口是一种约定或协议,用于定义类应该实现哪些方法或属性。接口并不会提供实际的实现,而是只定义了类应该具有哪些方法和属性的签名。 Python中的接口通常通过抽象基类(Abstract Base Class,简称ABC&#…...
自学WEB后端01-安装Express+Node.js框架完成Hello World!
一、前言,网站开发扫盲知识 1.网站搭建开发包括什么? 前端 前端开发主要涉及用户界面(UI)和用户体验(UX),负责实现网站的外观和交互逻辑。前端开发使用HTML、CSS和JavaScript等技术来构建网页…...

从C语言到C++:C++入门知识(1)
朋友们、伙计们,我们又见面了,本期来给大家解读一下有关C语言的相关知识点,如果看完之后对你有一定的启发,那么请留下你的三连,祝大家心想事成! C 语 言 专 栏:C语言:从入门到精通 数…...
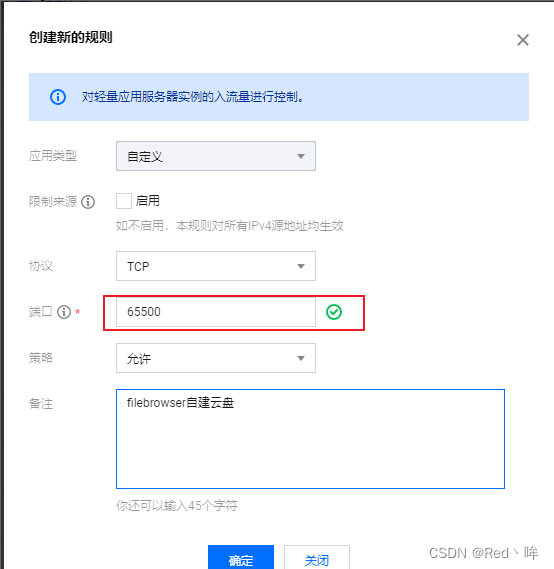
服务器(Windows系统)自建filebrowser网盘服务器超详细教程
需要依赖(工具) 轻量服务器(云服务器)一台 —— 环境Windows Server 2019filebrowser安装包(https://github.com/filebrowser/filebrowser/releases) 下载安装filebrowser 进入链接下载:https:/…...

扩展欧几里得
扩展欧几里得算法 求 a x b y d axbyd axbyd 的一组解, d gcd ( a , b ) d \gcd(a,b) dgcd(a,b)。 辗转相除递归求解。 假设已经求出 b x ( b m o d a ) y d bx (b \bmod a)y d bx(bmoda)yd 的一组解。 a x b y b x ′ ( b m o d a ) y ′ b x …...
)
MySQL 事务介绍 (事务篇 一)
什么是事务? 事务是一组操作的集合,它是一个不可分割的工作单位,事务会把所有的操作作为一个整体一起向系统提交或撤销操作请求,即这些操作要么同时成功,要么同时失败。 注意点:默认MySQL的事务是自动提交…...

nvm nodejs的版本管理工具
nvm 全英文名叫 node.js version management,是一个 nodejs 的版本管理工具,为了解决 nodejs 各种版本存在不兼容现象可以通过他安装和切换不同版本的 nodejs。 一、完全删除之前的 node 和 npm 1. 打开 cmd 命令窗口,输入 npm cache clean…...
terraform简单的开始-vpc cvm创建
从网络开始 从创建VPC开始 复用前面的main.tf的代码: terraform {required_providers {tencentcloud {source "tencentcloudstack/tencentcloud"version "1.81.25"}} } variable "region" {description "腾讯云地域"…...
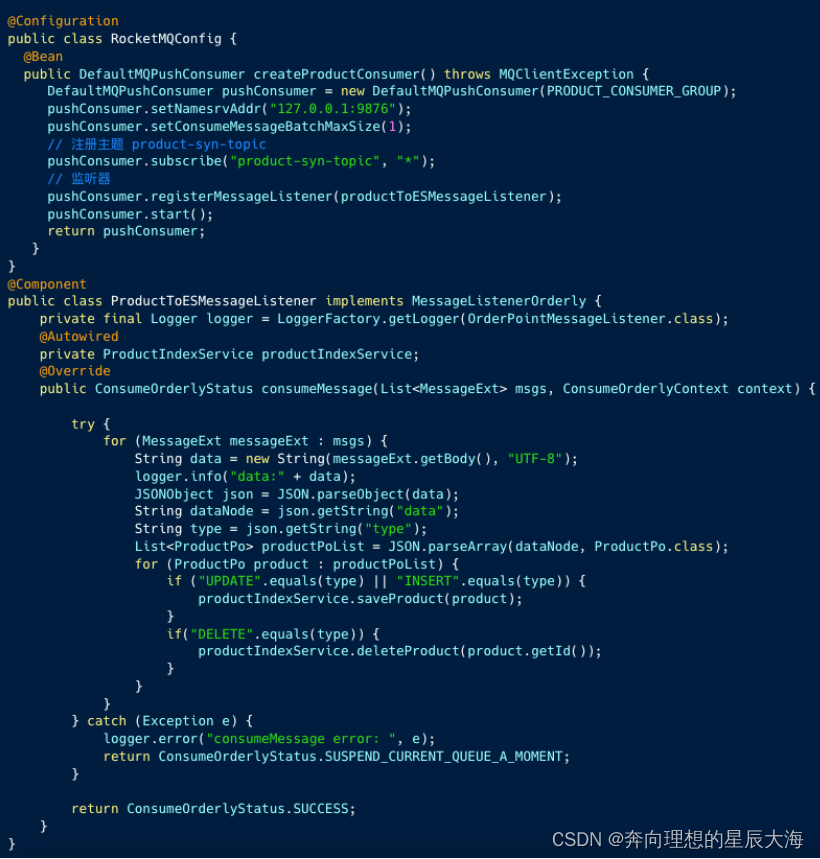
【MySQL】开启 canal同步MySQL增量数据到ES
开启 canal同步MySQL增量数据到ES canal 是阿里知名的开源项目,主要用途是基于 MySQL 数据库增量日志解析,提供增量数据订阅和消费。示使用 canal 将 MySQL 增量数据同步到ES。 一、集群模式 图中 server 对应一个 canal 运行实例 ,对应一…...
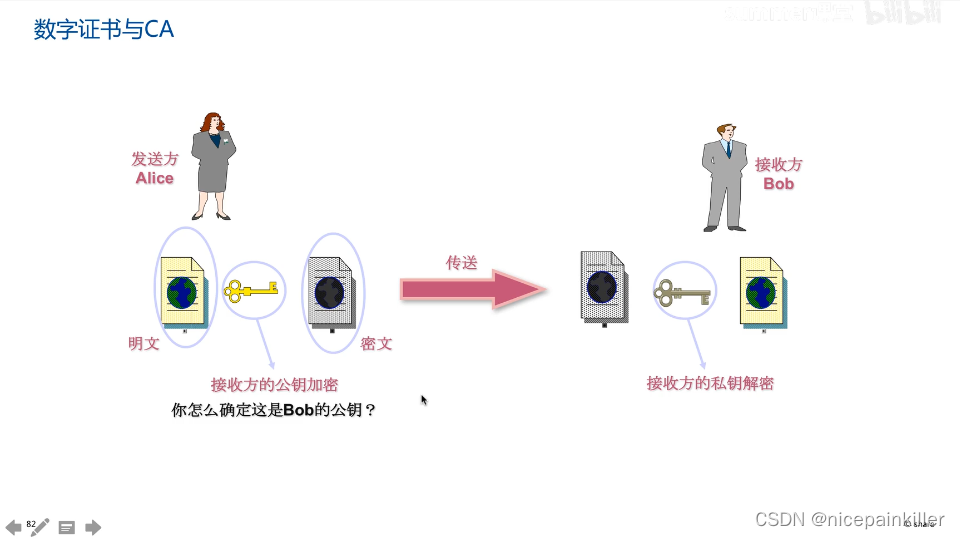
密码学概论
1.密码学的三大历史阶段: 第一阶段 古典密码学 依赖设备,主要特点 数据安全基于算法的保密,算法不公开,只要破译算法 密文就会被破解, 在1883年第一次提出 加密算法应该基于算法公开 不影响密文和秘钥的安全ÿ…...

渗透测试中的前端调试(一)
前言 前端调试是安全测试的重要组成部分。它能够帮助我们掌握网页的运行原理,包括js脚本的逻辑、加解密的方法、网络请求的参数等。利用这些信息,我们就可以更准确地发现网站的漏洞,制定出有效的攻击策略。前端知识对于安全来说,…...
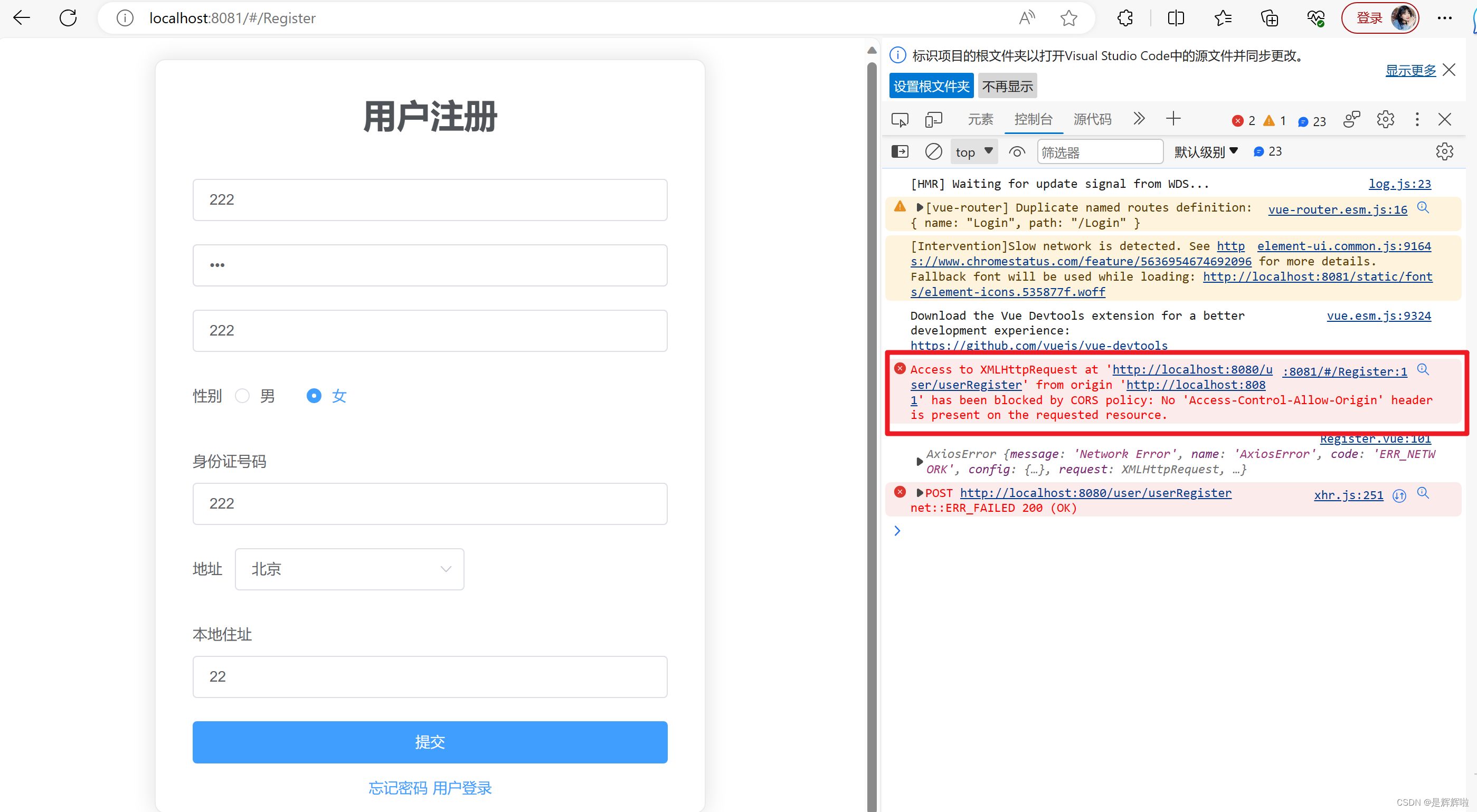
SPA项目之登录注册--请求问题(POSTGET)以及跨域问题
🥳🥳Welcome Huihuis Code World ! !🥳🥳 接下来看看由辉辉所写的关于VueElementUI的相关操作吧 目录 🥳🥳Welcome Huihuis Code World ! !🥳🥳 一.ElementUI是什么 💡…...

Spring Cloud Alibaba Gateway全局token过滤、局部过滤访问时间超过50ms日志提示
文章目录 Spring Cloud Alibaba Gateway验证token在前篇的基础上加入依赖在filter包中创建tokenFilter Spring Cloud Alibaba Gateway局部过滤1.继承AbstractGatewayFilterFactory2.仿照AddRequestHeaderGatewayFilterFactory Spring Cloud Alibaba Gateway验证token 基础搭建…...

运算符 - Go语言从入门到实战
运算符 - Go语言从入门到实战 算术运算符 假设A变量等于10,B变量等于20。 运算符描述实例相加A B 输出结果 30-相减A - B 输出结果 -10*相乘A * B 输出结果 200/相除B / A 输出结果 2%求余B % A 输出结果 0⾃增A 输出结果 11–⾃减A-- 输出结果 9 特性…...

jupyterlab开发环境最佳构建方式
文章目录 背景jupyterlab环境构建运行虚拟环境构建以及kernel映射验证总结 背景 从jupyter notebook切换到了jupyter lab. 这里记录一下本地环境的最佳构建方式. jupyter lab 安装在jupyterlab-local的anaconda 虚拟环境中.建立多个其他虚拟环境安装各种python包实现环境隔离,…...
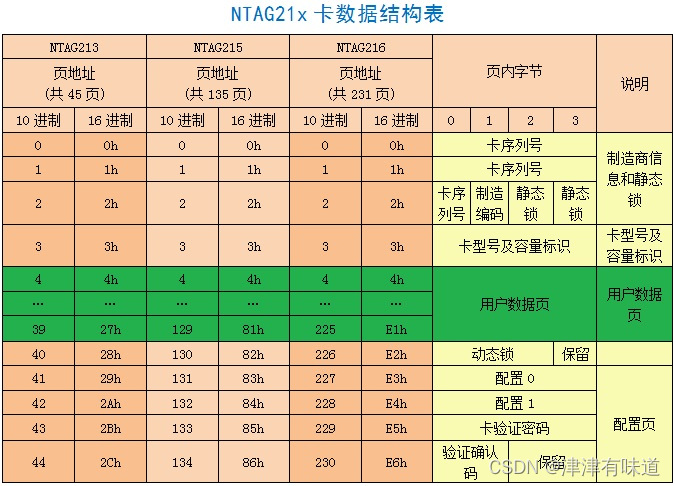
Qt_C++读写NFC标签Ntag支持windows国产linux操作系统
本示例使用的发卡器:Android Linux RFID读写器NFC发卡器WEB可编程NDEF文本/智能海报/-淘宝网 (taobao.com) ntag2标签存储结构说明 #include "mainwindow.h" #include "./ui_mainwindow.h" #include <QDebug> #include "QLibrary&…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...
