当前位置： 首页 > news >正文

maven中relativepath标签的含义

news 2026/2/10 1:45:30

一  relative标签的含义

1.1 作用

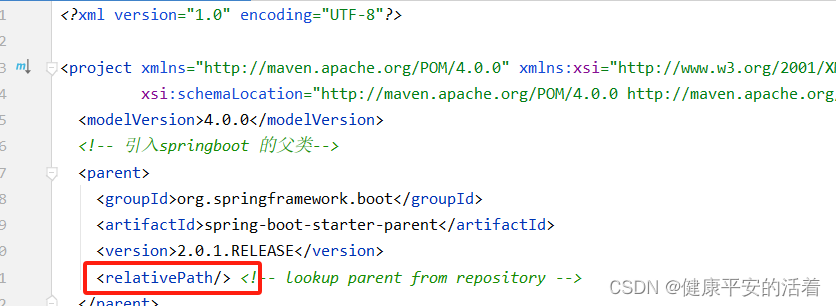
这个<parent>下面的<relativePath>属性：parent的pom文件的路径。

relativePath 的作用是为了找到父级工程的pom.xml;因为子工程需要继承父工程的pom.xml文件中的内容。然后relativePath 标签内的值使用相对路径定位到父工程的pom.xml。

父项目的pom.xml文件的相对路径。相对路径允许你选择一个不同的路径。默认值是../pom.xml。Maven首先在构建当前项目的地方寻找父项 目的pom，其次在文件系统的这个位置（relativePath位置），然后在本地仓库，最后在远程仓库寻找父项目的pom。

1.默认我们不用写<relativePath>，那默认值就是../pom.xml，会从上级目录中获取parent的pom，我们建多模块的项目就是这个情况。 

2.<relativePath/>： 设定一个空值将始终从仓库中获取，不从本地路径获取。很常见的场景就是使用springboot的时候

3.<relativePath>xxxxxx<relativePath/>  这种也很显然，指定一个xxxx本地的路径，从xxxx本地路径获取parent的 pom。

1.2 查找顺序

1.没有relativePath标签等同<relativePath>../pom.xml</relativePath>, 即默认从当前pom文件的上一级目录找。

2.<relativePath/>表示不从relativePath找, 直接从本地仓库找,找不到再从远程仓库找

MAVEN构建jar包时候查找顺序：relativePath元素中的地址>本地仓库>远程仓库

相关文章：

maven中relativepath标签的含义

一 relative标签的含义 1.1 作用 这个<parent>下面的<relativePath>属性&#xff1a;parent的pom文件的路径。 relativePath 的作用是为了找到父级工程的pom.xml;因为子工程需要继承父工程的pom.xml文件中的内容。然后relativePath 标签内的值使用相对路径定位…...

编程日记 2023/9/27 13:01:00

Greenplum 对比 Hadoop

Greenplum属于MPP架构&#xff0c;和Hadoop一样都是为了解决大规模数据的并行计算而出现的技术&#xff0c;两者的相似点在于&#xff1a; 分布式存储&#xff0c;数据分布在多个节点服务器上分布式并行计算框架支持横向扩展来提高整体的计算能力和存储容量都支持X86开放集群架…...

编程日记 2023/9/27 12:59:59

OJ练习第182题——字典树（前缀树）

字典树&#xff08;前缀树&#xff09; 208. 实现 Trie (前缀树)题目描述示例知识补充官解代码 211. 添加与搜索单词 - 数据结构设计题目描述示例思路Java代码 208. 实现 Trie (前缀树) 力扣链接&#xff1a;208. 实现 Trie (前缀树) 题目描述 示例 知识补充 插入字符串 我…...

编程日记 2023/9/27 12:58:58

前端知识总结

在前端开发中&#xff0c;y x是一种常见的自增运算符的使用方式。它表示将变量x的值自增1&#xff0c;并将自增后的值赋给变量y。 具体来说&#xff0c;x是一种后缀自增运算符&#xff0c;表示将变量x的值自增1。而y x则是将自增前的值赋给变量y。这意味着在执行y x之后&am…...

编程日记 2023/9/27 12:57:57

中国JP-10燃料行业市场研究与预测报告（2023版）

内容简介&#xff1a; 高密度燃料是指以石油基、煤基和生物质基烃类为原料&#xff0c;通过聚合、加氢、异构等工艺合成的密度大于0.85 gcm-3的饱和多环碳氢化合物&#xff0c;广泛应用于航空航天领域。由于高密度燃料密度大和体积热值高等特点&#xff0c;飞行器在油箱体积一…...

编程日记 2023/9/27 12:55:56

护眼灯显色指数应达多少？眼科医生推荐灯光显色指数多少合适

台灯的显色指数是其非常重要的指标&#xff0c;它可以表示灯光照射到物体身上&#xff0c;物体颜色的真实程度&#xff0c;一般用平均显色指数Ra来表示&#xff0c;Ra值越高&#xff0c;灯光显色能力越强。常见的台灯显色指数最低要求一般是在Ra80以上即可&#xff0c;比较好的…...

编程日记 2023/9/27 12:54:55

AI 大模型

随着人工智能技术的迅猛发展&#xff0c;AI 大模型逐渐成为推动人工智能领域提升的关键因素&#xff0c;大模型已成为了引领技术浪潮研究和应用方向。大模型即大规模预训练模型&#xff0c;通常是指那些在大规模数据上进行了预训练的具有庞大规模和复杂结构的人工智能模型&…...

编程日记 2023/9/27 12:53:54

一个案例熟悉使用pytorch

文章目录 1. 完整模型的训练套路1.2 导入必要的包1.3 准备数据集1.3.1 使用公开数据集&#xff1a;1.3.2 获取训练集、测试集长度&#xff1a;1.3.3 利用 DataLoader来加载数据集 1.4 搭建神经网络1.4.1 测试搭建的模型1.4.2 创建用于训练的模型 1.5 定义损失函数和优化器1.6 使…...

编程日记 2023/9/27 12:51:52

MySQL - limit 分页查询 （查询操作 五）

功能介绍&#xff1a;分页查询&#xff08;limit&#xff09;是一种常用的数据库查询技术&#xff0c;它允许我们从数据库表中按照指定的数量和顺序获取数据&#xff0c;它在处理大量数据时特别有用&#xff0c;可以提高查询效率并减少网络传输的数据 语法&#xff1a;SELECT …...

编程日记 2023/9/27 12:50:51

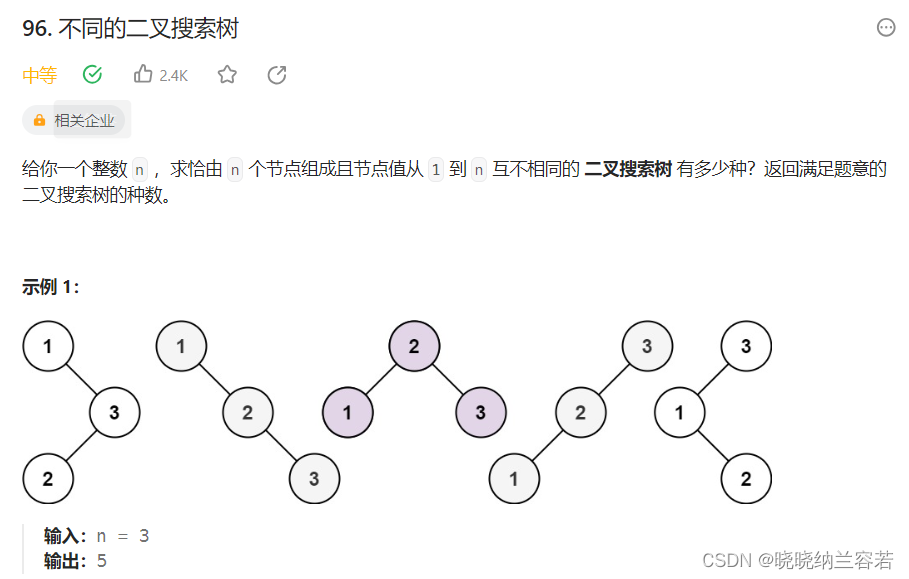
代码随想录笔记--动态规划篇

1--动态规划理论基础 动态规划经典问题&#xff1a;① 背包问题&#xff1b;② 打家劫舍&#xff1b;③ 股票问题&#xff1b; ④ 子序列问题&#xff1b; 动态规划五部曲&#xff1a; ① 确定 dp 数组及其下标的含义&#xff1b; ② 确定递推公式&#xff1b; ③ 确定 dp 数组…...

编程日记 2023/9/27 12:48:50

vue之vuex

Vuex 是 Vue.js 的一个状态管理模式和库&#xff0c;为应用中的所有组件提供了一个集中式的存储管理&#xff0c;并提供了一种强大的方式来管理应用的状态。Vuex 包含以下核心概念&#xff1a; State&#xff1a;定义了应用的状态&#xff0c;类似于组件中的 data。 Getters&a…...

编程日记 2023/9/27 12:47:48

ISO 26262 系列学习笔记 ———— ASIL定义（Automotive Safety Integration Level）

文章目录 介绍严重度&#xff08;Severity&#xff09;暴露概率&#xff08;Probability of Exposure&#xff09;可控性&#xff08;Controllability&#xff09; 介绍 如果没有另行说明&#xff0c;则应满足ASIL A、B、C和D各分条款的要求或建议。这些要求和建议参考了安全目…...

编程日记 2023/9/27 12:46:47

代码随想录 第8章 二叉树

1、理论知识 &#xff08;1&#xff09;、满二叉树 如果一棵二叉树只有度为0的节点和度为2的节点&#xff0c;并且度为0的节点在同一层上&#xff0c;则这棵二叉树为满二叉树。 &#xff08;2&#xff09;、完全二叉树 除了底层节点可能没有填满&#xff0c;其余每层的节点…...

编程日记 2023/9/27 12:45:46

计算机网络工程师多选题系列——计算机网络

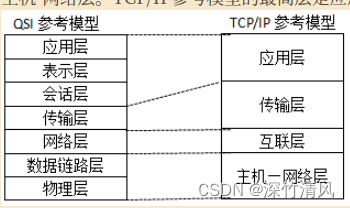
2 计算机网络 2.1 网络技术基础 题型1 TCP/IP与ISO模型的问题 TCP/IP由IETF制定&#xff0c;ISO由OSI制定&#xff1b; TCP/IP分为四层&#xff0c;分别是主机-网络层、互联网络层、传输层和应用层&#xff1b;OSI分为七层&#xff0c;分别是物理层、数据链路层、网络层(实…...

编程日记 2023/9/27 12:43:45

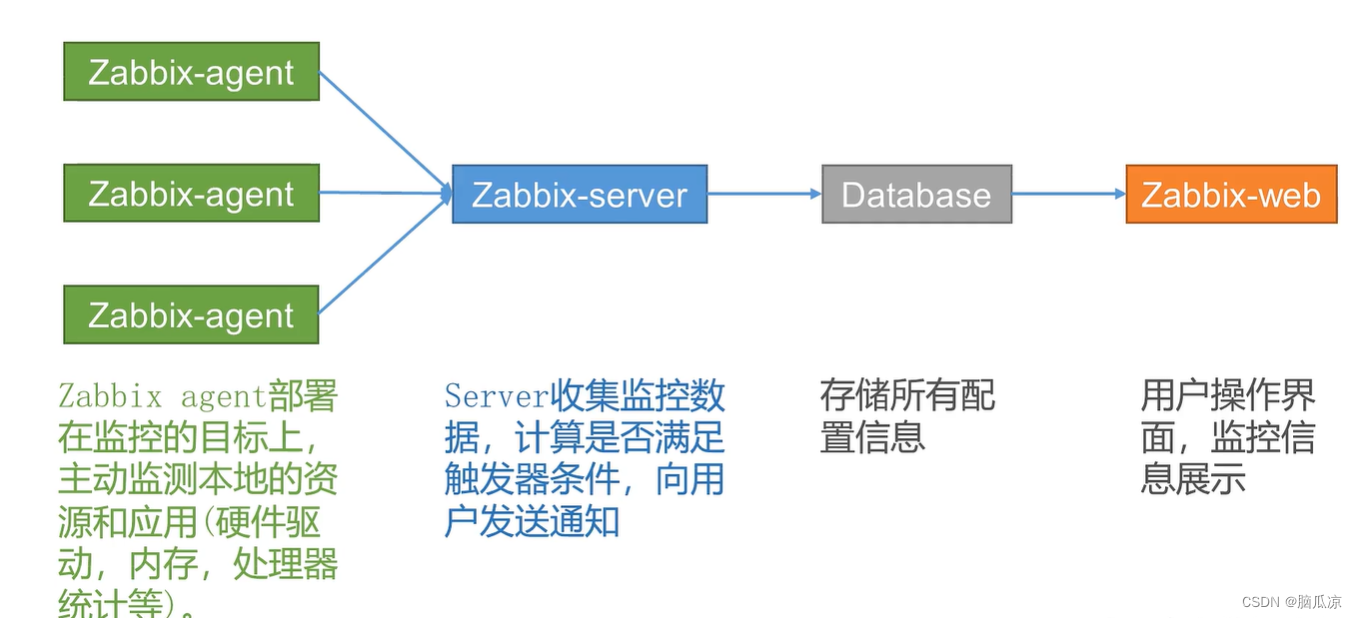
Zabbix5.0_介绍_组成架构_以及和prometheus的对比_大数据环境下的监控_网络_软件_设备监控_Zabbix工作笔记001

z 这里Zabbix可以实现采集 存储 展示 报警 但是 zabbix自带的,展示 和报警 没那么好看,我们可以用 grafana进行展示,然后我们用一个叫睿象云的来做告警展示, 会更丰富一点. 可以看到 看一下zabbix的介绍. 对zabbix的介绍,这个zabbix比较适合对服务器进行监控 这个是zabbix的…...

编程日记 2023/9/27 12:42:44

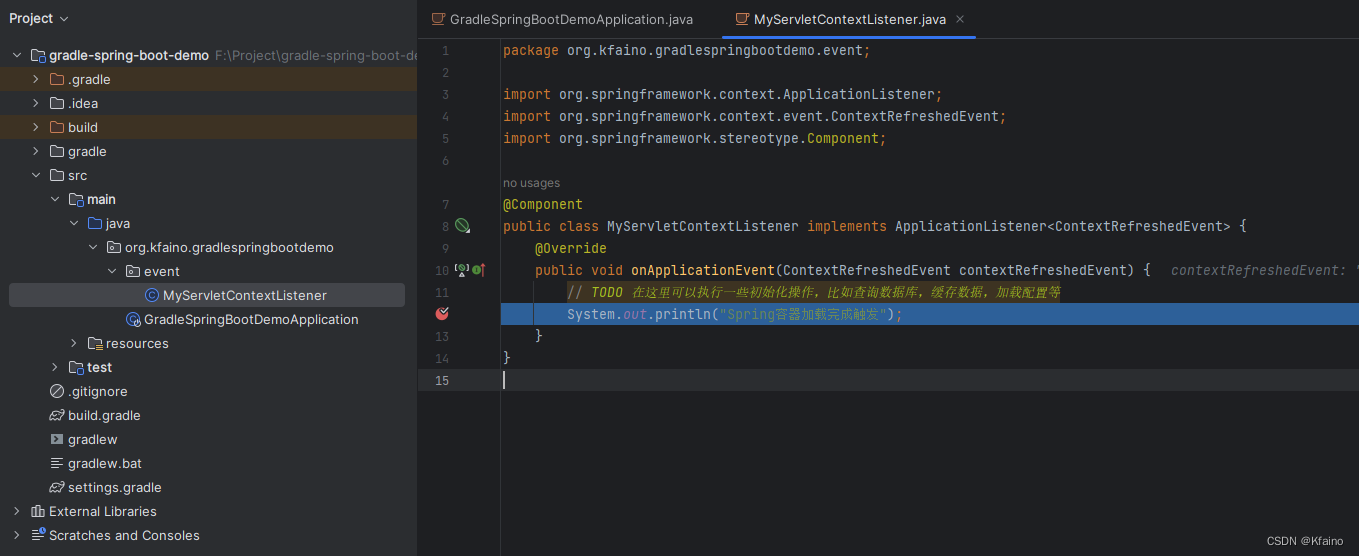
Spring | 事件监听器应用与最佳实践

引言 在复杂的软件开发环境中&#xff0c;组件之间的通信和信息交流显得尤为重要。Spring框架&#xff0c;作为Java世界中最受欢迎的开发框架之一&#xff0c;提供了一种强大的事件监听器模型&#xff0c;使得组件间的通信变得更加灵活和解耦。本文主要探讨Spring事件监听器的…...

编程日记 2023/9/27 12:40:42

正点原子lwIP学习笔记——NETCONN接口简介

1. NETCONN接口简介 NETCONN API 使用了操作系统的 IPC 机制&#xff0c; 对网络连接进行了抽象&#xff0c;使用同一的接口完成UDP和TCP连接。 NETCONN API接口是在RAW接口基础上延申出来的一套API接口 首先会调用netconn_new创建一个pcb控制块&#xff0c;其实际是一个宏定…...

编程日记 2023/9/27 12:39:41

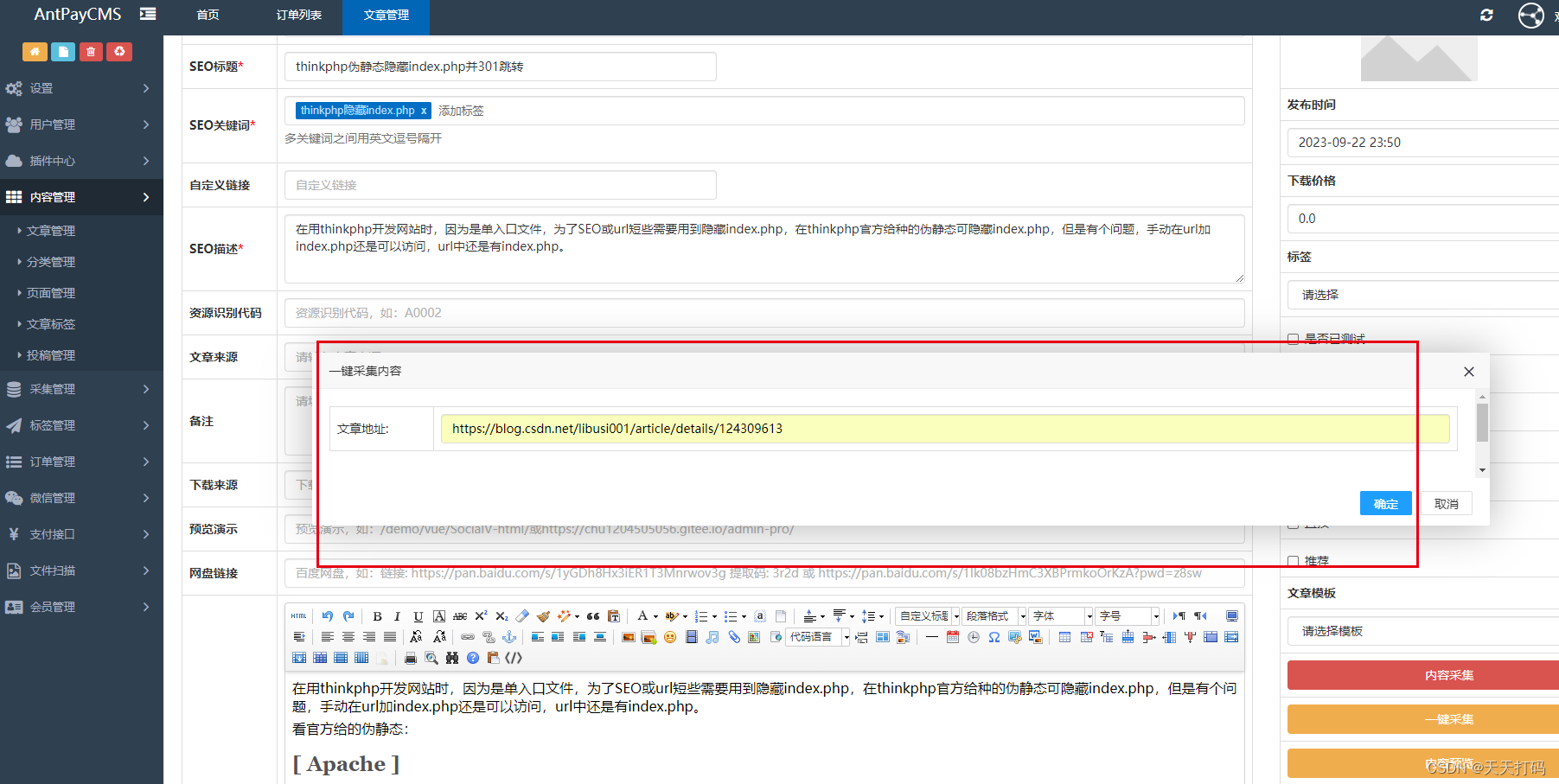
PHP自动识别采集何意网址文章正文内容

在做PHP采集内容时&#xff0c;用过querylist采集组件&#xff0c;但是这个插件采集页面内容时&#xff0c;都必须要写个采集选择器。这样比较麻烦&#xff0c;每个文章页面都必须指定一条采集规则 。就开始着手找一个插件可以能自动识别任意文章url正文内容并采集的&#xff0…...

编程日记 2023/9/27 12:36:39

区块链实验室(27) - 区块链+物联网应用案例

分享最新的区块链物联网应用案例&#xff1a;HPCLS-BC...

编程日记 2023/9/27 12:35:38

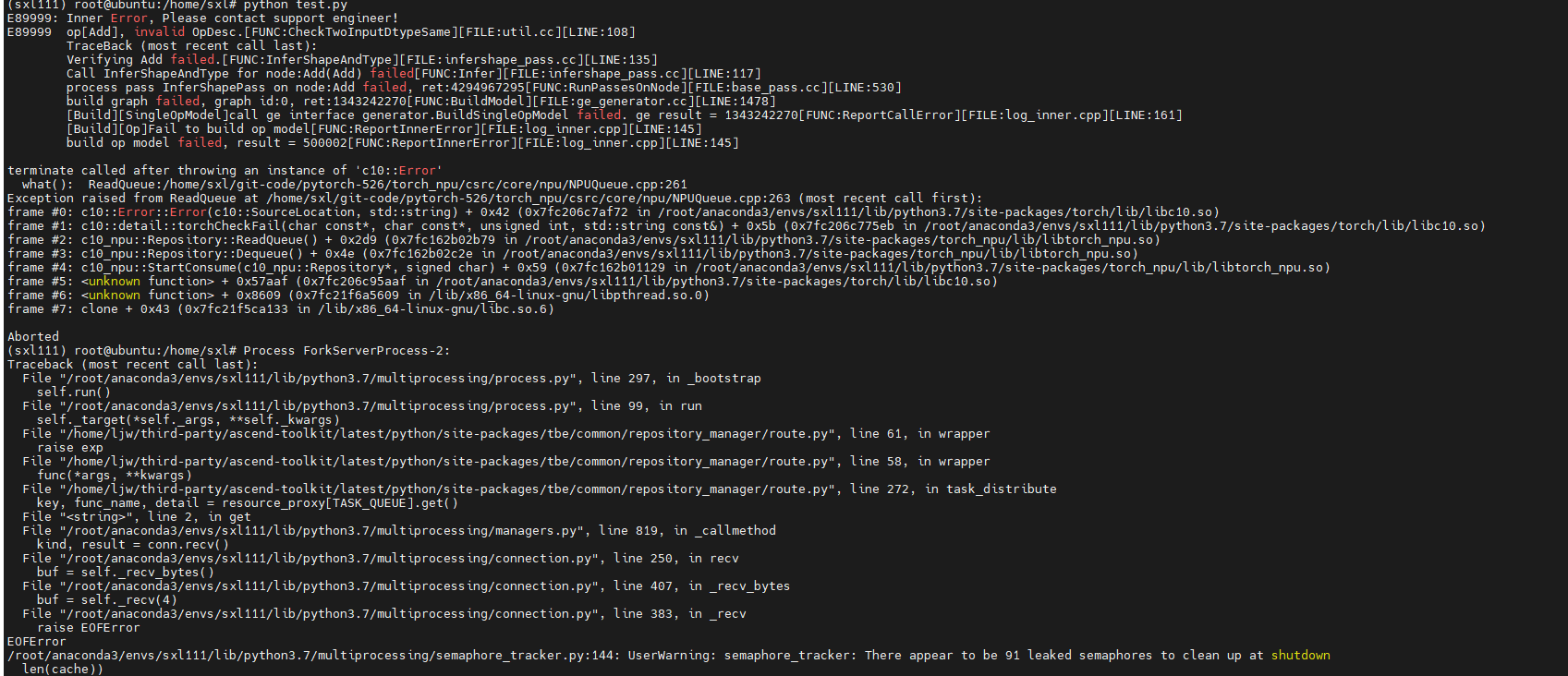
NPU上PyTorch模型训练问题案例

在昇腾AI处理器上训练PyTorch框架模型时&#xff0c;可能由于环境变量设置问题、训练脚本代码问题&#xff0c;导致打印出的堆栈报错与实际错误并不一致、脚本运行异常等问题&#xff0c;那么本期就分享几个关于PyTorch模型训练问题的典型案例&#xff0c;并给出原因分析及解决…...

编程日记 2023/9/27 12:34:37

Map相关知识

数据结构 二叉树 二叉树&#xff0c;顾名思义&#xff0c;每个节点最多有两个“叉”&#xff0c;也就是两个子节点&#xff0c;分别是左子 节点和右子节点。不过&#xff0c;二叉树并不要求每个节点都有两个子节点&#xff0c;有的节点只 有左子节点&#xff0c;有的节点只有…...

编程新知 2026/2/4 16:21:14

CSS设置元素的宽度根据其内容自动调整

width: fit-content 是 CSS 中的一个属性值&#xff0c;用于设置元素的宽度根据其内容自动调整&#xff0c;确保宽度刚好容纳内容而不会超出。 效果对比 默认情况&#xff08;width: auto&#xff09;&#xff1a; 块级元素&#xff08;如 <div>&#xff09;会占满父容器…...

编程新知 2025/10/16 16:03:09

#Uniapp篇：chrome调试unapp适配

chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器&#xff1a;Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

编程新知 2026/1/4 21:36:42

区块链技术概述

区块链技术是一种去中心化、分布式账本技术&#xff0c;通过密码学、共识机制和智能合约等核心组件&#xff0c;实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点&#xff1a;数据存储在网络中的多个节点&#xff08;计算机&#xff09;&#xff0c;而非…...

编程新知 2025/10/25 7:41:33

LangChain 中的文档加载器（Loader）与文本切分器（Splitter）详解《二》

&#x1f9e0; LangChain 中 TextSplitter 的使用详解&#xff1a;从基础到进阶&#xff08;附代码&#xff09; 一、前言 在处理大规模文本数据时&#xff0c;特别是在构建知识库或进行大模型训练与推理时&#xff0c;文本切分&#xff08;Text Splitting&#xff09; 是一个…...

编程新知 2025/10/10 9:24:44

yaml读取写入常见错误 (‘cannot represent an object‘, 117)

错误一&#xff1a;yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因&#xff0c;后面把yaml.safe_dump直接替换成yaml.dump&#xff0c;确实能保存&#xff0c;但出现乱码&#xff1a; 放弃yaml.dump&#xff0c;又切…...

编程新知 2026/2/4 11:44:10

Spring AOP代理对象生成原理

代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】&#xff0c;这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...

编程新知 2026/2/6 22:31:04

命令行关闭Windows防火墙

命令行关闭Windows防火墙 引言一、防火墙：被低估的"智能安检员"二、优先尝试！90%问题无需关闭防火墙方案1：程序白名单（解决软件误拦截）方案2：开放特定端口（解决网游/开发端口不通）三、命令行极速关闭方案方法一：PowerShell（推荐Win10/11）​方法二：CMD命令…...

编程新知 2025/8/27 20:07:03

写一个shell脚本，把局域网内，把能ping通的IP和不能ping通的IP分类，并保存到两个文本文件里

写一个shell脚本&#xff0c;把局域网内&#xff0c;把能ping通的IP和不能ping通的IP分类&#xff0c;并保存到两个文本文件里 脚本1 #!/bin/bash #定义变量 ip10.1.1 #循环去ping主机的IP for ((i1;i<10;i)) doping -c1 $ip.$i &>/dev/null[ $? -eq 0 ] &&am…...

编程新知 2025/11/23 13:02:26

算法250609 高精度

加法 #include<stdio.h> #include<iostream> #include<string.h> #include<math.h> #include<algorithm> using namespace std; char input1[205]; char input2[205]; int main(){while(scanf("%s%s",input1,input2)!EOF){int a[205]…...

编程新知 2025/9/17 10:04:40