数据结构与算法基础-(3)
🌈write in front🌈
🧸大家好,我是Aileen🧸.希望你看完之后,能对你有所帮助,不足请指正!共同学习交流.
🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如需转载还请通知⚠️
📝个人主页:Aileen_0v0🧸—CSDN博客
🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝
📣系列专栏:Aileen_0v0🧸的数据结构与算法学习系列专栏🌸——CSDN博客
🗼我的格言:"没有罗马,那就自己创造罗马💫~"


目录
回顾💫
List 列表数据类型常用操作性能
Dict字典数据类型常用操作性能
P、NP、NPC、NP-hard问题详解
1. 多项式时间(Polynomial time)
2. 确定性算法与非确定性算法
确定性算法:
非确定性算法:
3. 规约/约化
4. P类问题、NP类问题、NPC问题
P类问题:
NP类问题:
NPC问题(NP-complete):
NP难问题:

回顾💫
"温故而知新"~
上回儿说到,什么是时间复杂度,空间复杂度,
以及变位词问题的四种解法,以及内置函数sorted和sort.()的内置函数拓展
不记得的朋友可以点击🔗http://t.csdn.cn/04nTx进行快速定位,接下来进行new knowledge 的学习
后面我们会用来实现各种数据结构
通过运行试验来估计其各种操作运行时间数量级
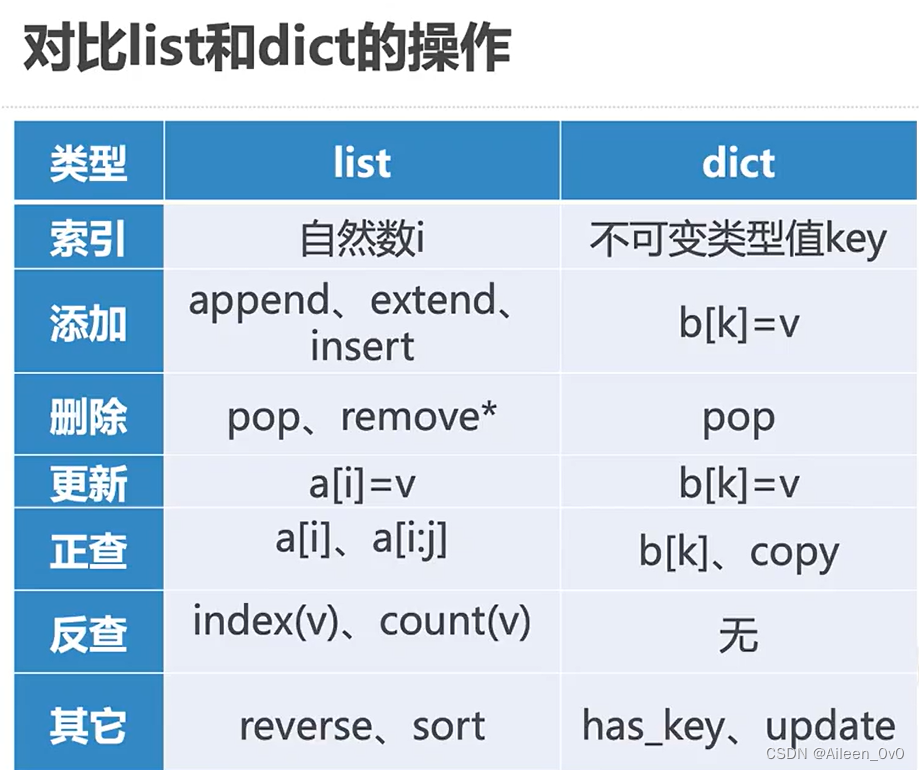
List 列表数据类型常用操作性能🍒
最常用的:按索引取值和赋值( v = a [i]-->取值操作, a [i] = v-->赋值操作)
由于 列表随机访问特性 , 这两个操作执行时间与列表大小无关 , 均为O(1)
另一个是列表增长, 可以选择append() 和 _add_() " + "
lst.append(v), 执行时间 O(1)
lst = lst + [V],列表中加一个列表, 执行时间是O(n+k),其中 k 是被加的列表长度
选择哪个方法来操作列表,决定了程序的性能
4种生成前n个整数列表的方法:
#首先是循环连接列表( + ) 方式生成 def test1():l = []for i in range(1000):l = l + [i]#然后用append方法添加元素生成 def test2():l = []for i in range(1000):l.append(i)#用列表推导式来生成 def test3():l = [i for i in range(1000)]#最后 利用 range函数 调用转成 列表 def test4():l = list(range(1000))

Dict字典数据类型常用操作性能🍌

P、NP、NPC、NP-hard问题详解🫐
想要理解P问题、NP问题、NPC问题、NP-hard问题,需要先弄懂几个概念:
什么是多项式时间(inpolynomial多项式 time)?
什么是确定性算法?什么是非确定性算法?
什么是规约/约化?
1. 多项式时间(Polynomial time)🍈
时间复杂度是衡量算法执行效率的一个指标,它表示算法运行时间与问题规模之间的增长关系。通常用大O符号来表示。
常见的时间复杂度类型有:
- 常数阶 O(1)
- 对数阶 O(log n)
- 线性阶 O(n)
- 线性对数阶 O(n log n)
- 平方阶 O(n^2)
- 立方阶 O(n^3)
- 指数阶 O(2^n)
- 阶乘阶 O(n!)
- 常数时间复杂度 O(1):无论输入的数据规模如何变化,算法的执行时间都是恒定的 示例:访问数组中固定下标的元素,或者执行单次的加减乘除运算等。
- 对数时间复杂度 O(log n):当输入规模增加时,算法执行时间相对于输入规模增加的比率不大。 示例:二分查找算法。
- 线性时间复杂度 O(n):算法执行时间与输入规模是正比的。 示例:遍历一次长度为 n 的数组,或者进行一次循环 从1到n 累加求和等。
- 平方时间复杂度 O(n^2):算法执行时间与输入规模平方成正比。 示例:双重循环嵌套的算法,比如冒泡排序、插入排序等。
- 指数时间复杂度 O(2^n):算法执行时间的增长率与输入规模的指数成正比。 示例:穷举算法,比如求解最长公共子序列问题的暴力算法。
还有其他更高阶的时间复杂度,比如阶乘时间复杂度 O(n!),递归时间复杂度 O(2^n) 等,但是这些复杂度通常不会出现在实际应用中,因为它们的执行时间会随着输入规模的增加而急剧增长,算法的效率非常低下。
像 O(1),O(ln(n)),O(n^a) 等,我们把它叫做多项式级复杂度,因为它的规模n出现在底数的位置;另一种像是 O(a^n) 和 O(n!) 等,它是非多项式级的复杂度,其复杂度计算机往往不能承受。当我们在解决一个问题时,我们选择的算法通常都需要是多项式级的复杂度,非多项式级的复杂度需要的时间太多,往往会超时,除非是数据规模非常小。
2. 确定性算法与非确定性算法🍑
确定性算法:
设A是求解问题B的一个解决算法,在算法的整个执行过程中,每一步都能得到一个确定的解,这样的算法就是确定性算法。
非确定性算法:
设A是求解问题B的一个解决算法,它将问题分解成两部分,分别为猜测阶段和验证阶段,其中
- 猜测阶段:在这个阶段,对问题的一个特定的输入实例x产生一个任意字符串y,在算法的每一次运行时,y的值可能不同,因此,猜测以一种非确定的形式工作。
- 验证阶段:在这个阶段,用一个确定性算法(有限时间内)验证。 ①检查在猜测阶段产生的y是否是合适的形式,如果不是,则算法停下来并得到no; ② 如果y是合适的形式,则验证它是否是问题的解,如果是,则算法停下来并得到yes,否则算法停下来并得到no。它是验证所猜测的解的正确性。
3. 规约/约化🍊
问题A可以约化为问题B,称为“问题A可规约为问题B”,可以理解为问题B的解一定就是问题A的解,因此解决A不会难于解决B。由此可知问题B的时间复杂度一定大于等于问题A。
规约就是选择一个文法规则:X→ABC,依次从栈顶弹出C、B、A,再将X压进栈。规范规约是文法中句子的一个最右推导的逆过程,而最左推导对应的是最右规约 。
再例如《算法导论》中有一个例子:现在有两个问题:求解一个一元一次方程和求解一个一元二次方程。那么我们说,前者可以规约为后者,意即知道如何解一个一元二次方程那么一定能解出一元一次方程。我们可以写出两个程序分别对应两个问题,那么我们能找到一个“规则”,按照这个规则把解一元一次方程程序的输入数据变一下,用在解一元二次方程的程序上,两个程序总能得到一样的结果。这个规则即是:两个方程的对应项系数不变,一元二次方程的二次项系数为0。
从规约的定义中我们看到,一个问题规约为另一个问题,时间复杂度增加了,问题的应用范围也增大了。通过对某些问题的不断规约,我们能够不断寻找复杂度更高,但应用范围更广的算法来代替复杂度虽然低,但只能用于很小的一类问题的算法。存在这样一个NP问题,所有的NP问题都可以约化成它。换句话说,只要解决了这个问题,那么所有的NP问题都解决了。这种问题的存在难以置信,并且更加不可思议的是,这种问题不只一个,它有很多个,它是一类问题。这一类问题就是传说中的NPC问题,也就是NP-完全问题。
4. P类问题、NP类问题、NPC问题、NP难问题🍍
P类问题:
It is the set of problems which can be solved by some algorithms inpolynomial time. --->能在多项式时间内可解的问题.
故事案例🌰:
柯尼斯堡七桥问题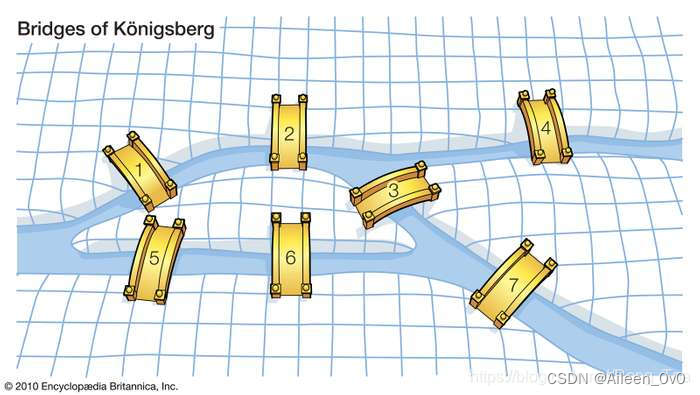
18世纪初普鲁士的哥尼斯堡,有一条河穿过,河上有两个小岛,有七座桥把两个岛与河岸联系起来(如右上图)。有个人提出一个问题:一个步行者怎样才能不重复、不遗漏地一次走完七座桥,最后回到出发点。后来大数学家欧拉把它转化成一个几何问题(如左图下)——一笔画问题。他不仅解决了此问题,且给出了连通图可以一笔画的充要条件是:
⒈任意点连接的边数为偶数
⒉拥有奇数边点的个数为2或0.
⒊其他情况的图都不能一笔画出。(奇点数除以二便可算出此图需几笔画成。)
一起来玩游戏吧~
判断下图能否一笔画:
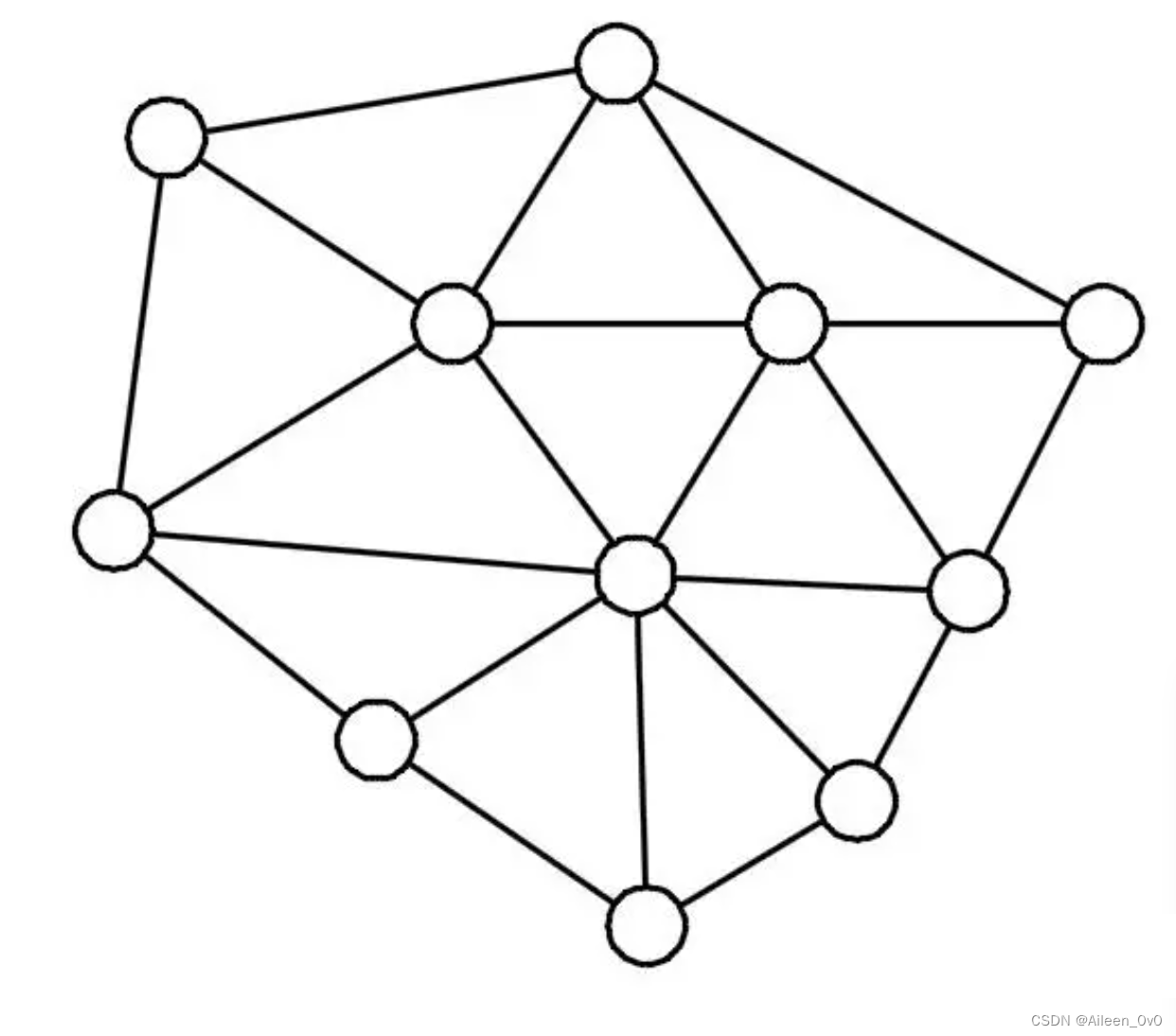
答案是没有解,因为只有当拥有奇数条边的顶点数量小于或者等于2个时才会有解,而图中有8个粉红色顶点有奇数条边,所以无解。
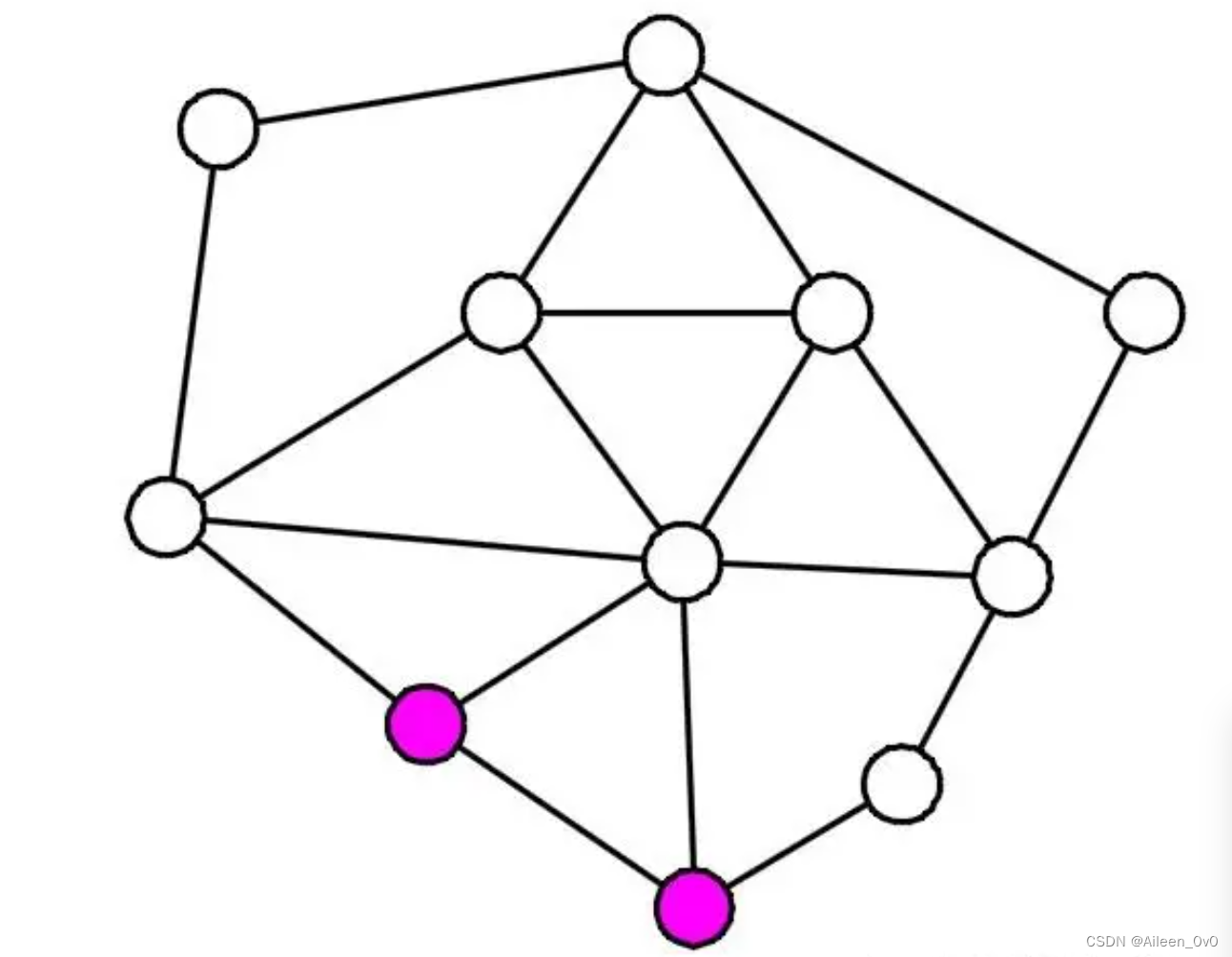
有解
NP类问题:
lt is the set of problems which are not sure whether it can be solved bysome algorithms in polynomial time. But it is possible to verify the answer in polynomial time. --->不确定可以在多项式时间内解决的问题.在多项式时间内“可验证”的问题。也就是说,不能判定这个问题到底有没有解,而是猜出一个解来在多项式时间内证明这个解是否正确。即该问题的猜测过程是不确定的,而对其某一个解的验证则能够在多项式时间内完成。P类问题属于NP问题,但NP类问题不一定属于P类问题。
故事案例🌰:
1859 年,爱尔兰数学家哈密尔顿(Hamilton)提出了一个“周游世界”的游戏
下图中(a),哈密顿提出的「周游世界」的游戏。把一个正十二面体的二十个顶点看成地球上的二十个城市。要求游戏者沿棱线走,寻找一条经过所有结点一次且仅一次的回路,(b)是其哈密顿图,哈密顿回路由实线标出。
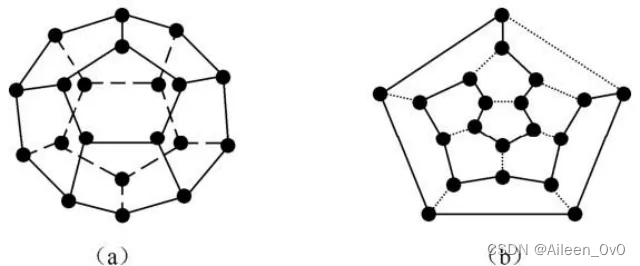
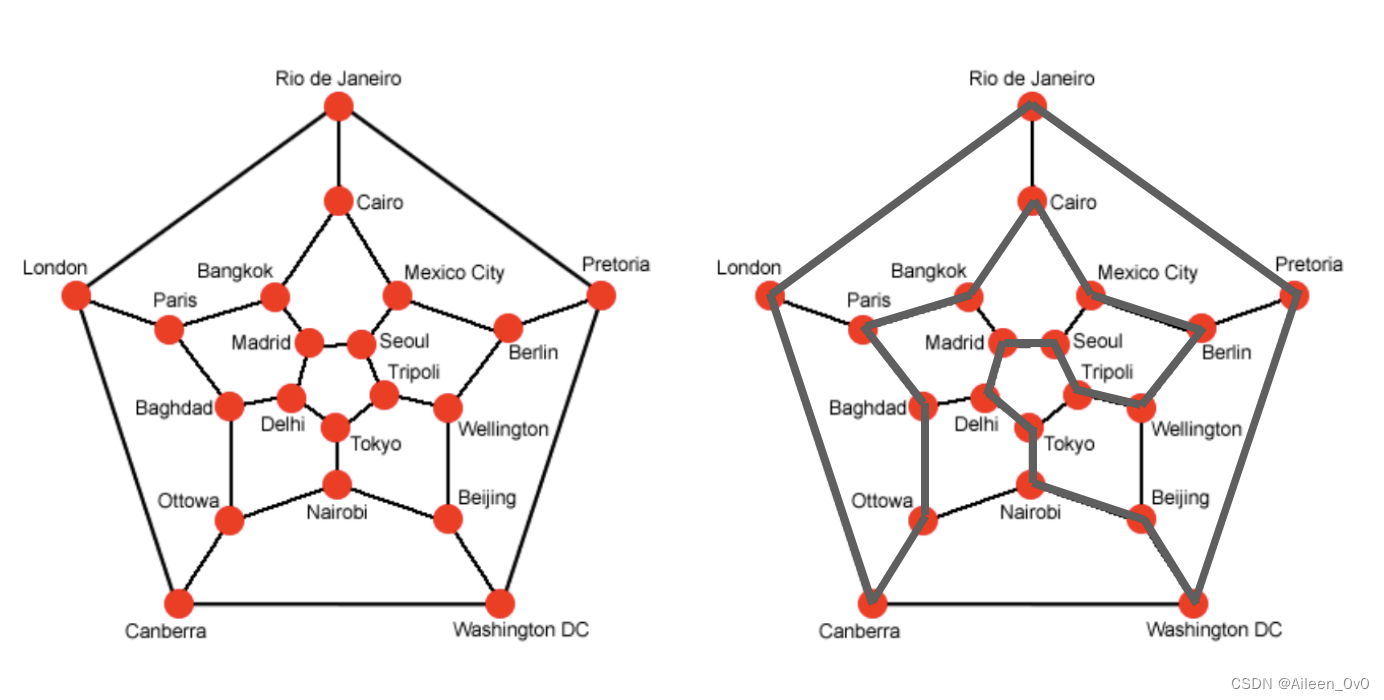
简而言之,哈密尔顿回路是指,从图中的一个顶点出发,沿着边行走,经过图的每个顶点,且每个顶点仅访问一次,之后再回到起始点的一条路径。如上图所示,我们的起始点选定为 Washington DC,灰色实线构成的一条路径就是一条哈密尔顿回路。
在图论算法的领域中,哈密尔顿回路(Hamilton Loop)和路径(Hamilton Path)在定义上是有所区分的:
哈密尔顿回路(Hamilton Loop)要求从起始点出发并能回到起始点,其路径是一个环。
哈密尔顿路径(Hamilton Path)并不要求从起始点出发能够回到起始点,也就是说:起始顶点和终止顶点之间不要求有一条边。
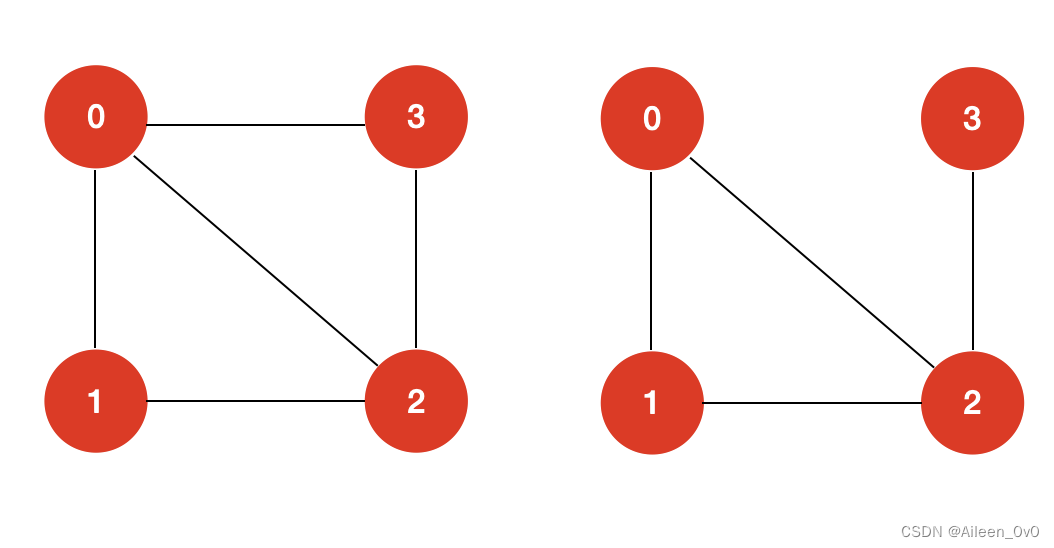
比如上面这两个图,左图既存在哈密尔顿回路,也存在哈密尔顿路径。而右图只存在哈密尔顿路径,并不存在哈密尔顿回路。
如何求解一个图是否存在哈密尔顿回路呢?
一个最直观的想法就是暴力求解。暴力求解的思路也很简单:我们遍历图的每一个顶点 v,然后从顶点 v 出发,看是否能够找到一条哈密尔顿回路。
暴力求解和求解全排列问题是等价的,其时间复杂度为 O ( N ! ) ,N 为图的顶点的个数。
O ( N ! ) 是一个非常高的复杂度,它并不是一个多项式级别的复杂度。像 O ( 1 ) , O(NlogN),O(N^2)这些我们常见的复杂度都是多项式级的复杂度,而O(a^N),O ( N ! )这些复杂度是非多项式级的,也就是说,在数据量 N 极大的情况下,我们的现代计算机是不能承受的。
那么除了暴力求解哈密尔顿回路问题,是否存在更好的算法?
很遗憾的是,对于哈密尔顿问题,目前并没有多项式级别的算法。我们只能在暴力破解的基础上,尽量去做到更多的优化,譬如回溯剪枝,记忆化搜索等,但是,还没有找到一种多项式级别的算法来解决哈密尔顿问题。
通常,这类问题也被称为 NP(Non-deterministic Polynomial)难问题。
NPC问题(NP-complete):
they are the problems which are the hardest in NP. If they can be solved in polynomial time, all NP problem can be solved inpolynomial time.存在这样一个NP问题,所有的NP问题都可以约化成它。换句话说,只要解决了这个问题,那么所有的NP问题都解决了。其定义要满足2个条件:
- 它是一个NP问题;
- 所有NP问题都能规约到它。
故事案例🌰:
设有p个城镇,已知每两个城镇之间的距离,一个售货员从某一城镇出发巡回售货,问这个售货员应如何选择路线,能使每个城镇经过一次且仅一次,最后返回到出发地,而使总的行程最短?这个问题称为旅行售货员问题。 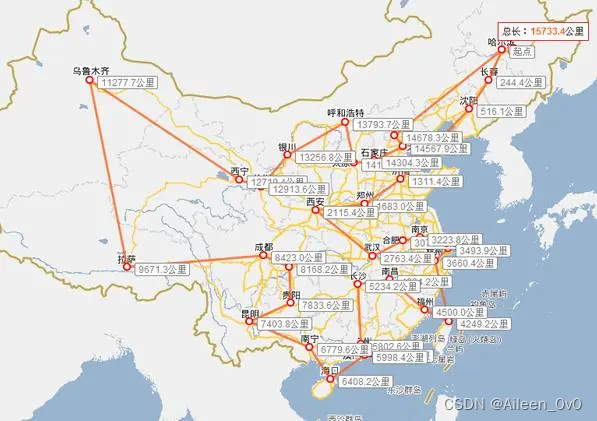
NP难问题:
NP-Hard问题是这样一种问题,它满足NPC问题定义的第二条但不一定要满足第一条(就是说,NP-Hard问题要比 NPC问题的范围广,NP-Hard问题没有限定属于NP),即所有的NP问题都能约化到它,但是他不一定是一个NP问题。NP-Hard问题同样难以找到多项式的算法,但它不列入我们的研究范围,因为它不一定是NP问题。即使NPC问题发现了多项式级的算法,NP-Hard问题有可能仍然无法得到多项式级的算法。事实上,由于NP-Hard放宽了限定条件,它将有可能比所有的NPC问题的时间复杂度更高从而更难以解决
上面四个问题的关系图: 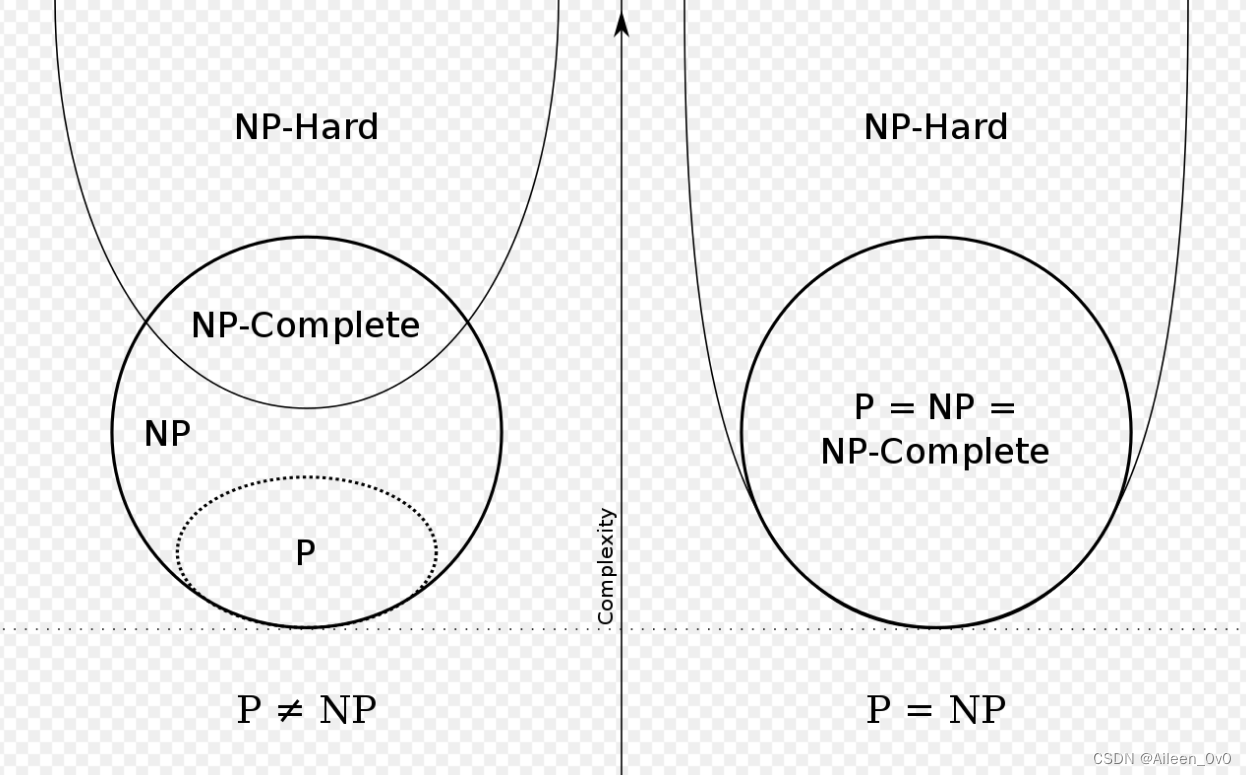
🐻今天的内容就分享到这里啦~🐻
🐻喜欢就三连一下呗~🐻
🐻感谢支持💖!🐻

相关文章:

数据结构与算法基础-(3)
🌈write in front🌈 🧸大家好,我是Aileen🧸.希望你看完之后,能对你有所帮助,不足请指正!共同学习交流. 🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如…...
maven中relativepath标签的含义
一 relative标签的含义 1.1 作用 这个<parent>下面的<relativePath>属性:parent的pom文件的路径。 relativePath 的作用是为了找到父级工程的pom.xml;因为子工程需要继承父工程的pom.xml文件中的内容。然后relativePath 标签内的值使用相对路径定位…...

Greenplum 对比 Hadoop
Greenplum属于MPP架构,和Hadoop一样都是为了解决大规模数据的并行计算而出现的技术,两者的相似点在于: 分布式存储,数据分布在多个节点服务器上分布式并行计算框架支持横向扩展来提高整体的计算能力和存储容量都支持X86开放集群架…...

OJ练习第182题——字典树(前缀树)
字典树(前缀树) 208. 实现 Trie (前缀树)题目描述示例知识补充官解代码 211. 添加与搜索单词 - 数据结构设计题目描述示例思路Java代码 208. 实现 Trie (前缀树) 力扣链接:208. 实现 Trie (前缀树) 题目描述 示例 知识补充 插入字符串 我…...

前端知识总结
在前端开发中,y x是一种常见的自增运算符的使用方式。它表示将变量x的值自增1,并将自增后的值赋给变量y。 具体来说,x是一种后缀自增运算符,表示将变量x的值自增1。而y x则是将自增前的值赋给变量y。这意味着在执行y x之后&am…...
)
中国JP-10燃料行业市场研究与预测报告(2023版)
内容简介: 高密度燃料是指以石油基、煤基和生物质基烃类为原料,通过聚合、加氢、异构等工艺合成的密度大于0.85 gcm-3的饱和多环碳氢化合物,广泛应用于航空航天领域。由于高密度燃料密度大和体积热值高等特点,飞行器在油箱体积一…...

护眼灯显色指数应达多少?眼科医生推荐灯光显色指数多少合适
台灯的显色指数是其非常重要的指标,它可以表示灯光照射到物体身上,物体颜色的真实程度,一般用平均显色指数Ra来表示,Ra值越高,灯光显色能力越强。常见的台灯显色指数最低要求一般是在Ra80以上即可,比较好的…...

AI 大模型
随着人工智能技术的迅猛发展,AI 大模型逐渐成为推动人工智能领域提升的关键因素,大模型已成为了引领技术浪潮研究和应用方向。大模型即大规模预训练模型,通常是指那些在大规模数据上进行了预训练的具有庞大规模和复杂结构的人工智能模型&…...

一个案例熟悉使用pytorch
文章目录 1. 完整模型的训练套路1.2 导入必要的包1.3 准备数据集1.3.1 使用公开数据集:1.3.2 获取训练集、测试集长度:1.3.3 利用 DataLoader来加载数据集 1.4 搭建神经网络1.4.1 测试搭建的模型1.4.2 创建用于训练的模型 1.5 定义损失函数和优化器1.6 使…...
)
MySQL - limit 分页查询 (查询操作 五)
功能介绍:分页查询(limit)是一种常用的数据库查询技术,它允许我们从数据库表中按照指定的数量和顺序获取数据,它在处理大量数据时特别有用,可以提高查询效率并减少网络传输的数据 语法:SELECT …...
代码随想录笔记--动态规划篇
1--动态规划理论基础 动态规划经典问题:① 背包问题;② 打家劫舍;③ 股票问题; ④ 子序列问题; 动态规划五部曲: ① 确定 dp 数组及其下标的含义; ② 确定递推公式; ③ 确定 dp 数组…...

vue之vuex
Vuex 是 Vue.js 的一个状态管理模式和库,为应用中的所有组件提供了一个集中式的存储管理,并提供了一种强大的方式来管理应用的状态。Vuex 包含以下核心概念: State:定义了应用的状态,类似于组件中的 data。 Getters&a…...
)
ISO 26262 系列学习笔记 ———— ASIL定义(Automotive Safety Integration Level)
文章目录 介绍严重度(Severity)暴露概率(Probability of Exposure)可控性(Controllability) 介绍 如果没有另行说明,则应满足ASIL A、B、C和D各分条款的要求或建议。这些要求和建议参考了安全目…...

代码随想录 第8章 二叉树
1、理论知识 (1)、满二叉树 如果一棵二叉树只有度为0的节点和度为2的节点,并且度为0的节点在同一层上,则这棵二叉树为满二叉树。 (2)、完全二叉树 除了底层节点可能没有填满,其余每层的节点…...
计算机网络工程师多选题系列——计算机网络
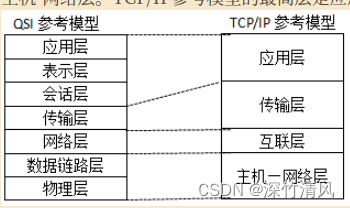
2 计算机网络 2.1 网络技术基础 题型1 TCP/IP与ISO模型的问题 TCP/IP由IETF制定,ISO由OSI制定; TCP/IP分为四层,分别是主机-网络层、互联网络层、传输层和应用层;OSI分为七层,分别是物理层、数据链路层、网络层(实…...
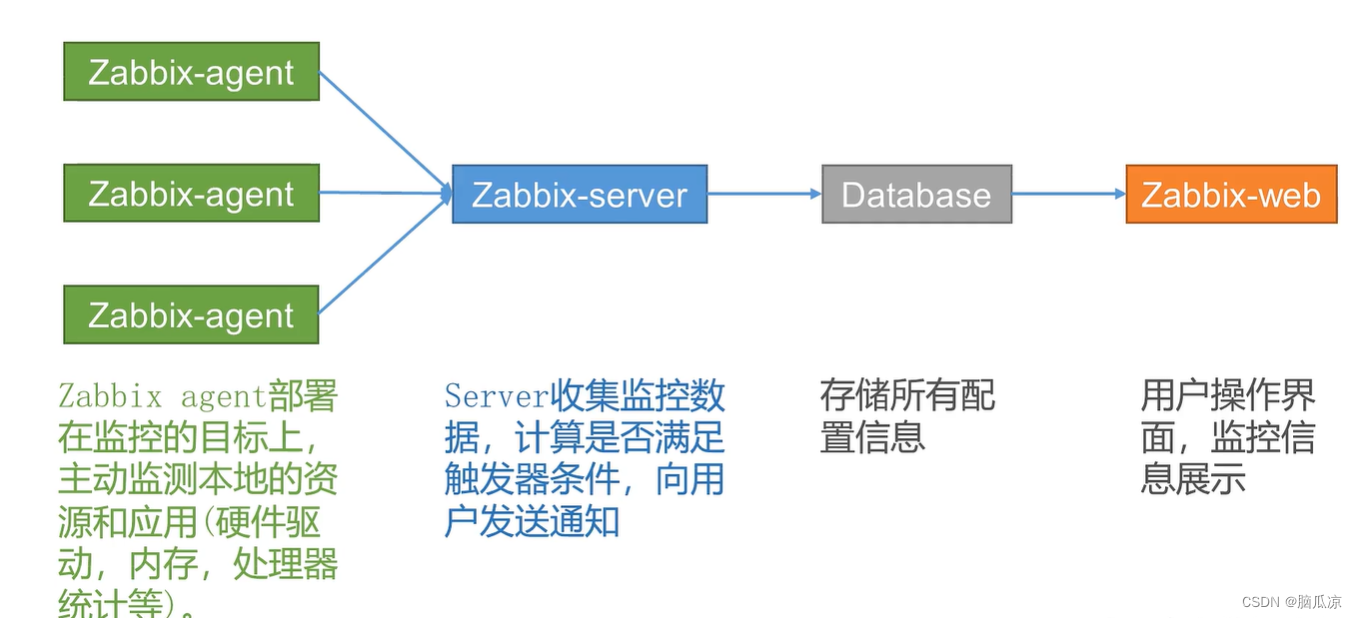
Zabbix5.0_介绍_组成架构_以及和prometheus的对比_大数据环境下的监控_网络_软件_设备监控_Zabbix工作笔记001
z 这里Zabbix可以实现采集 存储 展示 报警 但是 zabbix自带的,展示 和报警 没那么好看,我们可以用 grafana进行展示,然后我们用一个叫睿象云的来做告警展示, 会更丰富一点. 可以看到 看一下zabbix的介绍. 对zabbix的介绍,这个zabbix比较适合对服务器进行监控 这个是zabbix的…...
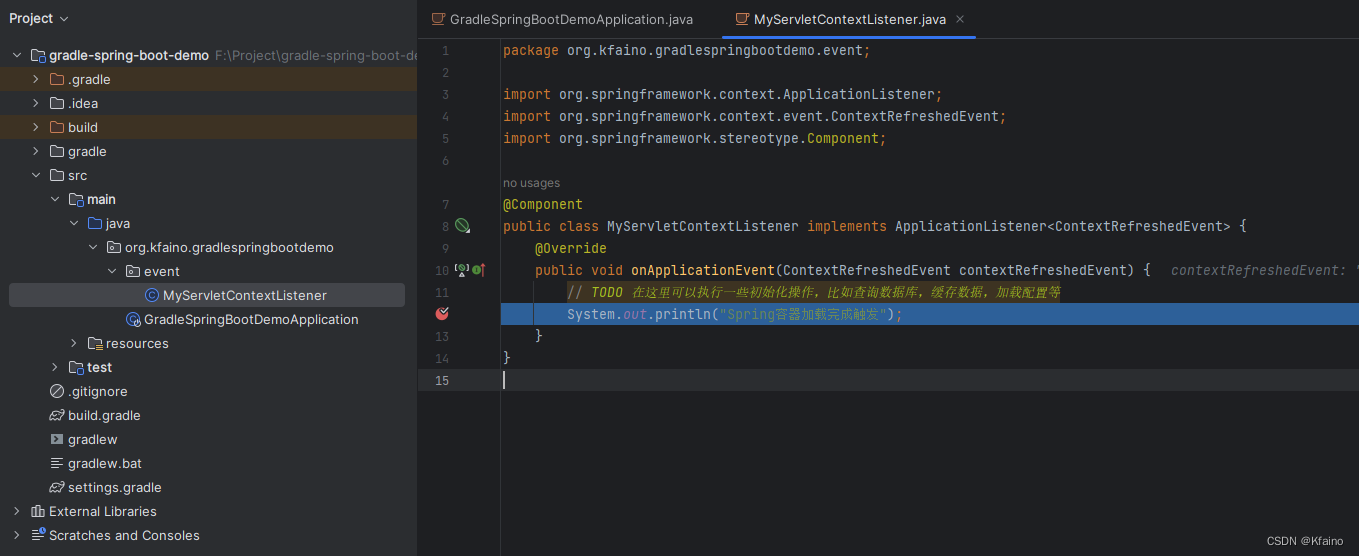
Spring | 事件监听器应用与最佳实践
引言 在复杂的软件开发环境中,组件之间的通信和信息交流显得尤为重要。Spring框架,作为Java世界中最受欢迎的开发框架之一,提供了一种强大的事件监听器模型,使得组件间的通信变得更加灵活和解耦。本文主要探讨Spring事件监听器的…...

正点原子lwIP学习笔记——NETCONN接口简介
1. NETCONN接口简介 NETCONN API 使用了操作系统的 IPC 机制, 对网络连接进行了抽象,使用同一的接口完成UDP和TCP连接。 NETCONN API接口是在RAW接口基础上延申出来的一套API接口 首先会调用netconn_new创建一个pcb控制块,其实际是一个宏定…...
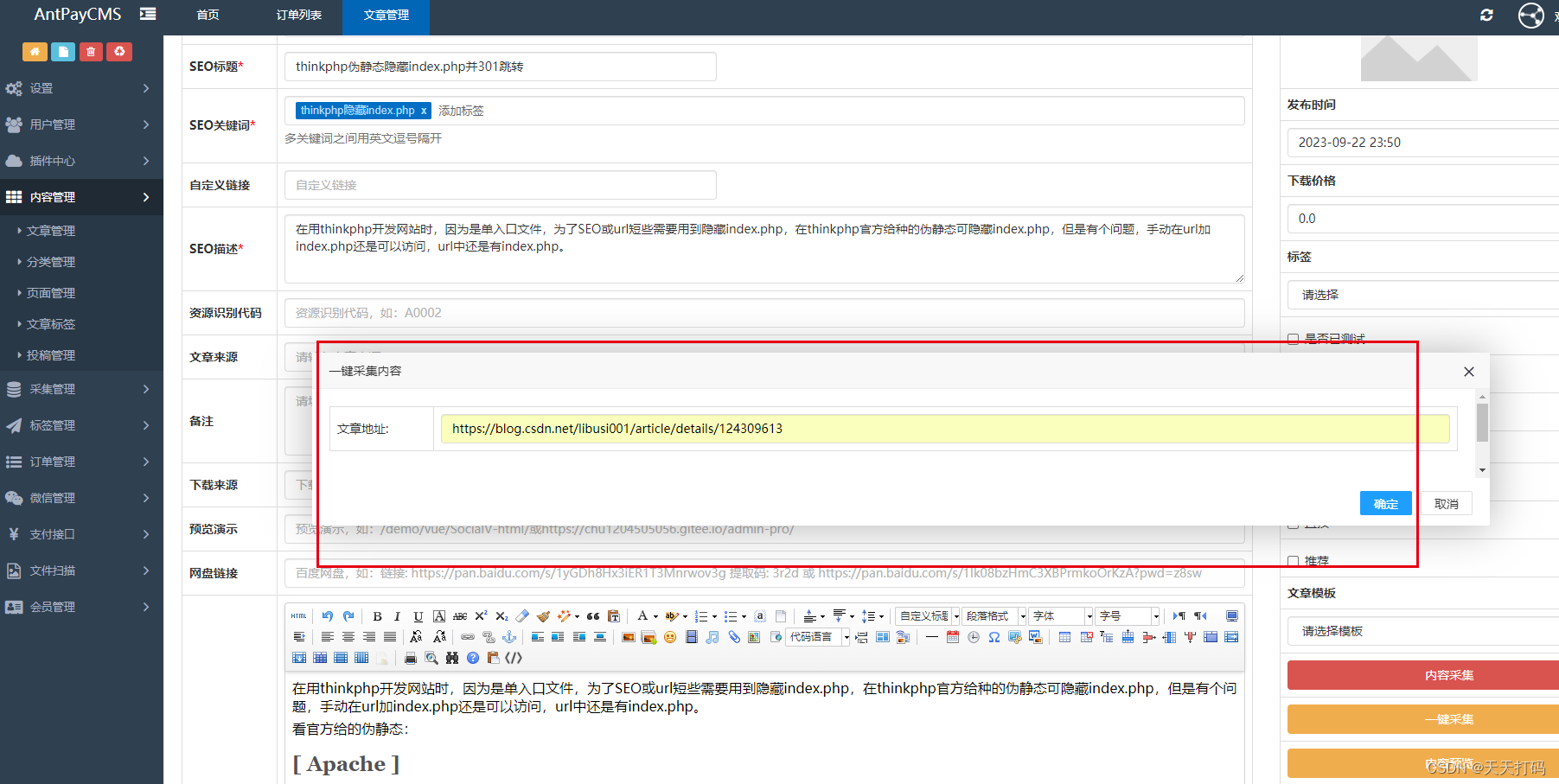
PHP自动识别采集何意网址文章正文内容
在做PHP采集内容时,用过querylist采集组件,但是这个插件采集页面内容时,都必须要写个采集选择器。这样比较麻烦,每个文章页面都必须指定一条采集规则 。就开始着手找一个插件可以能自动识别任意文章url正文内容并采集的࿰…...

区块链实验室(27) - 区块链+物联网应用案例
分享最新的区块链物联网应用案例:HPCLS-BC...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...
