第九章 动态规划 part11 123. 买卖股票的最佳时机III 188. 买卖股票的最佳时机IV
第五十天| 第九章 动态规划 part11 123. 买卖股票的最佳时机III 188. 买卖股票的最佳时机IV
一、123. 买卖股票的最佳时机III==(难难难难难)==
-
题目链接:https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iii/
-
题目介绍:
-
给定一个数组,它的第
i个元素是一支给定的股票在第i天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成两笔交易。
**注意:**你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:prices = [3,3,5,0,0,3,1,4] 输出:6 解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。
-
-
思路:
-
注意:本题是最多买卖两次股票
-
DP五部曲:
-
(1)确定dp数组及下标含义:
-
一天一共就有五个状态,
- 没有操作 (其实我们也可以不设置这个状态)
- 第一次持有股票
- 第一次不持有股票
- 第二次持有股票
- 第二次不持有股票
-
dp[i][j]中 i表示第i天,j为 [0 - 4] 五个状态,dp[i][j]表示第i天状态j所剩最大现金。 -
五个状态分别如下:
-
dp[i][0]: 表示第i天,不操作股票的时候,手中的最大金额(也就是0) dp[i][1]: 表示第i天,第一次持有该股票,手中的最大金额 dp[i][2]: 表示第i天,第一次不持有该股票,手中的最大金额 dp[i][3]: 表示第i天,第二次持有该股票,手中的最大金额 dp[i][4]: 表示第i天,第二次不持有该股票,手中最大的金额
-
-
-
(2)确定递推公式:
-
和I、II一样的思路
-
dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0]-prices[i]); dp[i][2] = Math.max(dp[i-1][2], dp[i-1][1]+prices[i]); dp[i][3] = Math.max(dp[i-1][3], dp[i-1][2]-prices[i]); dp[i][4] = Math.max(dp[i-1][4], dp[i-1][3]+prices[i]);
-
-
(3)初始化dp数组:
-
dp[0][0] = 0; dp[0][1] = -prices[0]; dp[0][2] = 0; dp[0][3] = -prices[0]; dp[0][4] = 0; -
分别表示的含义是: (1)dp[0][0]:第0天,没有任何操作手里的金额是0 (2)dp[0][1]:第0天,第一次持有股票,手里的金额就是买第0天的股票花掉的 (3)dp[0][2]:第0天,第一次不持有股票,手里的金额就是买完再卖了第0天的股票,也就是0 (4)dp[0][3]:为什么会出现第二次持有呢?可以当作第一天买了又卖了,然后再买 (5)dp[0][4]:同理。
-
-
(4)确定遍历顺序:
- 正序
-
(5)打印dp数组:
-
-
-
代码:
class Solution {public int maxProfit(int[] prices) {if (prices == null || prices.length == 0) return 0;// (1)确定dp数组及下标含义// dp[i][0]: 表示第i天,不操作股票的时候,手中的最大金额(也就是0)// dp[i][1]: 表示第i天,第一次持有该股票,手中的最大金额// dp[i][2]: 表示第i天,第一次不持有该股票,手中的最大金额// dp[i][3]: 表示第i天,第二次持有该股票,手中的最大金额// dp[i][4]: 表示第i天,第二次不持有该股票,手中最大的金额int[][] dp = new int[prices.length][5];// (3)初始化dp数组dp[0][1] = -prices[0];dp[0][3] = -prices[0];// (4)确定遍历顺序for (int i = 1; i < prices.length; i++) {// (2)确定递推公式dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0]-prices[i]);dp[i][2] = Math.max(dp[i-1][2], dp[i-1][1]+prices[i]);dp[i][3] = Math.max(dp[i-1][3], dp[i-1][2]-prices[i]);dp[i][4] = Math.max(dp[i-1][4], dp[i-1][3]+prices[i]);}return dp[prices.length-1][4];}
}
- 注意:
- 这里的返回值再强调一下:
- 首先众所周知,你不持有股票手里的金额一定是大于持有股票的,所以返回的状态一定是偶数状态。
- 那为什么不返回状态2呢?
- 是因为状态4其实是包含了状态2的,因为如果状态2达到最大值,状态4一定会保持这个最大值的。因此直接返回状态4即可。
- 这里的返回值再强调一下:
二、188. 买卖股票的最佳时机IV
-
题目链接:https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iv/
-
题目介绍:
-
给你一个整数数组
prices和一个整数k,其中prices[i]是某支给定的股票在第i天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成
k笔交易。也就是说,你最多可以买k次,卖k次。**注意:**你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:k = 2, prices = [2,4,1] 输出:2 解释:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。
-
-
思路:
- 注意:本题是最多买卖k次股票
- 根据上道题可以推算出本题,只需要把握一些关键的边界点即可
- (1)dp数组的初始化长度:2k+1
- (2)初始化dp数组:奇数状态初始为-prices[0],边界是< 2 * k
- (3)递推公式:需要一个j表示状态,j从0开始,每次循环+2,因此到最后一位2k时,j=2k-2。因此j的边界是:j < 2k - 1;
-
代码:
class Solution {public int maxProfit(int k, int[] prices) {if (prices == null || prices.length == 0) return 0;int[][] dp = new int[prices.length][2*k+1];for (int i = 1; i < 2*k; i += 2) {dp[0][i] = -prices[0];}for (int i = 1; i < prices.length; i++) {for (int j = 0; j < 2*k-1; j += 2) {dp[i][j + 1] = Math.max(dp[i-1][j+1], dp[i-1][j] - prices[i]);dp[i][j + 2] = Math.max(dp[i-1][j+2], dp[i-1][j+1] + prices[i]);}}return dp[prices.length - 1][2*k];}
}
相关文章:

第九章 动态规划 part11 123. 买卖股票的最佳时机III 188. 买卖股票的最佳时机IV
第五十天| 第九章 动态规划 part11 123. 买卖股票的最佳时机III 188. 买卖股票的最佳时机IV 一、123. 买卖股票的最佳时机III(难难难难难) 题目链接:https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iii/ 题目介绍ÿ…...
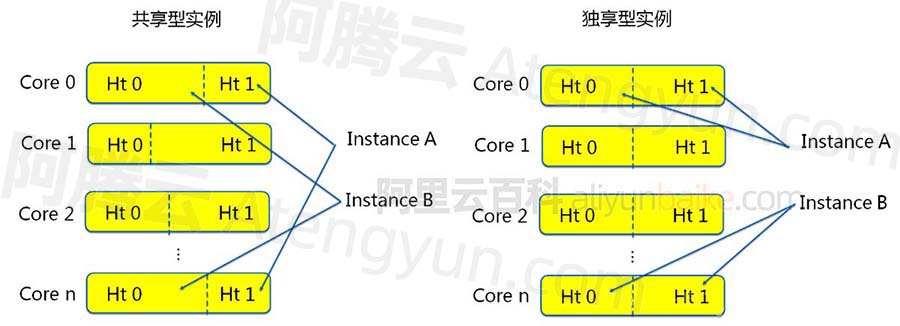
阿里云服务器共享型和企业级独享有什么区别?
阿里云ECS云服务器共享型和企业级有什么区别?企业级就是独享型,共享型和企业级云的主要区别CPU调度模式,共享型是非绑定CPU调度模式,企业级是固定CPU调度模式,共享型云服务器在高负载时计算性能可能出现波动不稳定&…...

Vue.js基本语法上
🎬 艳艳耶✌️:个人主页 🔥 个人专栏 :《Spring与Mybatis集成整合》《springMvc使用》 ⛺️ 生活的理想,为了不断更新自己 ! 目录 1.插值 1.1 文本 1.2 v-v-html 1.3 数据双向绑定数据(v-model) 1.4 属性ÿ…...

【1333. 餐厅过滤器】
来源:力扣(LeetCode) 描述: 给你一个餐馆信息数组 restaurants,其中 restaurants[i] [idi, ratingi, veganFriendlyi, pricei, distancei]。你必须使用以下三个过滤器来过滤这些餐馆信息。 其中素食者友好过滤器 v…...

wifi7有关的210个提案
[1] TGbe, “Compendium of motions related to the contents of the TGbe specification framework document,” 19/1755r8, September 2020. [2] Bin Tian (Qualcomm), “Discussion on 11be PHY capabilities,” 20/0975r0, July 2020. [3] TGbe, “Compendiu…...
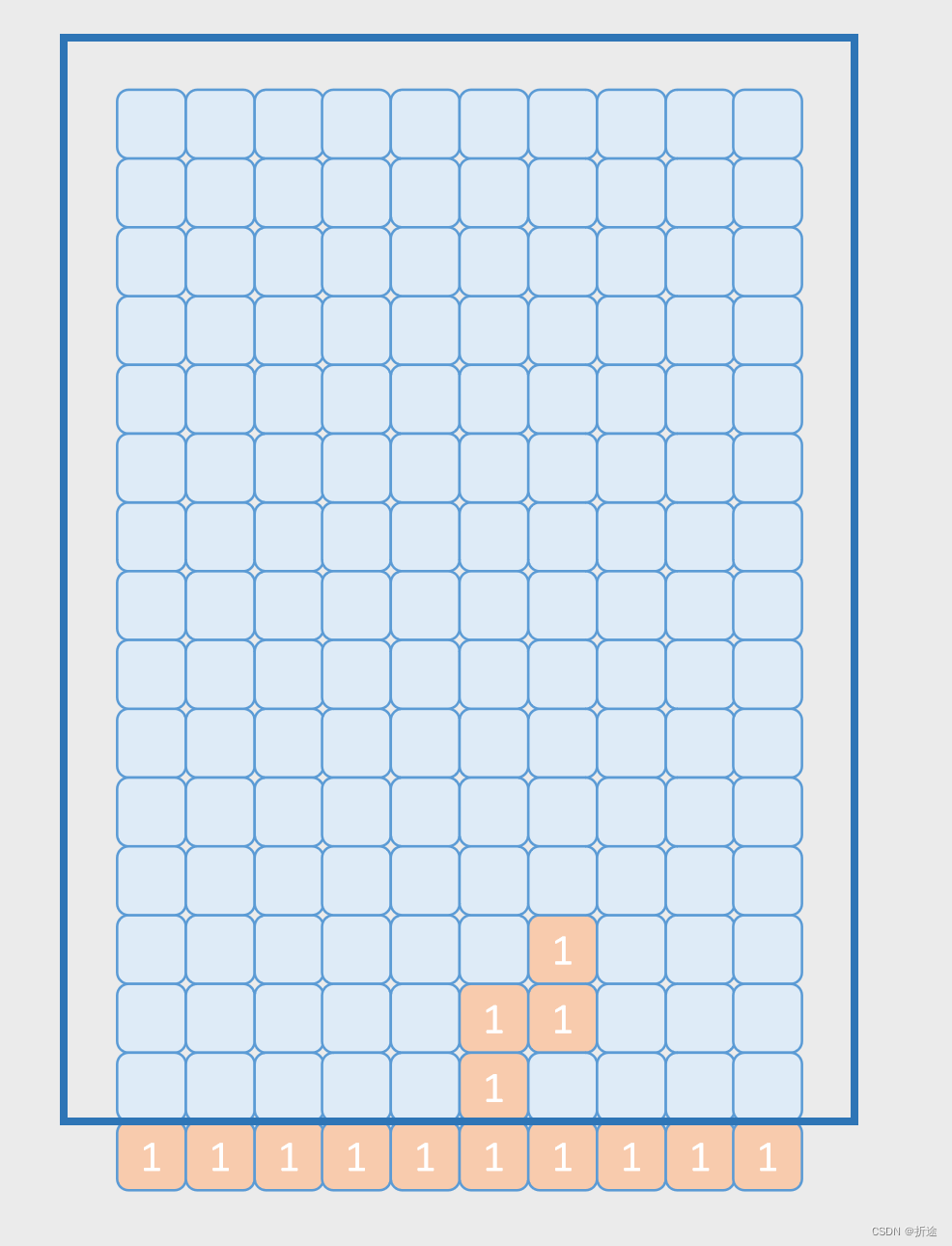
200行C++代码写一个Qt俄罗斯方块小游戏
小小演示一下: 大体思路: 其实很早就想写一个俄罗斯方块了,但是一想到那么多方块还要变形,还要判断落地什么的就脑壳疼。直到现在才写出来。 俄罗斯方块这个小游戏的小难点其实就一个,就是方块的变形,看似…...

蓝桥杯每日一题20223.9.26
4407. 扫雷 - AcWing题库 题目描述 分析 此题目使用map等都会超时,所以我们可以巧妙的使用哈希模拟散列表,哈希表初始化为-1首先将地雷读入哈希表,找到地雷的坐标在哈希表中对应的下标,如果没有则此地雷的位置第一次出现&#…...
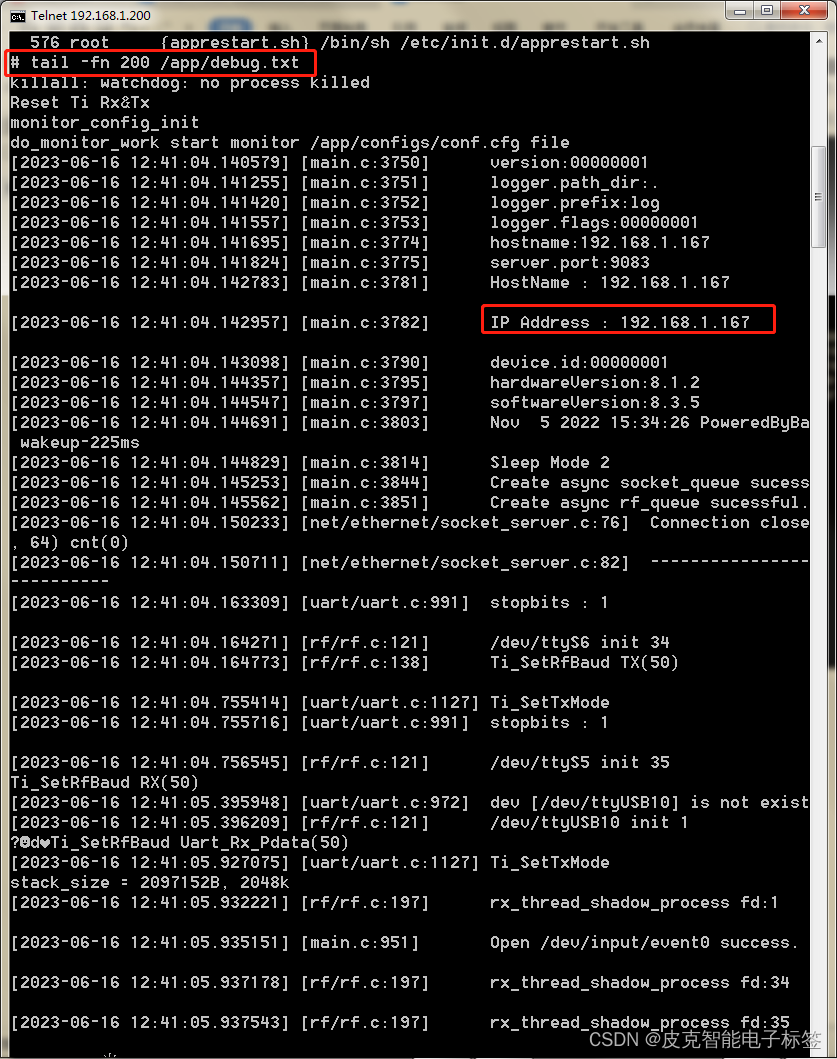
查看基站后台信息
查看基站后台信息 电脑配置固定ip: 192.168.1.99: 打开“网络和共享中心”,选择更改适配器设置: 右键“本地连接”,选择属性 基站网线直连电脑网口 Telnet 登录基站 打开dos窗口 windows键R”,输入cmd,点确定&…...

关于坐标的旋转变换和坐标系的旋转变换
不管是坐标的旋转变换还是坐标系下的旋转变换,只和旋转的顺时针和逆时针有关。然坐标系间的顺时针和逆时针是根据当前坐标系在目标坐标系下的相对位置确定。 一。逆时针旋转belta角度的公式 二。顺时针旋转belta角度的公式 三。坐标的旋转变换 1.坐标的旋转变换相…...
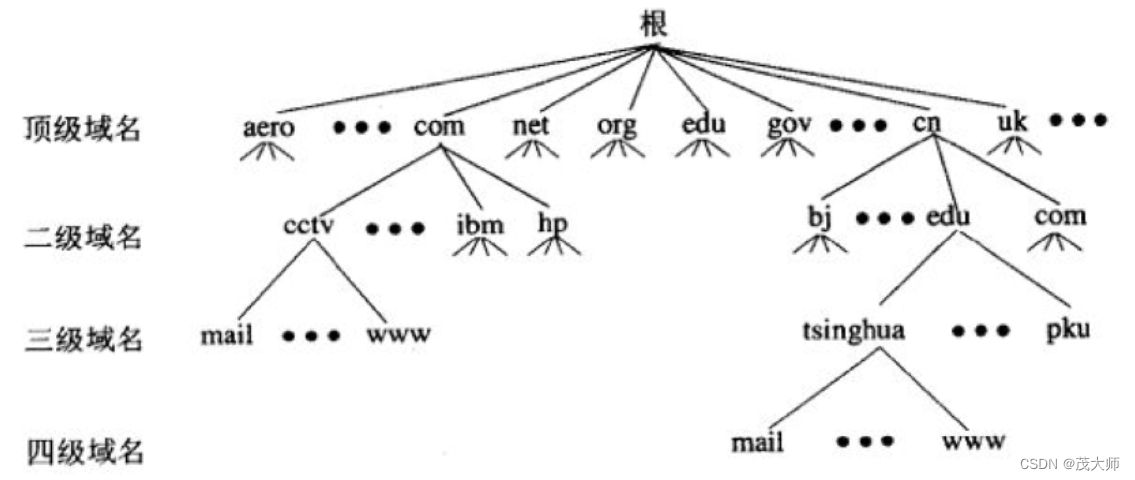
2023.9.19 关于 数据链路层 和 DNS 协议 基本知识
目录 数据链路层 MTU DNS 协议 补充 DHCP协议 数据链路层 基本概念: 考虑相邻两个节点之间的传输(通过 网线 / 光纤 / 无线 直接相连的两个设备)以太网协议 规定了 数据链路层 和 物理层 的内容 IP地址 与 mac地址 的相互配合 IP地址 描…...

如何保证接口幂等性
简介 接口幂等性就是说用户使用相同的参数请求同一个接口无论是一次还是多次都应该是一样的。不会因为多次的点击产生不同效果。 举个栗子:一个用户在手机APP上提200块钱,然后一不小心点击了两次,那么就应该只提取出200块钱,不应…...
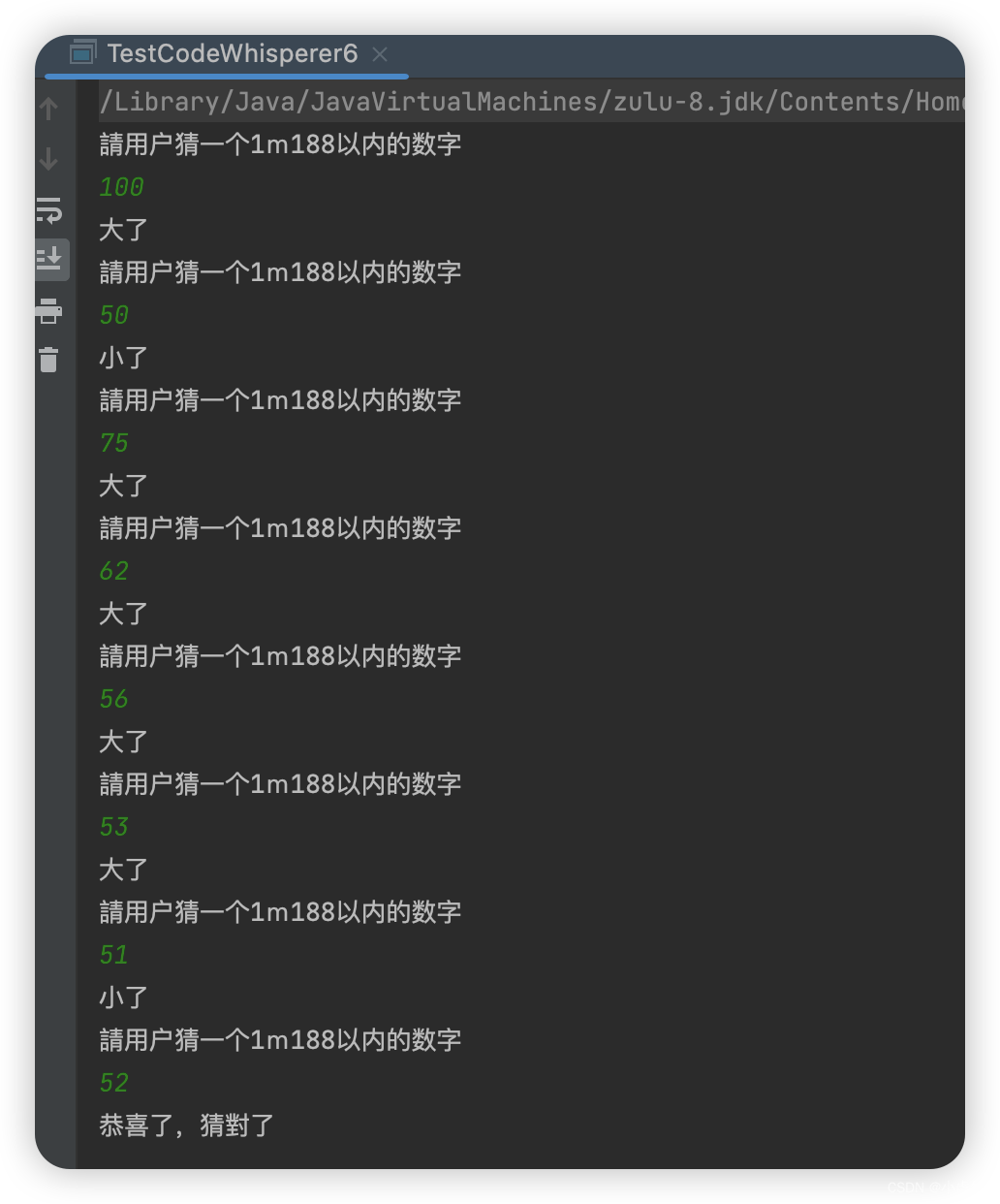
搭建智能桥梁,Amazon CodeWhisperer助您轻松编程
零:前言 随着时间的推移,人工智能技术以惊人的速度向前发展,正掀起着全新的编程范式革命。不仅仅局限于代码生成,智能编程助手等创新应用也进一步提升了开发效率和代码质量,极大地推动着软件开发领域的快速繁荣。 当前…...
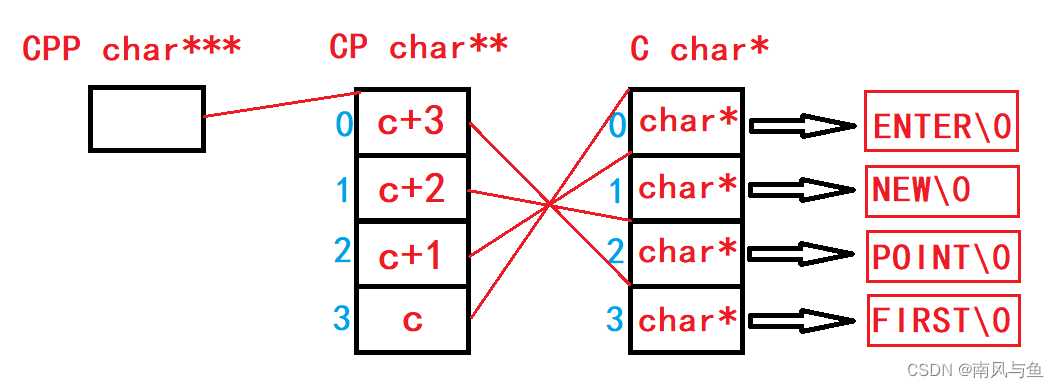
数组和指针笔试题解析之【指针】
目录 🍂笔试题1: 🍂笔试题2: 🍂笔试题3: 🍂笔试题4: 🍂笔试题5: 🍂笔试题6: 🍂笔试题7: 🍂笔试题…...
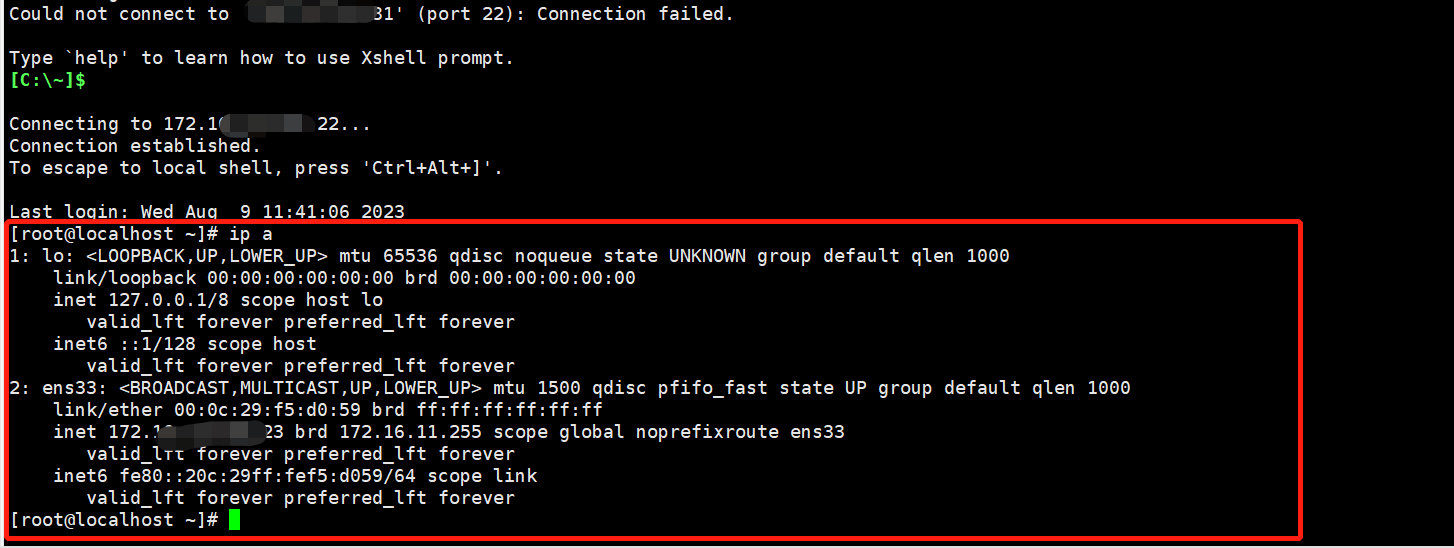
【Linux】之Centos7卸载KVM虚拟化服务
👨🎓博主简介 🏅云计算领域优质创作者 🏅华为云开发者社区专家博主 🏅阿里云开发者社区专家博主 💊交流社区:运维交流社区 欢迎大家的加入! 🐋 希望大家多多支…...
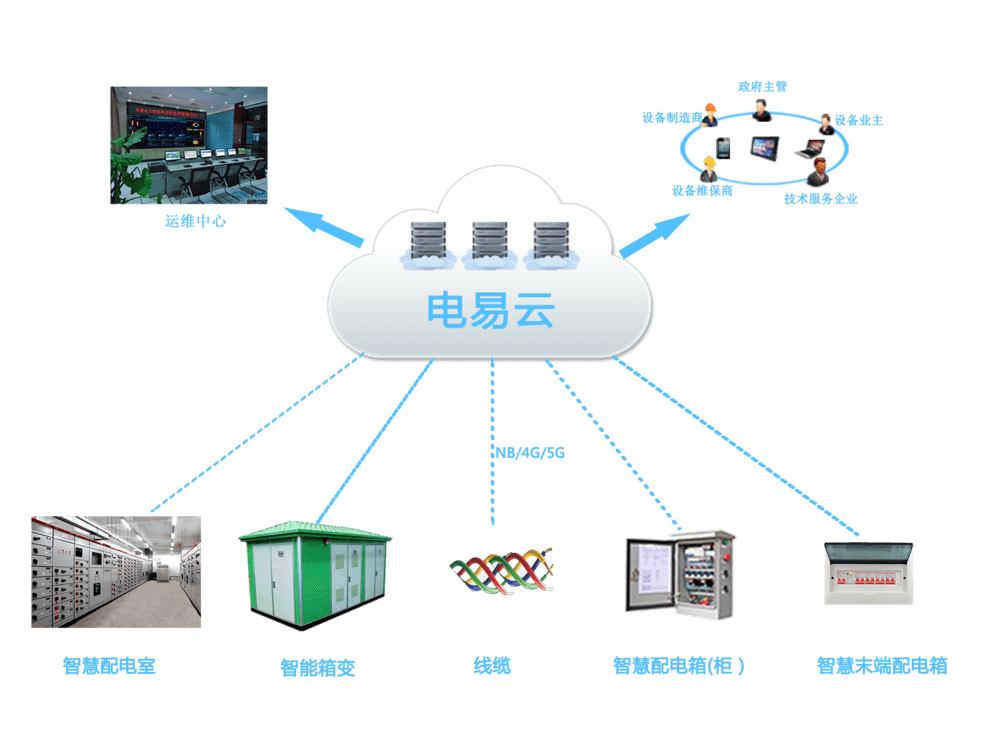
智能电力运维系统:数字化转型在电力行业的关键应用
随着信息技术、人工智能等的飞速发展,数字化改造已成为各行各业的重要发展趋势。在电力行业中,智能电力运维系统是数字化转型的关键应用之一。 力安科技智能电力运维系统是一种集自动化、智能化、云计算、物联网等先进技术于一体的电力运维管理解决方…...

eslint报错:no-empty-source
问题: 提交代码时,eslint校验没有通过,报错 esc[2m183:9esc[22m esc[31mesc[31m✖esc[39m Unexpected empty source esc[2mno-empty-sourceesc[22m 1 problem (esc[31m1 erroresc[39m, esc[33m0 warnings esc[39m) 原因: …...
)
图论17(Leetcode864.获取所有钥匙的最短路径)
用二进制表示获得的钥匙,假设n钥匙个数 000000000代表没有钥匙,0000000001代表有idx为1的钥匙,0000000011代表有idx1,2的钥匙 (这方法巧妙又复杂.. 代码: class Solution {static int[][] dirs {{-1,0}…...
vue 脚手架 入门 记录
vue 脚手架 入门 记录 以管理员身份运行PowerShell执行:get-ExecutionPolicy,回复Restricted,表示状态是禁止的 3.执行:set-ExecutionPolicy RemoteSigned 4.选择Y 注意:一定要以管理员的身份运行PowerShellÿ…...

汽车租赁系统演示租车小程序H5开发
一款适合汽车租赁业务的程序系统,支持在线支付、一键续租、在线签名。 为了方便用户端方便租车和查看已租车辆的信息和费用,支持上门取车和到店取车两种模式,支持待付款、待取车、待还车、订单管理、已完成、全部订单等订单状态查看和处理功…...

【MySQL】 MySQL 更新数据机制
MySQL 更新数据机制 一、问题描述 假设我们有这样一张表,且包含一条记录: CREATE TABLE mytest ( id int(11) NOT NULL, c1 int(11) DEFAULT NULL, c2 int(11) DEFAULT NULL, c3 int(11) DEFAULT NULL, PRIMARY KEY (id), KEY c1 (c1), KEY c2 (c2) 包…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...
