蓝桥杯2023年第十四届省赛真题-异或和之和--题解
目录
蓝桥杯2023年第十四届省赛真题-异或和之和
题目描述
输入格式
输出格式
样例输入
样例输出
【代码实现】
大家觉得写得可以的话,可以加入QQ群907575059.
蓝桥杯2023年第十四届省赛真题-异或和之和
时间限制: 3s 内存限制: 320MB 提交: 241 解决: 66
题目描述
给定一个数组 Ai,分别求其每个子段的异或和,并求出它们的和。或者说,对于每组满足 1 ≤ L ≤ R ≤ n 的 L, R ,求出数组中第 L 至第 R 个元素的异或和。然后输出每组 L, R 得到的结果加起来的值。
输入格式
输入的第一行包含一个整数 n 。
第二行包含 n 个整数 Ai ,相邻整数之间使用一个空格分隔。
输出格式
输出一行包含一个整数表示答案。
样例输入
复制
5 1 2 3 4 5
样例输出
复制
39
【代码实现】
package LQB;import java.util.Scanner;/*** @ProjectName: study3* @FileName: Ex5* @author:HWJ* @Data: 2023/9/18 20:35*/
public class Ex5 {public static void main(String[] args) {Scanner input = new Scanner(System.in);int n = input.nextInt();int[] arr = new int[n];for (int i = 0; i < n; i++) {arr[i] = input.nextInt();}long res = 0;for (int i = 0; i < n; i++) {long sum = arr[i];res += sum;for (int j = i + 1; j < n; j++) {sum ^= arr[j];res += sum;}}System.out.println(res);}}
相关文章:

蓝桥杯2023年第十四届省赛真题-异或和之和--题解
目录 蓝桥杯2023年第十四届省赛真题-异或和之和 题目描述 输入格式 输出格式 样例输入 样例输出 【代码实现】 大家觉得写得可以的话,可以加入QQ群907575059. 蓝桥杯2023年第十四届省赛真题-异或和之和 时间限制: 3s 内存限制: 320MB 提交: 241 解决: 66 …...

Linux 常用命令学习笔记
Linux 常用命令学习笔记 文件操作 ls:列出当前目录下的文件和文件夹。 ls -l:以长格式显示文件和文件夹的详细信息。ls -a:显示所有文件,包括隐藏文件。 cd [目录]:切换到指定目录。pwd:显示当前工作目录…...

支撑电动汽车规模化,特来电智能化升级群充产品
9月26日,中国领先的充电网生态运营商特来电重磅发布智能群充4.0产品,标志着特来电群充产品体系进一步升级,充电行业迎来更高质量、更高性能的设备与系统,充电网基础设施将更好地支撑大规模电动汽车的发展。 群充技术路线引领充电…...

本次CTF·泰山杯网络安全的基础知识部分
简记23年九月参加的泰山杯网络安全的部分基础知识的题目,随时补充 1. 国密算法哪个属于公钥? SM2 a. 国产密码算法(国密算法)是指国家密码局认定的国产商用密码算法,目前主要使用公开的SM2、SM3、SM4三类算法&#x…...
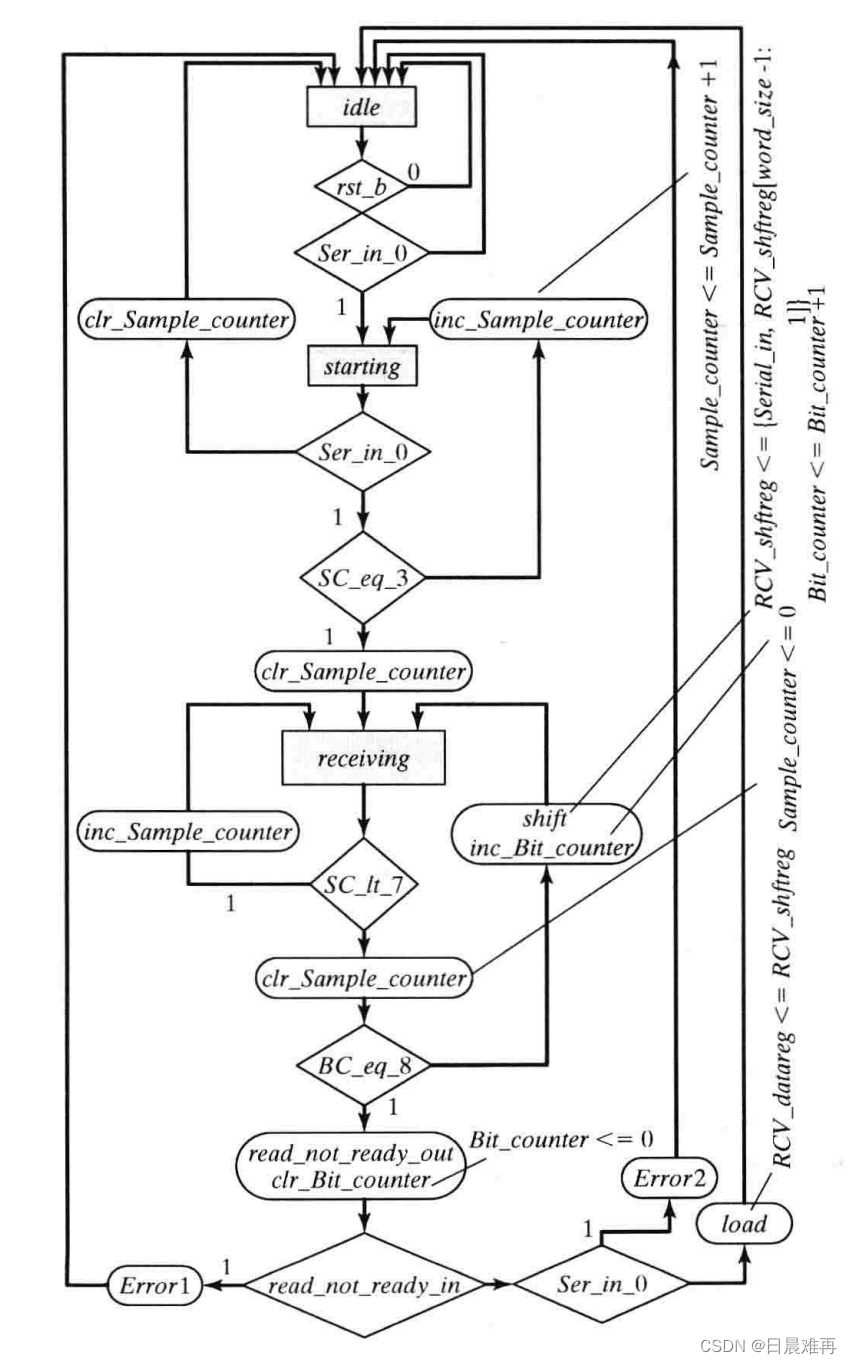
通信协议:Uart的Verilog实现(下)
4、UART接收器 UART接收器负责接收串行比特流,去除起始位和停止位,并以并行格式将数据保存到与主机数据总线相连的寄存器里。接收器无法获得发送时钟,因此尽管数据以标准比特率到达,但数据未必与接收主机内的时钟同步。同步问题可…...
嵌入式MCU都有什么高级用法?
嵌入式MCU都有什么高级用法? 您举的几个例子,确实是MCU外设的一些高端玩法。只是不知道您是否想过,既然这些机制是被 人设计出来的,那它就是种标准用法。从微控制器的发展历程来看,许多硬件机制都是有了实际 需求后才…...

热启动和冷启动是什么,区别
app冷启动: 当应用启动时,后台没有该应用的进程,这时系统会重新创建一个新的进程分配给该应用, 这个启动方式就叫做冷启动(后台不存在该应用进程)。冷启动因为系统会重新创建一个新的进程分配给它ÿ…...
(灵神笔记))
每日一题 494目标和(0-1背包)(灵神笔记)
0-1背包模版 有n个物品,它们有各自的体积和价值,现有给定容量的背包,如何让背包里装入的物品具有最大的价值总和? 当前操作?枚举第i个物品选还是不选,不选容量不变,选容量减少 子问题ÿ…...

软件测试工作步骤详情
软件测试步骤按照研发阶段一般分为5个部分:单元测试、集成测试、确认测试、系统测试、验收测试,下面将不同阶段需要的一些工作内容做一下梳理希望可以帮助到大家。 一、单元测试的内容:(白盒为主,黑盒为辅)…...

java项目之列车票务信息管理系统(ssm源码+文档)
项目简介 列车票务信息管理系统实现了以下功能: 管理员:个人中心、用户管理、车票信息管理、购票指南管理、管理员管理、论坛管理、我的收藏管理、系统管理、订单管理。前台首页:首页、车票信息、购票指南、我的收藏管理、论坛信息、我的、…...

【Pytorch笔记】3.数学运算
深度之眼官方账号 - 01-03-mp4-张量操作与线性回归 torch.add() 功能:逐元素计算inputalphaother。 torch.add(input,alpha1,other,outNone)input:tensor; alpha:other的系数,是个实数; other࿱…...
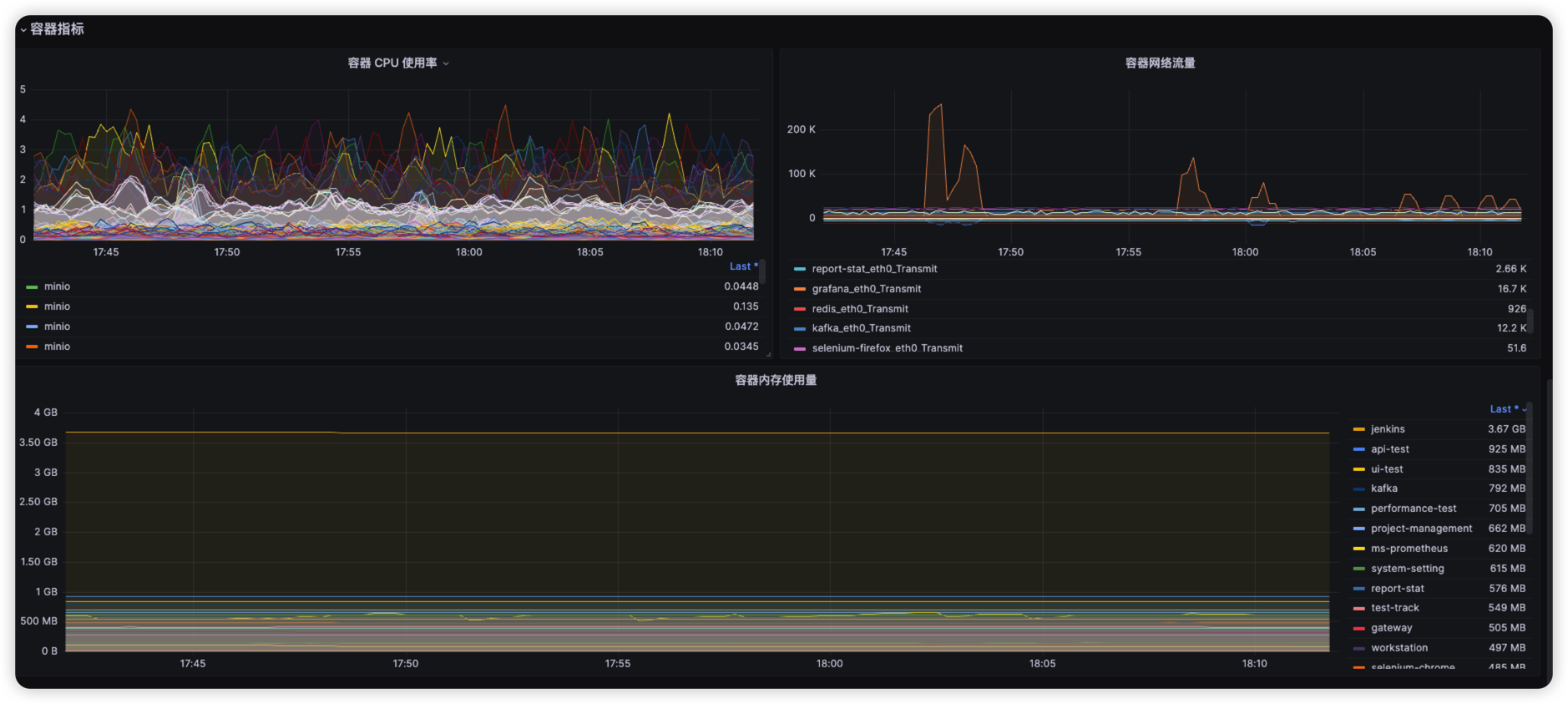
MeterSphere 监控方案
前言:在部署MeterSphere之后,很多时候需要看下MeterSphere服务的监控信息,虽然有监控告警脚本,但还不是太直观,所以就结合 PrometheusExporterGrafana 部署一套完整的MeterSphere监控方案。 首先我们先罗列一下需要监控…...
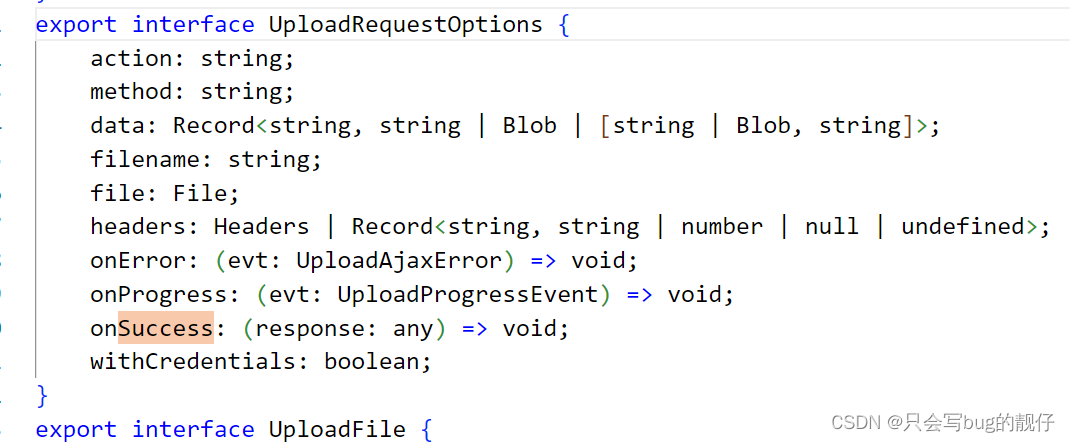
elementui-plus+ts+axios使用el-upload组件自定义上传
1.前言: 使用element ui有很多便捷之处,但是由于是封装的组件和自己写还是有些许的不一样,这里主要解决几个问题。 1. 如何获取子组件实例 2. 如何自定义上传方法 2.两个问题: ⛺️ 获取子组件实例 实际上vue一般通过ref获取子组…...

【STM32单片机】u8g2智能风扇设计
文章目录 一、功能简介二、软件设计三、实验现象联系作者 一、功能简介 本项目使用STM32F103C8T6单片机控制器,使用按键、IIC OLED模块、DS18B20温度传感器、直流电机、红外遥控等。 主要功能: 初始化后进入温度显示界面,系统初始状态为手动…...
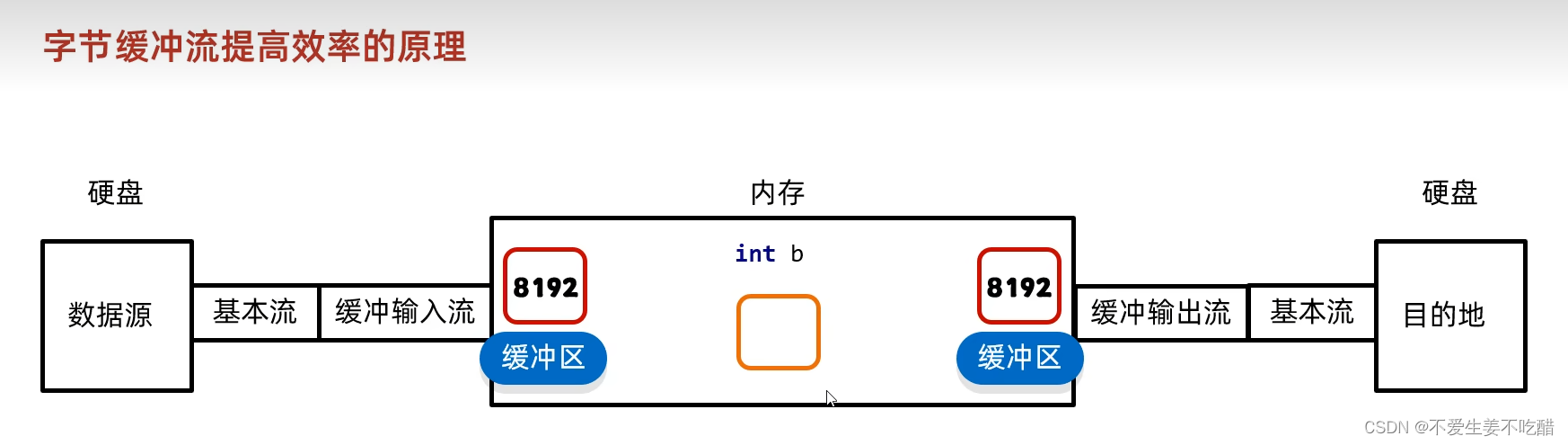
Java中的IO流的缓冲流
不爱生姜不吃醋⭐️ 如果本文有什么错误的话欢迎在评论区中指正 与其明天开始,不如现在行动! 文章目录 🌴IO流体系结构🌴缓冲流1.提高效率的原理2.缓冲流的类型3.字符缓冲流两个特有方法 🌴总结 🌴IO流体系…...
7、SpringBoot_高级配置
一、配置高级 1.临时属性设置 1.1引出问题 如果目标电脑上8080端口已经使用,再次使用该端口会出现端口占用问题 解决方式 重新更换配置文件修改端口打包通过临时属性配置新端口更换配置文件 1.2添加临时属性配置 通过临时属性修改8080端口 java -jar 项目.jar…...
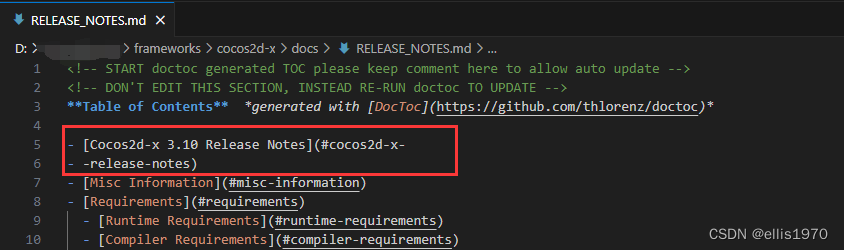
cocos2dx查看版本号的方法
打开文件:项目根目录\frameworks\cocos2d-x\docs\RELEASE_NOTES.md 知道引擎版本号的意义: 1.面试中经常被问到(面试官想知道你会不会查版本号,你会查也不一定会去看,如果你去看了说明你是一个有心人,或者想深入研究下…...
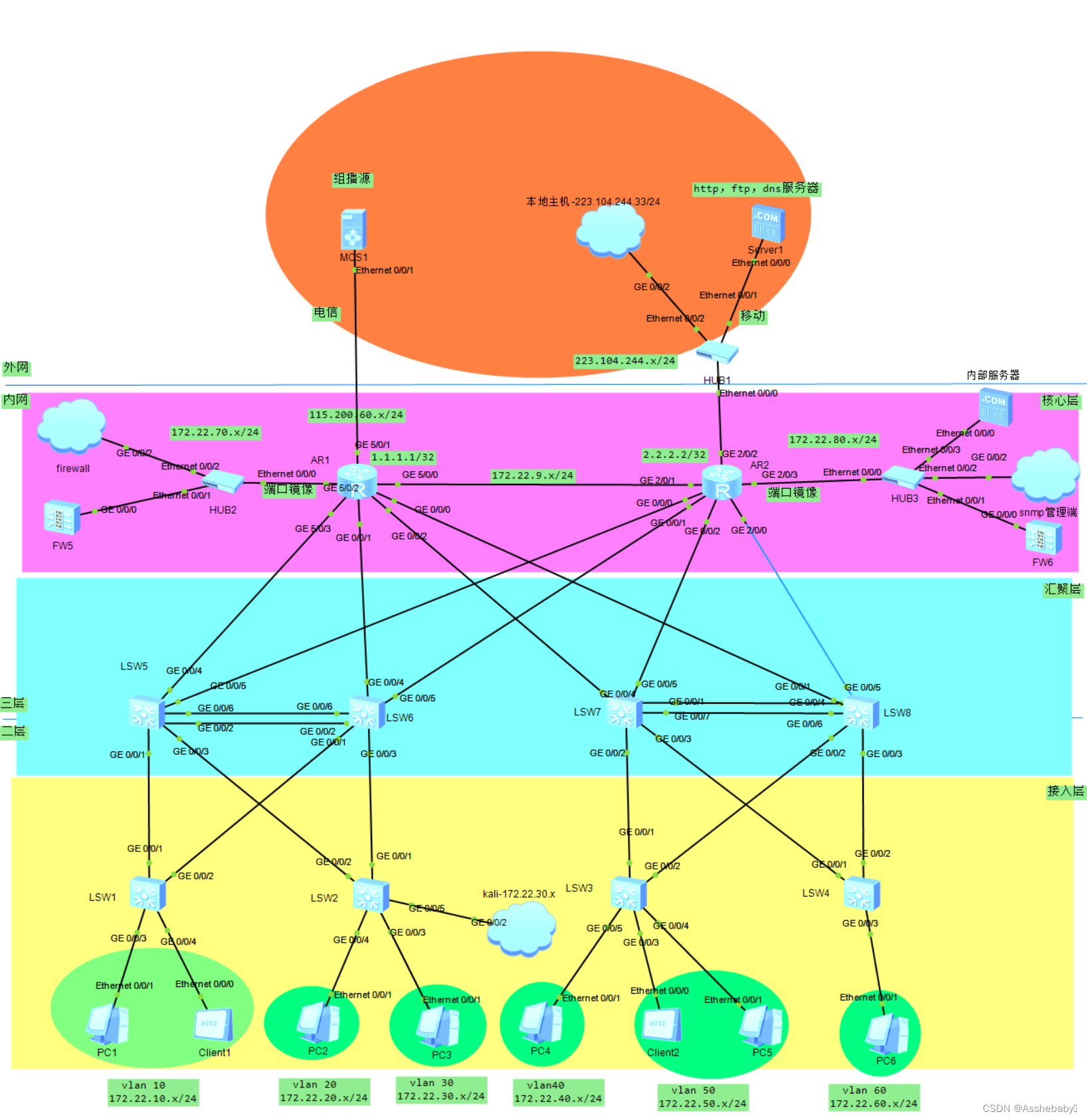
某高校的毕设
最近通过某个平台接的单子,最后Kali做的测试没有公开可以私聊给教程。 下面是规划与配置 1.vlan方面:推荐一个vlan下的所有主机为一个子网网段 连接电脑和http客户端的接口配置为access接口 交换机与交换机或路由器连接的接口配置为trunk接口---也可以…...

利用uvicorn、Starlette和pipeline将一个训练好的大模型发布成一个web服务
技术名词: 1、Starlette: 它是一个轻量级、高度可用性和可扩展性的Web框架,它专门为异步应用程序设计。 Starlette基于Python 3.6的异步/协程语法,具有快速响应性能和低延迟。你可以将它理解为Java的Spring。 安装:…...

贝赛尔曲线 - Vue3实现加入购物车抛物线效果组件
贝赛尔曲线 - Vue3实现加入购物车抛物线效果组件(可连续多个动画,动态回收DOM) 前言 在前几天的一次迭代中,我遇到了这么一个需求,模仿支付宝首页应用中心的编辑功能,支持编辑首页展示的应用,…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...

跨平台商品数据接口的标准化与规范化发展路径:淘宝京东拼多多的最新实践
在电商行业蓬勃发展的当下,多平台运营已成为众多商家的必然选择。然而,不同电商平台在商品数据接口方面存在差异,导致商家在跨平台运营时面临诸多挑战,如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...

高效的后台管理系统——可进行二次开发
随着互联网技术的迅猛发展,企业的数字化管理变得愈加重要。后台管理系统作为数据存储与业务管理的核心,成为了现代企业不可或缺的一部分。今天我们要介绍的是一款名为 若依后台管理框架 的系统,它不仅支持跨平台应用,还能提供丰富…...
