多边形碰撞检测算法
1、AABB碰撞检测算法
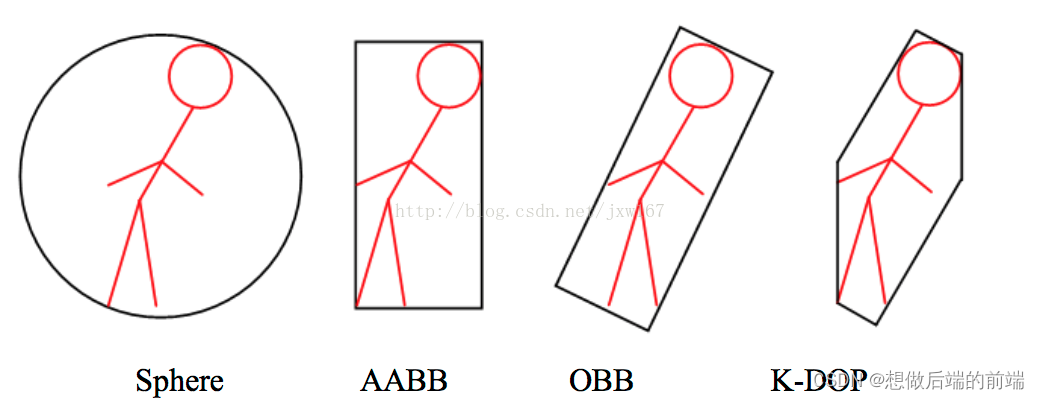
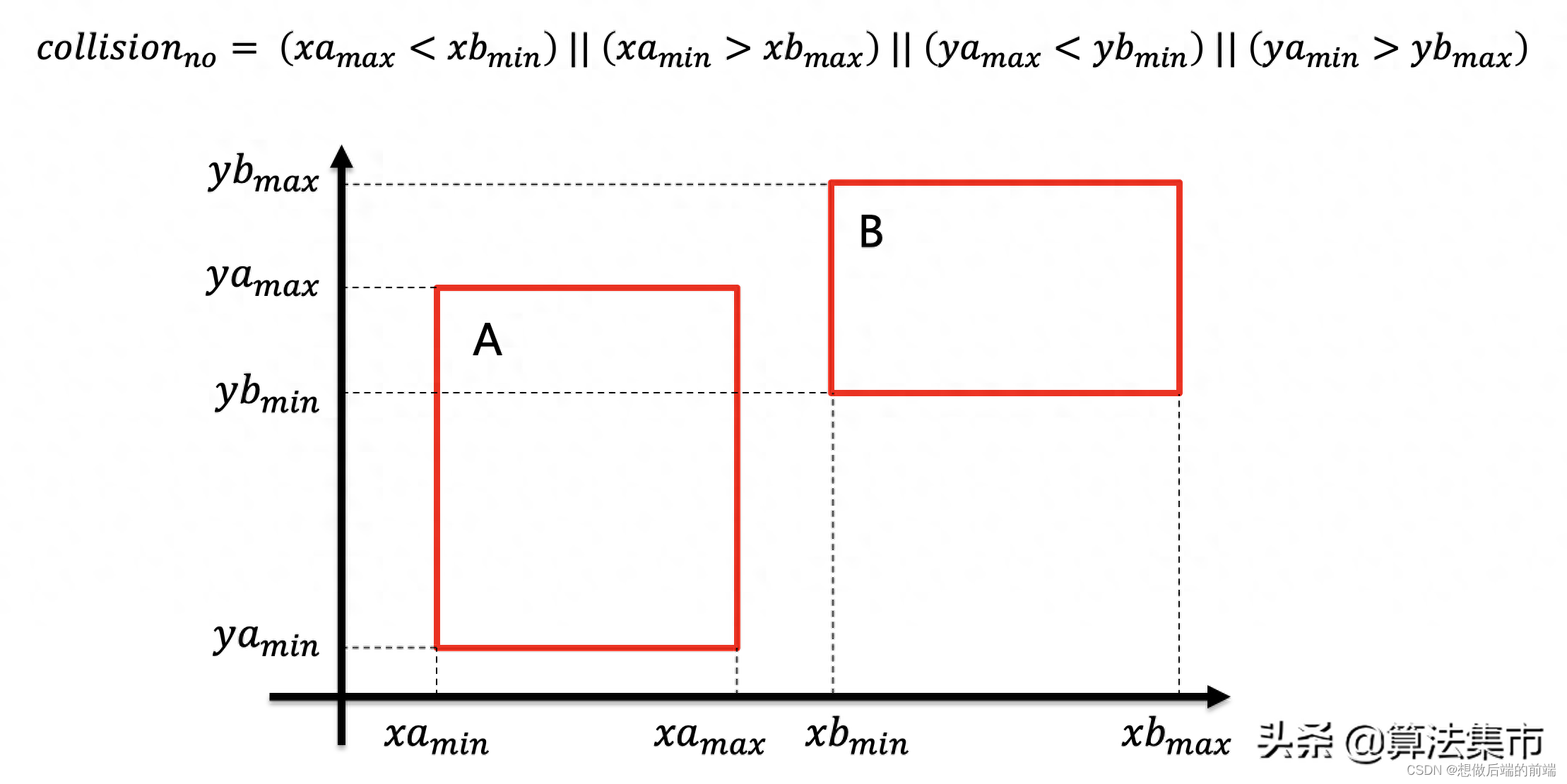
AABB碰撞检测指轴对齐碰撞箱(Axis-aligned Bounding Box),是分别从x轴向和y轴向进行碰撞检测的算法。即对于需要检测的物体A和物体B我们需要将其用A盒和B盒套起来,判断A盒和B盒在x轴向和y轴向是否发生碰撞,只有在x轴向和y轴向都发生碰撞我们才判断它发生了碰撞。
在轴对齐包围矩形(Axis Aligned Bounding Box,AABB)基础之上,更为准确的是 转向包围矩形(Oriented Bounding Box,OBB) OBB 与 AABB 的差别在于物体旋转之后,AABB的大小会发生改变,保证每条边与某个坐标轴平行;OBB 的大小则不会改变,且将随物体一起旋转。
2、OBB碰撞检测算法
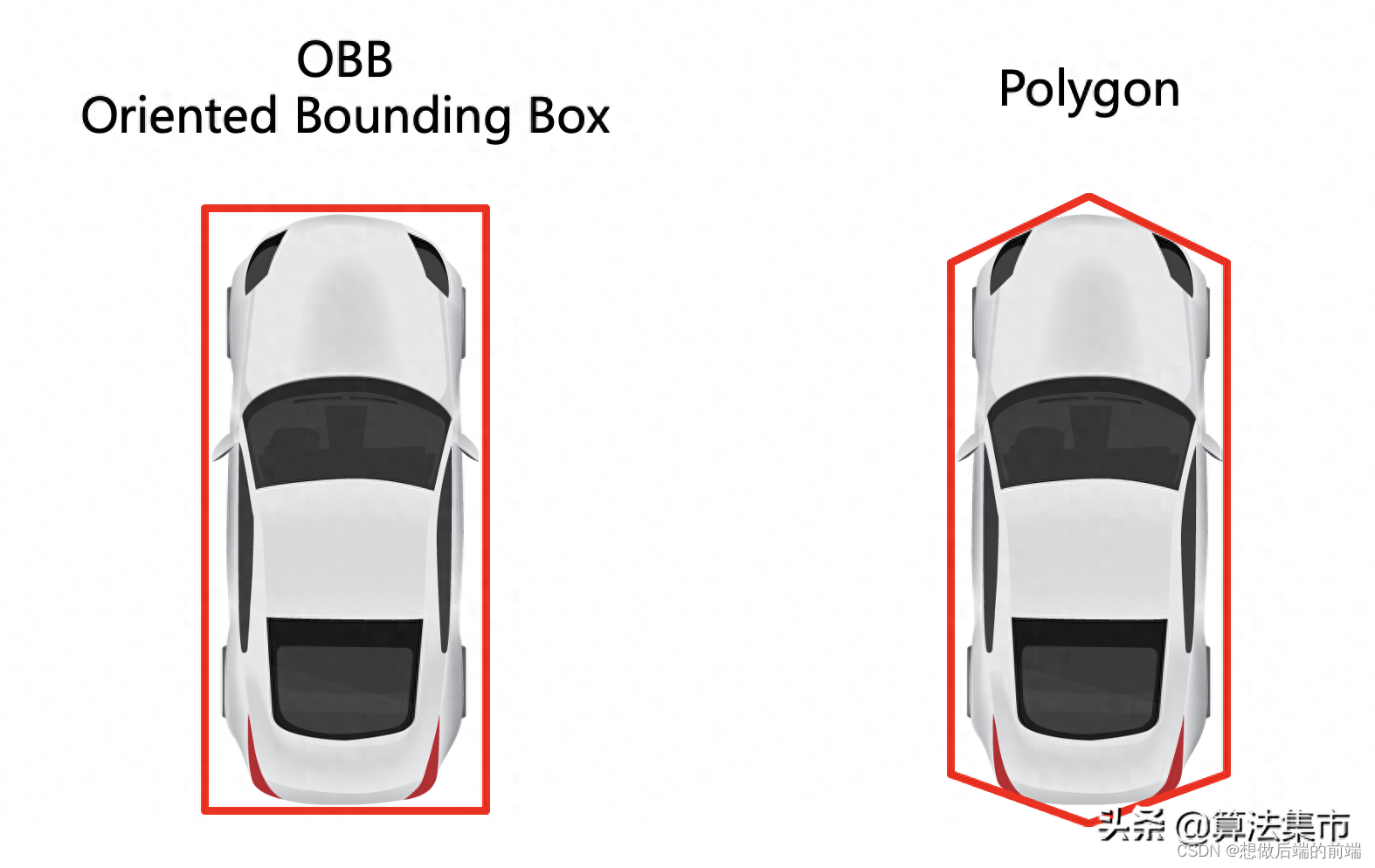
OBB 就是找一个最小的包围物体的矩形,这在自动驾驶系统中也是最常用的,感知模块给出物体的轮廓通常就是此形状。另外,为了准确描述物体轮廓,感知模块在 bounding box 的基础上,通常还会给出 polygon(多边形)的形式,如下图所示。
相对于AABB包围盒来讲,OBB在碰撞精度上要高于AABB,但是精确度的提高同时带来的就是效率的降低,OBB的算法无疑是要比AABB复杂的,同样内存消耗也会更大。
在了解OBB算法之前我们需要先学习一下分离轴定理。
分离轴定理(SAT):
分离轴定理(Separating Axis Theorem)的理论依据为超平面分离定理,即 令 A 和 B 是两个不相交的非空凸集,那么存在一个非零向量 v 和 实数 c,使得 <x, v> ≤ c 且 <y, v> ≥ c。其中,x 属于 A,y 属于 B。
简单来说,就是对于两个凸多边形,若存在一条直线将两者分开,则这两个多边形不相交。
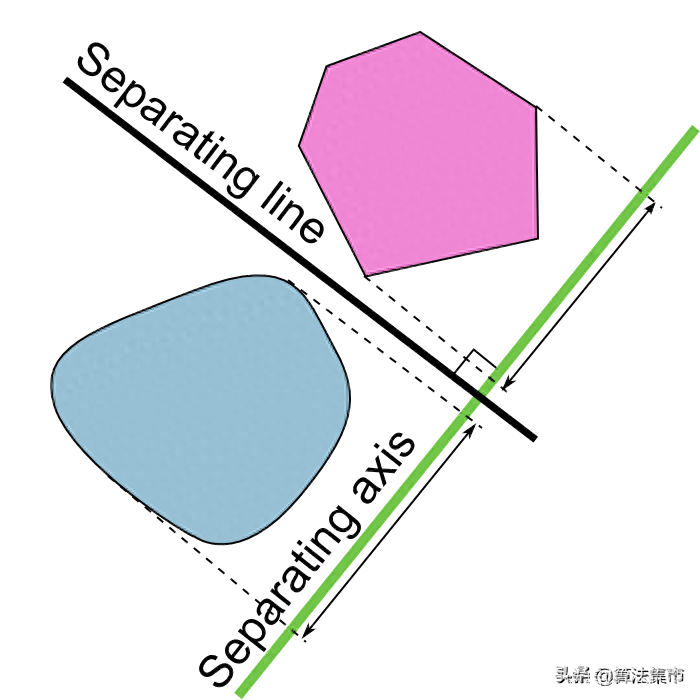
上图中的黑线为分离线(Seperating line),与之垂直的绿线为分离轴(Separating axis),图中虚线表示的是多边形在分离轴上的投影。
实际应用中,遍历所有角度的分离轴是不现实的,受益于多边形的性质,对于两个都是多边形的物体,只需要依次在每条边的垂直线做投影即可,如下图所示。
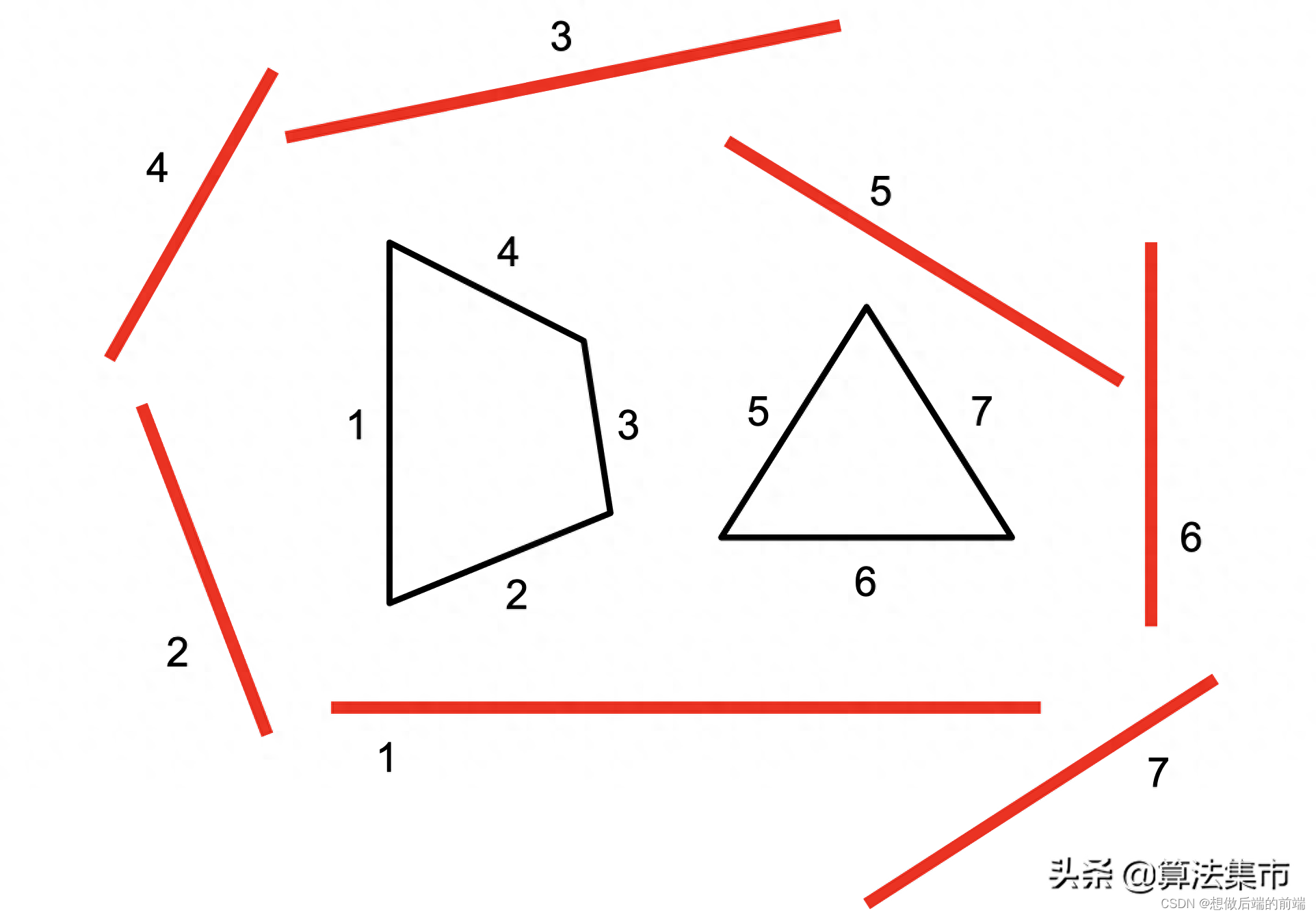
对于两个都是矩形的物体,则更简单,只需要做四次投影。
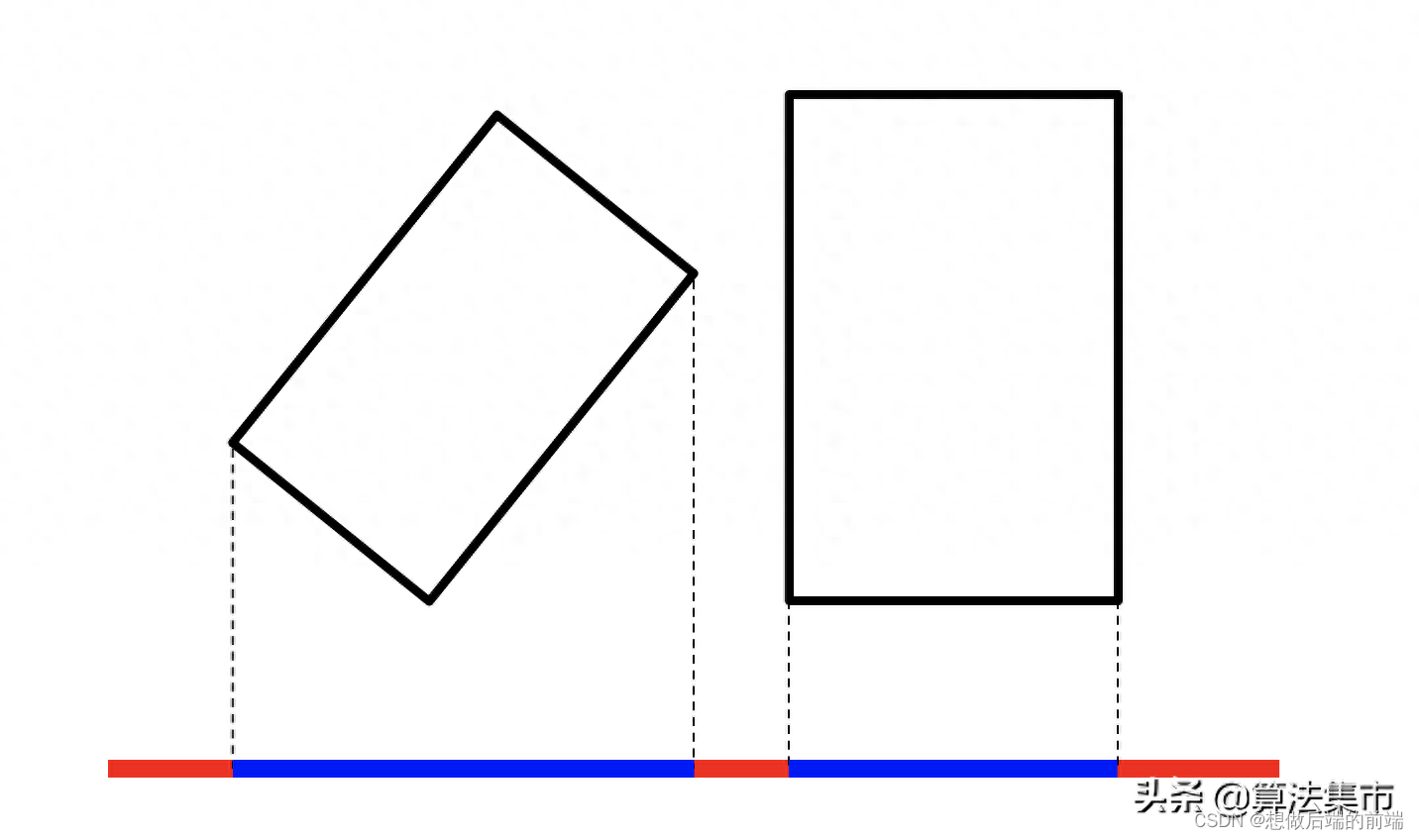
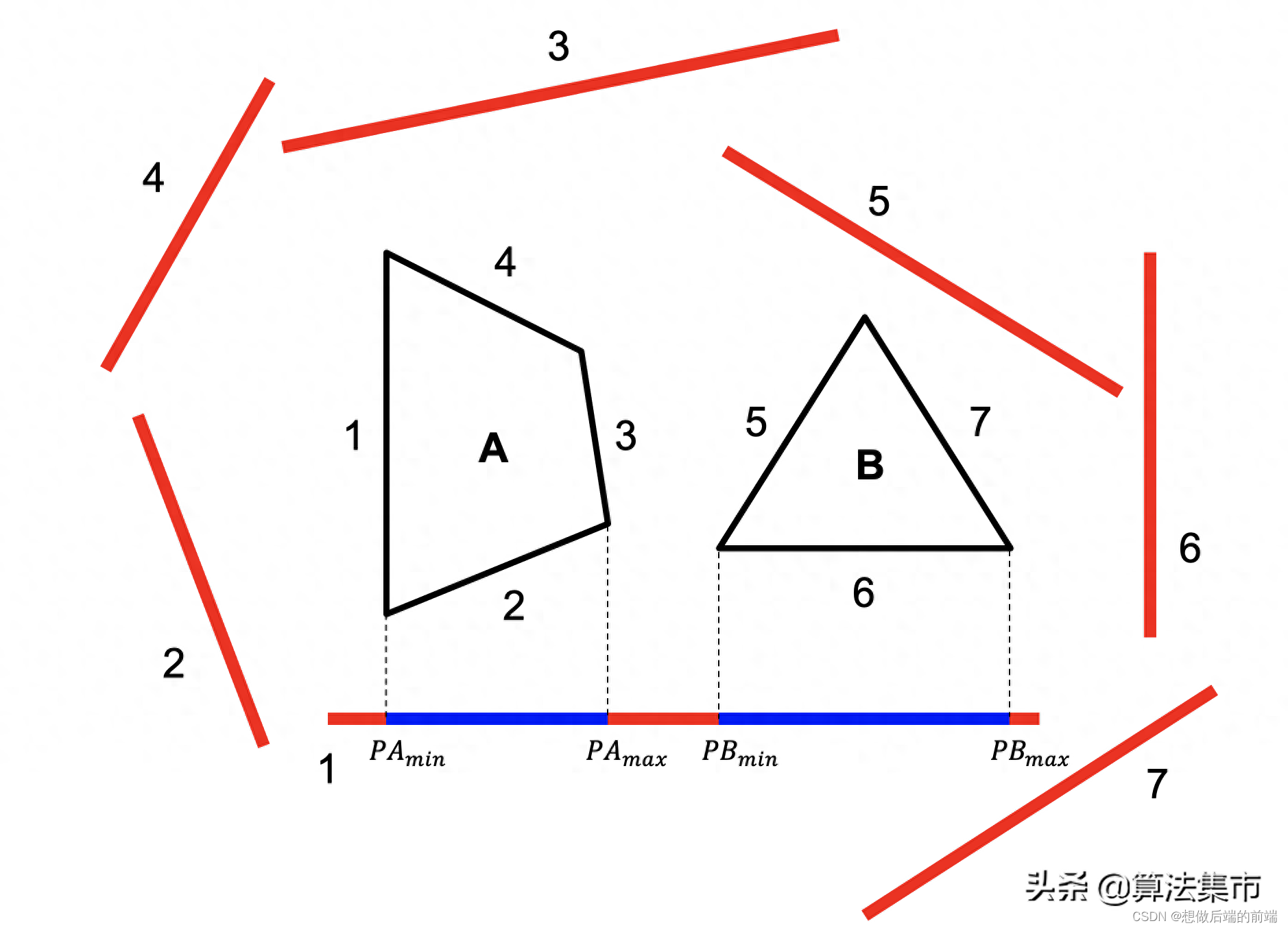
以下图中的两个多边形 A 和 B 为例,分离轴定理的具体步骤为:
- 首先根据边1的两个顶点位置坐标,计算出边1的向量,设为(x,y);
- 进而求出边1的法向量,作为分离轴,为(y, -x)或(-y,x)。若需要求两个多边形的最小分离距离,这里的法向量还需要化为单位向量;若只需判断两个多边形是否相交,则不需要化为单位向量;
- 依次将多边形 A 和 B的所有顶点与原点组成的向量投影到这个分离轴上,并记录两个多边形顶点投影到分离轴上的最小值和最大值(Pmin,Pmax),形成一个投影线段;
- 判断这两个投影线段是否发生重叠,若不重叠,则有 (PAmax < PBmin)||(PAmin > PBmax);
- 若两个投影线段不重叠,则代表存在这样一条直线将两个多边形分开,两个多边形不相交,可以直接退出循环;
- 若两个投影线段重叠,则回到步骤1,继续以边2的法向量作为分离轴,进行投影计算;
- 当两个多边形的所有边都检查完之后,找不到这样一条分离的直线,则意味着两个多边形相交。
注意:分离轴定理是一种适用于凸多边形的碰撞检测算法,对于凹多边形则不适用,如下图所示,两个多边形没有碰撞,但找不到这样一条直线,能将两者分开。所以如果是凹多边形的话,需要先将其转换成多个凸多边形。

综上,分离轴定理是一种适用于 bounding box 和 polygon 的精细碰撞检测算法,其优点是算法原理简单,可准确判断两个多边形是否相交;缺点在于当多边形的边数较多时,该算法的效率较低(当两个多边形相交时,需要遍历完所有边进行判断)。
在实际应用中,为了提高效率,通常先使用 基于轴对齐包围矩形(AABB)的方法进行粗略的碰撞检测,然后再使用分离轴定理(SAT)做精细碰撞检测。
3、GJK(Gilbert–Johnson–Keerthi)算法
GJK是由Gilbert,Johnson,Keerthi 三位前辈发明的,用来计算两个凸多面体之间的碰撞检测,以及最近距离。GJK算法可以在O(M+N)的时间复杂度内,检测出碰撞,算法在每次迭代的过程中,都会优先选择靠近原点的方向,因此收敛速度会很快。算法的证明过程比较复杂,但是原理还是比较容易理解的。
相比 SAT 算法,GJK 算法更加高效。 GJK算法的核心就是闵可夫斯基差,即若两个多边形相交,则它们的闵可夫斯基差必然包括原点。
闵可夫斯基差,也可以叫做闵可夫斯基和,它的定义也很好理解,点集A与B的闵可夫斯基和被定义为:
A + B = {a + b |a∈A,b∈B}
如果 A 和 B 是两个凸多边形,则 A + B 也是凸多边形。
闵可夫斯基和从几何上的直观理解是A集合沿B的边际连续运动一周扫过的区域与B集合本身的并集,也可以是B沿着A的边界连续运动扫过区域与A自身的并集。
GJK算法用到的不是闵可夫斯基和,而是闵可夫斯基差,即:
A – B = {a – b |a∈A,b∈B}
虽然使用的是减法运算,但其仍然是闵可夫斯基和,相当于先对B中的所有点做负运算(相对原点的镜像),然后再与A做加法。
先来看两个例子。
对于两个不相交的多边形,shape1为矩形,shape2为三角形,如下图所示。
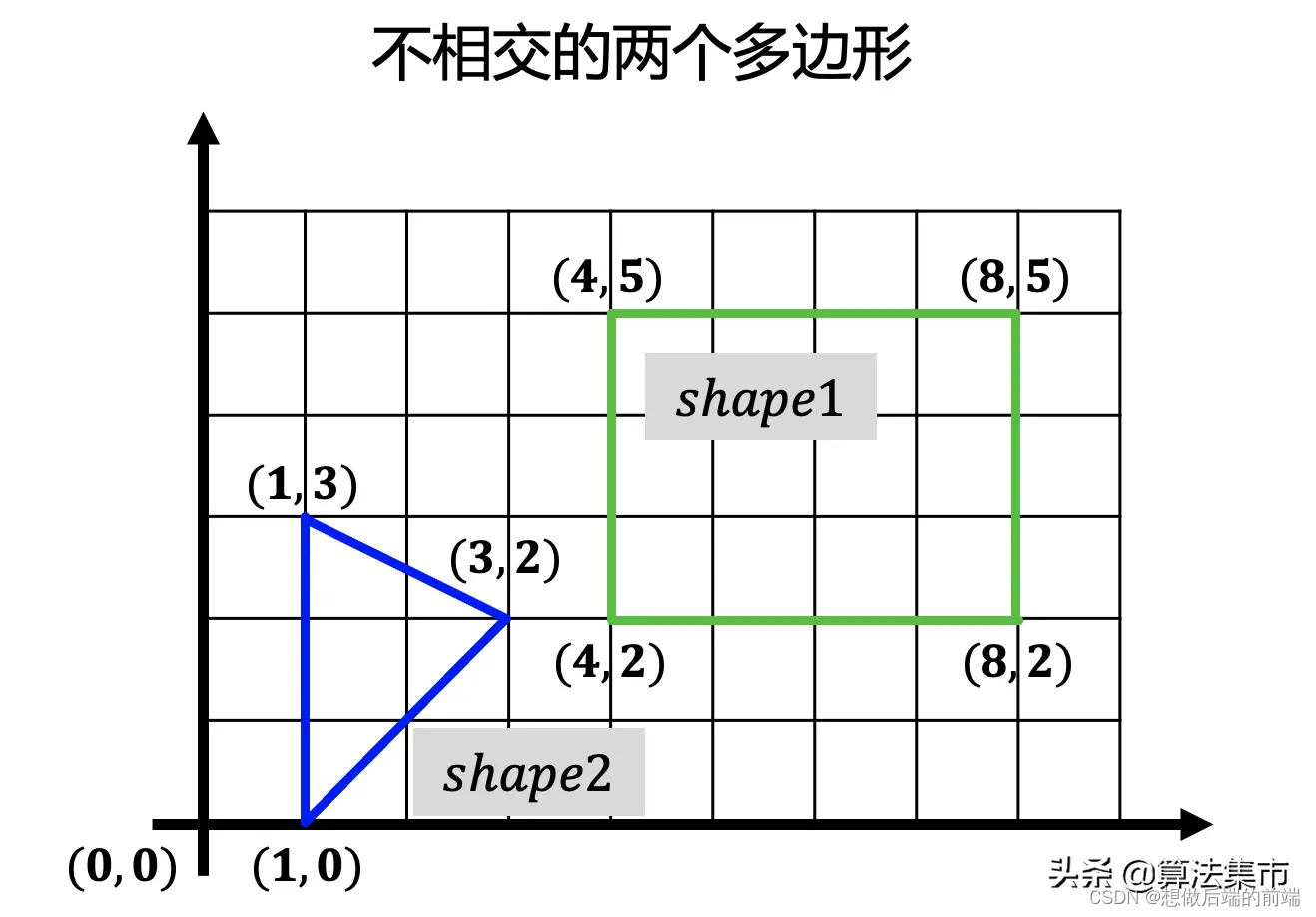
它们的闵可夫斯基差如下图所示,其闵可夫斯基差不包括原点,且两个多边形之间的距离就是其闵可夫斯基差到原点的距离。事实上,GJK 算法发明出来的初衷就是为了计算两个凸多边形之间的距离。
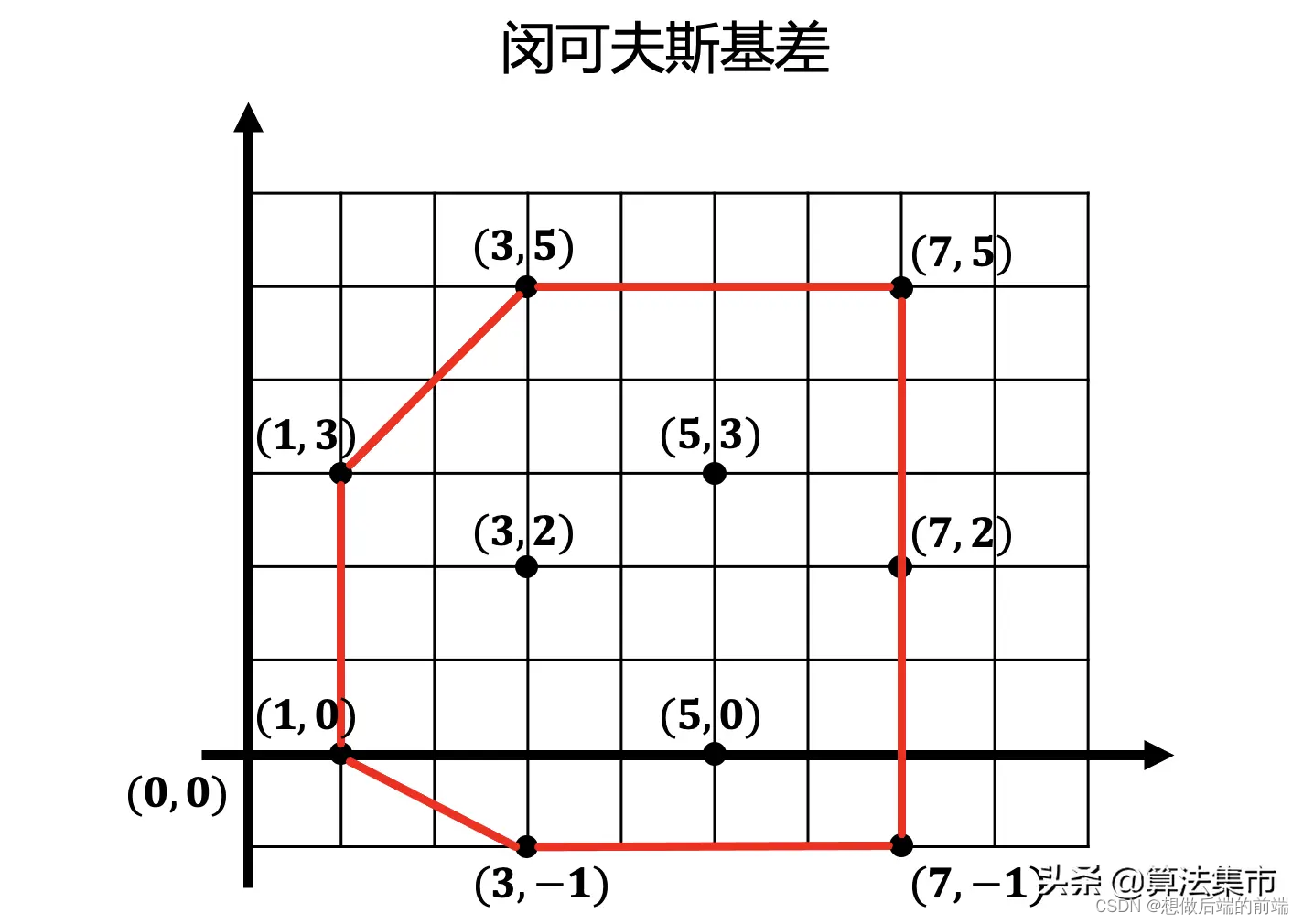
对于两个相交的多边形,shape1为矩形,shape2为三角形,如下图所示。
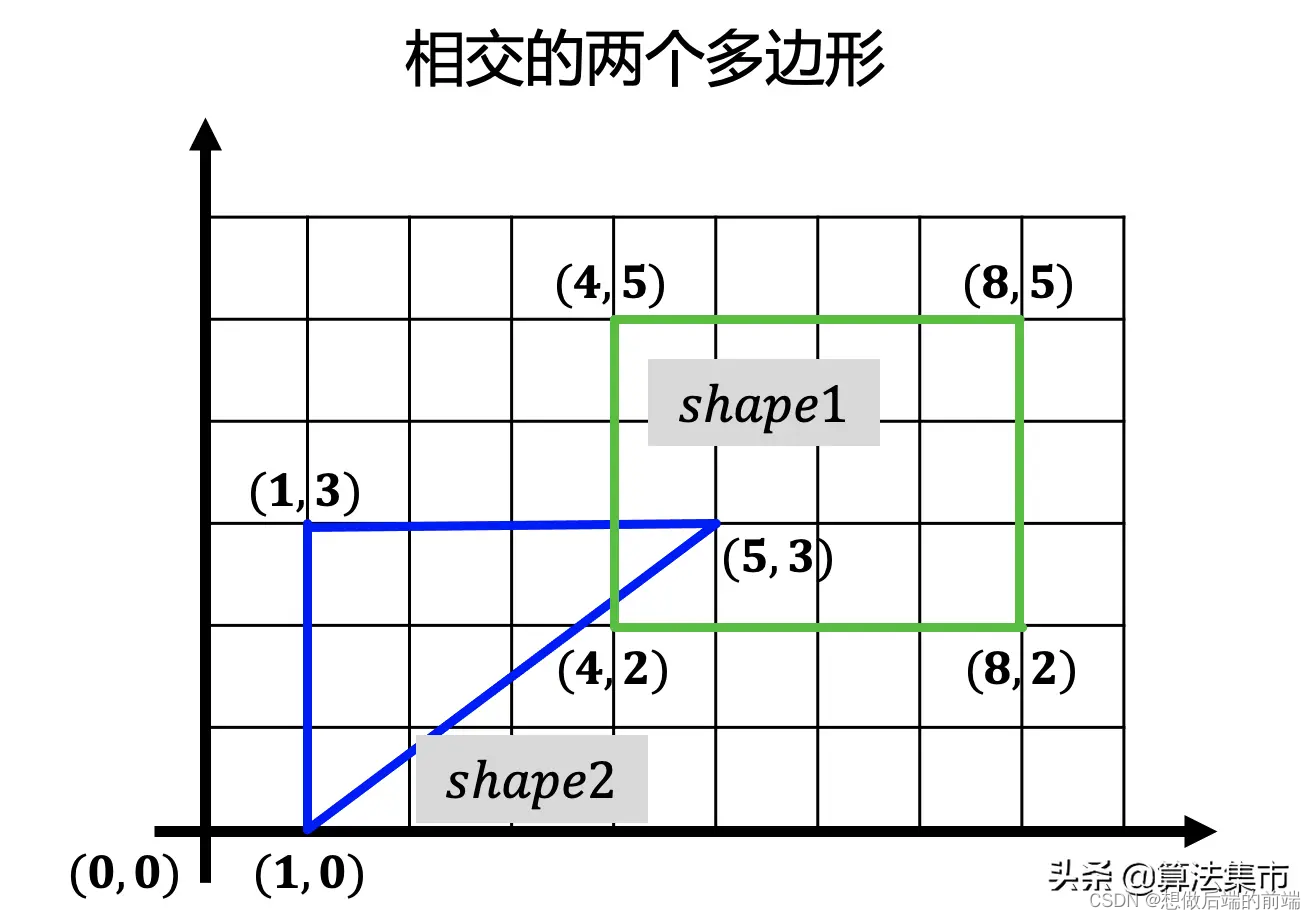
它们的闵可夫斯基差则如下图所示,可以看到,闵可夫斯基差是包括原点的。这也很好理解,两个相交的多边形,必然有一点既属于shape1,也属于shape2,相减则为原点(0,0)。
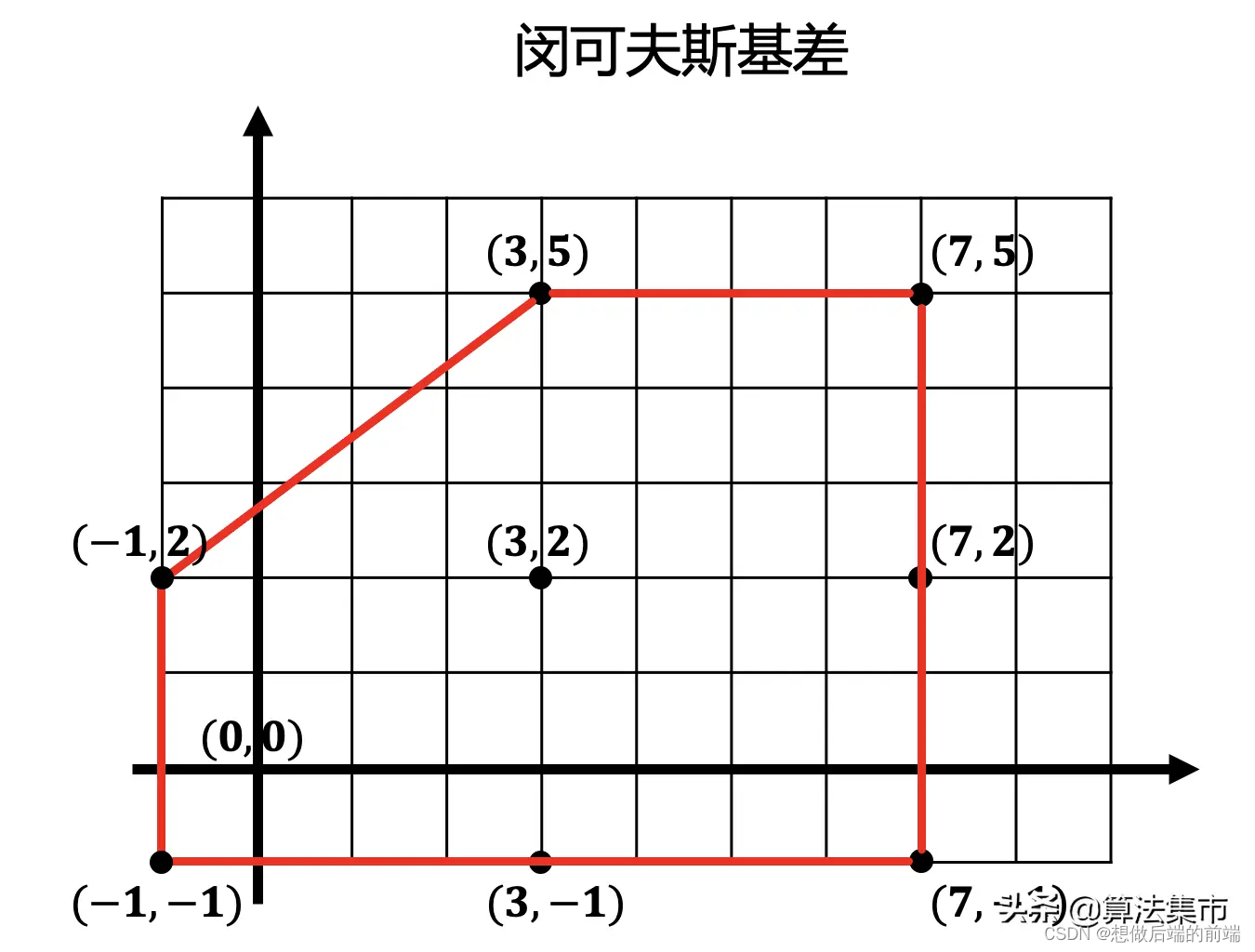
3.1 单纯形
k阶单纯形(simplex),指的是k维空间中的多胞形,该多胞形是k+1个顶点组成的凸包。
在GJK算法中,单纯形被大量使用。单纯形指的是点、线段、三角形或四面体。例如,0阶单纯形是点,1阶单纯形是线段,2阶单纯形是三角形,3阶单纯形是四面体。
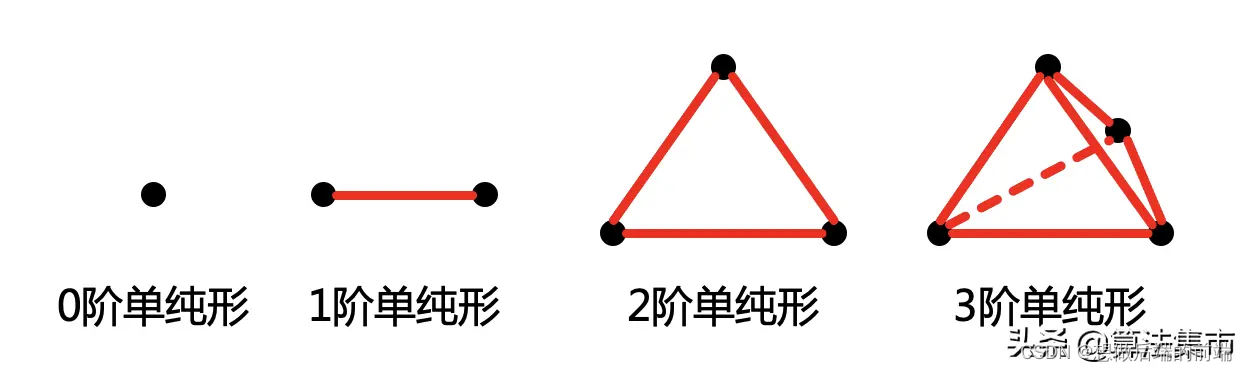
对于2维空间的多边形,最多用到2阶单纯形。那单纯形到底有什么作用呢?
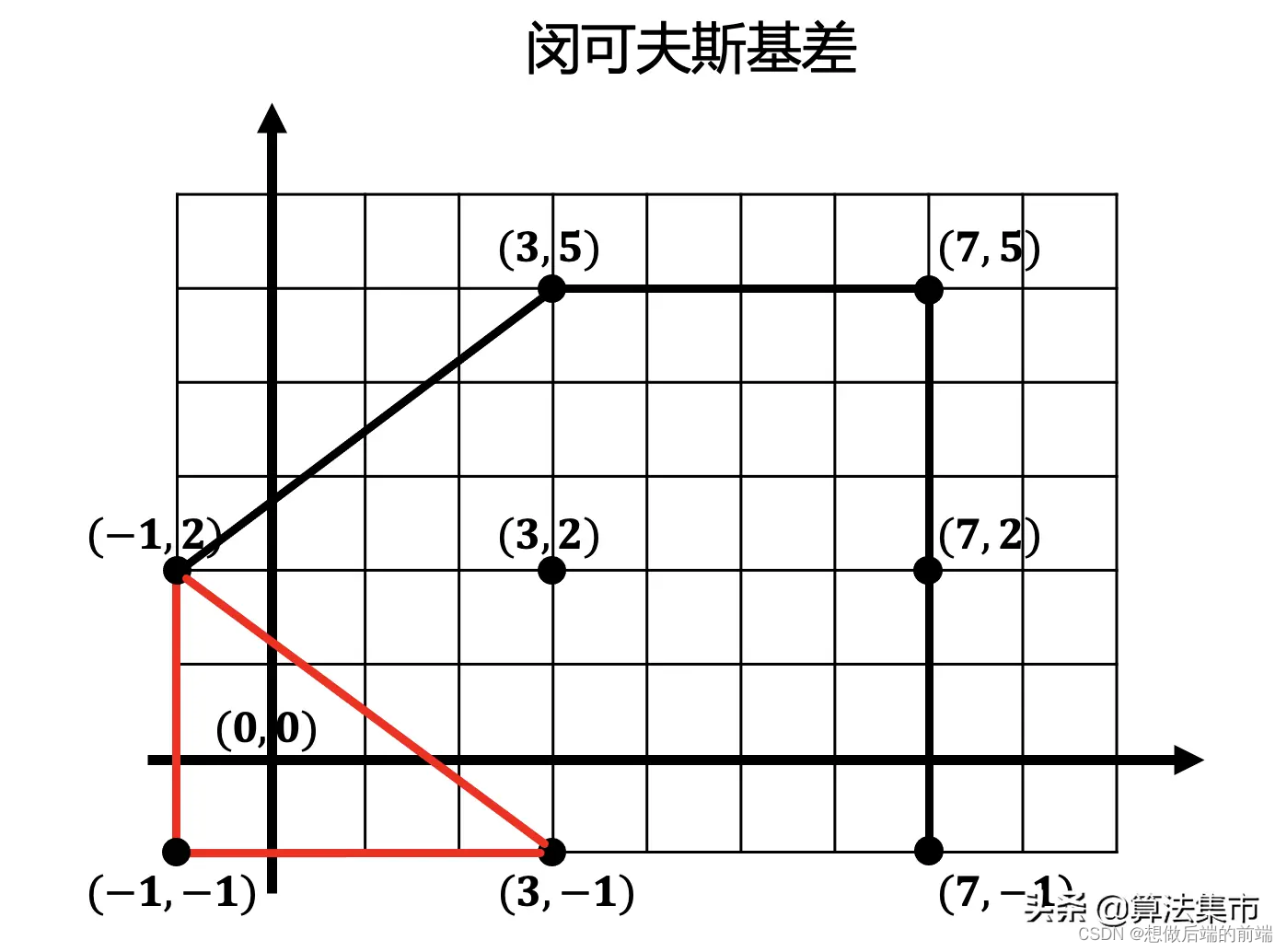
对于上面两个相交的多边形例子,实际应用中,其实不需要求出完整的闵可夫斯基差,只需要在闵可夫斯基差内形成一个多边形,如下图所示,并使这个多边形尽可能包围原点,这个多边形就称为单纯形。即假如单纯形包围原点,则闵可夫斯基差必然包围原点。
3.2 Support 函数
Support函数的作用是计算多边形在给定方向上的最远点。如下图所示,在向量 a 方向的最远点为 A 点,在向量 b 方向的最远点为 B 点。这里在寻找给定方向上的最远点时,需要用到向量的点乘。
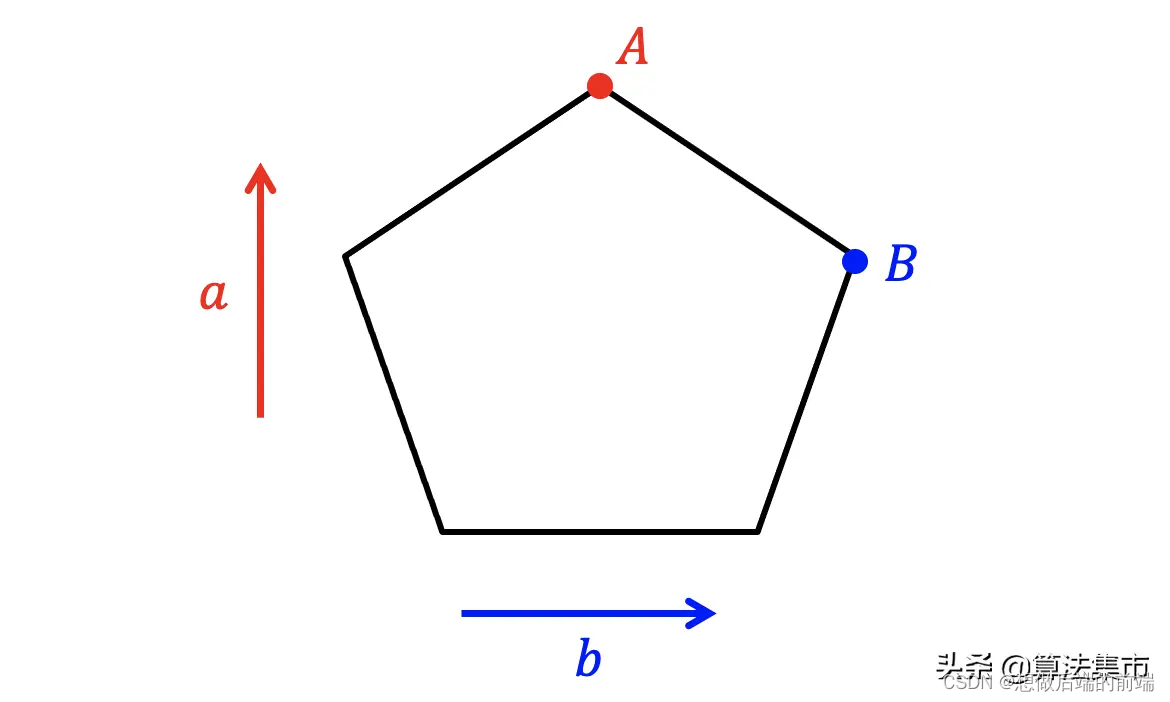
为什么需要Support函数呢?这是因为在构建单纯形时,我们希望尽可能得到闵可夫斯基差的顶点,而不是其内部的一个点,这样产生的单纯形才能包含最大的区域,增加算法的快速收敛性。
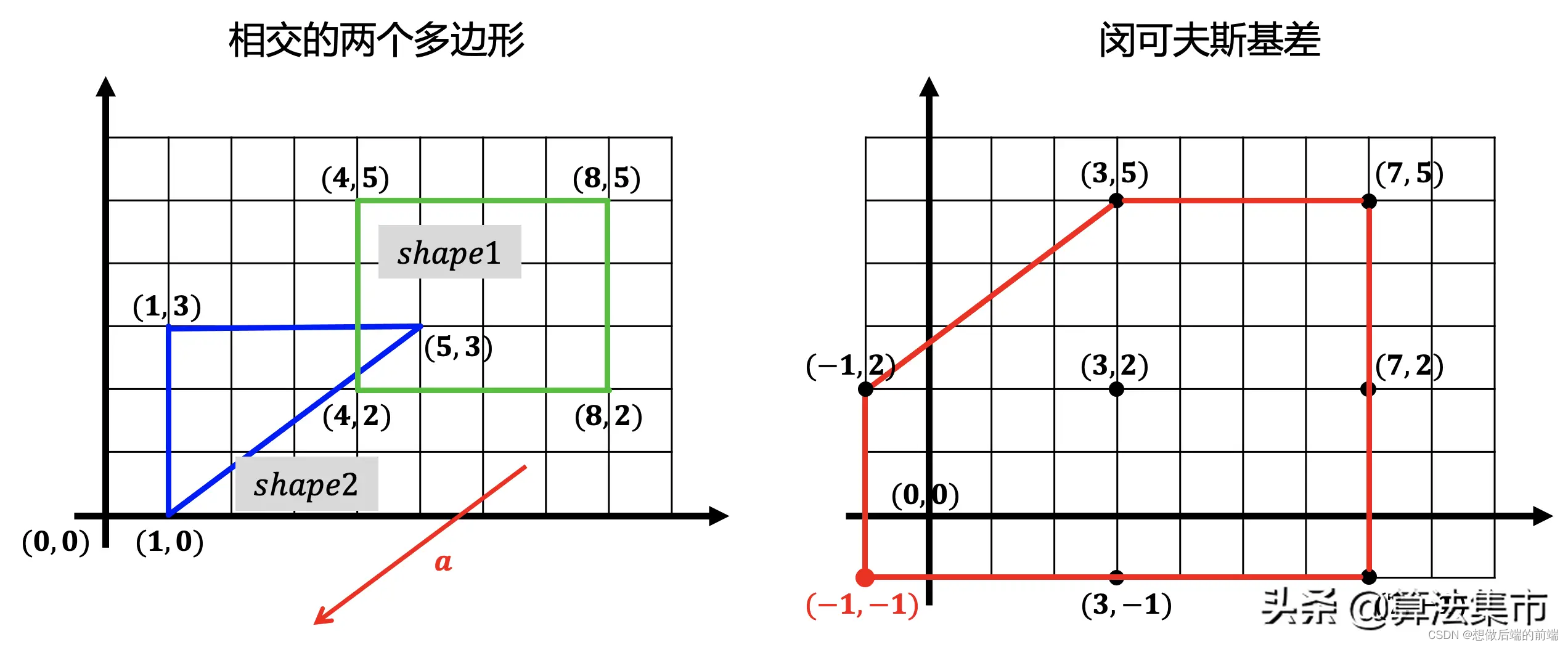
如下图所示,在给定向量 a 方向上,shape1 的最远点为(4,2),在向量 -a 的方向上,shape2 的最远点为(5,3),这两个点作差即得到点(-1,-1)。利用这种方式得到的点都在闵可夫斯基差的边上。
相关文章:

多边形碰撞检测算法
1、AABB碰撞检测算法 AABB碰撞检测指轴对齐碰撞箱(Axis-aligned Bounding Box),是分别从x轴向和y轴向进行碰撞检测的算法。即对于需要检测的物体A和物体B我们需要将其用A盒和B盒套起来,判断A盒和B盒在x轴向和y轴向是否发生碰撞,只有在x轴向和…...
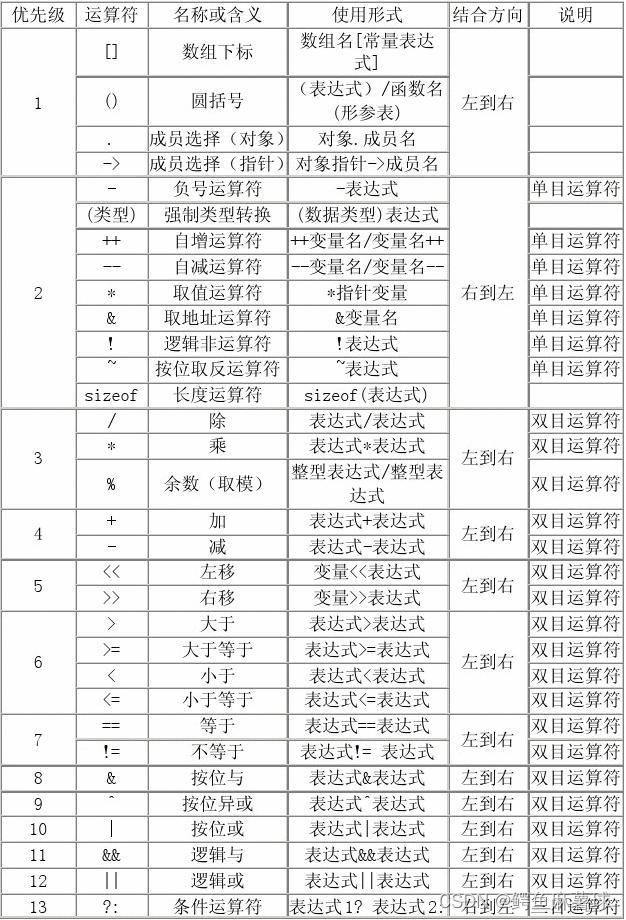
【C/C++笔试练习】——printf在使用%的注意事项、for循环语句的三个条件、运算符优先级、删除公共字符
文章目录 C/C笔试练习1.%符号在printf用作格式说明符的注意事项(1)输出%5.3s(2)判断%中小数点含义 2.for循环语句的三个条件(3)判断循环次数(4)判断循环次数 3.运算符优先级…...
Linux部署elk日志监控系统
目录 一、简介 二、部署elasticsearch 2.1 安装jdk11(jdk版本>11) 2.2 下载安装包 2.3 授权elk用户 2.4 配置elasticsearch.yml 2.5 启动elasticsearch 三、部署logstash 3.1 启动测试 3.2 可能出现的报错 3.3 指定配置文件启动logstash 3.4 安装El…...
)
LINUX -SQL笔记(自学用)
1.安装 sudo apt-get install mysql-server sudo mysql -u root -p2.关系模型 在关系数据库中,一张表中的每一行数据被称为一条记录。一条记录就是由多个字段组成的。 每一条记录都包含若干定义好的字段。同一个表的所有记录都有相同的字段定义。 对于关系表&#…...
【Spark】win10配置IDEA、saprk、hadoop和scala
终于,要对并行计算下手了哈哈哈。 一直讲大数据大数据,我单次数据处理量大概在1t上下,是过亿级的轨迹数据。 用python调用multiprogress编写的代码,用多线程也要一个多月跑完。 我对这个效率不太满意,希望能快一点再快…...
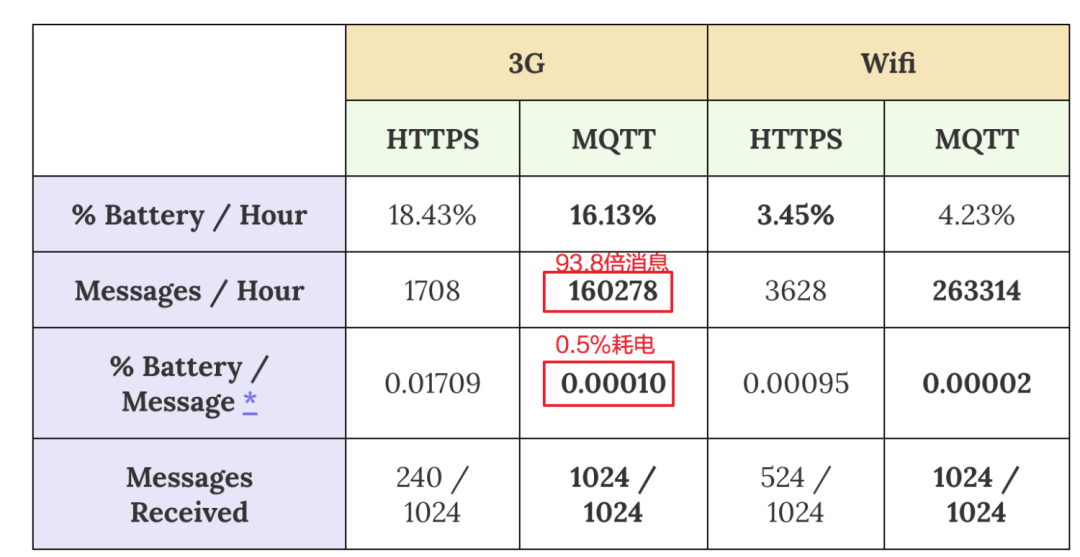
MQTT 协议概要
01 MQTT协议 MQTT(消息队列遥测传输) 是基于 TCP/IP 协议栈而构建的支持在各方之间异步通信的消息协议。MQTT在空间和时间上将消息发送者与接收者分离,因此可以在不可靠的网络环境中进行扩展。虽然叫做消息队列遥测传输,但它与消息…...

向量数据库X云计算驱动大模型落地电商行业,Zilliz联合AWS探索并贡献成熟解决方案
近日,由Zilliz 联合亚马逊云科技举办的【向量数据库 X 云计算 驱动大模型落地电商行业】活动在上海落幕,获得业内专业人士的广泛好评。 众所周知,大模型技术的发展正加速对千行万业的改革和重塑,向量数据库作为大模型的海量记忆体、云计算作为大模型的大算力平台,是大模型…...

【vue2】解决Vuex刷新页面数据丢失的问题
最近写vue2 项目需要用到vuex, 但遇到一个问题,存进store里的数据刷新就丢失了,于是乎百度解决。将自己的感受与解决方法记录下来。 数据丢失的原因 vuex存储的数据只是在页面中,相当于全局变量,页面刷新的时候vuex里的数据会重…...
小皮面板配置Xdebug,调试单个php文件
小皮面板配置Xdebug 首先下载phpstrom,和小皮面板 打开小皮面板,选中好要使用的php版本 然后点击【管理】> 【php扩展】> 【xdebug】 然后打开选中好版本的php位置 D:\Program_Files\phpstudy_pro\Extensions\php\php7.4.3nts打开php.ini文件…...
版本控制系统:Perforce Helix Core -2023
Perforce Helix Core是领先的版本控制系统,适用于需要加速大规模创新的团队。存储并跟踪您所有数字资产的更改,从源代码到二进制再到IP。连接您的团队,让他们更快地行动,更好地构建。 通过 Perforce 版本控制加速创新 Perforce H…...

回归预测 | Matlab实现基于MIC-BP最大互信息系数数据特征选择算法结合BP神经网络的数据回归预测
回归预测 | Matlab实现基于MIC-BP最大互信息系数数据特征选择算法结合BP神经网络的数据回归预测 目录 回归预测 | Matlab实现基于MIC-BP最大互信息系数数据特征选择算法结合BP神经网络的数据回归预测效果一览基本介绍研究内容程序设计参考资料 效果一览 基本介绍 Matlab实现基于…...

Hive-命令行CDH访问开启kerberos的hive
1.通过hive用户访问 切换用户为hive [rootslave conf]# su - hive 上一次登录:五 4月 12 13:59:19 CST 2019pts/1 上 [hiveslave ~]$命令行直接输入hive就可以进入hive [hiveslave ~]$ hive log4j:WARN No such property [maxFileSize] in org.apache.log4j.Dail…...
手机能搜到某个wifi,电脑搜不到解决方法(也许有用)
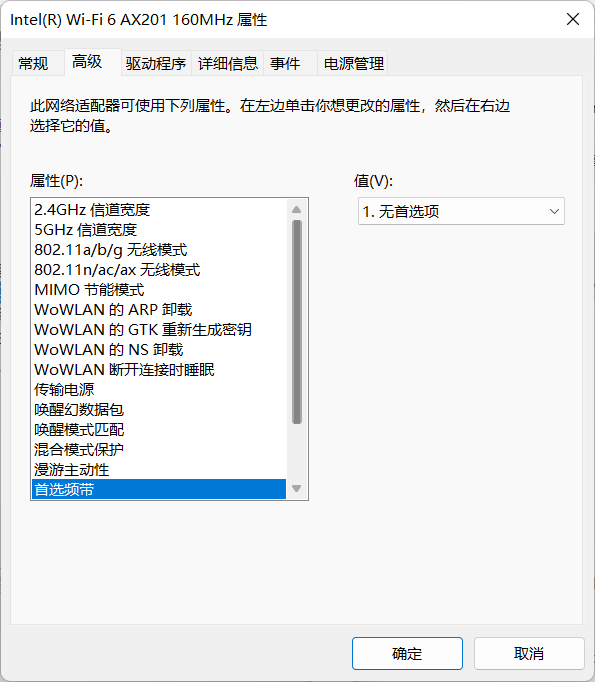
方法一:更新驱动 下载驱动大师、驱动精灵等等驱动软件,更新网卡驱动 方法二 按 win 键,打开菜单 搜索 查看网络连接(win11版本是搜这个名字) 点击打开是这样式的 然后对 WLAN右击->属性->配置->高级 这…...

Java-day18(网络编程)
网络编程 1.概述 Java提供跨平台的网络类库,可以实现无痛的网络连接,程序员面对的是一个统一的网络编程环境 网络编程的目的:直接或间接地通过网络协议与其他计算机进行通信 网络编程的两个主要问题: 1.如何准确定位网络上一台…...
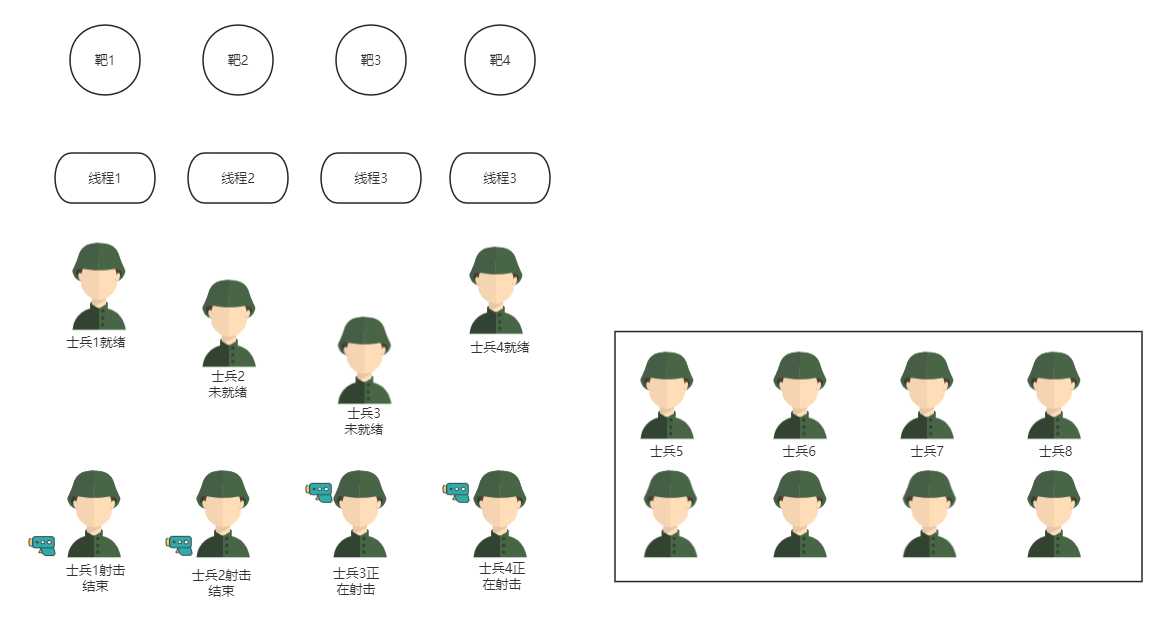
Java多线程编程-栅栏CyclicBarrier实例
前言 本文是基于《Java多线程编程实战指南-核心篇》第五章个人理解,源码是摘抄作者的源码,源码会加上自己的理解。读书笔记目前笔者正在更新如下, 《Java多线程编程实战指南-核心篇》,《How Tomcat Works》,再到《spr…...
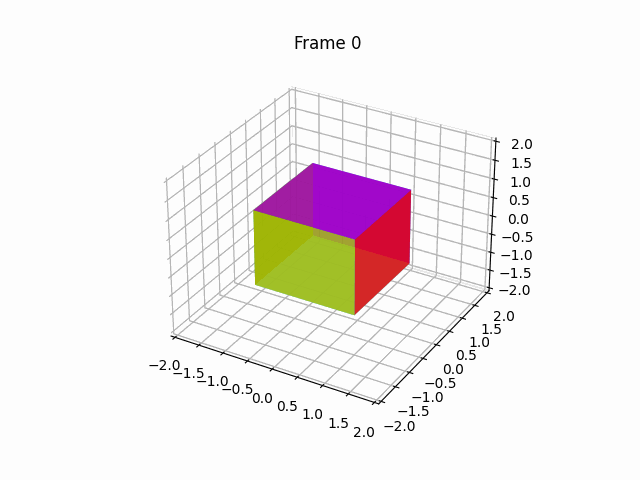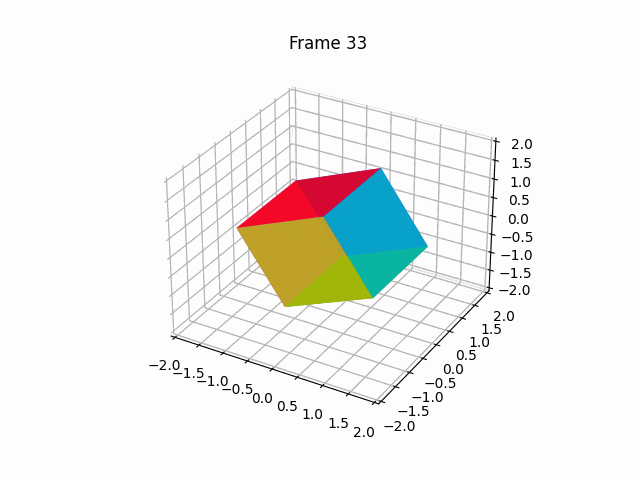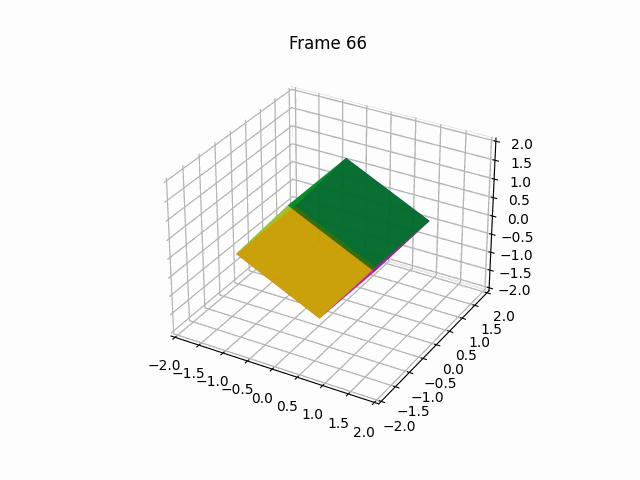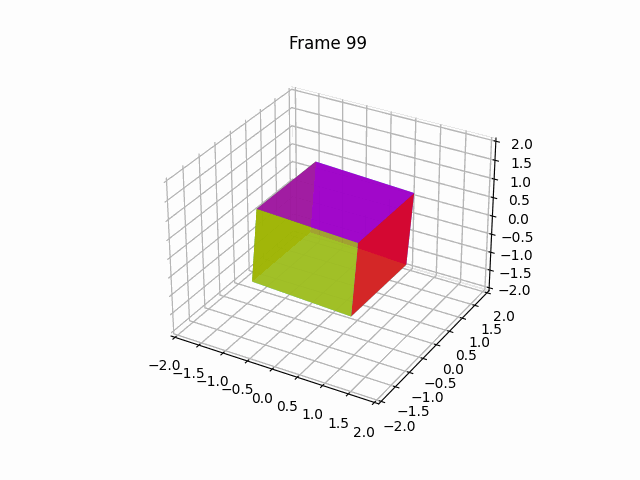
【100天精通Python】Day67:Python可视化_Matplotlib 绘制动画,2D、3D 动画 示例+代码
1 绘制2D动画(animation) Matplotlib是一个Python绘图库,它提供了丰富的绘图功能,包括绘制动画。要绘制动画,Matplotlib提供了FuncAnimation类,允许您创建基于函数的动画。下面是一个详细的Matplotlib动画示…...

变量、常量以及与其他语言的差异 - Go语言从入门到实战
知识点 源码文件以_test结尾:xxx_test.go测试方法名以Test开头:func TestXXX(t *testing.T){…} 利用单元测试来写代码段,保存之后会自动运行程序返回结果,可以快速实践得到反馈。 编写测试程序 接下来练习一下,怎…...
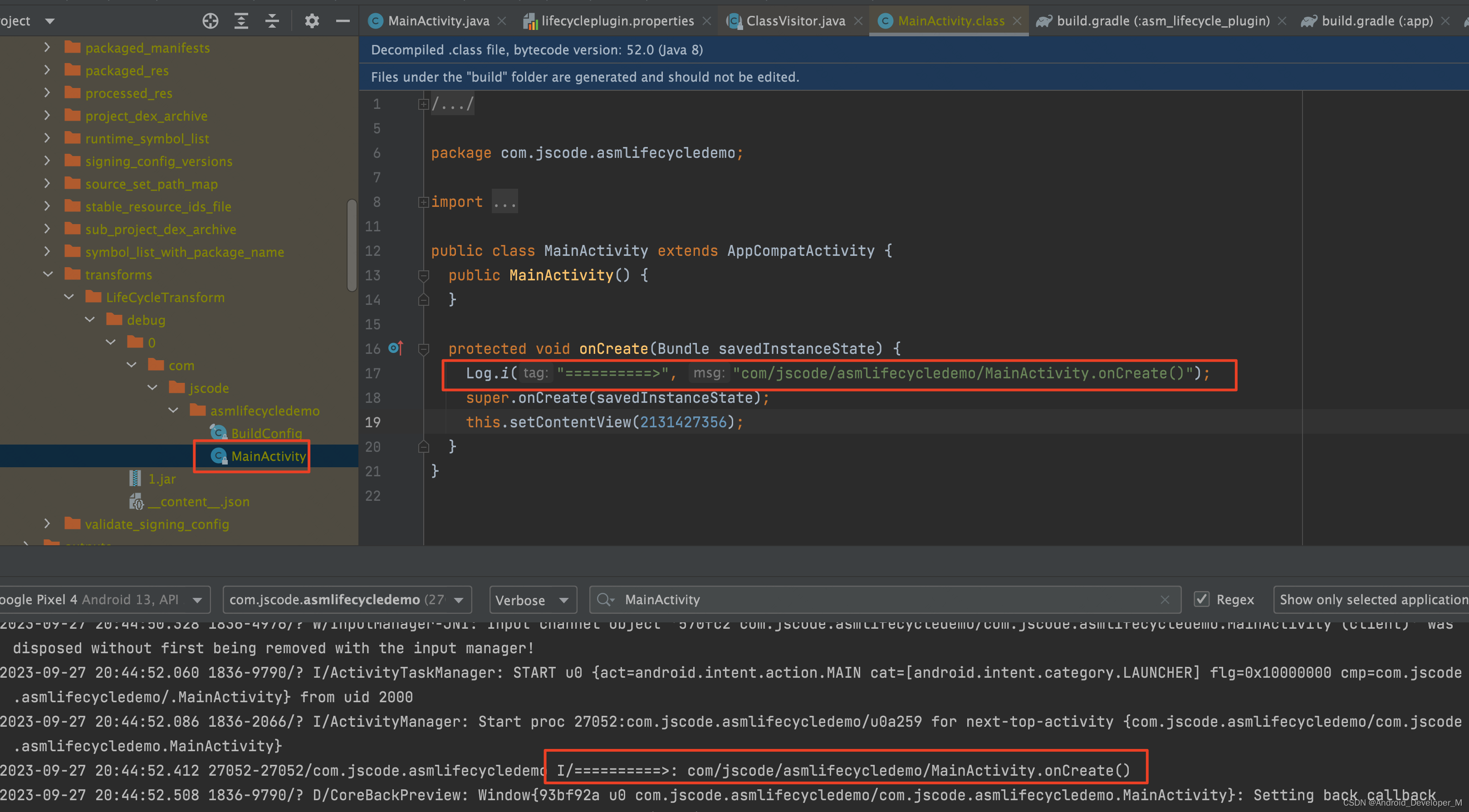
Android 编译插桩操纵字节码
本文讲解如何编译插桩操纵字节码。 就使用 ASM 来实现简单的编译插桩效果,通过插桩实现在每一个 Activity 打开时输出相应的 log 日志。实现思路 过程主要包含两步: 1、遍历项目中所有的 .class 文件 如何找到项目中编译生成的所有 .class 文件&#…...
云原生的简单理解
一、何谓云原生? 一种构建和运行应用软件的方法 应用程序从设计之初即考虑到云的环境,原生为云而设计,在云上以最佳姿势运行,充分利用和发挥云平台的弹性分布式优势。 二、包括以下四个要素 采用容器化部署:实现云平…...
AVL Cruise 2020.1 安装教程
文章目录 安装包安装破解 安装包 链接:https://pan.baidu.com/s/1GxbeDj_SyvKFyPeTsstvTQ?pwd6666 提取码:6666 安装 安装文件: 双击setup.exe: 一直netx,中间要修改两次路径,第一次是安装位置…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...

React核心概念:State是什么?如何用useState管理组件自己的数据?
系列回顾: 在上一篇《React入门第一步》中,我们已经成功创建并运行了第一个React项目。我们学会了用Vite初始化项目,并修改了App.jsx组件,让页面显示出我们想要的文字。但是,那个页面是“死”的,它只是静态…...

游戏开发中常见的战斗数值英文缩写对照表
游戏开发中常见的战斗数值英文缩写对照表 基础属性(Basic Attributes) 缩写英文全称中文释义常见使用场景HPHit Points / Health Points生命值角色生存状态MPMana Points / Magic Points魔法值技能释放资源SPStamina Points体力值动作消耗资源APAction…...
