刷题笔记26——图论二分图判定
世界上的事情,最忌讳的就是个十全十美,你看那天上的月亮,一旦圆满了,马上就要亏厌;树上的果子,一旦熟透了,马上就要坠落。凡事总要稍留欠缺,才能持恒。 ——莫言
-
visited数组是在如果有环的情况下,防止在图中一直绕圈设置的,类似于剪枝操作,走过了就没必要再走一遍
-
path是在探索过程中,记录此次的遍历路径,从而判断是否有环的
-
如果是判断的话,visited是无法判断的,path是可以判断的
-
二分图的题背会板子即可
785. 判断二分图:如果没访问就染色,访问过就判断染色是否匹配
class Solution {boolean[] visited;int[] color;boolean isB = true;public boolean isBipartite(int[][] graph) {int sz = graph.length;color = new int[sz];visited =new boolean[sz];for(int i=0;i<sz;i++){traverse(graph,i,1);}return isB;}void traverse(int[][] graph, int n, int col){if(visited[n]) return;visited[n] = true;color[n] = col;for(int node:graph[n]){if(visited[node]){if(color[node]!=(1-col)){isB = false;}}else{traverse(graph,node,1-col);}}}
}
886. 可能的二分法:有边的话就需要将两个节点分开,用二分图的思路
class Solution {// 遍历构图二分图boolean[] visited;int[] color;boolean isBi = true;public boolean possibleBipartition(int n, int[][] dislikes) {// 构造的是无向图visited = new boolean[n];color = new int[n];List<Integer>[] graph = generateGraph(n,dislikes);for(int i=0;i<n;i++){traverse(graph,i,1);}return isBi;}void traverse(List<Integer>[] graph,int n,int number){if(visited[n]) return;visited[n] = true;color[n] = number;for(int node:graph[n]){if(visited[node]){if(color[node]!=1-number){isBi = false;}}else{traverse(graph,node,1-number);}}}List<Integer>[] generateGraph(int n, int[][] dislikes){List<Integer>[] graph = new LinkedList[n];for(int i=0;i<n;i++){graph[i] = new LinkedList();}for(int i=0;i<dislikes.length;i++){graph[dislikes[i][0]-1].add(dislikes[i][1]-1);graph[dislikes[i][1]-1].add(dislikes[i][0]-1);}return graph;}
}
相关文章:

刷题笔记26——图论二分图判定
世界上的事情,最忌讳的就是个十全十美,你看那天上的月亮,一旦圆满了,马上就要亏厌;树上的果子,一旦熟透了,马上就要坠落。凡事总要稍留欠缺,才能持恒。 ——莫言 visited数组是在如果有环的情况下,防止在图中一直绕圈设置的,类似于剪枝操作,走…...

网站整站优化-网站整站优化工具
您是否曾为您的网站在搜索引擎中的排名而感到焦虑?是否苦苦思考如何提高流量、吸引更多用户? 什么是整站优化。简而言之,它是一项用于提升网站在搜索引擎中排名的策略和技巧。通过对网站的内容、结构、速度等方面进行优化,可以使…...
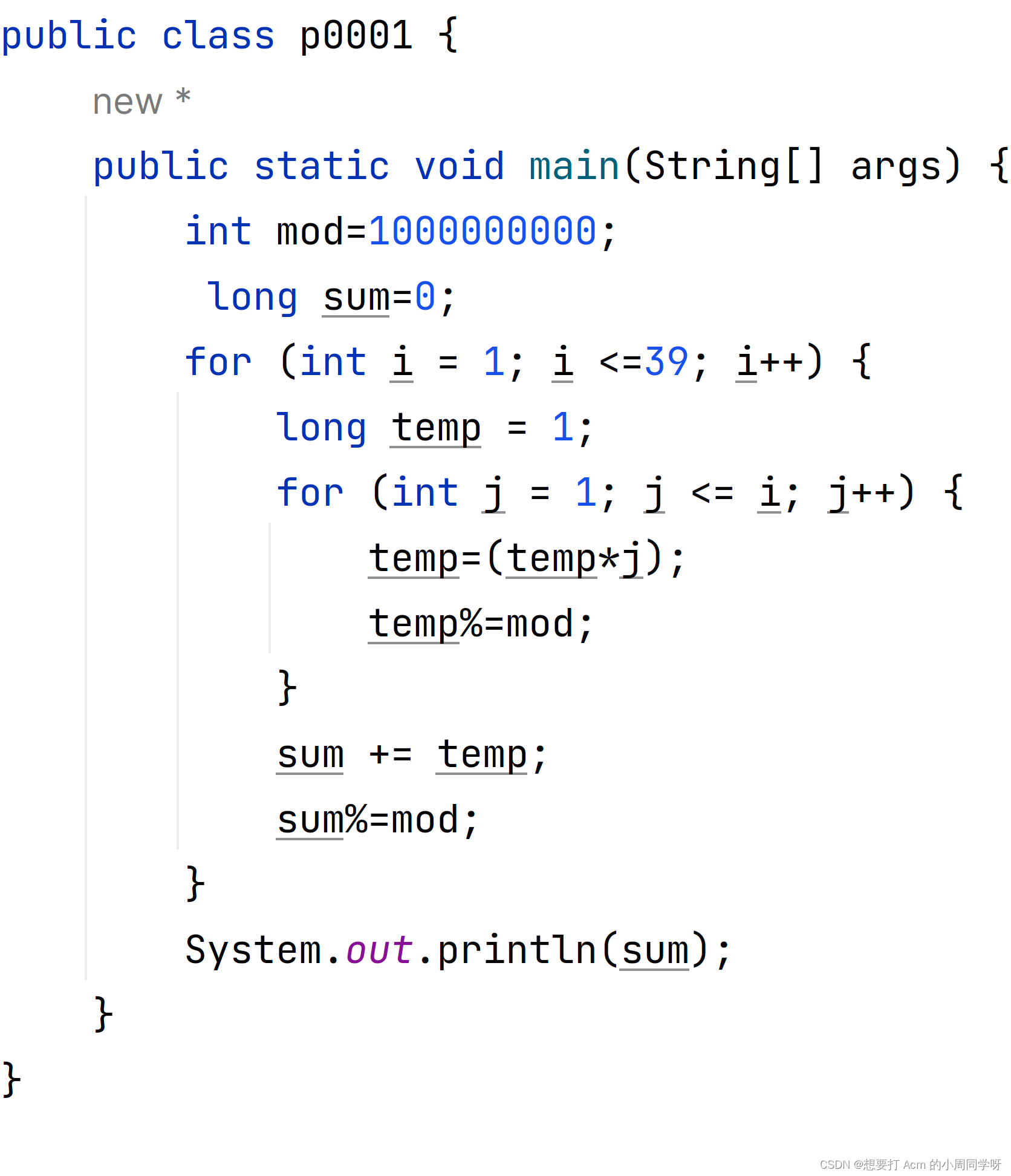
冲刺十五届蓝桥杯P0001阶乘求和
文章目录 题目描述思路分析代码解析 题目描述 思路分析 阶乘是蓝桥杯中常考的知识。 首先我们需要知道 int 和long的最大值是多少。 我们可以知道19的阶乘就已经超过了long的最大值,所以让我们直接计算202320232023!的阶乘是不现实的。 所以我们需要…...

c++ 学习 之 运算符重载
前言 运算符重载的概念: 对已有的运算符重新进行定义,赋予其另外一种功能,以适应不同的数据类型 加号运算符重载 作用:定义两个自定义的数据类型相加的运算 正常情况下,如果想要实现类中两个int 类型的相加…...

各种数据库表名长度限制整理
因为工作原因,需要整理下系统支持的数据库的表名长度限制,现发出来,以节省大家的整理时间,如有不对的敬请斧正! 数据库类型长度ORACLE 30GreenPlum40KINGBASEES63PostgreSql63Gbase63瀚高63OSCAR64MYSQL 64HBASE64Mar…...
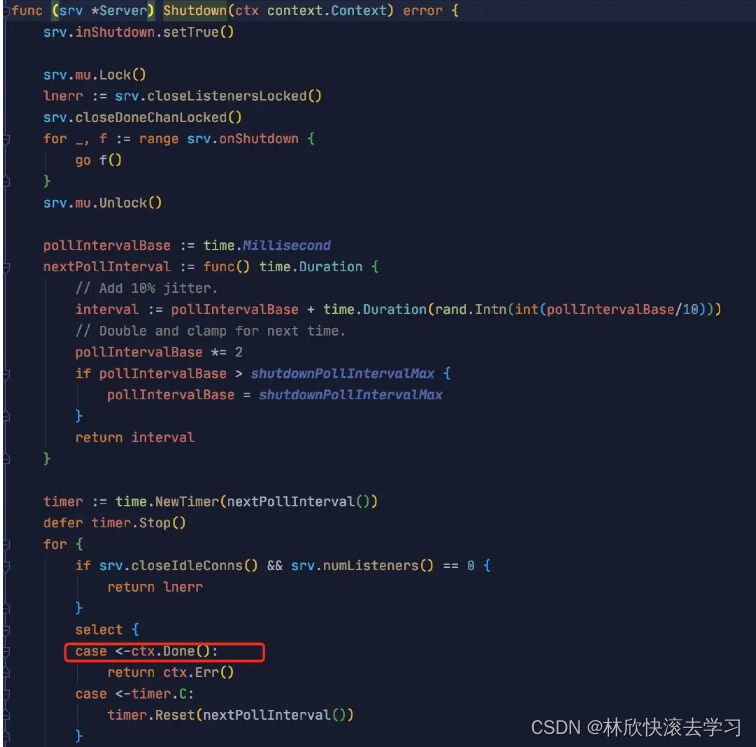
Go 里的超时控制
前言 日常开发中我们大概率会遇到超时控制的场景,比如一个批量耗时任务、网络请求等;一个良好的超时控制可以有效的避免一些问题(比如 goroutine 泄露、资源不释放等)。 Timer 在 go 中实现超时控制的方法非常简单,…...

一文彻底搞清楚Spark Schema
前言 Spark Schema定义了DataFrame的结构,可以通过对DataFrame对象调用printSchema()方法来获得该结构。Spark SQL提供了StructType和StructField类以编程方式指定架构。 默认情况下,Spark从数据中推断schema,但有时我们可能需要定义自己的schema(列名和数据类型),尤其…...

Nginx多出口IP解决代理端口数量限制,CentOS安装Nginx并开启https2.0
Nginx多出口IP解决代理端口数量限制,CentOS安装Nginx并开启https2.0。 配置文件如下: http {...upstream test {server www.test.com;}server {listen 80 default_server;server_name _;location / {proxy_pass http://test;proxy_bind $split_ip...
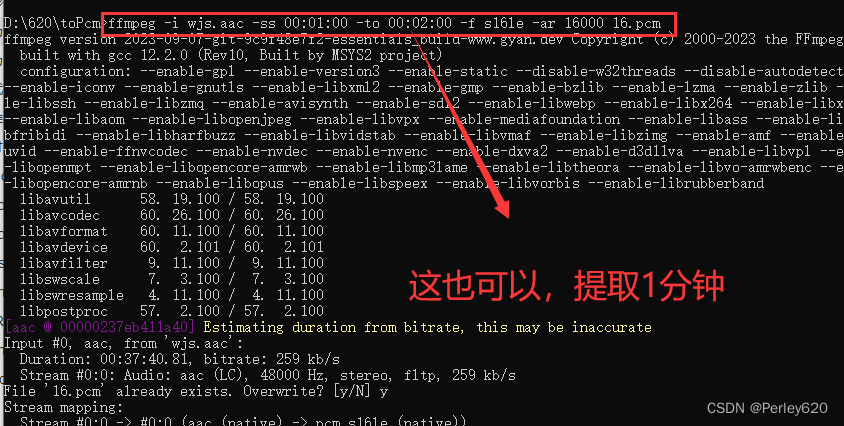
SpringBoot项目(百度AI整合)——如何在Springboot中使用语音文件识别 ffmpeg的安装和使用
前言 前言:在实际使用中,经常要参考官方的案例,但有时候因为工具的不一样,比如idea 和 eclipse,普通项目和spring项目等的差别;还有时候因为水平有限,难以在散布于官方的各个文档读懂ÿ…...

探索古彝文AI识别技术:助力中国传统文化的传承与发扬
目录 ⭐️ 写在前面 ⭐️ 一、什么是古彝文 1.1 古彝文介绍 1.2 古彝文与其他古文字示例 1.3 古彝文的重要性 ⭐️二、AI识别技术的挑战与前景 2.1 挑战 2.2 前景 ⭐️三、合合信息AI识别技术 3.1 智能文字识别技术👍👍 3.2 古文识别应用 ⭐…...

mysql面试题2:说一说MySQL的架构设计?一条 MySQL 语句执行的步骤?
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 面试官:说一说MySQL的架构设计? MySQL的架构设计主要包括以下几个组件: 连接器(Connector):负责与客户端建立连接,并进行身份验证和授权。 查询缓存…...

UPnP协议和SSDP协议
1、两种协议 UPnP协议:Universal Plug and Play,广义的即插即用。UPnP协议的目的:当有新设备连接上网络,网络上的其他设备能够马上知道有新设备加入,然后这些设备能互相宣传和发现彼此,以便能使用和控制彼…...
notepad++配置python2环境
(1)python2版本下载:Index of /ftp/python/2.7.8/https://www.python.org/ftp/python/2.7.8/ (2) 配置notepad环境 1.打开Notepad,点击“插件”-“插件管理器”,在“可用”选项卡中,…...

在ThinkAdmin中弹出层关闭后回调
在thinkadmin里面,窗口的的一些方法全部都集成在admin.js里面,在之前的文章中也有出现过类似的问题,就是对动态加载的数据进行统计,那时候写也是想记录下,现在自己都不记得是哪个站用的了,所以在这里也把这…...
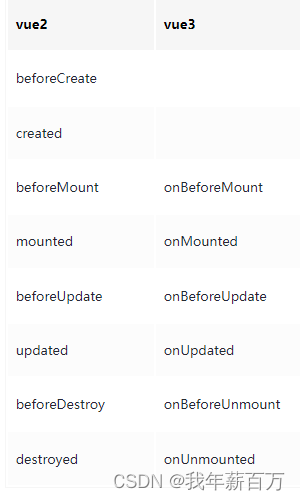
vue3 和vue2 的比较
文章目录 生命周期多根节点Composition API组合式APIOptions API与composition API对比优化逻辑组织优化逻辑复用 异步组件(Suspense)Suspense组件 响应式原理性能体积优化编译优化diff算法优化静态提升数据劫持(响应式系统)优化 生命周期 vue3在组合AP…...
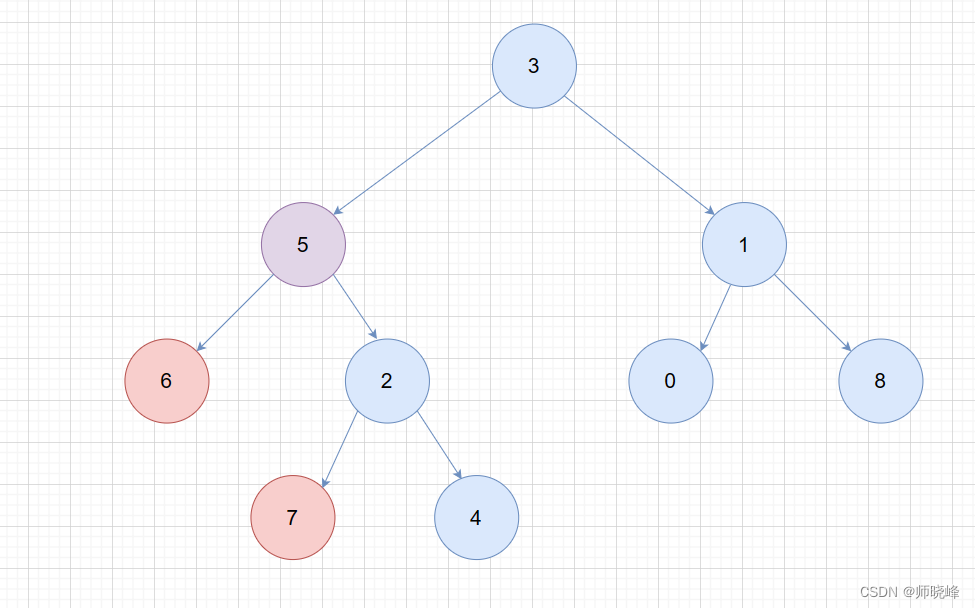
算法通过村第八关-树(深度优先)黄金笔记|寻找祖先
文章目录 前言最近公共祖先问题总结 前言 提示:生活就是一场有很多规则,却没有裁判的比赛。 --约瑟夫布罗茨基《悲伤与理智》 最近公共祖先问题 参考题目地址:236. 二叉树的最近公共祖先 - 力扣(LeetCode) 如果将搜索…...
postgresql|数据库|数据库测试工具pgbench之使用
前言: 数据库是项目中的重要组件,也是一个基础的重要组件,其地位说是第一我想应该是没有什么太多问题的。 那么,数据库的设计这些方面是不用多说的,关键的第一步,主要是涉及数据库的部署方式,…...

代码随想录Day51 | 309.最佳买卖股票时机含冷冻期
309. 买卖股票的最佳时机含冷冻期 class Solution { public:int maxProfit(vector<int>& prices) {int n prices.size();if (n 0) return 0;vector<vector<int>> dp(n, vector<int>(4, 0));dp[0][0] - prices[0]; // 持股票for (int i 1; i &l…...

libopenssl 实现私钥加密公钥解密
在需要验证可信来源时,需要用到签名验签。因此,需要使用私钥加密,公钥解密,取得被加密的信息。这就会使用到私钥加密,公钥解密的场景了。 参考: https://github.com/openssl/openssl/issues/20493 https:/…...

代码随想录 Day - 51|#309 最佳买卖股票时机含冷冻期|#714 买卖股票的最佳时机含手续费
清单 ● 309.最佳买卖股票时机含冷冻期 ● 714.买卖股票的最佳时机含手续费 LeetCode #309 最佳买卖股票时机含冷冻期 1. 题目 给定一个整数数组,其中第 i 个元素代表了第 i 天的股票价格 。 设计一个算法计算出最大利润。在满足以下约束条件下,你可…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

深度解析:etcd 在 Milvus 向量数据库中的关键作用
目录 🚀 深度解析:etcd 在 Milvus 向量数据库中的关键作用 💡 什么是 etcd? 🧠 Milvus 架构简介 📦 etcd 在 Milvus 中的核心作用 🔧 实际工作流程示意 ⚠️ 如果 etcd 出现问题会怎样&am…...
