当前位置： 首页 > news >正文

秋招算法岗，面试复盘

news 2025/7/5 22:14:00

d85635c77cb7cf16ed2bf11528963572.jpeg

面试锦囊之面经分享系列，持续更新中 c90f339d9419f3b28bb31d641688b764.png

欢迎后台回复『面试』加入讨论组交流噢 db7334718f4859f61e138000b342025c.png

楼主秋招主要投算法岗（偏NLP方向）和数据岗方向，下面分享我的一些面试经历。

一、科大讯飞（NLP）

  1. 简要介绍自己

  2. Python里面哈希表对应哪种结构，是如何解决哈希冲突的

  3. DSSM模型和ESIM模型的区别

  4. Word2vec原理，word2vec和fasttext原理上的区别

  5. Bert原理，bert随机mask掉15%的词，为什么要随机有80%替换为【mask】，10%要替换为别的单词，随机10%不替换

  6. 文本匹配怎么使用bert

  7. 实习里的项目

  8. Xgb原理

  9. 编程题：找无序数量的中位数，时间复杂度比排序要快

二、字节跳动（广告算法）

  1. AUC的原理（衡量分类器排序的能力），计算（100正，900负，分类器是0到1均匀分布，计算AUC）

  2. 样本不平衡如何改进，影响了样本原本的分布该怎么办

相关文章：

秋招算法岗，面试复盘

面试锦囊之面经分享系列，持续更新中 欢迎后台回复『面试』加入讨论组交流噢 楼主秋招主要投算法岗（偏NLP方向）和数据岗方向，下面分享我的一些面试经历。 一、科大讯飞（NLP） 简要介绍自己Python里面哈希表…...

编程日记 2023/9/29 7:06:06

AI类APP能做什么

AI类APP可以实现多种功能，涵盖了各种领域和用途。以下是一些常见的AI类APP示例以及它们主要实现的功能，希望对大家有所帮助。北京木奇移动技术有限公司，专业的软件外包开发公司，欢迎交流合作。 1.语音助手（Voice Assis…...

编程日记 2023/9/29 7:03:03

计算机毕业设计 基于SSM的垃圾分类管理系统（以医疗垃圾为例）的设计与实现 Java实战项目 附源码+文档+视频讲解

博主介绍：✌从事软件开发10年之余，专注于Java技术领域、Python人工智能及数据挖掘、小程序项目开发和Android项目开发等。CSDN、掘金、华为云、InfoQ、阿里云等平台优质作者✌ 🍅文末获取源码联系🍅 👇🏻 精…...

编程日记 2023/9/29 7:01:01

友思特案例｜友思特 Ensenso 3D相机：汽车工业自动化的革命性力量

01 内容摘要 在竞争激烈的汽车行业，自动化生产至关重要。友思特 Ensenso 3D相机为汽车制造商提供了可靠的工具和技术支持，助力多个关键环节。它在汽车座位泡棉切割中提高精确度，降低浪费，提高生产效率；在汽车压铸零部…...

编程日记 2023/9/29 6:57:58

【5G PHY】物理层逻辑和物理天线的映射

博主未授权任何人或组织机构转载博主任何原创文章，感谢各位对原创的支持！ 博主链接 本人就职于国际知名终端厂商，负责modem芯片研发。 在5G早期负责终端数据业务层、核心网相关的开发工作，目前牵头6G算力网络技术标准研究。 博客…...

编程日记 2023/9/29 6:56:56

MySQL如何优雅处理批量新增和更新?ON DUPLICATE KEY UPDATE用它!

场景：一张用户表user，此时我需要批量新增用户，如果用户已经存在了，则更新该条记录；如果用户不存在，则插入一条数据。 痛点：常规做法新增更新各写一个接口。而且是批量操作，比较繁琐&…...

编程日记 2023/9/29 6:55:56

网络安全(加密, Hashing, 证书, SSL/TLS等)学习小结

网上看到的一些关于网络安全的学习资料小结。 对称加密: 通信双方共享同一个密钥。发送方用它来加密，接收方用它来解密。 非对称加密: 有公钥和私钥。 现在的做法一般是用非对称加密生成？钥(公钥还是私钥?）用于传输？&#xff0…...

编程日记 2023/9/29 6:50:52

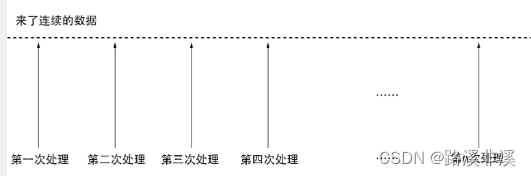
缓冲技术在嵌入式中的应用

引言 在嵌入式中，不可避免地会遇到数据的收发。 其实，数据的收发有很多情况。 总体上，分为数据的收和发： 其中，数据发送是一个主动的行为，我们对要发送数据的数量特点等都是知道的，比如我们通过…...

编程日记 2023/9/29 6:49:51

vscode交叉编译cmake工程，toolchains设置

在 Visual Studio Code 中编译 CMake 项目时，使用自定义工具链（toolchains）可以很有用，特别是当你需要交叉编译或使用不同的编译器时。以下是在 Visual Studio Code 中使用自定义工具链的一般步骤，以aarch64的嵌入式为…...

编程日记 2023/9/29 6:46:48

MATLAB算法实战应用案例精讲-【优化算法】季节优化算法(SOA)(附MATLAB代码实现)

前言 世界上许多地方一年有四个季节:春、夏、秋、冬。每个季节的天气都不一样。随着天气的变化，生物，尤其是树木会改变它们的行为来适应天气。森林中的每一个个体都被称为一棵树。在满足终止条件之前，森林中的树木通过类似于自然界树木生命周期的四种操作:更新、竞争、播种…...

编程日记 2023/9/29 6:45:47

DevOps持续集成与交付

概述 Jenkins是一个支持容器化部署的、使用Java运行环境的开源软件，使用Jenkins平台可以定制化不同的流程与任务、以自动化的机制支持DevOps领域中的CI与CD，在软件开发与运维的流程中自动化地执行软件工程项目的编译、构建、打包、测试、发布以及部署&a…...

编程日记 2023/9/29 6:44:46

lambda的使用案例（1）

lambda的使用案例 1、分组转换为map Map<String, List<IdaasUserInfoVO>> map userWithOrgVOS1.stream().collect(Collectors.groupingBy(IdaasUserInfoVO::getOrgId));2、map循环 map.forEach(this::saveOrUpdateUser); private void saveOrUpdateUser(String …...

编程日记 2023/9/29 6:43:45

nodejs+vue装修公司CRM系统设计elementui

第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性&#xff1a;技术背景 5 3.2.2经济可行性 6 3.2.3操作可行性&#xff1a; 6 3.3 项目设计目标与原则 6 3.4系统流程分析 7 3.4.1操作流程 7 3.4.2添加信息流程 8 3.4.3删除信息流程 9 第4章 系统设计 11 …...

编程日记 2023/9/29 6:42:44

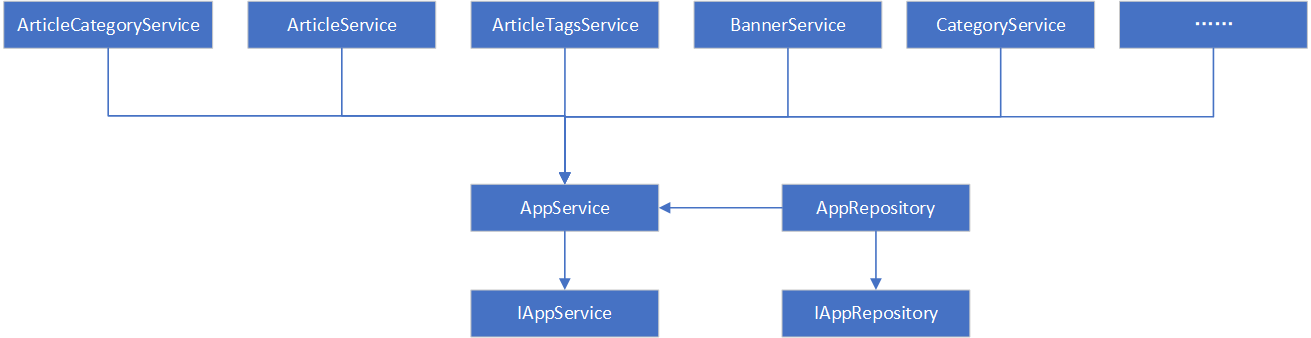
开源博客项目Blog .NET Core源码学习（3：数据库操作方式）

开源博客项目Blog采用SqlSugar模块连接并操作数据库&#xff0c;本文学习并记录项目中使用SqlSugar的方式和方法。   首先&#xff0c;数据库连接信息放在了App.Hosting项目的appsettings.json中DbConfig节&#xff0c;支持在DbConfig节配置多个数据库连接信息&#xff0c;以…...

编程日记 2023/9/29 6:41:44

QT--Opencv下报错Mat/imwrite/imread找不到文件

像file not found这类错误 原因是编程系统找不到所指库文件&#xff0c;以此为例&#xff0c;排查自己的每个位置是否有误 1. .pro文件 添加opencv动态库 INCLUDEPATH /usr/include \/usr/include/opencv4 \/usr/include/opencv4/opencv2LIBS /usr/lib/aarch64-linux-gnu…...

编程日记 2023/9/29 6:40:43

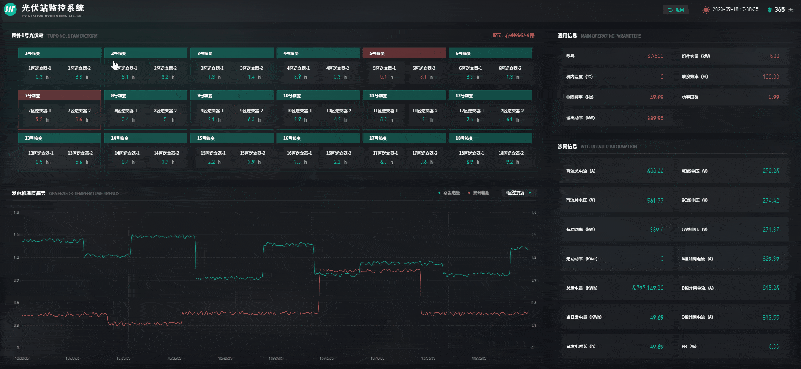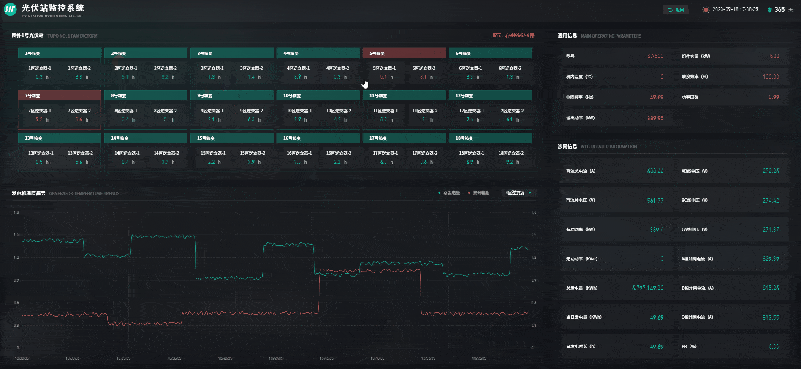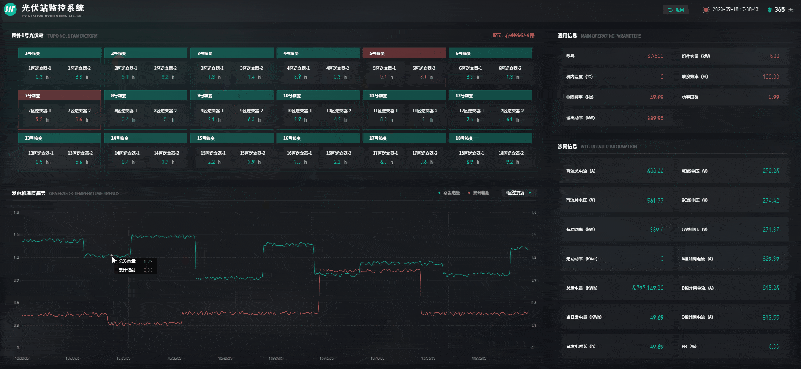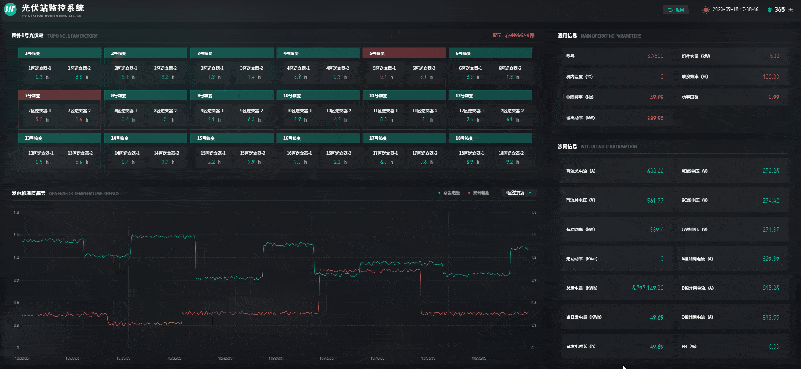
风光储一体化能源中心 | 数字孪生智慧能源

自“双碳”目标提出以来&#xff0c;我国能源产业不断朝着清洁低碳化、绿色化的方向发展。其中&#xff0c;风能、太阳能等可再生能源在促进全球能源可持续发展、共建清洁美丽世界中被寄予厚望。风能、太阳能具有波动性、间歇性、随机性等特点&#xff0c;主要通过转化为电能再…...

编程日记 2023/9/29 6:39:42

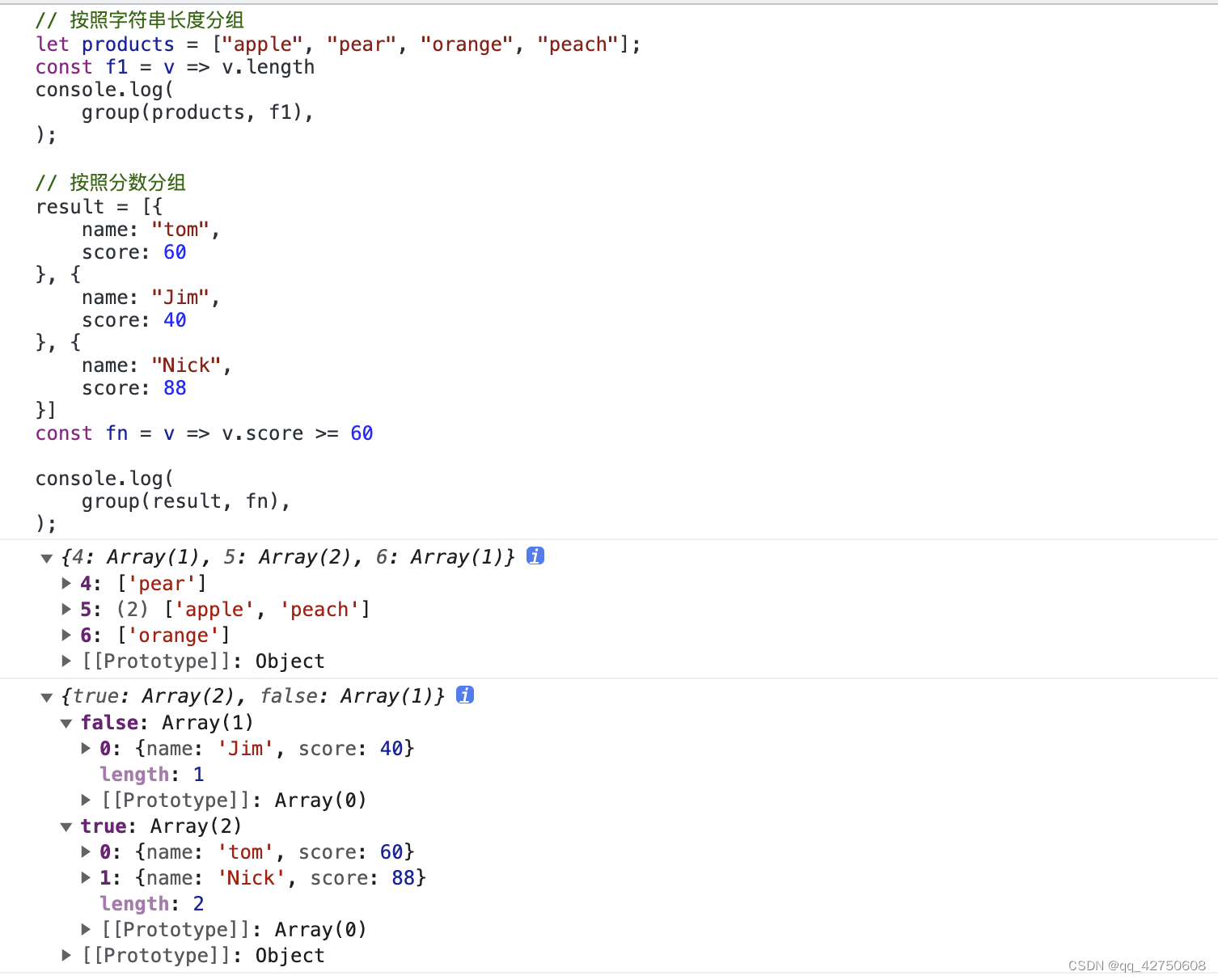
JavaScript数组分组

数组分组: 含义: 数据按照某个特性归类 1. reducefn(cur, index)作为对象的key,值为按照fn筛选出来的数据 // 利用reduce分组 function group(arr, fn) {// 不是数组if (!Array.isArray(arr)) {return arr}// 不是函数if (typeof fn ! function) {throw new TypeError(fn…...

编程日记 2023/9/29 6:38:41

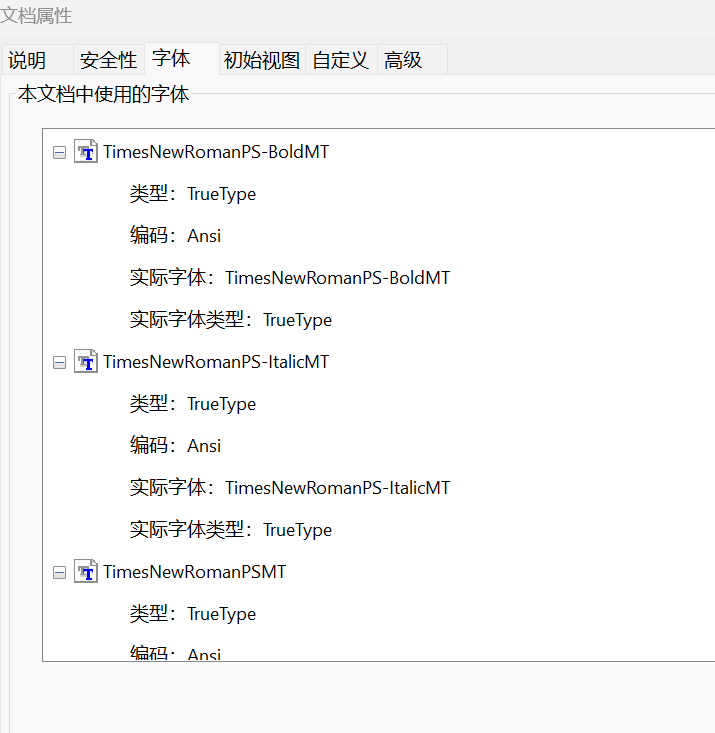
IEEE PDF eXpress系统报错：TimesNewRoman PS-BoldMT, ItalicMT, PSM

问题&#xff1a; IEEE PDF eXpress系统报错&#xff1a;Errors: Font TimesNewRomanPS-BoldMT, TimesNewRomanPS-ItalicMT, TimesNewRomanPSMT is not embedded (137x on pages 2-6) 答案&#xff1a; 主要原因是PDF的字体嵌入问题&#xff0c;可以看到下图中没有报错中的字体…...

编程日记 2023/9/29 6:36:38

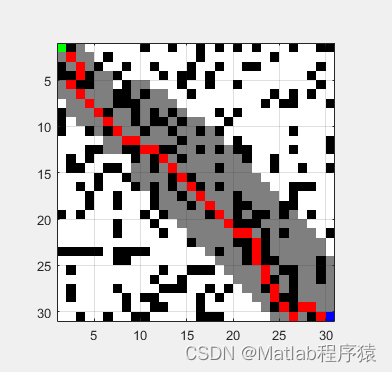
【MATLAB源码-第40期】基于matlab的D*(Dstar)算法栅格路径规划仿真。

1、算法描述 D*算法路径规划 D*算法&#xff08;Dynamic A*&#xff09;是A*算法的一种变种&#xff0c;主要用于在地图中的障碍物信息发生变化时重新计算路径&#xff0c;而不需要从头开始。该算法适用于那些只有部分信息已知的环境中。 工作原理&#xff1a; 1. D*算法首先…...

编程日记 2023/9/29 6:35:37

Pikachu-xxe （xml外部实体注入漏洞）过关笔记

Pikachu-xxe过关笔记 有回显探测是否有回显file:///协议查看本地系统文件php://协议查看php源代码&#xff08;无法查看当前网页代码&#xff0c;只能看别的&#xff09;http://协议爆破开放端口&#xff08;两者的加载时间不同&#xff09; 无回显第一步第二步第三步 运行结果…...

编程日记 2023/9/29 6:30:33

汽车生产虚拟实训中的技能提升与生产优化​

在制造业蓬勃发展的大背景下&#xff0c;虚拟教学实训宛如一颗璀璨的新星&#xff0c;正发挥着不可或缺且日益凸显的关键作用&#xff0c;源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例&#xff0c;汽车生产线上各类…...

编程新知 2025/7/4 8:53:19

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序

一、开发准备 ​​环境搭建​​&#xff1a; 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 ​​项目创建​​&#xff1a; File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

编程新知 2025/7/4 7:22:38

postgresql|数据库|只读用户的创建和删除（备忘）

CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

编程新知 2025/6/21 18:39:26

页面渲染流程与性能优化

页面渲染流程与性能优化详解&#xff08;完整版&#xff09; 一、现代浏览器渲染流程&#xff08;详细说明&#xff09; 1. 构建DOM树 浏览器接收到HTML文档后&#xff0c;会逐步解析并构建DOM&#xff08;Document Object Model&#xff09;树。具体过程如下&#xff1a; (…...

编程新知 2025/6/26 7:14:46

vue3 定时器-定义全局方法 vue+ts

1.创建ts文件 路径&#xff1a;src/utils/timer.ts 完整代码&#xff1a; import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

编程新知 2025/7/5 18:26:46

令牌桶 滑动窗口-＞限流 分布式信号量-＞限并发的原理 lua脚本分析介绍

文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结&#xff1a; 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析&#xff1a; 实际业务去理解体会统一注…...

编程新知 2025/7/4 19:57:27

自然语言处理——Transformer

自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效&#xff0c;它能挖掘数据中的时序信息以及语义信息&#xff0c;但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN&#xff0c;但是…...

编程新知 2025/6/21 6:23:38

UR 协作机器人「三剑客」：精密轻量担当（UR7e）、全能协作主力（UR12e）、重型任务专家（UR15）

UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中&#xff0c;UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化&#xf…...

编程新知 2025/6/24 6:19:04

Caliper 配置文件解析：config.yaml

Caliper 是一个区块链性能基准测试工具，用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构，并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件，主要包含以下几个部…...

编程新知 2025/6/20 18:29:18

如何理解 IP 数据报中的 TTL？

目录 前言理解 前言 面试灵魂一问&#xff1a;说说对 IP 数据报中 TTL 的理解&#xff1f;我们都知道&#xff0c;IP 数据报由首部和数据两部分组成&#xff0c;首部又分为两部分&#xff1a;固定部分和可变部分&#xff0c;共占 20 字节&#xff0c;而即将讨论的 TTL 就位于首…...

编程新知 2025/6/26 9:15:41