Hoeffing不等式
在李航老师的统计学习方法(第一版中) H o e f f i n g 不等式 Hoeffing不等式 Hoeffing不等式是这样子给出的
设 X 1 , X 2 , . . . , X N X_1,X_2,...,X_N X1,X2,...,XN是独立随机变量,且 X i ∈ [ a i , b i ] , i = 1 , 2 , . . . , N ; S N = ∑ i = 1 N X i X_i\in[a_i,b_i],i=1,2,...,N;S_N=\sum_{i=1}^NX_i Xi∈[ai,bi],i=1,2,...,N;SN=∑i=1NXi,则对任意t>0,以下不等式成立:
P [ S N − E ( S N ) ≥ t ] ≤ e x p [ − 2 t 2 ∑ i = 1 N ( b i − a i ) 2 ] P[S_N-E(S_N)≥t]≤exp[-\frac{2t^2}{\sum_{i=1}^N(b_i-a_i)^2}] P[SN−E(SN)≥t]≤exp[−∑i=1N(bi−ai)22t2]
P [ E ( S N ) − S N ≥ t ] ≤ e x p [ − 2 t 2 ∑ i = 1 N ( b i − a i ) 2 ] P[E(S_N)-S_N≥t]≤exp[-\frac{2t^2}{\sum_{i=1}^N(b_i-a_i)^2}] P[E(SN)−SN≥t]≤exp[−∑i=1N(bi−ai)22t2]
这两个数学公式是关于独立随机变量和它们的和的Hoeffding不等式的表达式。它们用于估计随机变量和与其期望之间的差异的概率上界。让我解释这些不等式的含义:
假设有 N N N 个独立随机变量 X 1 , X 2 , … , X N X_1, X_2, \ldots, X_N X1,X2,…,XN,其中每个 X i X_i Xi 的取值范围位于区间 [ a i , b i ] [a_i, b_i] [ai,bi] 内,即 a i ≤ X i ≤ b i a_i \leq X_i \leq b_i ai≤Xi≤bi,并且它们是彼此独立的。我们定义一个随机变量 S N S_N SN,表示这些随机变量的和,即 S N = ∑ i = 1 N X i S_N = \sum_{i=1}^N X_i SN=∑i=1NXi。同时,我们有 E ( S N ) E(S_N) E(SN) 表示 S N S_N SN 的期望值,即 E ( S N ) = ∑ i = 1 N E [ X i ] E(S_N) = \sum_{i=1}^N \mathbb{E}[X_i] E(SN)=∑i=1NE[Xi]。
现在,这两个不等式分别描述了以下情况:
- 第一个不等式:
P [ S N − E ( S N ) ≥ t ] ≤ exp ( − 2 t 2 ∑ i = 1 N ( b i − a i ) 2 ) P[S_N - E(S_N) \geq t] \leq \exp\left(-\frac{2t^2}{\sum_{i=1}^N (b_i - a_i)^2}\right) P[SN−E(SN)≥t]≤exp(−∑i=1N(bi−ai)22t2)
这个不等式表示随机变量和 S N S_N SN 超过其期望值 E ( S N ) E(S_N) E(SN) 的值大于或等于 t t t 的概率不会超过 exp ( − 2 t 2 ∑ i = 1 N ( b i − a i ) 2 ) \exp\left(-\frac{2t^2}{\sum_{i=1}^N (b_i - a_i)^2}\right) exp(−∑i=1N(bi−ai)22t2)。换句话说,它提供了一个关于 S N S_N SN 偏离其期望值的概率上界。
- 第二个不等式:
P [ E ( S N ) − S N ≥ t ] ≤ exp ( − 2 t 2 ∑ i = 1 N ( b i − a i ) 2 ) P[E(S_N) - S_N \geq t] \leq \exp\left(-\frac{2t^2}{\sum_{i=1}^N (b_i - a_i)^2}\right) P[E(SN)−SN≥t]≤exp(−∑i=1N(bi−ai)22t2)
这个不等式表示随机变量和 S N S_N SN 低于其期望值 E ( S N ) E(S_N) E(SN) 的值大于或等于 t t t 的概率不会超过 exp ( − 2 t 2 ∑ i = 1 N ( b i − a i ) 2 ) \exp\left(-\frac{2t^2}{\sum_{i=1}^N (b_i - a_i)^2}\right) exp(−∑i=1N(bi−ai)22t2)。它提供了一个关于 S N S_N SN 偏离其期望值的概率上界,但是方向与第一个不等式相反。
这些不等式是Hoeffding不等式的一种形式,它们可用于估计随机变量和的性质以及样本统计的可靠性。不等式的右侧是关于样本范围 [ a i , b i ] [a_i, b_i] [ai,bi] 的性质和观察样本数量 N N N 的函数,它们决定了概率上界的大小。这些不等式对于分析随机过程和估计样本均值的可信度非常有用。
在李航老师统计学习方法(第二版中)是这样子给出
设 X 1 , X 2 , . . . , X N X_1,X_2,...,X_N X1,X2,...,XN是独立随机变量,且 X i ∈ [ a i , b i ] , i = 1 , 2 , . . . , N ; X ˉ X_i\in[a_i,b_i],i=1,2,...,N;\bar{X} Xi∈[ai,bi],i=1,2,...,N;Xˉ是 X 1 , X 2 , . . . , X N X_1,X_2,...,X_N X1,X2,...,XN的经验均值, X ˉ = 1 N ∑ i = 1 N X i \bar{X}=\frac{1}{N}\sum_{i=1}^NX_i Xˉ=N1∑i=1NXi ,则对任意t>0,以下不等式成立
P [ X ˉ − E ( X ˉ ) ≥ t ] ≤ exp ( − 2 N 2 t 2 ∑ i = 1 N ( b i − a i ) 2 ) P[\bar{X} - E(\bar{X}) \geq t] \leq \exp\left(-\frac{2N^2t^2}{\sum_{i=1}^N (b_i - a_i)^2}\right) P[Xˉ−E(Xˉ)≥t]≤exp(−∑i=1N(bi−ai)22N2t2)
P [ E ( X ˉ ) − X ˉ ≥ t ] ≤ exp ( − 2 N 2 t 2 ∑ i = 1 N ( b i − a i ) 2 ) P[E(\bar{X}) - \bar{X} \geq t] \leq \exp\left(-\frac{2N^2t^2}{\sum_{i=1}^N (b_i - a_i)^2}\right) P[E(Xˉ)−Xˉ≥t]≤exp(−∑i=1N(bi−ai)22N2t2)
这两个不等式是关于经验均值(样本均值) X ˉ \bar{X} Xˉ 与其期望值 E ( X ˉ ) E(\bar{X}) E(Xˉ) 之间的差异的概率上界,这些差异由Hoeffding不等式提供。让我解释这些不等式的含义:
假设有 N N N 个独立随机变量 X 1 , X 2 , … , X N X_1, X_2, \ldots, X_N X1,X2,…,XN,其中每个 X i X_i Xi 的取值范围位于区间 [ a i , b i ] [a_i, b_i] [ai,bi] 内,即 a i ≤ X i ≤ b i a_i \leq X_i \leq b_i ai≤Xi≤bi,并且它们是彼此独立的。我们定义一个随机变量 X ˉ \bar{X} Xˉ,表示这些随机变量的经验均值(样本均值),即 X ˉ = 1 N ∑ i = 1 N X i \bar{X} = \frac{1}{N}\sum_{i=1}^N X_i Xˉ=N1∑i=1NXi。
现在,这两个不等式分别描述了以下情况:
- 第一个不等式:
P [ X ˉ − E ( X ˉ ) ≥ t ] ≤ exp ( − 2 N 2 t 2 ∑ i = 1 N ( b i − a i ) 2 ) P[\bar{X} - E(\bar{X}) \geq t] \leq \exp\left(-\frac{2N^2t^2}{\sum_{i=1}^N (b_i - a_i)^2}\right) P[Xˉ−E(Xˉ)≥t]≤exp(−∑i=1N(bi−ai)22N2t2)
这个不等式表示经验均值 X ˉ \bar{X} Xˉ 超过其期望值 E ( X ˉ ) E(\bar{X}) E(Xˉ) 的值大于或等于 t t t 的概率不会超过 exp ( − 2 N 2 t 2 ∑ i = 1 N ( b i − a i ) 2 ) \exp\left(-\frac{2N^2t^2}{\sum_{i=1}^N (b_i - a_i)^2}\right) exp(−∑i=1N(bi−ai)22N2t2)。换句话说,它提供了一个关于经验均值 X ˉ \bar{X} Xˉ 偏离其期望值 E ( X ˉ ) E(\bar{X}) E(Xˉ) 的概率上界。
- 第二个不等式:
P [ E ( X ˉ ) − X ˉ ≥ t ] ≤ exp ( − 2 N 2 t 2 ∑ i = 1 N ( b i − a i ) 2 ) P[E(\bar{X}) - \bar{X} \geq t] \leq \exp\left(-\frac{2N^2t^2}{\sum_{i=1}^N (b_i - a_i)^2}\right) P[E(Xˉ)−Xˉ≥t]≤exp(−∑i=1N(bi−ai)22N2t2)
这个不等式表示经验均值 X ˉ \bar{X} Xˉ 低于其期望值 E ( X ˉ ) E(\bar{X}) E(Xˉ) 的值大于或等于 t t t 的概率不会超过 exp ( − 2 N 2 t 2 ∑ i = 1 N ( b i − a i ) 2 ) \exp\left(-\frac{2N^2t^2}{\sum_{i=1}^N (b_i - a_i)^2}\right) exp(−∑i=1N(bi−ai)22N2t2)。它提供了一个关于经验均值 X ˉ \bar{X} Xˉ 偏离其期望值 E ( X ˉ ) E(\bar{X}) E(Xˉ) 的概率上界,但方向与第一个不等式相反。
这些不等式是Hoeffding不等式的一种形式,它们可用于估计经验均值的性质以及样本统计的可靠性。不等式的右侧是关于样本范围 [ a i , b i ] [a_i, b_i] [ai,bi] 的性质和观察样本数量 N N N 的函数,它们决定了概率上界的大小。这些不等式对于分析随机过程和估计样本均值的可信度非常有用。
如何从第一版推理到第二版
要从第一组不等式推导出第二组不等式,您可以使用一些基本的概率论和数学推导的技巧。下面是一种可能的推导方法:
首先,我们有 S N = ∑ i = 1 N X i S_N = \sum_{i=1}^N X_i SN=∑i=1NXi,并且 X ˉ = 1 N S N \bar{X} = \frac{1}{N}S_N Xˉ=N1SN。因此,我们可以将 S N S_N SN 表示为 X ˉ \bar{X} Xˉ 的形式:
S N = N ⋅ X ˉ S_N = N \cdot \bar{X} SN=N⋅Xˉ
接下来,让我们考虑第一个不等式:
P [ S N − E ( S N ) ≥ t ] ≤ exp ( − 2 t 2 ∑ i = 1 N ( b i − a i ) 2 ) P[S_N - E(S_N) \geq t] \leq \exp\left(-\frac{2t^2}{\sum_{i=1}^N (b_i - a_i)^2}\right) P[SN−E(SN)≥t]≤exp(−∑i=1N(bi−ai)22t2)
现在用 S N = N ⋅ X ˉ S_N = N \cdot \bar{X} SN=N⋅Xˉ 和 E ( S N ) = N ⋅ E ( X ˉ ) E(S_N) = N \cdot E(\bar{X}) E(SN)=N⋅E(Xˉ) 替换右侧的 S N S_N SN 和 E ( S N ) E(S_N) E(SN):
P [ N ⋅ X ˉ − N ⋅ E ( X ˉ ) ≥ t ] ≤ exp ( − 2 t 2 ∑ i = 1 N ( b i − a i ) 2 ) P[N \cdot \bar{X} - N \cdot E(\bar{X}) \geq t] \leq \exp\left(-\frac{2t^2}{\sum_{i=1}^N (b_i - a_i)^2}\right) P[N⋅Xˉ−N⋅E(Xˉ)≥t]≤exp(−∑i=1N(bi−ai)22t2)
然后,我们可以将 N N N 提取出来,并且在不等式两侧都除以 N N N,得到:
P [ X ˉ − E ( X ˉ ) ≥ t N ] ≤ exp ( − 2 t 2 ∑ i = 1 N ( b i − a i ) 2 ) P[\bar{X} - E(\bar{X}) \geq \frac{t}{N}] \leq \exp\left(-\frac{2t^2}{\sum_{i=1}^N (b_i - a_i)^2}\right) P[Xˉ−E(Xˉ)≥Nt]≤exp(−∑i=1N(bi−ai)22t2)
最后,为了得到形式与第二组不等式相同的表达式,让 t ′ = t N t' = \frac{t}{N} t′=Nt,则不等式变为:
P [ X ˉ − E ( X ˉ ) ≥ t ′ ] ≤ exp ( − 2 N 2 t ′ 2 ∑ i = 1 N ( b i − a i ) 2 ) P[\bar{X} - E(\bar{X}) \geq t'] \leq \exp\left(-\frac{2N^2t'^2}{\sum_{i=1}^N (b_i - a_i)^2}\right) P[Xˉ−E(Xˉ)≥t′]≤exp(−∑i=1N(bi−ai)22N2t′2)
这就得到了第二组不等式。现在,第二组不等式的形式与第一组不等式相同,只是将 t t t 替换为了 t ′ = t N t' = \frac{t}{N} t′=Nt,而其他部分保持不变。这个过程用到了线性变换的性质以及概率论的基本规则,允许我们从一个不等式推导到另一个不等式,只需简单的代换。
如何推理得到泛化误差上界
证明:
- 第一步
假设在每一个样本点 x i x_i xi, y i y_i yi处的损失为 X i , X i = L ( y i , f ( x i ) ) X_i,X_i=L(y_i,f(x_i)) Xi,Xi=L(yi,f(xi)),则
X ˉ = 1 N ∑ i = 1 N L ( y i , f ( x i ) ) = R ^ ( f ) \bar{X}=\frac{1}{N} \sum_{i=1}^NL(y_i,f(x_i))=\hat{R}(f) Xˉ=N1i=1∑NL(yi,f(xi))=R^(f)
E ( X ˉ ) = E ( 1 N ∑ i = 1 N L ( y i , f ( x i ) ) ) = 1 N ∑ i = 1 N E ( L ( y i , f ( x i ) ) ) = 1 N ∑ i = 1 N E ( L ( Y , f ( X ) ) ) = E ( L ( Y , F ( X ) ) ) = R ( f ) E(\bar{X})=E(\frac{1}{N} \sum_{i=1}^NL(y_i,f(x_i)))=\frac{1}{N} \sum_{i=1}^NE(L(y_i,f(x_i))) =\frac{1}{N} \sum_{i=1}^NE(L(Y,f(X)))=E(L(Y,F(X)))=R(f) E(Xˉ)=E(N1i=1∑NL(yi,f(xi)))=N1i=1∑NE(L(yi,f(xi)))=N1i=1∑NE(L(Y,f(X)))=E(L(Y,F(X)))=R(f)
对二分类问题,对于所有 i , [ a i , b i ] = [ 0 , 1 ] i,[a_i,b_i]=[0,1] i,[ai,bi]=[0,1]
这些等式是关于损失、经验风险和泛化误差的表达式,针对二分类问题,其中每个样本点都有一个损失函数 X i X_i Xi,损失函数的定义为 X i = L ( y i , f ( x i ) ) X_i = L(y_i, f(x_i)) Xi=L(yi,f(xi)),其中 y i y_i yi 是真实标签, f ( x i ) f(x_i) f(xi) 是模型 f f f 对输入 x i x_i xi 的预测。
以下是这些等式的解释:
-
X ˉ = 1 N ∑ i = 1 N L ( y i , f ( x i ) ) = R ^ ( f ) \bar{X}=\frac{1}{N} \sum_{i=1}^NL(y_i,f(x_i))=\hat{R}(f) Xˉ=N1∑i=1NL(yi,f(xi))=R^(f)
- X ˉ \bar{X} Xˉ 表示样本均值,也就是所有损失函数 X i X_i Xi 的平均值。
- R ^ ( f ) \hat{R}(f) R^(f) 表示经验风险,它是模型 f f f 在训练数据上的平均损失。
- 这个等式表示,样本均值 X ˉ \bar{X} Xˉ 等于模型 f f f 在训练数据上的经验风险 R ^ ( f ) \hat{R}(f) R^(f)。
-
E ( X ˉ ) = E ( 1 N ∑ i = 1 N L ( y i , f ( x i ) ) ) = 1 N ∑ i = 1 N E ( L ( y i , f ( x i ) ) ) = 1 N ∑ i = 1 N E ( L ( Y , f ( X ) ) ) = E ( L ( Y , F ( X ) ) ) = R ( f ) E(\bar{X})=E(\frac{1}{N} \sum_{i=1}^NL(y_i,f(x_i))) =\frac{1}{N} \sum_{i=1}^NE(L(y_i,f(x_i))) =\frac{1}{N} \sum_{i=1}^NE(L(Y,f(X)))=E(L(Y,F(X)))=R(f) E(Xˉ)=E(N1∑i=1NL(yi,f(xi)))=N1∑i=1NE(L(yi,f(xi)))=N1∑i=1NE(L(Y,f(X)))=E(L(Y,F(X)))=R(f)
- E ( X ˉ ) E(\bar{X}) E(Xˉ) 表示样本均值 X ˉ \bar{X} Xˉ 的期望值,即在所有可能的训练数据集上取平均得到的损失的期望值。
- E ( L ( y i , f ( x i ) ) ) E(L(y_i,f(x_i))) E(L(yi,f(xi))) 表示在单个样本点上的损失函数的期望值。
- 1 N ∑ i = 1 N E ( L ( y i , f ( x i ) ) ) \frac{1}{N} \sum_{i=1}^NE(L(y_i,f(x_i))) N1∑i=1NE(L(yi,f(xi))) 表示在整个训练数据集上的平均损失函数的期望值,也就是经验风险 R ^ ( f ) \hat{R}(f) R^(f) 的期望值。
- 1 N ∑ i = 1 N E ( L ( Y , f ( X ) ) ) \frac{1}{N} \sum_{i=1}^NE(L(Y,f(X))) N1∑i=1NE(L(Y,f(X))) 表示在所有可能的训练数据集上取平均得到的泛化误差的期望值。
- E ( L ( Y , F ( X ) ) ) E(L(Y,F(X))) E(L(Y,F(X))) 表示在所有可能的输入数据和真实标签上取平均得到的模型 f f f 的泛化误差的期望值。
- R ( f ) R(f) R(f) 表示模型 f f f 的泛化误差。
- 这个等式表示,样本均值 X ˉ \bar{X} Xˉ 的期望值等于模型 f f f 的泛化误差 R ( f ) R(f) R(f)。
总结起来,这些等式说明了在二分类问题中,经验风险 R ^ ( f ) \hat{R}(f) R^(f) 等于样本均值 X ˉ \bar{X} Xˉ,而模型 f f f 的泛化误差 R ( f ) R(f) R(f) 等于样本均值的期望值 E ( X ˉ ) E(\bar{X}) E(Xˉ)。这些等式强调了模型的经验风险和泛化误差之间的关系。
1 N ∑ i = 1 N E ( L ( y i , f ( x i ) ) ) = 1 N ∑ i = 1 N E ( L ( Y , f ( X ) ) ) \frac{1}{N} \sum_{i=1}^NE(L(y_i,f(x_i))) =\frac{1}{N} \sum_{i=1}^NE(L(Y,f(X))) N1∑i=1NE(L(yi,f(xi)))=N1∑i=1NE(L(Y,f(X)))
这两个表达式之所以相等,是因为它们表示了相同的概念,只是在符号上稍有不同。让我解释一下它们的含义:
-
1 N ∑ i = 1 N E ( L ( y i , f ( x i ) ) ) \frac{1}{N} \sum_{i=1}^N E(L(y_i, f(x_i))) N1∑i=1NE(L(yi,f(xi))):
- 这个表达式的意思是,首先对每个样本点 i i i 计算损失函数 L ( y i , f ( x i ) ) L(y_i, f(x_i)) L(yi,f(xi)) 的期望值,然后将这些期望值相加并取平均,其中 N N N 是样本数量。
- 损失函数 L ( y i , f ( x i ) ) L(y_i, f(x_i)) L(yi,f(xi)) 的期望值表示在给定输入 x i x_i xi 和真实标签 y i y_i yi 的情况下,模型 f f f 预测的损失的期望值。
-
1 N ∑ i = 1 N E ( L ( Y , f ( X ) ) ) \frac{1}{N} \sum_{i=1}^N E(L(Y, f(X))) N1∑i=1NE(L(Y,f(X))):
- 这个表达式的意思是,在所有可能的输入数据 X X X 和真实标签 Y Y Y 的情况下,首先计算模型 f f f 预测的损失函数 L ( Y , f ( X ) ) L(Y, f(X)) L(Y,f(X)) 的期望值,然后将这些期望值相加并取平均,其中 N N N 仍然表示样本数量。
- 这相当于对所有可能的训练数据集(每个训练数据集都有不同的 X X X 和 Y Y Y)计算模型的平均损失。
这两个表达式之所以相等,是因为它们都试图描述模型的平均损失,只是计算的方式略有不同。第一个表达式是在给定特定的训练数据集上计算平均损失,而第二个表达式是在考虑所有可能的训练数据集时计算平均损失。在实际应用中,通常只有一个训练数据集,因此第一个表达式更常见,但理论上它们等价。
X ˉ = 1 N ∑ i = 1 N L ( y i , f ( x i ) ) \bar{X}=\frac{1}{N} \sum_{i=1}^NL(y_i,f(x_i)) Xˉ=N1∑i=1NL(yi,f(xi))
这个等式是关于样本均值( X ˉ \bar{X} Xˉ)的定义,其中损失函数的期望值被表示为平均损失。让我解释一下这个等式是如何来的:
假设我们有一个包含 N N N 个样本的训练数据集,每个样本都由一个输入 x i x_i xi 和对应的真实标签 y i y_i yi 组成。我们使用模型 f f f 对每个输入 x i x_i xi 进行预测,并计算损失函数 L ( y i , f ( x i ) ) L(y_i, f(x_i)) L(yi,f(xi)) 的值。这个损失函数表示了模型对于每个样本的预测与真实标签之间的误差。
现在, 1 N ∑ i = 1 N L ( y i , f ( x i ) ) \frac{1}{N} \sum_{i=1}^N L(y_i, f(x_i)) N1∑i=1NL(yi,f(xi)) 表示的是计算了所有样本上的损失函数值,然后取了这些值的平均。这就是样本均值,表示了模型在整个训练数据集上的平均损失。
换句话说, X ˉ \bar{X} Xˉ 是模型 f f f 在训练数据集上的平均损失。这个等式的右侧表示对每个样本的损失函数 L ( y i , f ( x i ) ) L(y_i, f(x_i)) L(yi,f(xi)) 求期望值,然后将这些期望值相加并除以样本数量 N N N,这与计算平均损失的概念一致。
因此, X ˉ = 1 N ∑ i = 1 N L ( y i , f ( x i ) ) \bar{X} = \frac{1}{N} \sum_{i=1}^N L(y_i, f(x_i)) Xˉ=N1∑i=1NL(yi,f(xi)) 是样本均值的定义,它代表了模型在训练数据集上的平均损失。这个概念在机器学习中非常重要,因为我们经常希望了解模型在训练数据上的性能以及优化模型的损失函数。
- 第二步
推不下去了,等补补基础再来吧^_^
相关文章:

Hoeffing不等式
在李航老师的统计学习方法(第一版中) H o e f f i n g 不等式 Hoeffing不等式 Hoeffing不等式是这样子给出的 设 X 1 , X 2 , . . . , X N X_1,X_2,...,X_N X1,X2,...,XN是独立随机变量,且 X i ∈ [ a i , b i ] , i 1 , 2 , . . . ,…...

ffmpeg解复用指定pid转推udp
命令 ffmpeg -re -i udp://224.2.2.2:4003?fifo_size1024000 -map #5001 -acodec copy -flush_packets 1 -f mpegts udp://192.168.2.62:5161 ffmpeg -re -i udp://224.2.2.2:4003?fifo_size1024000 -map #5001 -acodec copy -flush_packets 1 -f mpegts udp://192.16…...
Vue组件通信方式
1.props通信 1.1在 Vue 2 中使用 props 通信 注意:props传递的数据是只读的,子组件修改,不会影响父组件 1.1.1.定义 props 在子组件中使用 props 选项来定义要接收的属性 // 子组件 <script> export default {props: {message: String} } </script>1.1.2.传递…...
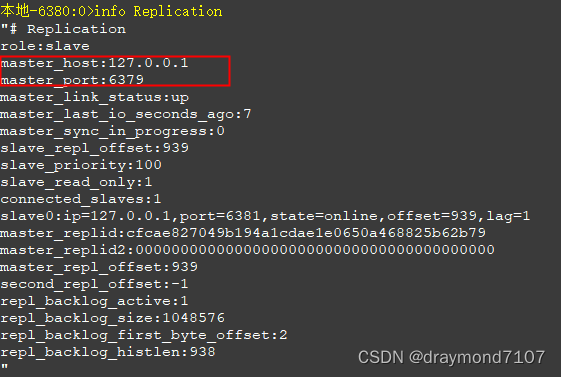
redis-设置从节点
节点结构 节点配置文件 主节点 不变 6380节点 port 6380 slaveof 127.0.0.1 63796381节点 port 6381 slaveof 127.0.0.1 6380启动 指定配置文件的方式启动 D:\jiqun\redis\Redis-6380>redis-server.exe redis.windows.conf启动时,会触发同步数据命令 主节点…...

k8s-实战——基于nfs实现动态存储
部署nfs服务 基于Centos7.9版本创建动态存储注意k8s版本应低于v1.24版本高k8s版本ServiceAccount需要手动创建secrets并关联相关sa部署流程 创建NFS共享服务、采用单独的节点用于nfs服务独占安装nfs-utils和rpcbindnfs客户端和服务端都安装nfs-utils包通过部署化脚本安装k8s集群…...

【广州华锐互动】鱼类授精繁殖VR虚拟仿真实训系统
随着科技的不断发展,虚拟现实技术在各个领域的应用越来越广泛。在养殖业中,VR技术可以帮助养殖户进行家鱼授精实操演练,提高养殖效率和繁殖成功率。本文将介绍利用VR开展家鱼授精实操演练的方法和应用。 首先,我们需要了解家鱼授精…...
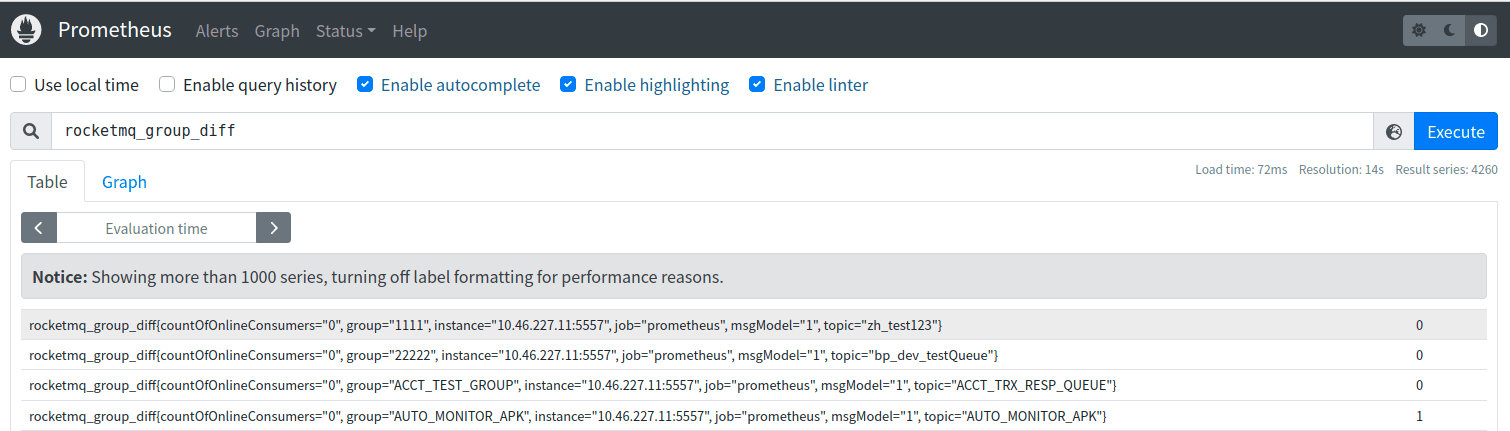
RocketMQ Promethus Exporter
介绍 Rocketmq-exporter 是用于监控 RocketMQ broker 端和客户端所有相关指标的系统,通过 mqAdmin 从 broker 端获取指标值后封装成 87 个 cache。 警告 过去版本曾是 87 个 concurrentHashMap,由于 Map 不会删除过期指标,所以一旦有 la…...

Kafka收发消息核心参数详解
文章目录 1、从基础的客户端说起1.1、消息发送者主流程1.2、消息消费者主流程 2、从客户端属性来梳理客户端工作机制2.1、消费者分组消费机制 1、从基础的客户端说起 Kafka提供了非常简单的客户端API。只需要引入一个Maven依赖即可: <dependency><groupId…...

Springboot中Aop的使用
Springboot中使用拦截器、过滤器、监听器-CSDN博客 相比较于拦截器,Spring 的aop则功能更强大,封装的更细致,需要单独引用 jar包。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-b…...

创建vue3项目、链式调用、setup函数、ref函数、reactive函数、计算和监听属性、vue3的生命周期、torefs的使用、vue3的setup写法
1 创建vue3项目 # 两种方式- vue-cli:vue脚手架---》创建vue项目---》构建vue项目--》工具链跟之前一样- vite :https://cn.vitejs.dev/-npm create vuelatest // 或者-npm create vitelatest一路选择即可# 运行vue3项目-vue-cli跟之前一样-vite 创建的…...

搭建好自己的PyPi服务器后怎么使用
当您成功搭建好自己的 PyPI 服务器后,您可以使用以下步骤来发布和使用您的包: 打包您的代码: 首先,将您的 Python 项目打包成一个发布包。确保您已经在项目根目录下创建了 setup.py 文件,并按照正确的格式填写了项目信…...

Vue3 中使用provide和reject
1、provide 和reject 可以实现一条事件线上的 父传子,父传孙等;相比较 props emits 仅限与父子传参更方便,相较于pinia书写更简单,但是需要注意使用响应式,如果是非响应式的会导致页面更新不及时 父组件 <templat…...
大数据flink篇之一-基础知识
一、起源 2010至2014年间,由柏林工业大学、柏林洪堡大学和哈索普拉特纳研究所联合发起名Stratosphere的研究项目。2014年4月,项目贡献给Apache基金会,成为孵化项目。更名为Flink2014年12月,成为基金会顶级项目2015年9月ÿ…...

No140.精选前端面试题,享受每天的挑战和学习
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云课上架的前后端实战课程《Vue.js 和 Egg.js 开发企业级健康管理项目》、《带你从入…...
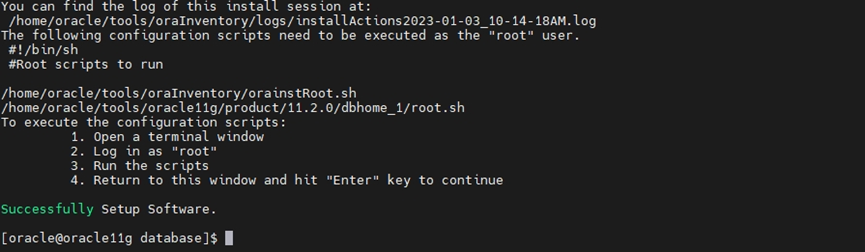
Oracle 11g_FusionOS_安装文档
同事让安装数据库,查询服务器信息发现操作系统是超聚变根据华为openEuler操作系统更改的自研操作系统,安装过程中踩坑不少,最后在超聚变厂商的技术支持下安装成功,步骤可参数该文。 一、 安装环境准备 1.1 软件下载 下载地址:…...
Linux驱动实现IO模型
在Linux系统分为内核态和用户态,CPU会在这两个状态之间进行切换。当进行IO操作时,应用程序会使用系统调用进入内核态,内核操作系统会准备好数据,把IO设备的数据加载到内核缓冲区。 然后内核操作系统会把内核缓冲区的数据从内核空…...

wsl2 更新报错问题解决记录
1、问题 win10 中安装的 wsl2,启动 docker desktop 时提示 wsl2 有问题: 于是点击推荐的地址连接到微软,下载 wsl2 的更新文件。之后运行,又报错: 更新被卡住。 2、解决方法 WinR 输入 cmd 打开命令行窗口&#x…...

突破算法迷宫:精选50道-算法刷题指南
前言 在计算机科学和编程领域,算法和数据结构是基础的概念,无论你是一名初学者还是有经验的开发者,都需要掌握它们。本文将带你深入了解一系列常见的算法和数据结构问题,包括二分查找、滑动窗口、链表、二叉树、TopK、设计题、动…...

玩转Mysql系列 - 第26篇:聊聊mysql如何实现分布式锁?
这是Mysql系列第26篇。 本篇我们使用mysql实现一个分布式锁。 分布式锁的功能 分布式锁使用者位于不同的机器中,锁获取成功之后,才可以对共享资源进行操作 锁具有重入的功能:即一个使用者可以多次获取某个锁 获取锁有超时的功能ÿ…...

linux 解压缩命令tar
Tar tar 命令的选项有很多(用 man tar 可以查看到),但常用的就那么几个选项,下面来举例说明一下: tar -cf all.tar *.jpg 这条命令是将所有.jpg 的文件打成一个名为 all.tar 的包。-c 是表示产生新的包,-f 指 定包的文件名。 …...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...
