用Java打印长方形、平行四边形 、三角形、菱形、空心菱形
今天复习使用嵌套for来完成一些任务,于是想着打印一些图形来练习

思考感悟
长方形
行数 和 每行的星星数嵌套遍历即可
平行四边形
核心:每行空格数=总行数-行数
| 行数 | 空格数 |
|---|---|
| 1 | 3 |
| 2 | 2 |
| 3 | 1 |
三角形
核心:每行星星数=2*当前行数-1
| 行数 | 星星数 |
|---|---|
| 1 | 1 |
| 2 | 3 |
| 3 | 5 |
| 4 | 7 |
菱形
核心:每行空格数=行数
| 行数 | 空格数 |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
核心:每行星星数=7-2*当前行数
| 行数 | 星星数 |
|---|---|
| 1 | 5 |
| 2 | 3 |
| 3 | 1 |
空心菱形
核心:首尾有星星
# 代码提供
public class HelloWorld{public static void main(String[] args){//长方形//s1();//增加边框//s2();//平行四边形//s3();//三角形//s4();//菱形//s5();//空心菱形s6();}static void s1(){for(int b=1;b<=4;b++){System.out.println();for(int a=1;a<=7;a++){System.out.print("*");} } }static void s2(){for(int b=1;b<=4;b++){System.out.println();for(int c=1;c<=5;c++){System.out.print(" ");}for(int a=1;a<=7;a++){System.out.print("*");} } }static void s3(){for(int b=1;b<=4;b++){System.out.println();for(int c=1;c<=5;c++){System.out.print(" ");}for(int d=1;d<=4-b;d++){System.out.print(" ");}for(int a=1;a<=7;a++){System.out.print("*");} } }static void s4(){for(int b=1;b<=4;b++){System.out.println();for(int c=1;c<=5;c++){System.out.print(" ");}for(int d=1;d<=4-b;d++){System.out.print(" ");}for(int a=1;a<=b*2-1;a++){System.out.print("*");} } }static void s5(){for(int b=1;b<=4;b++){System.out.println();for(int c=1;c<=5;c++){System.out.print(" ");}for(int d=1;d<=4-b;d++){System.out.print(" ");}for(int a=1;a<=b*2-1;a++){System.out.print("*");} }for(int b=1;b<=3;b++){System.out.println();for(int c=1;c<=5;c++){System.out.print(" ");}for(int d=1;d<=b;d++){System.out.print(" ");} for(int a=1;a<=7-2*b;a++){System.out.print("*");} }}static void s6(){for(int b=1;b<=4;b++){System.out.println();for(int c=1;c<=5;c++){System.out.print(" ");}for(int d=1;d<=4-b;d++){System.out.print(" ");}for(int a=1;a<=b*2-1;a++){if(a==1 || a==b*2-1){System.out.print("*"); }else{System.out.print(" "); }} }for(int b=1;b<=3;b++){System.out.println();for(int c=1;c<=5;c++){System.out.print(" ");}for(int d=1;d<=b;d++){System.out.print(" ");} for(int a=1;a<=7-2*b;a++){if(a==1 || a==7-2*b){System.out.print("*"); }else{System.out.print(" "); }} }}
}
相关文章:

用Java打印长方形、平行四边形 、三角形、菱形、空心菱形
今天复习使用嵌套for来完成一些任务,于是想着打印一些图形来练习 思考感悟 长方形 行数 和 每行的星星数嵌套遍历即可 平行四边形 核心:每行空格数总行数-行数 行数空格数132231 三角形 核心:每行星星数2*当前行数-1 行数星星数1123…...

es6模块化,怎么判断当前文件使用的是es6的模块化还是commenjs的模块化
es6的模块化,文件中的this,指向undefined,不是指向window import.meta - JavaScript | MDN...
Ubuntu 基础配置
源配置 源路径: /etc/apt/sources.list aliyun源 20.04 deb http://mirrors.aliyun.com/ubuntu/ focal main restricted universe multiverse deb http://mirrors.aliyun.com/ubuntu/ focal-security main restricted universe multiverse deb http://mirrors.a…...

CISSP学习笔记:人员安全和风险管理概念
第二章 人员安全和风险管理概念 2.1 促进人员安全策略 职责分离: 把关键的、重要的和敏感工作任务分配给若干不同的管理员或高级执行者,防止共谋工作职责:最小特权原则岗位轮换:提供知识冗余,减少伪造、数据更改、偷窃、阴谋破坏和信息滥用的风险&…...
ubuntu18.04 OpenGL开发(显示YUV)
源码参考:https://download.csdn.net/download/weixin_55163060/88382816 安装opengl库 sudo apt install libglu1-mesa-dev freeglut3-dev mesa-common-dev 安装opengl工具包 sudo apt install mesa-utils 检查opengl版本信息(桌面终端执行)…...

React(react18)中组件通信06——redux-toolkit + react-redux
React(react18)中组件通信06——redux-toolkit react-redux 1 前言1.1 redux 和 react-redux1.2 关于redux-toolkit1.2.1 官网1.2.2 为什么要用Redux Toolkit? 1.3 安装 Redux Toolkit1.4 Redux Toolkit相关API 2. 开始例子——官网例子2.1 …...
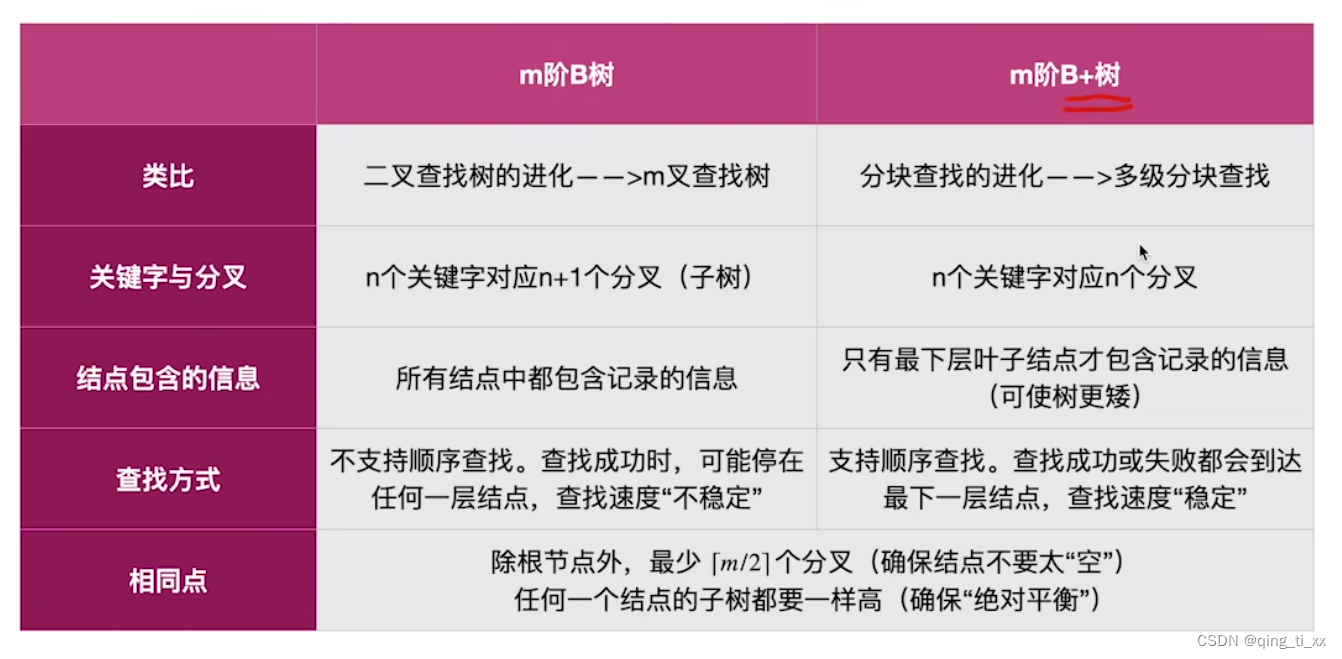
第七章 查找 九、B+树
目录 一、定义 二、B树需要满足的条件 三、重要考点 一、定义 1、B树是一种常用的数据结构,用于实现关系型数据库中的索引。 2、其特点是可以在磁盘等外存储器上高效地存储大量数据,并支持快速的查询、插入、删除等操作。 3、B树的结构类似于二叉搜…...
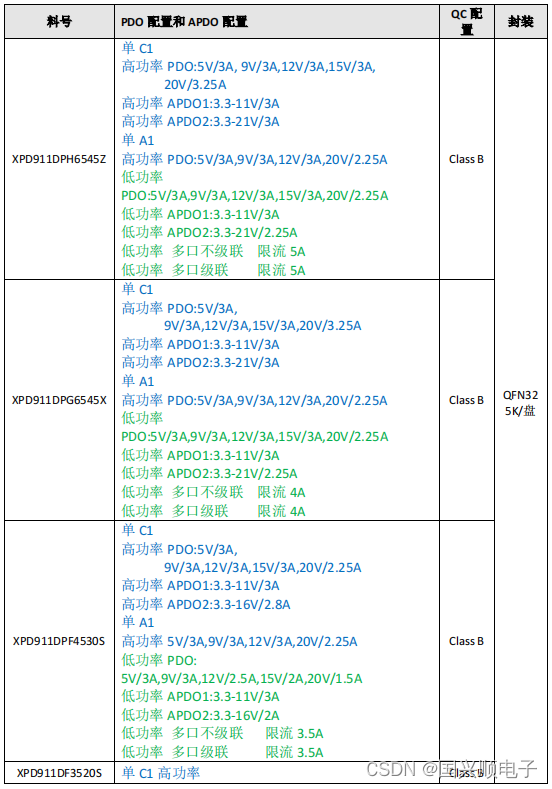
XPD911协议系列-集成同步降压多口互联控制器
产品描述: XPD911 是一款集成 USB Type-C、USB Power Delivery(PD) 3.1 以及 PPS、 QC3.0/3.0 /2.0 快充协议、华为 FCP/SCP/HVSCP 快充协议、三星 AFC 快充协议、VOOC 快充协议、MTK PE 快充协议、BC1.2 DCP 以及苹果设备 2.4A 充电规范的多…...
)
数字反转(蓝桥杯)
数字反转 题目描述 给定一个整数,请将该数各个位上数字反转得到一个新数。新数也应满足整数的常见形式,即除非给定的原数为零,否则反转后得到的新数的最高位数字不应为零(参见实例 2)。 输入描述 输入共 1 行&…...
)
十一.EtherCAT开发之microchip MCU D51+ LAN9253 的开发FOE应用(SPI directly 模式)
十一.EtherCAT开发之microchip MCU D51+ LAN9253 的开发FOE应用(SPI directly 模式) 文章目录 十一.EtherCAT开发之microchip MCU D51+ LAN9253 的开发FOE应用(SPI directly 模式)11.0 软件更新方式11.1 SSC TOOL配置11.2 MCU D51 FOE函数支持11.2.1 下载download11.2.2 上传up…...
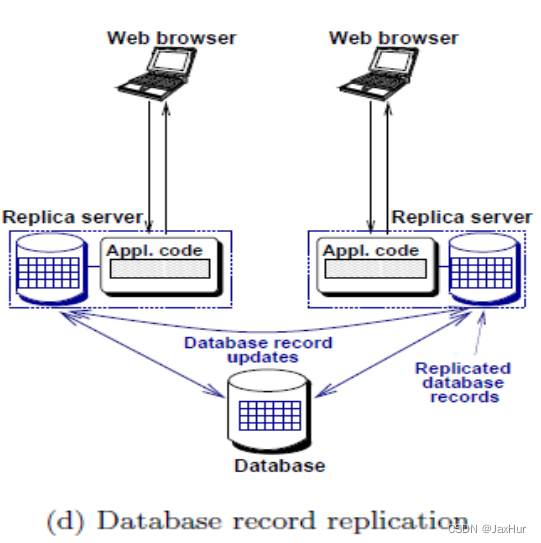
【分布式计算】二、架构(Architectures)
1.中心化架构(Centralized Architectures) 1.1.经典C/S模型 服务器:一个或多个进程提供服务 客户端:一个或多个进程使用服务 客户端和服务器可以在不同的机器上 客户端遵循请求/回复模型 1.2.传统三层视图 用户界面层&#x…...
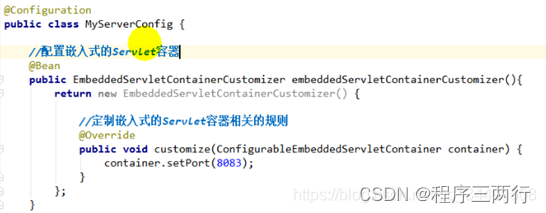
Springboot对MVC、tomcat扩展配置
Springboot在web层的开发基本都是采用Springmvc框架技术,但是Springmvc中的某些配置在boot是没有的,我们就应该根据自己的需求进行对mvc扩展配置 Springboot1.x版本如何配置 通过注解Configuration一个类,继承webmvcconfigureradapter&#…...
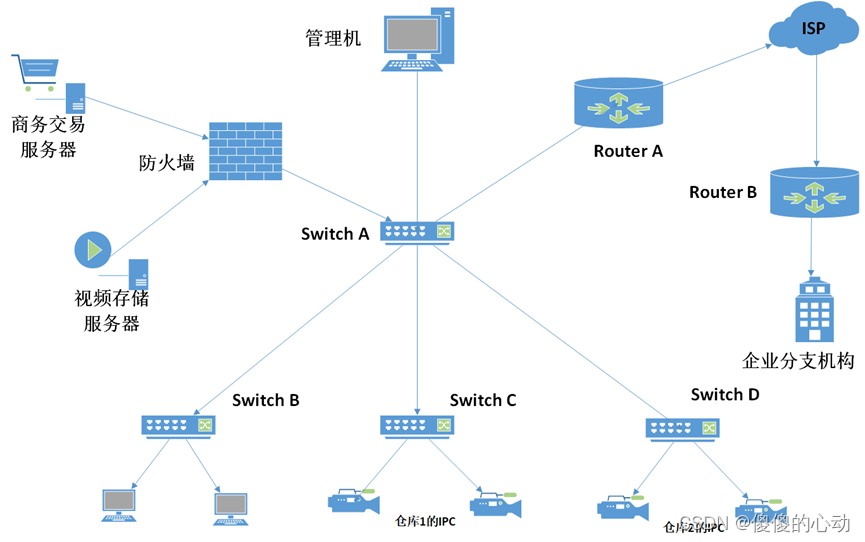
网络子网划分练习
网络子网划分练习 1.背景: 在一个仓储企业网络拓朴结构如图1-所示,该企业占地500亩。有五层办公楼1栋,大型仓库10栋。每栋仓库内、外部配置视频监控16台,共计安装视频监控160台,Switch A、服务器、防火墙、管理机、Rou…...

Leetcode刷题笔记--Hot51-60
1--环形链表II 主要思路: 快慢指针,快指针每次走两步,慢指针每次走一步; 第一次相遇时,假设慢指针共走了 f 步,则快指针走了 2f 步; 假设起点到环入口结点的长度为 a(不包括入口结点…...
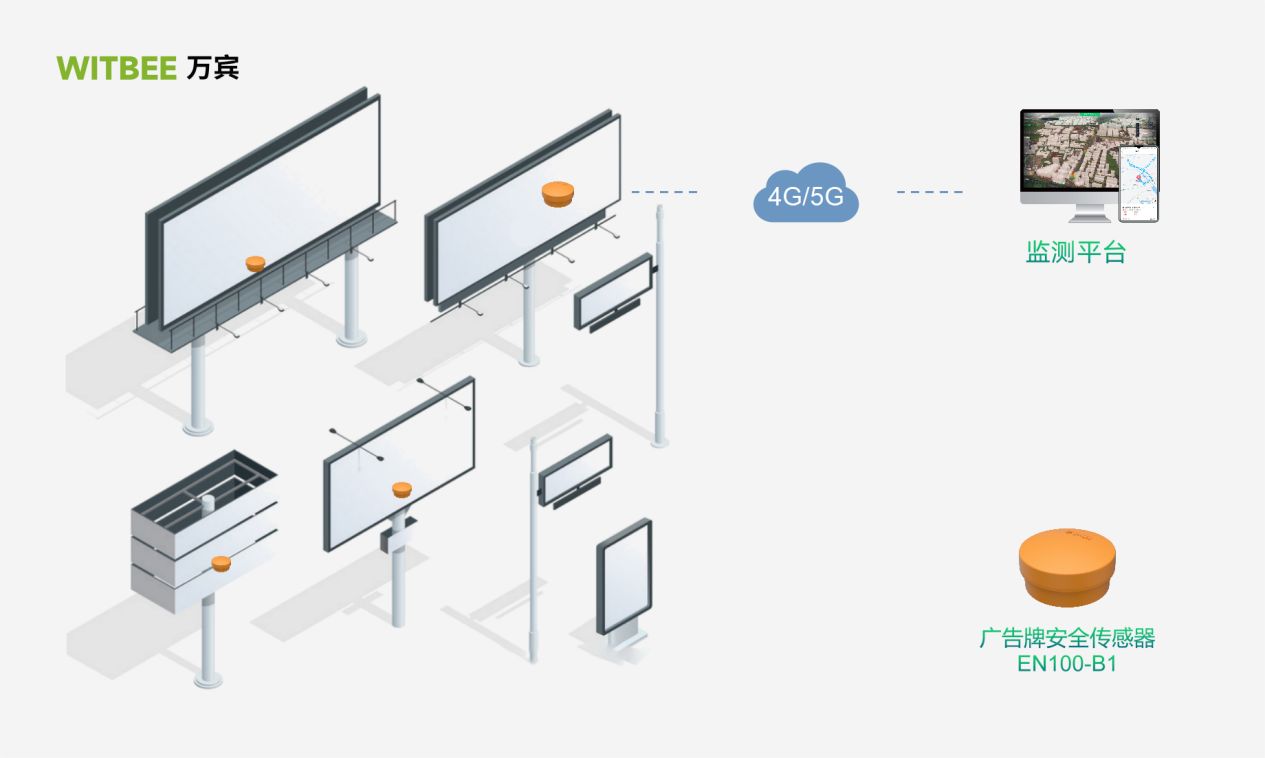
广告牌安全监测系统,用科技护航大型广告牌安全
城市的街头巷尾,处处可见高耸的广告牌,它们以各种形式和颜色吸引着行人的目光。然而,作为城市景观的一部分,广告牌的安全性常常被我们所忽视。广告牌量大面大,由于设计、材料、施工方法的缺陷,加上后期的检…...

volatile
什么是volatile volatile是Java提供的一种轻量级的同步机制。Java 语言包含两种内在的同步机制:同步块(或方法)和 volatile 变量,相比于synchronized(synchronized通常称为重量级锁),volatile更…...
JAVA:实现Excel和PDF上下标
1、简介 最近项目需要实现26个小写字母的上下标功能,自己去网上找了所有Unicode的上下标形式,缺少一些关键字母,顾后面考虑自己创建上下标字体样式,以此来记录。 2、Excel Excel本身是支持上下标,我们可以通过Excel单元格的样式来设置当前字体上下标,因使用的是POI的m…...

AI写稿软件,最新的AI写稿软件有哪些
写作已经成为各行各业无法绕开的重要环节。不论是企业的广告宣传、新闻媒体的报道、还是个人自媒体的内容创作,文字都扮演着不可或缺的角色。随着信息的爆炸式增长,写作的需求也不断攀升,这使得许多人感到困扰。时间不够用、创意枯竭、写作技…...
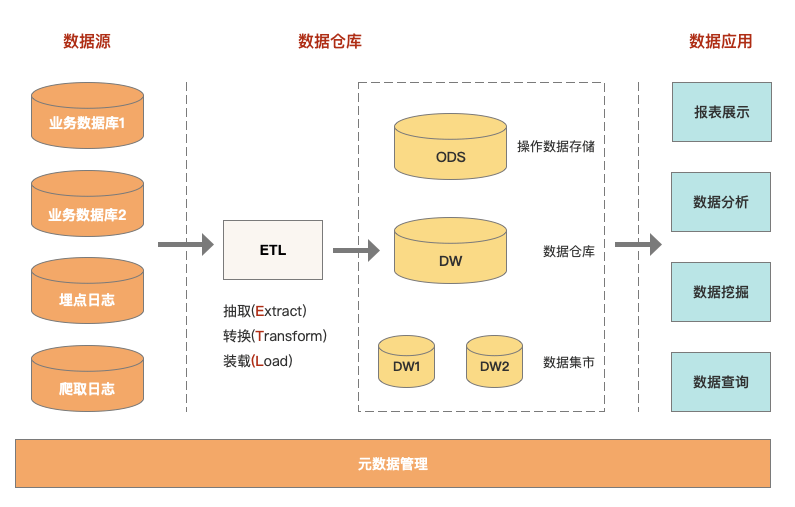
干货:数据仓库基础知识(全)
1、什么是数据仓库? 权威定义:数据仓库是一个面向主题的、集成的、相对稳定的、反映历史变化的数据集合,用于支持管理决策。 1)数据仓库是用于支持决策、面向分析型数据处理; 2)对多个异构的数据源有效集…...

二分搜索简介
概念: 二分搜索算法(Binary Search)是一种高效的搜索算法,用于在有序数组中查找特定元素的位置。它的基本思想是将数组分为两部分,通过比较目标值与数组中间元素的大小关系,确定目标值可能存在的区间&…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...
