学习笔记——BSGS
众所周知,北上广深是中国非常一线的城市,北京是首都,地处……
正片开始!
一、BSGS基础算法
实现目标: A x ≡ B ( m o d P ) , ( gcd ( P , A ) = 1 ) A^x\equiv B(\mod P),(\gcd(P,A)=1) Ax≡B(modP),(gcd(P,A)=1)求最小的 x x x
很明显,如果暴力枚举,时间是 O ( P ) O(P) O(P)的,只要题目数据范围大,就死定了。愿意的人欢迎尝试(无100警告)
于是,考虑 ~ 莫队
~~~~~~~~~~~~~~~~ 分块
~~~~~~~~~~~~~~~~ BSGS
为什么我要提前两个?
因为BSGS本质就是分块!
简单讲解一下,就是将本来 P P P种情况,平均分成了$\sqrt p $份,对每份内进行预处理
不直观?好,那就用直观的式子吧!
令 x = k p − t \texttt{令}x=k\sqrt p-t 令x=kp−t
即 A k p ≡ A t B ( m o d p ) \texttt{即}A^{k\sqrt p}\equiv A^tB (\mod p) 即Akp≡AtB(modp)
于是,找个哈希表维护一下后面的即可
IO::pin>>y>>z>>p;
gp_hash_table<int,int> ht;
int f,s;
bool flg;
ht.clear();
f=ceil(sqrt(p));
s=1;
flg=1;
for(int i=1; i<=f; i++)s=1ll*s*y%p,ht[1ll*z*s%p]=i;
for(int j=1,k=s; j<=f; j++) {if(ht[k]&&flg) {wt(((1ll*j*f-ht[k])%p+p)%p,'\n');flg=0;}k=(1ll*s*k)%p;}if(flg)puts("Orz, I cannot find x!");
附赠模板代码
#pragma GCC optimize(1,"inline","Ofast")
#pragma GCC optimize(2,"inline","Ofast")
#pragma GCC optimize(3,"inline","Ofast")
#include<bits/stdc++.h>
#include<bits/extc++.h>
using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
namespace IO {class input {private:bool isdigit(char c) {return ('0'<=c&&c<='9');}public:input operator>>(int &x) {x=0;bool y=1;char c=getchar();while(!isdigit(c))y&=(c!='-'),c=getchar();while(isdigit(c))x=(x<<1)+(x<<3)+(c^48),c=getchar();if(!y)x=-x;return *this;}input operator>>(short &x) {x=0;bool y=1;char c=getchar();while(!isdigit(c))y&=(c!='-'),c=getchar();while(isdigit(c))x=(x<<1)+(x<<3)+(c^48),c=getchar();if(!y)x=-x;return *this;}input operator>>(bool &x) {x=0;bool y=1;char c=getchar();while(!isdigit(c))y&=(c!='-'),c=getchar();while(isdigit(c))x=(x<<1)+(x<<3)+(c^48),c=getchar();if(!y)x=-x;return *this;}input operator>>(long &x) {x=0;bool y=1;char c=getchar();while(!isdigit(c))y&=(c!='-'),c=getchar();while(isdigit(c))x=(x<<1)+(x<<3)+(c^48),c=getchar();if(!y)x=-x;return *this;}input operator>>(long long &x) {x=0;bool y=1;char c=getchar();while(!isdigit(c))y&=(c!='-'),c=getchar();while(isdigit(c))x=(x<<1)+(x<<3)+(c^48),c=getchar();if(!y)x=-x;return *this;}input operator>>(__int128 &x) {x=0;bool y=1;char c=getchar();while(!isdigit(c))y&=(c!='-'),c=getchar();while(isdigit(c))x=(x<<1)+(x<<3)+(c^48),c=getchar();if(!y)x=-x;return *this;}input operator>>(unsigned int &x) {x=0;bool y=1;char c=getchar();while(!isdigit(c))y&=(c!='-'),c=getchar();while(isdigit(c))x=(x<<1)+(x<<3)+(c^48),c=getchar();if(!y)x=-x;return *this;}input operator>>(unsigned short &x) {x=0;bool y=1;char c=getchar();while(!isdigit(c))y&=(c!='-'),c=getchar();while(isdigit(c))x=(x<<1)+(x<<3)+(c^48),c=getchar();if(!y)x=-x;return *this;}input operator>>(unsigned long &x) {x=0;bool y=1;char c=getchar();while(!isdigit(c))y&=(c!='-'),c=getchar();while(isdigit(c))x=(x<<1)+(x<<3)+(c^48),c=getchar();if(!y)x=-x;return *this;}input operator>>(unsigned long long &x) {x=0;bool y=1;char c=getchar();while(!isdigit(c))y&=(c!='-'),c=getchar();while(isdigit(c))x=(x<<1)+(x<<3)+(c^48),c=getchar();if(!y)x=-x;return *this;}input operator>>(unsigned __int128 &x) {x=0;bool y=1;char c=getchar();while(!isdigit(c))y&=(c!='-'),c=getchar();while(isdigit(c))x=(x<<1)+(x<<3)+(c^48),c=getchar();if(!y)x=-x;return *this;}input operator>>(double &x) {x=0;bool y=1;char c=getchar();while(!isdigit(c))y&=(c!='-'),c=getchar();while(isdigit(c))x=x*10+(c^48),c=getchar();if(!y)x=-x;if(!isdigit(c))if(c!='.')return *this;double z=1;while(isdigit(c))z/=10.,x=x+z*(c^48),getchar();return *this;}input operator>>(long double &x) {x=0;bool y=1;char c=getchar();while(!isdigit(c))y&=(c!='-'),c=getchar();while(isdigit(c))x=x*10+(c^48),c=getchar();if(!y)x=-x;if(!isdigit(c))if(c!='.')return *this;double z=1;while(isdigit(c))z/=10.,x=x+z*(c^48),c=getchar();return *this;}input operator>>(float &x) {x=0;bool y=1;char c=getchar();while(!isdigit(c))y&=(c!='-'),c=getchar();while(isdigit(c))x=x*10+(c^48),c=getchar();if(!y)x=-x;if(!isdigit(c))if(c!='.')return *this;double z=1;while(isdigit(c))z/=10.,x=x+z*(c^48),c=getchar();return *this;}input operator>>(std::string &x) {char c=getchar();x.clear();while(!(c!=' '&&c!='\n'&&c!=' '&&c!=EOF&&c))c=getchar();while(c!=' '&&c!='\n'&&c!=' '&&c!=EOF&&c) {x.push_back(c);c=getchar();}return *this;}input operator>>(char *x) {char c=getchar();int cnt=0;while(!(c!=' '&&c!='\n'&&c!=' '&&c!=EOF&&c))c=getchar();while(c!=' '&&c!='\n'&&c!=' '&&c!=EOF&&c) {x[cnt++]=c;c=getchar();}return *this;}input operator>>(char x) {x=getchar();return *this;}} pin;
};
inline void wt(char ch) {putchar(ch);
}
template<class T>
inline void wt(T x) {static char ch[40];int p=0;if(x<0)putchar('-'),x=-x;doch[++p]=(x%10)^48,x/=10;while(x);while(p)putchar(ch[p--]);
}
template<class T,class... U>
inline void wt(T x,U ...t) {wt(x),wt(t...);
}
#define int long long
#define rep(i,a,b) for(int i=a,i##end=b;i<=i##end;i++)
#define frep(i,a,b) for(int i=a,i##end=b;i>=i##end;i--)
#define lqrep(i,a,v) for(int i=hd[a],v=e[i].v;i>=i##end;i=e[i].nxt,v=e[i].v)
const int N=1e5+7;
main() {
}
//目前快速输出pout还未搞定哦
到此就结束了吗?
当然不是!!!!!!!!!!
如果没有 gcd ( P , A ) = 1 \gcd(P,A)=1 gcd(P,A)=1的话,前面的一切都成了一纸空文
那该如何?
如果不需要的旅客们可以摆烂了,以下是扩展板
二、BSGS基础算法
不妨设 gcd ( P , A ) = d \gcd(P,A)=d gcd(P,A)=d
A x ≡ B ( m o d P ) − > ( A ′ × d ) x ≡ B ′ × d ( m o d P ) − > ( A ′ × d ) x − 1 ≡ B ′ ∗ A ′ − 1 ( m o d P ) A^x\equiv B(\mod P)->\\(A'\times d)^x\equiv B'\times d(\mod P)->\\(A'\times d)^{x-1}\equiv B'*A'^{-1}(\mod P) Ax≡B(modP)−>(A′×d)x≡B′×d(modP)−>(A′×d)x−1≡B′∗A′−1(modP)
接着按上文求解即可
相关文章:

学习笔记——BSGS
众所周知,北上广深是中国非常一线的城市,北京是首都,地处…… 正片开始! 一、BSGS基础算法 实现目标: A x ≡ B ( m o d P ) , ( gcd ( P , A ) 1 ) A^x\equiv B(\mod P),(\gcd(P,A)1) Ax≡B(modP),(gcd(P,A)1)…...

【AI视野·今日NLP 自然语言处理论文速览 第四十期】Mon, 25 Sep 2023
AI视野今日CS.NLP 自然语言处理论文速览 Mon, 25 Sep 2023 Totally 46 papers 👉上期速览✈更多精彩请移步主页 Daily Computation and Language Papers ReConcile: Round-Table Conference Improves Reasoning via Consensus among Diverse LLMs Authors Justin C…...
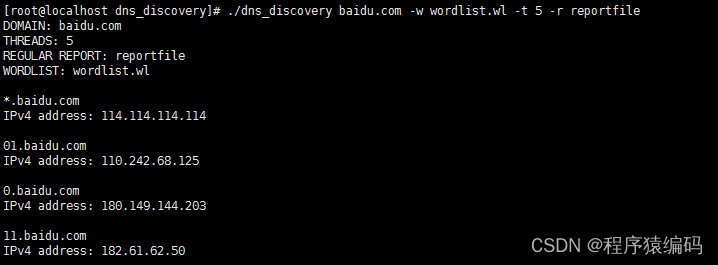
Linux C/C++下收集指定域名的子域名信息(类似dnsmap实现)
我们知道dnsmap是一个工具,主要用于收集指定域名的子域名信息。它对于渗透测试人员在基础结构安全评估的信息收集和枚举阶段非常有用,可以帮助他们发现目标公司的IP网络地址段、域名等信息。 dnsmap的操作原理 dnsmap(DNS Mappingÿ…...
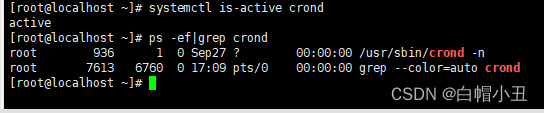
linux-定时任务
目录 一、crond命令 1、什么是计划任务 2、crond服务的概念 3、crontab 二、at命令 1、at任务的概念 三、邮件服务 1、概念 2、启动postfix 四、mailx命令 1、三个概念: 2、交互式发邮件 3、非交互式发邮件 四、cron定时任务实践 1、系统定时任务配置…...

在Spring Boot项目中使用Redisson
在Spring Boot项目中使用Redisson Redisson简介 Redisson官网仓库 Redisson中文文档 Redission是一个基于Java的分布式缓存和分布式任务调度框架,用于处理分布式系统中的缓存和任务队列。它是一个开源项目,旨在简化分布式系统的开发和管理。 以下是…...
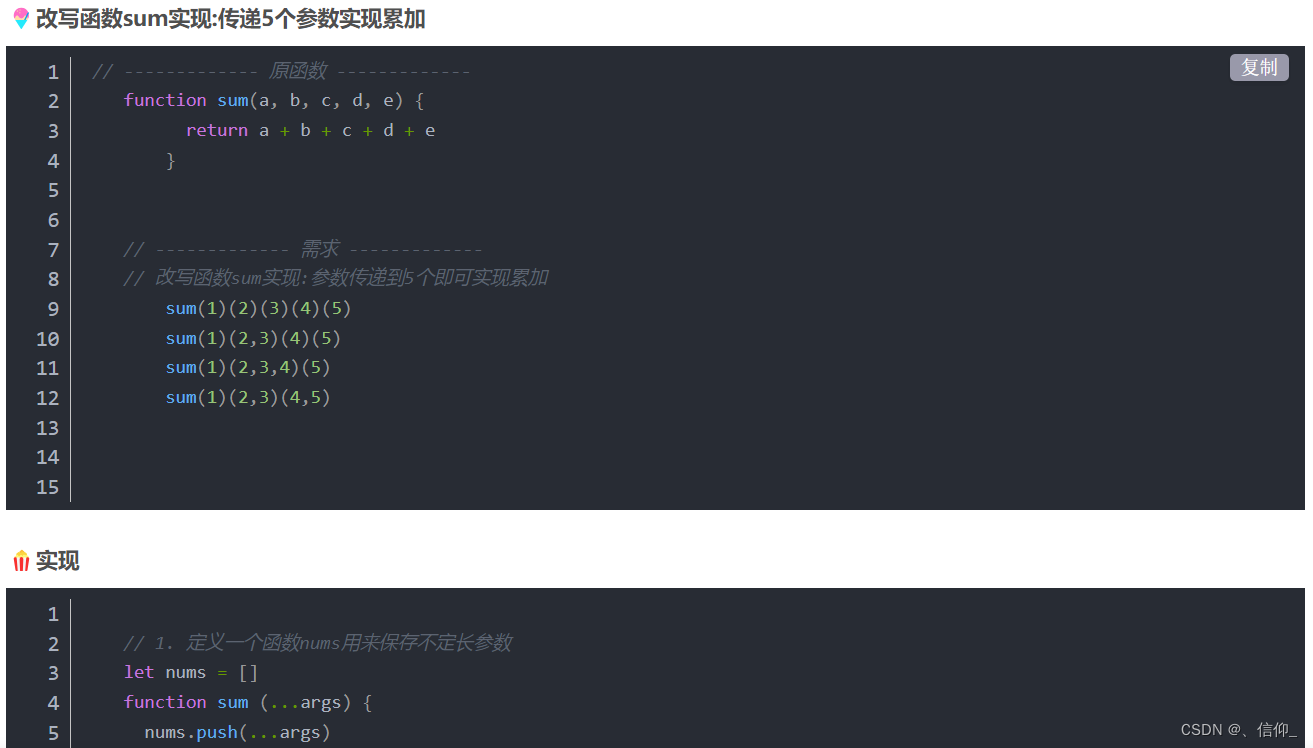
JavaScript 函数柯里化
🎶什么是柯里化 柯里化(Currying)是把接受多个参数的函数变换成接受一个单一参数(最初函数的第一个参数)的函数,并且返回接受余下的参数且返回结果的新函数的技术。 🎡简单的函数柯里化的实现 // ------------- 原函数…...
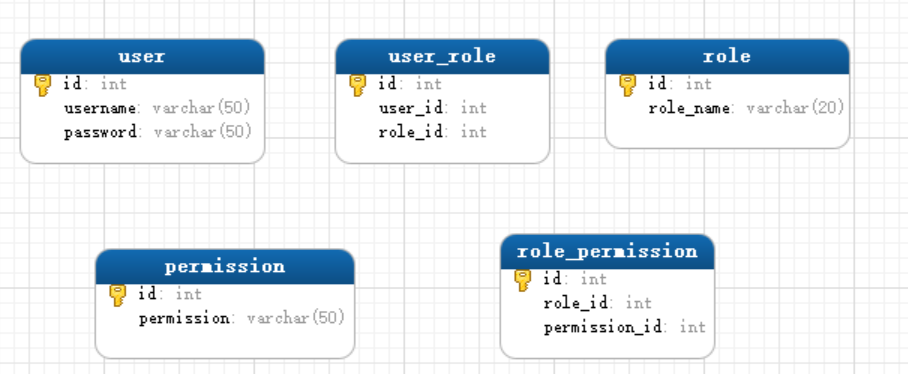
springboot实现ACL+RBAC权限体系
本文基于web系统的权限控制非常重要的前提下,从ALC和RBAC权限控制两个方面,介绍如何在springboot项目中实现一个完整的权限体系。 源码下载 :https://gitee.com/skyblue0678/springboot-demo 序章 一个后台管理系统,基本都有一套…...

C++20协程示例
C20协程示例 认识协程 在C中,协程就是一个可以暂停和恢复的函数。 包含co_wait、co_yield、co_return关键字的都可以叫协程。 看一个例子: MyCoroGenerator<int> testFunc(int n) {std::cout << "Begin testFunc" << s…...
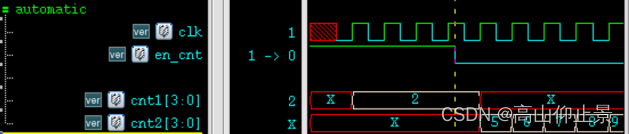
【Verilog 教程】6.2Verilog任务
关键词:任务 任务与函数的区别 和函数一样,任务(task)可以用来描述共同的代码段,并在模块内任意位置被调用,让代码更加的直观易读。函数一般用于组合逻辑的各种转换和计算,而任务更像一个过程&a…...
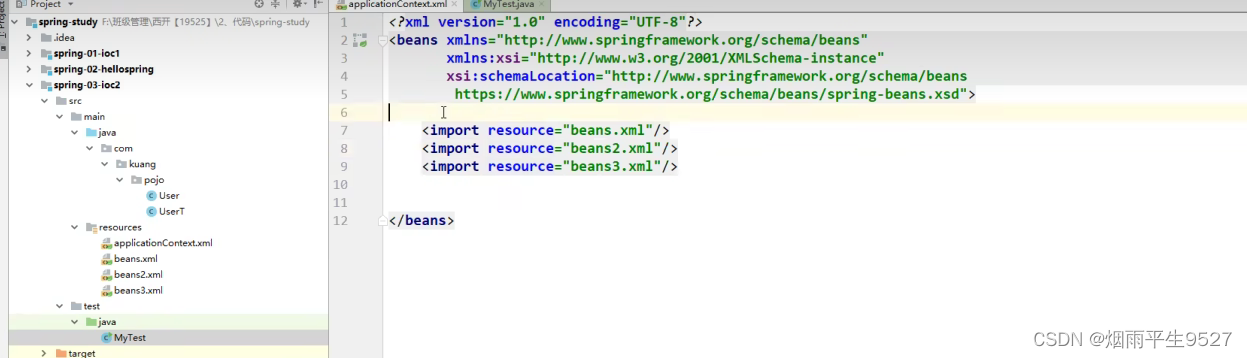
Spring修炼之路(1)基础入门
一、简介 1.1Spring概述 Spring框架是一个轻量级的Java开发框架,它提供了一系列底层容器和基础设施,并可以和大量常用的开源框架无缝集成,可以说是开发Java EE应用程序的必备。Spring是一个轻量级的控制反转(IoC)和面向切面(AOP)的容器&…...

GANs学习记录
GAN 基于GAN的研究识别相关不同背景目标图像 可以用Augmentation2021.3.15 基于GAN的研究 是通过GAN 进行图像重建,恢复细节,去模糊,提高图像质量,图像还原,去噪等等。 识别相关 一种基于生成对抗网络的训练样本扩充…...

Flink-CDC——MySQL、SqlSqlServer、Oracle、达梦等数据库开启日志方法
目录 1. 前言 2. 数据源安装与配置 2.1 MySQL 2.1.1 安装 2.1.2 CDC 配置 2.2 Postgresql 2.2.1 安装 2.2.2 CDC 配置 2.3 Oracle 2.3.1 安装 2.3.2 CDC 配置 2.4 SQLServer 2.4.1 安装 2.4.2 CDC 配置 2.5达梦 2.4.1安装 2.4.2CDC配置 3. 验证 3.1 Flink版…...

linux设置tomcat redis开机自启动
设置Tomcat自启动 1.修改 /etc/rc.d/rc.local 文件 [rootiowZ]# vim /etc/rc.d/rc.local在/etc/rc.d/rc.local文件最后加上: export JAVA_HOME/usr/local/jdk /usr/local/apache-tomcat-8.5.73/bin/startup.sh start退出vim并保存修改的文件。 说明:/u…...

跨域问题讨论
问题 跨域定义 当一个请求url的协议、域名、端口三者之间任意一个与当前页面地址不同即为跨域。 跨域的安全隐患(CSRF攻击) 也就是说,一旦允许跨域,意味着允许恶意网站随意攻击可信网站,带来安全风险。 这里面有一…...

ESP32设备通信-两个ESP32设备之间HTTP通信
两个ESP32设备之间HTTP通信 文章目录 两个ESP32设备之间HTTP通信1、应用介绍2、软件准备3、硬件准备4、代码实现4.1 ESP32服务器节点代码4.2 ESP32客户端节点代码在本文中,我们将介绍如何在没有任何物理路由器或互联网连接的情况下使用 Wi-Fi 在两个 ESP32 开发板之间执行无线…...
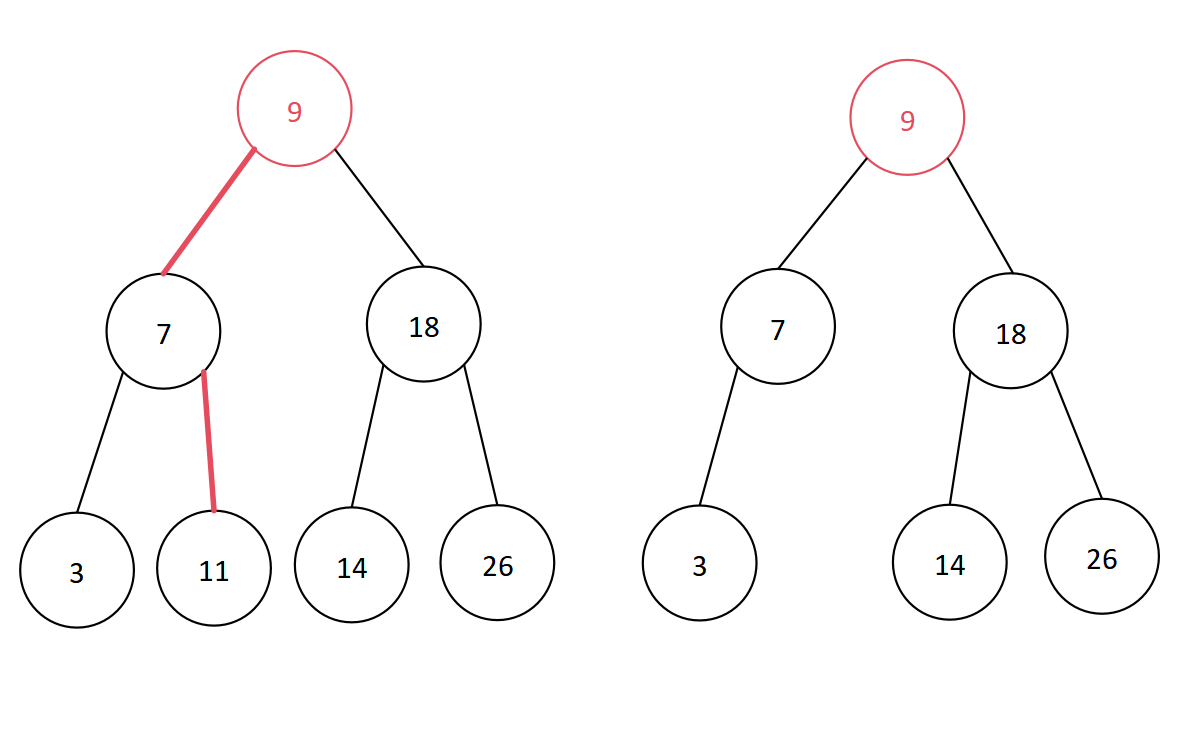
数据结构学习笔记——查找算法中的树形查找(平衡二叉树)
目录 一、平衡二叉树的定义二、平衡因子三、平衡二叉树的插入和构造(一)LL型旋转(二)LR型旋转(三)RR型旋转(四)RL型旋转 四、平衡二叉树的删除(一)叶子结点&a…...

P1830 轰炸III
题目背景 一个大小为 ��nm 的城市遭到了 �x 次轰炸,每次都炸了一个每条边都与边界平行的矩形。 题目描述 在轰炸后,有 �y 个关键点,指挥官想知道,它们有没有受到过轰炸,如…...

大语言模型LLM知多少?
你知道哪些流行的大语言模型?你都体验过哪写? GPT-4,Llamma2, T5, BERT 还是 BART? 1.GPT-4 1.1.GPT-4 模型介绍 GPT-4(Generative Pre-trained Transformer 4)是由OpenAI开发的一种大型语言模型。GPT-4是前作GPT系列模型的进一步改进,旨在提高语言理解和生成的能力,…...

Redis命令行使用Lua脚本
Redis命令行使用Lua脚本 Lua脚本在Redis中的使用非常有用,它允许你在Redis服务器上执行自定义脚本,可以用于复杂的数据处理、原子性操作和执行多个Redis命令。以下是Lua脚本在Redis中的基本使用详细讲解: 运行Lua脚本: 在Redis中…...

HTML详细基础(三)表单控件
本帖介绍web开发中非常核心的标签——表格标签。 在日常我们使用到的各种需要输入用户信息的场景——如下图,均是通过表格标签table创造出来的: 目录 一.表格标签 二.表格属性 三.合并单元格 四.无序列表 五.有序列表 六.自定义标签 七.表单域 …...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...
